“做数学”对初中生数学核心素养表现影响的实验研究

许天枢，赵心怡，喻 平

“做数学”对初中生数学核心素养表现影响的实验研究

许天枢1，赵心怡1，喻 平2

（1．南京市金陵汇文学校，江苏 南京 210036；2．南京师范大学 数学科学学院，江苏 南京 210043）

数学课程标准将发展学生的核心素养作为课程目标，新课程实施面临的一个重要问题就是要研究如何通过知识的教学来促进学生数学核心素养的发展．以江苏省南京市某重点中学初中一、二年级学生作为被试，以教学方法为自变量，数学抽象、直观想象、逻辑推理、数学建模4种数学核心素养以及学生品格、价值观测试成绩为因变量进行教学实验研究．结果表明，实验组与对照组的后测成绩存在显著性差异，“做数学”的教学方式能够提升学生的核心素养水平，同时促进学生品格与价值观的发展．

“做数学”；核心素养；品格；价值观

1 问题提出

核心素养是学生应具备的、适应终身发展和社会发展需要的必备品格和关键能力．《普通高中数学课程标准（2017年版）》提出数学学科核心素养包括：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析[1]．《义务教育数学课程标准（2022年版）》提出，在初中阶段数学核心素养的表现为：抽象能力、运算能力、几何直观、空间观念、推理能力、数据观念、模型观念、应用意识、创新意识[2]．与高中课程标准的说法内涵基本一致，只是要求和程度上有所差异．在新课程的实施中，如何通过知识的教学来发展学生的核心素养成为数学教育理论和实践关注的问题．

自数学课程标准颁布以来，关于数学核心素养的研究主要表现在几个方面．（1）数学核心素养的评价框架建构．课程标准有对学习质量标准的具体阐述，但如何在教学实践中具体落实，需要对评价质量标准进行可操作化的体系建构．有学者研究整体评价框架[3]，也有学者对核心素养一些要素的评价作研究，例如，郑雪静等人基于范希尔理论建构了直观想象素养的评价框架[4]，陈建明等建构了包括4个维度15个二级指标的数据分析素养评价框架[5]，张和平等完成了小学生几何直观能力测评模型的构建[6]．祖丹等基于数学建模的过程性特征，从纵横两个角度，构建了双维多水平的数学建模能力测评框架[7]．（2）对学生数学核心素养的调查研究．张淑梅等对学生6个核心素养的基本情况作了调查，并讨论了6个数学核心素养之间的关系，发现6个数学核心素养之间均具有显著的相关性，其中逻辑推理和数学运算的相关性最大，并且数学运算对逻辑推理的影响比逻辑推理对数学运算的影响更大．数学建模与数据分析的素养对其它4种数学素养的依赖程度明显大于其它4种素养对它们的依赖程度[8]．严卿等对初中生的逻辑推理能力展开调查，得到一些有意义的结果[9]．类似的研究还有：数学演绎推理能力测评[10]，基于学业水平质量监测的初中生数学核心素养发展状况调查[11]，高中生数学抽象能力发展的调查[12]，高中生数学学科核心素养水平调查[13]等．（3）对中高考中各核心素养考察效果的分析．这类研究主要是针对近几年各地中考或高考题目中，对涉及数学核心素养要素的测查作分析，以评价考题的合理性[14–16]．（4）数学核心素养的内涵．易亚利等认为，小学生数学逻辑推理素养的内涵为：将现实情境转化并表述为数学问题，以小学数学概念、命题、运算法则或假设为前提，按照逻辑规则及运算规律，得出正确结论的综合能力[17]．（5）培养学生数学核心素养的教学研究．这方面的研究有理论层面的探讨，如黄秦安等认为，数学课堂文化应该贯穿数学文化的精髓，融科学精神与人文素养于一体并充分体现师生主体间性，在丰富多样的数学课堂文化模式建构及其实践中，可以通达实现数学核心素养教育的目标[18]．有学者构建了一个数学素养结构模型．在这个结构模型的基础上，进一步讨论3种教学形式：知识教学、解题教学和问题解决教学，分别对应不同层面数学素养发展的焦点[19]．吴增生采用数系扩充这种核心思想引领下整体设计与数学学科核心素养相匹配的活动的教学策略，对有理数教学实证研究，结果发现这种教学策略对学生学业水平及数学核心素养发展有积极的推进作用[20]．

由上面的研究概况可以看到，关于核心素养培养的教学研究相对较弱，特别缺少实证研究．事实上，这又是新课程实施中迫切需要研究的问题，通过怎样的教学形式，采用怎样的教学策略来发展学生的数学核心素养，这是一个新课题，新课程实施之前没有尝试，新课程实施中必须探索．当然，这个课题的研究是一个系统工程，只能采用局部到整体的策略推进．研究以教学方法作为自变量，用“做数学”作为干预因素进行教学实验，探讨“做数学”与学生数学核心素养的关系．“做数学”要求学生利用一些工具进行具体操作，从事物的变化中抽象出数学概念或模型，或者验证一个数学事实，设想这个过程与数学抽象、直观想象、逻辑推理、数学建模等4种数学核心素养表现有高相关关系，因此，选取这4个因素作为因变量，即探讨“做数学”对这4个核心素养表现的影响，并探究“做数学”对学生品格和价值观发展的影响．

2 “做数学”教学模式建构

“做数学”不是一个全新的概念，杜威的“做中学”就是“做数学”的一个原型．为改变传统的以传授为主的教学方式，20世纪中后叶美国科学学科开始实施“Hand-on”（动手做）学习计划，后逐步在美国、法国科学教育界得到推广，辐射到数学学科就是“做数学”的发端．广义地理解，做数学研究、做数学练习、解答数学问题、动手操作去发现规律或验证规律等过程，均可谓“做数学”．对“做数学”赋予新的涵义：“做数学”是学生运用材料和工具，在动手动脑相协同的过程中，通过操作体验、数学实验、综合实践等活动，理解数学知识、探究数学规律、解决问题的一种数学学习方式[21]．从外延看，“做数学”包括：（1）数学体验，即通过操作、观察、感悟、理解来学习数学．就是让学生动手操作，在操作中体验数学．由此，学生可以获得大量的感性知识．（2）数学实验，即通过操作、观察、探究、发现及论证来学习数学．就是引导学生利用一定的工具（实物或软件），通过操作感受、观察思考、归纳抽象等过程建构数学概念、验证数学结论、探索数学规律、解决数学问题．（3）综合实践，即通过思考、实践、运用、解决问题来学习数学．它以经验与生活为核心，强调学生通过实践，增强问题和创新意识，学习科学研究的方法，发展综合运用知识的能力[21]．

基于上述认识，建构如下“做数学”的教学模式．

理论基础：（1）知行结合——“做数学”的认识论基础．做的过程兼有动作与思维双重性特征，一方面，身体的结构和性质决定了认知的种类和特性，认知并非可以脱离身体的抽象符号运算；另一方面，身体和环境又是认知系统的构成成分，为思维发展奠定了基础．（2）建构知识——“做数学”的学习论基础．“做数学”是学生的个体行为，形式上表现为独立思考与合作学习相结合，知识不是通过教师的传递而获得，而是通过学生的自我建构与合作建构而获得．（3）情境认知——“做数学”的教学论基础．“做数学”体现了在情境脉络中学习，践行了在实践共同体中教学，实现了在行动中学习知识，这与情境认知理论高度吻合[22]．

教学目标：指向数学学科核心素养，包括必备品格、正确价值观和关键能力．关键能力为《义务教育数学课程标准（2022年版）》中核心素养的表现．

教学程序：3种教学样态的流程如图1所示．研究主要采用“数学实验”教学样态．

学习评价：采用测量的方法评价关键能力的发展水平，采用过程性评价方式评价学生品格与价值观的发展．

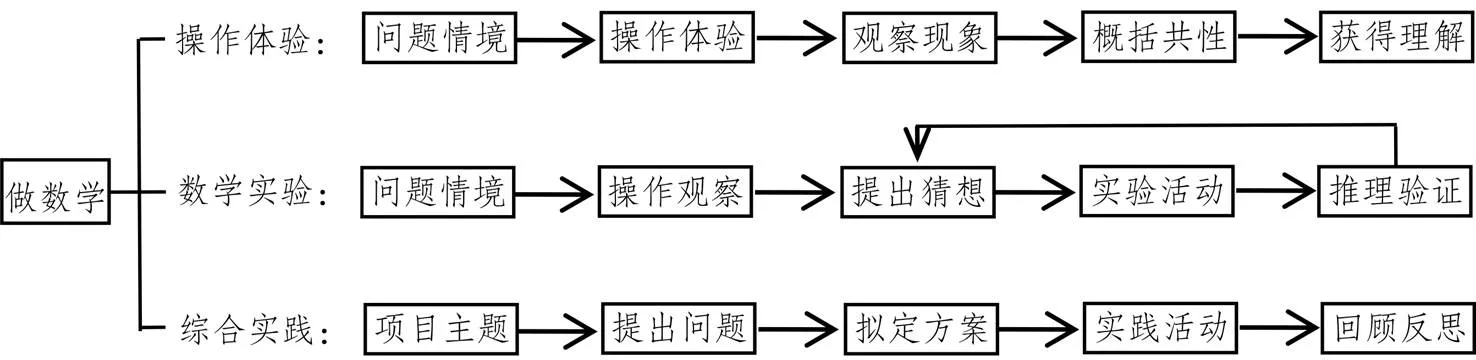
图1 “做数学”3种教学样态流程

3 研究设计

3.1 实验设计

自变量：教学方法．分为两种水平，水平1：数学实验教学方式．数学实验教学的过程见图1，具体的教学操作见后文的教学案例．水平2：常规教学方式．教学过程中不介入数学实验要素，采用教师讲授、学生接受的教学方式．

因变量：（1）数学关键能力．对初一、初二年级被试的数学关键能力作后测，考查实验组与对照组的成绩是否存在差异．（2）品格与价值观．对初二年级被试进行品格与价值观的前测和后测，考查前测与后测问卷成绩是否存在差异．

无关变量的控制：其一，实验期间，实验组与对照组被试均没有参加校外补习班的学习．其二，每组实验班和对照班都是由同一位数学教师任教，以此消除不同教师的教学水平可能造成的无关变量因素．

实验模式流程图如图2所示．图2中有“关键能力测验1”的环节，由于教学阶段1时间较短，效果不显著，因此下面的数据处理中没有介绍关键能力测验1的数据．后测成绩指关键能力测验2的成绩．由于初一年级没有进行品格与价值观的前测，因此品格与价值观的前测和后测只在初二年级进行．

图2 实验模式

3.2 被试选择

以南京市某重点初中学生作为实验对象．初一年级选取16班、18班、19班、22班；初二年级选取14班、15班、23班、24班．初一年级以入学考试的数学成绩作为参照，初二年级以初一下学期期末数学考试成绩、品格价值观问卷的成绩一同作为前测成绩，分别比较各年级4个班的成绩，作检验，确定实验班和对照班．需要说明的是，由于实验前没有单独编制关键能力的测试卷，因此以学生的学业成绩作为参考．为了弥补这个缺陷，对初一入学数学测试卷和初一下学期期末数学考试卷两套题目中，涉及数学抽象、直观想象、逻辑推理、数学建模的题目提取出来，分别对各年级4个班的学生在这4类题目得分作检验，均无显著性差异．

根据前测结果，初一年级选择18班、19班为实验组，16班、22班作为对照组，共计183人，其中女生88人，男生95人．实验组与对照组的前测成绩、4类题目成绩均不存在显著性差异．初二年级选择14班、23班为实验组，15班、24班为对照组．共计180人，其中女生84人，男生96人．实验组与对照组的前测成绩、4类题目成绩均不存在显著性差异．

3.3 研究工具

工具1：初一年级关键能力后测题目（此工具用于图2中的关键能力测试2）．关键能力测试围绕所学的知识设计，共7道题目，满分100分．因为6个核心素养不是相互独立的，它们相互交织，因此一道题考查的可能是多种关键能力．研究只考虑数学抽象、逻辑推理、数学建模和直观想象，不考虑数学运算和数据分析要素．

把关键能力分为三级水平：知识理解（水平1）、知识迁移（水平2）、知识创新（水平3）[3]；第二，把每道题目涉及的关键能力提取出来，分析其达到的水平数；第三，将题目中每道题预定的分数分解到各关键能力上去；第四，列一张表，将各关键能力的水平数及分数表示出来．计分方法：一级水平分，二级水平+1分，三级水平+2分．其中依据具体情况赋值．

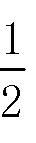
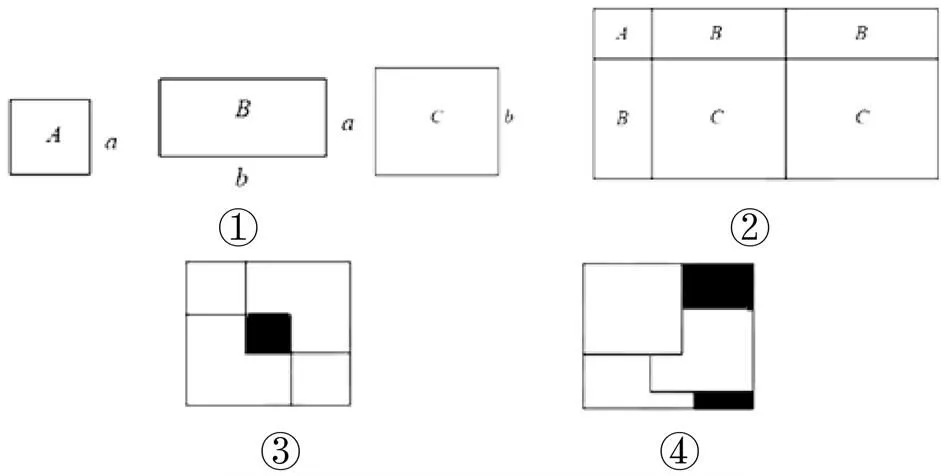
（1）用1张A型卡片，3张B型卡片，2张C型卡片拼成②形状，根据②，多项式2+3+2因式分解的结果为_____．

（2）现用A、B、C3种不同型号的卡片拼成一个边长为2+的正方形（所拼图形既无缝隙，又不重叠），则需要A型卡片______张，B型卡片______张，C型卡片_____张．

（3）现有取出3张A型卡片和1张C型卡片，将其中2张A型卡片放入1张C型卡内拼成②形状，再重新用3张A型卡片放入1张C型卡片内拼成④形状．已知④中的阴影部分的面积比③中的阴影部分的面积大2-6，则小正方形卡片的面积2=________．

第（1）题是知识在数学学科内部的迁移，需要学生借助于直观想象利用图形探索数学问题．数学抽象二级水平，直观想象二级水平．第（2）题是在第一题的基础上提出问题，从数到形的过程，数学抽象二级水平，直观想象三级水平．第（3）题是数形结合，对因式分解的应用，数学抽象三级水平，直观想象三级水平．按上述计分方法，一级水平分，二级水平+1分，三级水平+2分．此题=1分，数学抽象为4+3=7分，直观想象2+6=8分，共15分（表1）．

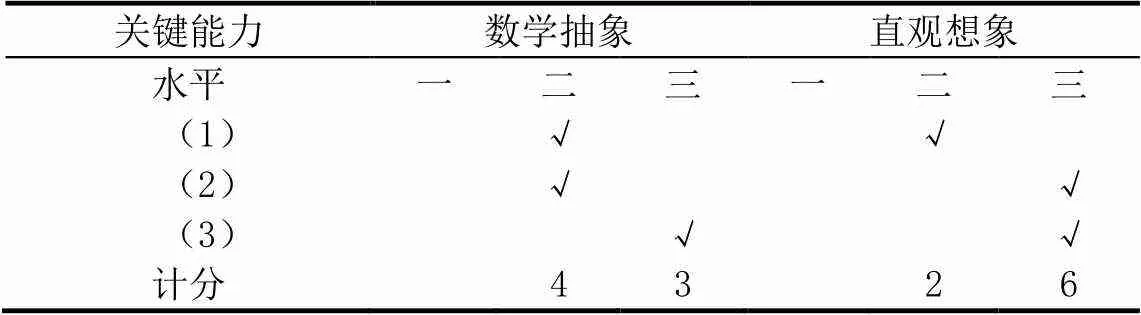
表1 初中试题样例数学关键能力水平分布情况

将关键能力测试卷分为数学抽象、逻辑推理、数学建模、直观想象分为4个维度，其克隆巴赫Alpha系数分别为0.898、0.826、0.810、0.758，总测题信度为0.965．表2显示，各维度之间的相关均小于各维度与关键能力测试卷之间的相关，因而关键能力测试卷有很好的结构效度．

表2 初一年级后测题目各维度与总分的相关系数

注:**表示<0.01，以下同．

工具2：初二年级关键能力后测题目（此工具用于图2中的关键能力测试2）．共9道题目，满分100分．与工具1的处理方式相同．

题目举例：大家都知道菱形、矩形与正方形的形状有差异，我们将菱形、矩形与正方形的接近程度称为“接近度”．在研究“接近度”时，应保证相似图形的“接近度”相等．

（1）已知菱形相邻两个内角的度数，定义菱形的“接近度”为这两个内角度数差的绝对值，于是，这个绝对值越小，菱形越接近正方形．请回答下面问题：

① 若菱形的一个内角为70度，则该菱形的“接近度”等于_______；

② 当菱形的“接近度”等于_____时，菱形是正方形．

（2）已知矩形相邻两条边长，我们将矩形的“接近度”定义为相邻两条边长差的绝对值，于是，这个绝对值越小，矩形越接近于正方形．请回答下列问题：

① 你认为这种说法是否合理？为什么？

② 如果你认为不合理，请你给出矩形的“接近度”一个合理定义．

第（1）题是知识在数学学科内部的迁移，需要学生借助于直观想象进行推理并作简单计算．更主要的是，这是一个抽象新概念的过程，没有一定的抽象能力是难以理解概念的．数学抽象二级水平，直观想象二级水平，逻辑推理一级水平．第（2）题是在证伪的基础上提出问题，抽象出一个新的概念，同时要论证这个概念的合理性，数学抽象三级水平，逻辑推理三级水平，直观想象二级水平．

将关键能力测试题分为数学抽象、逻辑推理、数学建模、直观想象分为4个维度，其克隆巴赫Alpha系数分别为0.872、0.800、0.890、0.808，总测题信度为0.982．表3显示，各维度之间的相关均小于各维度与关键能力测试卷之间的相关，表明关键能力测试卷有很好的结构效度．

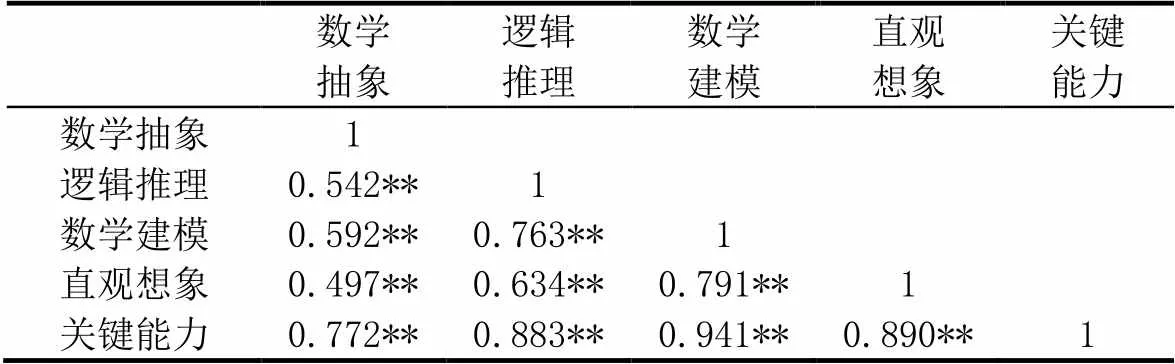
表3 初二年级后测题目各维度与总分的相关系数

工具3：品格与价值观问卷（此工具用于初二年级实验组与对照组的前测与后测）．使用喻平等编制的“中学生数学品格与价值观的问卷”[23]．该量表具有良好的结构效度．4个子量表及总量表的克隆巴赫Alpha系数分别为0.707、0.783、0.837、0.840、0.930．

4 实验过程

4.1 实验操作

整个实验持续一学期（下学期），共分为两个阶段，具体实验内容见表4、表5．

表4 初一年级“做数学”教学内容

表5 初二年级“做数学”教学内容

注：表4～5中的“手册”指2015年由江苏凤凰科学技术出版社出版的董林伟主编的《数学实验手册》．

4.2 数学实验教学案例

【初一】

在“整式乘法与因式分解”的学习中，结合数学实验手册，选择“拼图——探索一类多项式的因式分解”这一课时作为实验教学，让学生通过动手、动眼、动脑、动嘴的拼图过程，探索拼图与整式因式分解之间的内在关系．

实验工具：A型纸片（边长为的正方形）、B型纸片（边长为的正方形）、C型纸片（长为、宽为的长方形）各若干张．

（1）操作与思考．

用A型纸片1张、B型纸片2张，拼成边长为+的正方形，用不同的方法表示正方形的面积．

（2）思考与认知．

① 分别取适当数量的A型、B型、C型3种纸片，使其拼成一个长、宽分别为+3，+的长方形，并将多项式2+4+32分解因式．

② 你能否取适当数量的A型、B型、C型3种纸片，使其拼成一个长方形，并将多项式2+10+92分解因式？

问题一：你能发现图中隐含的等式吗？请将它写下来．

问题二：你能得出一般拼图的方法吗？请结合图形解释你得到的等式．

问题三：分别取适当数量的A型、B型、C型3种纸片，能拼成面积为2+5+32的长方形吗？若能，请拼出图形；若不能，请改变其中一项的系数，并拼出图形．

（3）练习．

分别取适当数量的A型、B型、C型3种纸片，请根据条件设计一个体验活动课题，尝试写出一个多项式的因式分解，撰写体验报告．

【初二】

综合实践活动课中，学生应当占据主导，通过独立思考、小组合作，推动活动的进行．教师在活动中应该扮演一个引导者和旁观者的角色．本节课让学生经历中点四边形的形成过程，知道中点四边形的形状和原四边形形状的关系，理解中点四边形形状的判断及证明方法，并能够逆向思考对逆命题做出判断举出反例，感受合作探究的过程，学会分析问题的一般方法．

（1）复习旧知．

如图，在△中，、、分别是、、的中点，则△的形状、周长、面积与原三角形△是什么关系？能简单说明理由吗？

（2）构建新知．

如图，、、、分别是四边形的边、、、的中点，试判断四边形的形状，并说明理由．

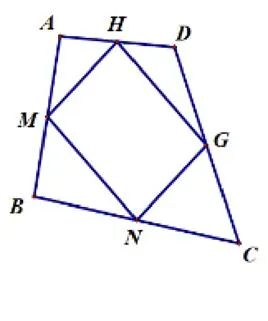
四边形是平行四边形，连接、（如图），

∵、分别是、的中点，

∴是△的中位线，

∴∥且=．

∴四边形是平行四边形．

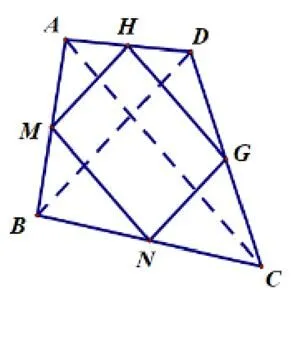
对一般四边形的中点四边形进行了讨论，一般四边形具备某方面的特殊性时，就成了平行四边形、矩形、菱形和正方形．那么这些特殊四边形的中点四边形是什么样的呢？请你做出判断并给出证明（以小组为单位探究平行四边形、矩形、菱形和正方形的中点四边形形状，并给出证明，多媒体展示）．师生合作共同完成．

（3）学以致用．

如果一个四边形的中点四边形是菱形，那么原四边形一定是矩形吗？如果不一定，请你画出其他满足条件的原四边形，并指明如果一个四边形的中点四边形是菱形，那么原四边形应当满足什么条件？（小组讨论，全班交流）你还能提出类似的问题吗？师生合作共同完成．

5 研究结果

5.1 初一年级前测和后测数据检验结果

对初一年级学生的前测没有设计专门的工具，初一年级入学时学校组织了一次入学考试，考试内容是小学所学的内容，然后将这次考试作为实验研究的前测，从学业成绩和涉及数学抽象、直观想象、逻辑推理、数学建模4个数学核心素养表现的测试成绩作分析．测试结果见表6．

表6 初一年级前测测试成绩

由表6可见，初一16班、18班均分相近，初一19班、22班均分相近，对16班、18班的均分作统计检验，结果=0.807>0.05，对19班、22班的均分作统计检验，结果显示=0.682>0.05，因此实验组、对照组入学考试测试成绩不存在显著性差异，学生学业水平相当．将实验组和对照组在试题中涉及数学抽象、直观想象、逻辑推理、数学建模4个方面的均分作检验，结果显示=0.757、=0.714均大于0.05，因此实验组和对照组被试在4个数学核心素养表现上不存在显著性差异．实验结束后，用工具1对实验组和对照组进行后测，测试结果见表7、表8．

表7 初一年级后测测试成绩

表8 初一年级后测测试成绩独立样本检验

5.2 初二年级前测和后测数据检验结果

对于初二年级的前测，以被试在初一年级下学期的期末考试成绩为依据，同时将试题中涉及数学抽象、直观想象、逻辑推理、数学建模4个核心素养表现的题目单独计分，对实验组和对照组的分数作比较．测试结果见表9．

表9 初二年级前测测试成绩

表9显示实验组与对照组的平均成绩差异不大，经过对实验组和对照组的均分作统计检验，数据显示分别为=0.759、=0.908均大于0.05，说明实验组与对照组初一年级下学期期末数学考试成绩不存在显著性差异，学生学业水平相当．将实验组、对照组在试题中涉及数学抽象、直观想象、逻辑推理、数学建模的题目的均分作检验，结果显示=0.805、=0.798均大于0.05，实验组和对照组被试在4个数学核心素养表现上不存在显著性差异．

同时，实验之前用工具3对初二年级实验组和对照组进行测试，测试结果见表10．

表10 初二年级品格价值观问卷前测成绩

表10显示对应的实验组和对照组品格与价值观的成绩差异不大．再对实验组和对照组的成绩作统计检验，结果显示，14班与15班的均分比较=0.978>0.05；23班与24班的均分比较=0.645>0.05，实验组、对照组品格价值观问卷成绩不存在显著差异．

实验结束后，用工具2对初二年级被试进行后测，测试结果见表11和表12．

表11 初二年级关键能力问卷后测成绩

表11显示，以被试进行关键能力的测试成绩对应的实验组和对照组之间的均分差异不大，进一步作检验，结果见表12．数据显示14班与15班的均分比较=0.004<0.01；23班与24班的均分比较=0.001<0.01，经过效应量计算，Cohen’s分别为0.613、0.733，属于中等效应．表明实验组与对照组的在4个核心素养的表现方面存在非常显著的差异．因此，进一步证实经过“做数学”的教学干预后，实验组和对照组在4个核心素养的表现方面上产生了显著差异，实验组的成绩显著高于对照组，即“做数学”可以促进学生数学核心素养的发展．

同时，用工具3对初二年级实验组和对照组进行后测，统计数据见表13和表14．

表12 初二年级关键能力后测测试成绩独立样本检验

表13 初二年级品格价值观后测测试成绩

表14 初二年级关键能力后测测试成绩独立样本检验

从表13的数据可以看到，实验组的均分高于对照组的均分，经过统计检验，表14显示14班与15班的均分比较=0.000<0.01；23班与24班的均分比较=0.000<0.01，经过效应量计算，Cohen’s分别为0.804和0.865，属于大效应．因此，实验组与对照组的品格与价值观后测成绩存在非常显著的差异．

分别在初一年级和初二年级分别开展实验，在实验组和对照组学业水平相当，数学抽象、直观想象、逻辑推理、数学建模4个数学核心素养表现水平不存在显著性差异的前提下，进行“做数学”的实验干预，后测结果显示实验组与对应的对照组在4个核心素养表现方面均存在显著性差异，表明“做数学”的教学方式对于提升学生的数学核心素养有积极的推进作用，进而验证了研究假设：“做数学”的教学形式能够促进学生数学抽象、直观想象、逻辑推理、数学建模的发展，促进学生品格与价值观的发展．

6 研究讨论

实验表明，通过“做数学”教学方式，可以提高学生数学抽象、逻辑推理、数学建模和直观想象等关键能力，同时，这种教学方式还能够促进学生品格与价值观的发展．因为没有找到类似的研究，不好作比较，只能从“做数学”本身来分析产生这些效果的原因．

杜威认为，在理想的教学过程中，教师应当鼓励儿童在活动时开动大脑，运用观察和推测、实验和分析、比较和判断，使他们的手、足、耳、目和头脑等身体器官成为智慧的源泉[24]．事实上，杜威的“做中学”得到了具身认知理论的支持，其基本要点是知与行的结合，能够促进学生智慧的增长．从“做数学”的基本要素看，首先，数学实验是知与行完美结合的体现．对于小学生和初中生来说，他们具备的知识量有限，思维也没有上升到能够完全依托符号表征来完成思维的水平，因而在发现知识、理解知识方面仍需要动作表征或表象表征的支持．因此，学生思维的发展离不开知行的结合．其次，综合实践也是融认知与行为为一体的活动，将数学知识用于实践，解决与现实生活或其它学科相关的问题，这不仅发展了学生自身的认知能力，也增强了他们的实践能力．也就是说知行结合，是发展学生数学抽象、逻辑推理、数学建模和直观想象等关键能力的必要条件．

“做数学”的特征表现为：（1）主体性与交互性．“做数学”的主体是学生，学生通过认知与情感的参与使思维得到发展；同时，“做数学”又是学生间的交互合作与经验共享的过程．（2）情境性与实践性．情境性强调“做数学”的学习素材与现实生活的联系，强调问题探究与实践活动的开展．（3）开放性与教育性．“做数学”的形式、内容、结果等都是开放、多元的，而且活动过程中蕴含着素养、能力、情感态度和价值观培养的要素[25]．通过“做数学”的特征可以看到，学习活动注重学生的体验和实践，所以做的形式是多样的，做的内容是开放的，做的结果又是动态、可误的数学知识．无论哪种形式的“做数学”都要容许学生“犯错”，允许不同的想法出现，引发大家的思考，发展学生的创新思维和学习能力，在学生的交流合作中发现数学本质，建构新知．“做数学”的过程仅是载体，学生操作与实践活动等行为的最终目的不只是满足于完成某一任务或获取某些数学原理与知识，而更要注重培养学生探究与应用数学的各种能力、认识现实世界的一般方法以及随之而来的对数学价值的体悟认识和积极的情感态度等，从而能够促使学生素养的全面和谐发展．

研究也存在一些问题，一是实验仅限于一所学校，样本量偏小，特别是对品格与价值问卷的测试，样本量更小；二是实验时间不长，可能会影响结果的外在效度；三是前测缺少对数学核心的检测，可能没有做到完全意义上的随机化分组．因此，后面的工作是扩大实验样本，设计更加精准的实验模式开展研究．

7 研究结论

（1）采用“做数学”的教学方式，可以使学生的数学抽象、直观想象、逻辑推理、数学建模等关键能力得到提升．

（2）采用“做数学”的教学方式，可以促进学生数学品格与价值观的发展．

[1] 中华人民共和国教育部．普通高中数学课程标准（2017年版）[M]．北京：人民教育出版社，2018：6．

[2] 中华人民共和国教育部．义务教育数学课程标准（2011年版）[M]．北京：北京师范大学出版社，2012：5-6．

[3] 喻平．数学核心素养评价的一个框架[J]．数学教育学报，2017，26（2）：19-23，57．

[4] 郑雪静，陈清华，王长平，等．高中生直观想象素养的测量与评价研究[J]．数学教育学报，2020，29（4）：7-12．

[5] 陈建明，孙小军，杨博谛．数据分析素养的评价框架与实施路径研究[J]．数学教育学报，2022，31（4）：8-12．

[6] 张和平，裴昌根，宋乃庆．小学生几何直观能力测评模型的构建探究[J]．数学教育学报，2017，26（5）： 49-53．

[7] 祖丹，丁锐，孔凡哲．双维多水平数学建模能力测评框架的构建[J]．数学教育学报，2022，31（4）：56-61．

[8] 张淑梅，何雅涵，保继光．高中数学核心素养的统计分析[J]．课程·教材·教法，2017，37（10）：50-55．

[9] 严卿，喻平．初中生逻辑推理能力的现状调查[J]．数学教育学报，2021，30（1）：49-53，78．

[10] 郝连明．数学演绎推理能力测评研究——以八年级学生为例[J]．数学教育学报，2022，31（4）： 14-20．

[11] 董林伟，喻平．基于学业水平质量监测的初中生数学核心素养发展状况调查[J]．数学教育学报，2017，26（1）：7-13．

[12] 郭民，史宁中，朱立明，等．高中生数学抽象能力发展水平划分与基于水平划分的调查研究[J]．课程·教材·教法，2017，37（6）：124-131．

[13] 于川，朱小岩，邬楠，等．高中生数学学科核心素养水平调查及分析[J]．数学教育学报，2018，27（2）：59-64．

[14] 倪黎，茹凯，颜宝平．“数学建模”核心素养试题分析与命题探索[J]．数学教育学报，2022，31（2）：69-76．

[15] 朱先东，吴增生．核心素养视角下对数学测评的研究——以2017年浙江省中考试题为例[J]．数学教育学报，2017，26（5）：36-43．

[16] 俞梦飞，章飞．核心素养视角下数学高考试卷评价研究——以2018和2019年江苏高考卷为例[J]．数学教育学报，2020，29（2）：35-40．

[17] 易亚利，宋乃庆，胡源艳．小学生数学逻辑推理素养：内涵价值表现形式[J]．数学教育学报，2022，31（4）：28-31．

[18] 聂晓颖，黄秦安．论数学课堂文化的内涵与模式及对培养数学核心素养的价值[J]．数学教育学报，2017，26（2）：71-74．

[19] 宁锐，李昌勇，罗宗绪．数学学科核心素养的结构及其教学意义[J]．数学教育学报，2019，28（2）：24-29．

[20] 吴增生．数学学科核心素养导向下的有理数教学实证研究[J]．数学教育学报，2020，29（2）：53-57．

[21] 董林伟．走向学科育人：“做数学”的时代建构与实践创新[J]．教育发展研究，2021（8）：1-17．

[22] 喻平．“做数学”的理论基础分析[J]．教育研究与评论，2021（6）：22-26．

[23] 喻平，董林伟，郭庆松．中学生数学品格与价值观的问卷设计[J]．数学教育学报，2021，30（4）：12-18．

[24] 约翰·杜威．民主主义与教育[M]．王承绪，译．北京：人民教育出版社，2001：25．

[25] 董林伟，石树伟．做数学：学科育人方式的实践创新[J]．数学通报，2021，60（4）：22-24，62．

An Experimental Study on the Influence of “Doing Math” on the Performance of Mathematics Key Competencies of Junior Middle School Students

XU Tian-shu1, ZHAO Xin-yi1, YU Ping2

(1. Nanjing Jinling Huiwen School, Jiangsu Nanjing 210097, China;2. Institute of Curriculum and Teaching, Nanjing Normal University, Jiangsu Nanjing 210097, China)

Mathematics curriculum standards take the development of students’ key competencies as the curriculum objective. An important problem faced by the implementation of the new curriculum is to study how to promote the development of students’ key competencies through knowledge teaching. Taking the first and second grade students of a key middle school in Nanjing, Jiangsu Province as the participants, the teaching methods were taken as the independent variables, the four mathematical core qualities of mathematical abstraction, visual imagination, logical reasoning and mathematical modeling, as well as the students’ character and values test scores were taken as the dependent variables. The results show that there is a significant difference in the post-test scores between the experimental group and the control group. The teaching method of “doing math” can improve students’ key competencies levels and promote the development of students’ character and values.

“do math”; key competencies; character; values

G632

A

1004–9894（2023）05–0055–07

许天枢，赵心怡，喻平．“做数学”对初中生数学核心素养表现影响的实验研究[J]．数学教育学报，2023，32（5）：55-61．

2023–08–08

江苏省教育科学“十四五”规划2021年度重大课题——学科育人视角下“新教学”体系构建研究（A/2021/07）；江苏省教育科学“十四五”规划2021年度重点课题——指向育人方式变革的初中数学体验教学模式建构研究（B/2021/02/02）

许天枢（1977—），男，江苏南京人，中学高级教师，江苏省特级教师，主要从事数学课堂和数学教育研究．

[责任编校：陈隽、张楠]