引导语对小学生数学问题提出表现的影响——以平均数为例

陈 婷，孙琪琪，蔡金法

引导语对小学生数学问题提出表现的影响——以平均数为例

陈 婷1，2，孙琪琪2，蔡金法3

（1．西南大学 基础教育研究中心，重庆 400715；2．西南大学 教育学部，重庆 400715；3．特拉华大学 数学系，特拉华 纽瓦克 19716）

问题提出可以作为一种诊断学生数学概念理解的评估工具，问题提出引导语又关乎问题提出的诊断结果．为考察引导语对小学生问题提出表现的影响，以平均数为例，设计3套不同引导语的平均数问题提出测试卷，随机选取某公立小学262名六年级学生为测试对象，从问题得分、类型、难度和概念理解程度4方面分析引导语对学生问题提出表现的影响．研究发现：小学生在平均数上具有较好的问题提出表现；不同问题提出引导语显著影响学生问题提出的类型和难度；在较复杂的问题情境中，问题提出引导语显著影响学生的平均数理解程度．

问题提出；问题提出引导语；平均数

1 问题提出

近年来，问题提出在改善教学、促进学生概念理解等方面的作用日益受到关注．对学生而言，数学问题提出指：

（1）学生能够根据已有情境提出包括数学表达式和数学图表的数学问题；（2）学生能添加合理信息重构原有问题[1]．对教师而言，问题提出是一种教学手段，也是一种教学目标[2]．目前关于问题提出的研究主要是将问题提出作为一种教学手段[3]，考察其在课堂教学中对学生的概念理解以及数学学习的促进作用[4]，许多研究将问题提出作为一种评估手段[5]，通过学生提出问题的类型有效评估其概念理解情况[6]．他们认为学生提出问题必须基于对情境中信息的分析与提取和对相关概念和知识的理解，因此，教师能够通过学生提出的问题更加全面地观察学生的学习过程，从而有效评估学生的数学理解．已有数学问题提出的研究主要围绕师生所经历的问题提出过程展开[7]，也有学者探究了影响学生问题提出的变量，发现问题提出与数学情境、引导语密切相关[8]．问题提出引导语即教师在进行问题提出教学时采用的提示性话语，能引导学生提出数学问题，进而有效落实数学课程标准对学生提出问题能力的目标要求．引导语主要分为两大类：一类是基本信息引导语，包含情境引导、数目引导、交流引导、知识或策略引导、学科引导、解答引导6种，另一类是疑问式引导语，引导学生提出疑惑式数学问题[9]．面对不同类型的问题提出引导语，学生有不同的思维过程，他们问题提出表现也不尽相同．关注学生的问题提出表现，从认知层面分析学生对数学概念的理解程度，从而培养学生的问题意识和思维能力[10]．为了帮助教师深入了解学生对数学概念的认知过程，研究选择“平均数”概念进行分析，为提升数学教师的问题提出教学提供参考．

平均数是小学数学知识中的一个基本统计概念，也是日常生活和统计分析中不可或缺的存在．《义务教育数学课程标准（2022年版）》明确指出要“重视平均数统计意义的理解”[11]，平均数的教学要从“算法理解、概念理解、统计理解”3个方面引导学生理解平均数．也就是说，在小学阶段，平均数涉及算术程序性理解、算术概念性理解以及统计概念性理解3种类型[12]，包括“平均分配”的计算过程、灵活使用算法解决复杂的平均数任务情境以及作为统计量刻画数据的集中趋势，并利用平均数进行不同组别数据的比较等方面．关于平均数概念的理解及其发展过程，部分研究多以国外学生作为研究对象，涉及内容包括其对于平均数各种概念类型的探究[13-15]．如Strauss和Bichler的一项研究表明，不同年龄阶段的学生学习平均数的难易程度不同，在理解平均数性质方面也存在显著差异[16]．关于学生对平均数的算术概念理解情况，蔡金法等人的研究结果表明，中美两国六年级学生都能正确计算简单的平均数问题，且中国学生的总体表现好于美国学生，但对于某些复杂问题，两国学生均缺乏对平均数算法的概念性理解[17]．而对于平均数的统计理解，Watson等通过访谈分析将“学生能够运用平均数比较图表中的数据集”视作平均数概念理解的较高水平[18]．由于平均数概念的复杂性，学生并不能对其进行完全的理解．特别是在统计理解方面，不少学生常常把所给数据作为一些离散的点，而不是作为一个整体看待，导致混淆了平均数、中位数和众数这些统计概念[19]．然而，目前国内关于学生平均数概念理解情况的研究较少，结合问题提出手段考察学生平均数概念理解的研究较为欠缺，对于问题提出引导语与学生问题提出表现的关系也缺乏在相同情境下的探讨．因此，研究将采用平均数问题提出测试卷，探究不同问题提出引导语下学生的问题提出表现．具体的研究问题为：不同问题提出引导语下学生提出问题的得分有何差异？学生提出问题的类型是否存在差异？问题提出引导语对学生提出问题的难度有无影响？不同问题提出引导语下学生对平均数概念的理解程度是否存在差异？

2 研究方法

2.1 研究对象

通过方便取样的办法随机选取某市一所普通公立小学六年级的6个班共计262名学生，其中男生137名，女生125名．根据问题提出引导语的不同，将其按学号随机分为3组，第一类引导语对应的学生作为第一组，第二类引导语对应的学生作为第二组；第三类引导语对应的学生作为第三组．3类引导语下文详细陈述．调查时间安排在六年级的第一学期．

2.2 研究工具

研究采用测试的方法，测试时长为40分钟．平均数问题提出测试卷包括4个问题情境任务，分别简称为“帽子问题”“成绩问题”“书籍问题”“幼崽问题”，要求学生根据每个情境提出3个数学问题．该测试卷来自于已有研究成果，信效度已经过验证[20]．问题提出引导语分为3类：第一类引导语要求学生“提出3个不同的数学问题，挑战数学老师来解答”；第二类引导语要求学生“提出3个难度不同（简单、中等、较难）的数学问题”；第三类引导语要求学生“提出3个不同的数学问题，挑战同班同学来解答”．3类问题提出引导语皆限定了提出问题的数量，只在问题的具体要求上存在差异．测试卷内容与引导语见表1．

表1 平均数问题提出测试题与3种类型问题提出引导语

2.3 数据回收及处理

研究共发放测试卷262份，回收测试卷262份，问卷回收率和有效率均为100%．对于学生问题提出的表现，参考胡睿[20]和蔡金法[21]等人的编码框架，被试所提出的每一个问题都包含4个方面的编码：问题得分、类型、难度和概念理解程度（见表2）．“问题得分”部分，从合理性、拓展性和创新性3方面对平均数问题提出测试卷中学生所提问题进行评价，当学生3个问题均为错误问题时，只记最高得分，当学生3个问题中包含至少一个可解的数学问题时，只累加正确问题的得分．“类型”部分，将问题划分为7种类型．前3个类型“求和”“比较”“分配”不属于平均数范畴；“平均”“表征”“最值”“判断”这4个类型属于平均数范畴，其中“平均”类型问题涉及平均数的简单计算，“表征”“最值”“判断”3类问题涉及平均数的统计性概念理解．为了与引导语2的任务要求保持一致，“难度”部分将解题步骤为1～2步的问题确定为简单难度，步骤为3步的问题为中等难度，4步及以上的问题确定为较难难度．通过这一方式对所有问题的难度进行编码，统计形成各测试题难度分布情况．“概念理解程度”主要分为：（1）“平均数的算术程序性理解”，即学生知道“平均分配”，能够求出平均数和总数；（2）“平均数的算术概念性理解”，即学生能灵活使用算法解决复杂的平均数任务情境；（3）“平均数的统计性概念理解”，具体而言就是学生知道平均数作为统计量可以刻画数据的集中趋势，还能利用平均数比较不同组别的数据．为保证研究的信度，另请一位熟悉问题提出的数学教育研究人员进行核查，在每个班级的样本中各随机抽取30%样本数据进行独立编码分析，两位研究者在“平均数问题提出测试卷”的编码一致性程度超过90%，具有良好的信度．

3 研究结果与分析

3.1 3组学生的问题得分情况

通过对3组学生4个任务情境所提问题的得分进行描述性统计分析（见表3），发现除“帽子问题”外，3组学生最低分均存在低于3分的情况，也就是学生所提的3个问题均为错误问题．通过对具体任务进行分析，在4个任务情境中，第一组学生在“帽子问题”的得分为8.7分，表现最好，在“书籍问题”和“幼崽问题”的表现最差．第三组学生在“成绩问题”和“书籍问题”的表现优于其他两组，第二组学生在“幼崽问题”的表现更好．就差异性而言，不同问题提出引导语下3组学生提出合理性问题的数量不存在显著差异．

表2 平均数数据分析框架

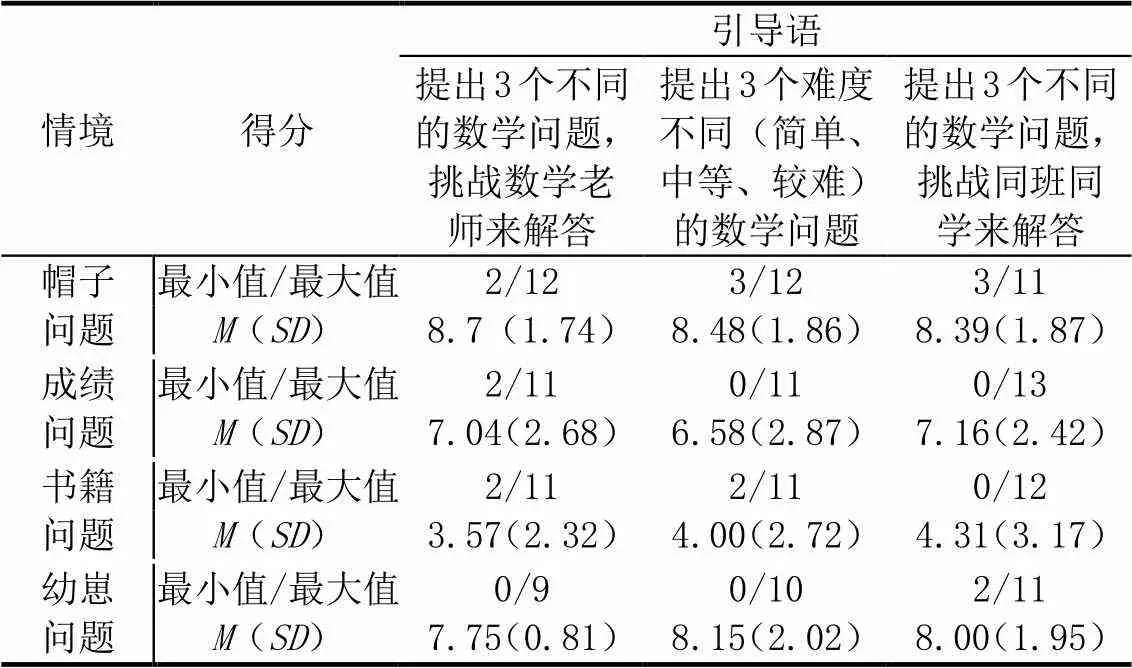
表3 3组学生在4个任务上的问题得分的描述统计

关于“帽子问题”和“幼崽问题”，3组学生的平均得分均在7.5分以上，表明越是题干信息丰富的任务情境，学生越容易提出可解的数学问题．而“成绩问题”和“书籍问题”的信息较少，特别是“书籍问题”，需要学生自己提取信息或者补充条件，对学生的挑战更大，导致“书籍问题”的得分最低，3组学生的表现最差．其原因在于“书籍问题”只有一个数学信息，需要学生自己添加合理信息提出问题，题目背景信息与给定条件的多寡对学生提出问题的准确性产生了影响．

3.2 3组学生所提问题类型的差异

根据数据分析框架对合理问题进行编码（见表4），研究发现，不同测试题学生所提问题的类型分布情况各有不同，卡方分析发现，在“成绩问题”和“书籍问题”的第一个问题中，3组学生所提问题的类型与引导语显著相关（2=19.13，=0.039<0.05；2=19.64，=0.033<0.05），且在任务情境只涉及两个数学信息情况下，不同问题提出引导语下学生提出问题的类型不同，相比于第一种和第二种引导语，第三种引导语更能引导学生提出多样的数学问题，更能激发学生的创造性．

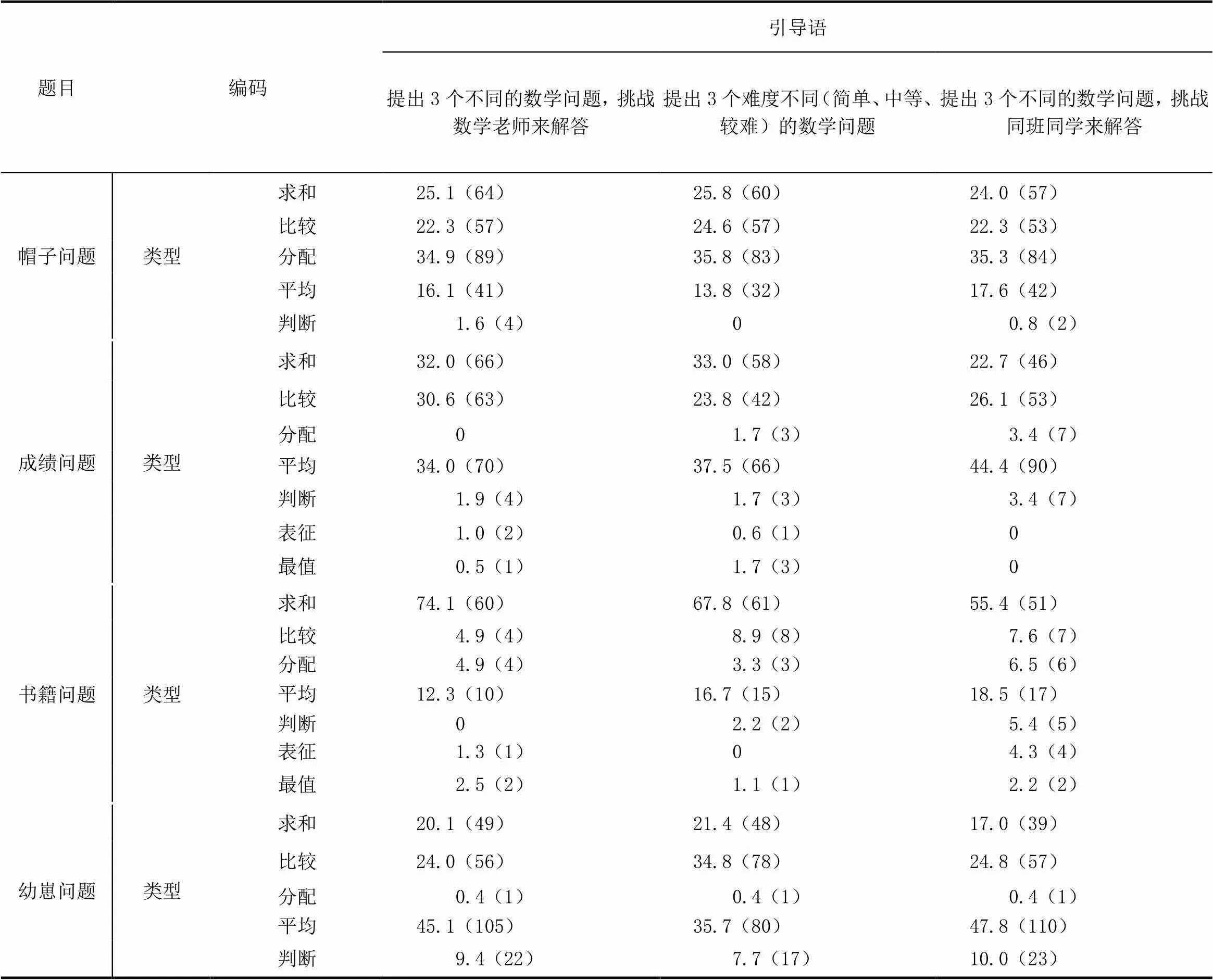
表4 3组学生问题提出类型占比

总体来看，学生更倾向于提出“求和”类型和“比较”类型的问题．除“帽子问题”外，其余3个任务情境涉及“分配”类问题占比较少，通过对分配类问题进行归类，学生提出的多为“加入新数，把平均数提升至目标数”的问题．根据分析框架，计算出4个情境中属于平均数范畴的类型占比，3组学生在“成绩问题”和“幼崽问题”提出直接涉及平均数的问题占比均高于30%，表明大多数学生能够理解平均数的实际意义．其原因在于，两个题在题干信息提示了“老师将其中的最高分和最低分去掉”“想知道猫和仓鼠哪一种一次生的幼崽更多”，学生不用补充条件也可以提出例如“去掉最高分和最低分，小明剩下8项测试的平均分为多少分”，“猫平均一次生崽多少只”这一“平均”类型问题．在“成绩问题”中，第三组的学生未能和其余两组一样提出“表征”和“最值”类问题．在“帽子问题”中，第一组和第三组的少数学生能够添加合理信息，提出蕴含统计思想的“判断”类问题．而在“书籍问题”中，第一组的学生未能和其余两组一样，提出蕴含统计思想的“判断”类问题．值得注意的是，在“书籍问题”中，学生所提问题的类型最丰富，特别是第三组的学生，在原有任务情境基础上，开辟新的视角，提出了涉及平均数概念理解和统计理解范畴的问题．如根据题目给出的信息，学生提出求书籍的最高价，最低价等可能性问题，蕴含平均数没有必要等于某个数据的“最值”类型问题．

3.3 3组学生提出问题的难度分布

研究以学生所提问题解答所需的常规步骤作为题目难度的表征，学生所提问题在各个难度值上均有不同程度的分布（见表5），简单和中等难度的问题占到总体的70%以上．由此可见，虽然大多数学生能够提出可解答的、恰当的数学问题，但是难度值较高，思维挑战度较大的问题占比较少．除“成绩问题”外，各难度的占比依次递减．这与已有研究结果一致，当学生被要求提出3个数学问题时，他们更倾向于提出相关的平行问题或链式问题．在“书籍问题”中，明确要求提出3种类型问题的第二组学生合理问题的占比最高，其所提的较难问题占比也高于其他两组，表现较好．关于“成绩问题”，3组学生较难问题的占比都超过25%，其原因可能在于“成绩问题”涉及信息的复杂性足以使学生不用补充条件就可以提出较难的问题．

在“成绩问题”的第一个和第三个问题上，3组学生所提问题的难度与其对应的引导语存在显著相关关系（2=13.47，=0.036；2=22.4，=0.001），即针对不同的问题提出引导语，学生提出问题的难度是不同的，第二种引导语的学生则问题难度呈依次递增趋势，与引导语要求一致，第一种引导语和第三种引导语的学生倾向于提出简单难度的问题，中等难度和较难难度的问题占比比较均衡，但第一组学生较难问题的占比高于第二组．在“书籍问题”的第一个问题上，第一种和第二种引导语的学生更倾向于提出简单难度的问题（2=14.82，=0.022）；在第三个问题上，第二种引导语的学生更倾向于提出简单和较难难度的问题，第三种引导语的学生更倾向于提出简单和中等难度的问题（2=13.23，=0.04）．

3.4 不同问题提出引导语下学生的平均数理解程度情况

研究对3组问题提出引导语下学生的平均数理解程度做了统计（见表6），分析不同问题提出引导语对他们概念理解程度的影响．卡方分析表明，在“成绩问题”和“书籍问题”，不同问题提出引导语下学生的平均数理解程度存在显著差异（2=13.68，=0.008；2=18.52，=0.001）．在“成绩问题”中，第三种引导语的学生处于平均数统计性概念理解阶段的人数多于前两种引导语的学生．在“书籍问题”中，第一种引导语的学生处于平均数的算术程序性和概念性理解阶段，第三种引导语的学生更注重平均数统计性概念理解．其原因可能为：在提出问题过程中，学生要涉及编辑信息—选择信息—理解信息—转换信息4个部分[22]，“成绩问题”和“书籍问题”更侧重考察学生对信息的理解与转换，对学生认知要求高，最终导致3组学生在这两个平均数任务情境中的理解程度存在显著差异．此外，第三种引导语的挑战对象是同学，学生更愿意提出多样的数学问题．

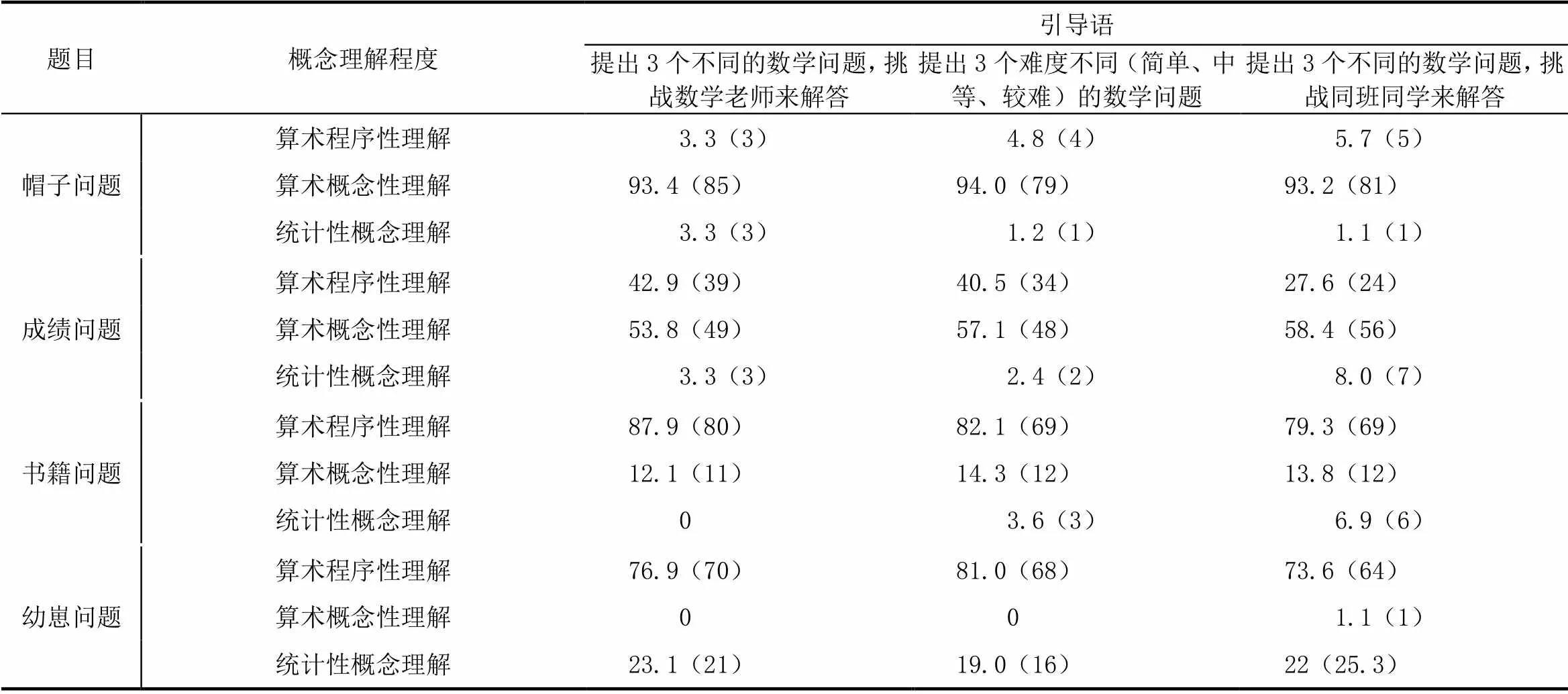
表6 学生的平均数理解程度占比情况

总体而言，3组学生在平均数算术程序性理解和算术概念性理解上的表现优于在平均数统计性概念理解上的表现．大部分学生掌握了平均数的算术程序性理解和平均数的算术概念性理解，熟悉“相加并除”这样类似平均分的算法，也可以灵活使用平均数算法解决复杂的平均数任务情境，但其发展水平并不同步[23]．如“书籍问题”着重考查学生对平均数的统计性概念理解，需要学生理解10本书的平均价格是代表这10本书的一个数据，不一定每一本书的价格都是平均价格．对于大部分学生而言，基于已有条件，仅能提出“10本书的总价是多少”这类涉及平均数的算术程序性理解的数学问题，这也说明学生对于平均数的算术概念性理解和统计性概念理解程度不深．但也有学生提出“买10册书需要多少元”这样的问题，他们用平均数代表数组（10本书），而非作为数组中的一个数（书的单价）．“幼崽问题”中，部分学生掌握了平均数的统计意义，知道平均数具有一组数据集的代表性，可以作为典型值对几组数据进行比对．

4 研究结论及讨论

4.1 小学生在平均数上具有较好的问题提出表现

以262名六年级学生作为测试对象，初步调查六年级学生在不同引导语下的问题提出现状，发现大多数学生在平均数方面的问题提出表现较好，能够提出贴合情境可解的数学问题．在问题得分维度，3组学生在图文信息不够丰富的“书籍问题”上的表现均弱于另外3道测试题．第二种和第三种问题提出引导语的学生在“帽子问题”情境至少能提出一个以上的正确的、可解答的数学问题，甚至少数学生还能进行拓展和创新．其原因可能是第二类和第三类引导语鼓励学生提出简单、合理的问题，且“帽子问题”的信息更加丰富，对于不常接触问题提出的学生也容易入手．这与已有的同类研究结果一致，大多数小学生具有较高水平的问题提出表现，说明数学问题提出在培养学生数学思维、创新能力方面的作用越发得到重视，问题提出也为学生问题提出过程中发散思维、求异思维的运用提供学习支撑[24]．

4.2 不同问题提出引导语显著影响提出问题的类型和难度

研究结果表明，问题提出引导语对学生提出问题的类型和难度都存在显著相关．根据平均数问题提出表现的测试情况，结果表明，大多数学生能够提出五花八门的问题，但其问题提出表现仍需进一步提升．从类型来看，有超过40%的学生的思维停留在简单的运算上，且他们提出的问题类型多为“求和”“比较”“分配”，而“最值”和“表征”类问题最少，说明部分学生未能完全掌握平均数的意义，不太清楚可以用平均数描述和表征一组数据．在“成绩问题”和“书籍问题”情境的第一个问题，不同组的学生提出问题的类型也不同，特别是第三组学生在“书籍问题”所提问题的类型比其他两组学生的更丰富．原因可能是第三类引导语是挑战同班同学回答，学生的积极性增强，更愿意对问题进行拓展，提出更加新颖的问题．也可能是大多数学生只是通过改变某个条件提出了不同的问题，部分同学甚至所提的问题在难度或类型上完全没有变化，导致学生所提问题的类型在第一个问题上差异明显．

从所提问题的难度来看，第一类引导语是以教师为提问对象，旨在引导学生提出更高难度的数学问题，第二类引导语直接规定问题难度，将其划分为简单、中等和较难3组难度，最后一类引导语则是以同班同学为对象，偏重引导学生提出更多合理的数学问题．3类引导语的学生提出较难问题的比例并不高，部分学生为了提问而提问，出现低水平的重复；另一方面，虽然学生都积极参与问题提出，注重问题的新颖性，但是部分问题欠缺信息，属于不可解的问题．通过3组比较，分析问题提出引导语对不同学生所提问题的影响程度．研究发现，问题提出引导语在“成绩问题”“书籍问题”的第一个和第三个问题上对学生所提问题难度的影响更为显著．可能的原因主要有两个方面：一是引导语涉及对象不同，学生预设的问题难度也不同；二是难度较大的问题需要更多的思考时间，对学生的认知要求更高，差异也就更为明显；三是问题情境本身具有一定的难度，且这些难度具有差异性和特定性．其中，“成绩问题”和“书籍问题”不仅需要学生理解信息，还需要合理编辑与选择信息，对他们来说难度较大．研究结果表明，尽管3组问题提出引导语都有利于引导学生提出数学问题，但更具体的要求可以促使学生更多地思考问题提出的情况，从而使他们进行更深入的数学思考．

4.3 较复杂问题情境中问题提出引导语显著影响学生的平均数理解程度

在4个任务情境中，部分学生提出了错误问题，但可以通过其余的数学问题评估其对于平均数的理解．卡方分析表明，在“成绩问题”和“书籍问题”，不同问题提出引导语下学生的平均数理解程度存在显著差异．第三种引导语的学生对平均数统计性概念理解程度优于其他两种引导语的学生．整体来看，3组学生所表现出的对平均数的算术程序性和概念性理解优于对平均数的统计性概念理解，但有很大比例的学生只停留在平均数的直接应用上，主要集中在计算平均数或利用平均数求和．具体而言，第一组的学生多处于平均数的算术程序性理解和统计性概念理解阶段，第二组的学生多处于平均数的算术程序性和算术概念性理解阶段，第三组的学生多处于平均数的算术概念性理解和统计性概念理解阶段．

5 结束语

问题提出能够帮助教师了解学生在平均数概念理解的思维过程，结合研究结论及已有文献[25-28]，得到以下启示．第一，教师在进行教学时，应注重设计多样的问题提出引导语，创设“真实”情境，引导学生利用已有数学信息进行提问，在课堂中培养学生的问题提出能力．第二，学生在进行数学概念的学习时，应重视对概念的意义的理解而非仅仅会计算．第三，不同问题提出引导语的作用不同，教师应根据学生具体情况选择合适的问题提出引导语，对于基础较薄弱的学生，可以侧重于引导学生发现某种数学事实或提出预答式数学问题或引导学生提出疑惑式数学问题．对于中等学生或学优生，则引导他们提出各种各样难度不同的问题，提升信息提取能力和创新能力．此外，引导学生之间互相进行问题提出，也有利于培养学生的数学思维以及提高学生的问题提出能力．

研究定量分析六年级学生在不同引导语下的平均数问题提出表现，弥补了当前问题提出实践研究的些许不足，为一线教师开展问题提出教学、评估学生概念理解提供了参考，但仍然存在一定的局限性．第一，由于研究者将测试时间限定为40分钟，出现了部分学生尚未提出问题的情况，不能完全确定学生缺乏对平均数的统计性概念理解．第二，样本选取有一定局限性，因而所得结论可能并非对所有学生都适用．第三，样本来自6个班级，其任课教师不同，可能会影响学生的问题提出表现．为弥补以上研究的不足，未来还可在原来测试卷的基础上对问题数量或者测试时间进行完善和改进．例如，当减少任务情境数量或者延长测试时间时，掌握平均数统计意义的人数是否会增加．此外，在今后的研究中，也会直接对不同地区、不同学校的教师和学生进行教学实验，以检验引导语在问题提出教学中对学生平均数理解的影响效果．

[1] CAI J, HWANG S. Learning to teach through mathematical problem posing: Theoretical considerations, methodology, and directions for future research [J]. International Journal of Educational Research, 2020 (102): 101 391.

[2] KILPATRICK J. Problem formulating: Where do good problems come from? [M] // SHOENFELD A H. Cognitive science and mathematics education. Hillsdale: Lawrence Erlbaum Associates, 1987: 123.

[3] 许天来，蔡金法．美国数学课程中的“问题提出”——期望与挑战[J]．数学教育学报，2019，28（2）：18-23．

[4] 陈婷，徐红，徐冉冉，等．数学教师学习使用“问题提出”教学法的个案研究——以“用字母表示稍复杂的数量关系”为例[J]．数学教育学报，2019，28（2）：7-12．

[5] 蔡金法，姚一玲．数学“问题提出”教学的理论基础和实践研究[J]．数学教育学报，2019，28（4）：42-47．

[6] TICHA M, HOS PESOVAA. Developing teachers’ subject didactic competence through problem posing [J]. Educational Studies in Mathematics, 2013, 83 (1): 133-143.

[7] KOICHU B. Problem posing in the context of teaching for advanced problem solving [J]. International Journal of Educational Research, 2020 (102): 101 428.

[8] SILBER S, CAI J. Pre-service teachers’ free and structured mathematical problem posing [J]. International Journal of Mathematics Education in Science and Technology, 2017, 48 (2): 163-184.

[9] 宋运明，夏小刚，张学杰．对小学数学教科书中“提出问题”提示语编写的思考和建议——基于四种版本教科书的统计与分析[J]．课程·教材·教法，2011，31（4）：52-57．

[10] 姚一玲，徐冉冉，蔡金法．用“问题提出”诊断和评估数学教师的概念性理解[J]．数学教育学报，2019，28（4）：30-36．

[11] 中华人民共和国教育部．义务教育数学课程标准（2022年版）[M]．北京：北京师范大学出版社，2022：38-39．

[12] CAI J. U.S. and Chinese teachers’ knowing, evaluating, and constructing representations in mathematics instruction [J]. Mathematical Thinking and Learning: An International Journal, 2005, 7 (2): 135-169.

[13] CAI J. Exploring students’ conceptual understanding of the averaging algorithm [J]. School Science and Mathematics, 1998, 98 (2): 93-98.

[14] GROTH R E. Characteristics of teachers’ conversations about teaching mean, median, and mode [J]. Teaching and Teacher Education, 2009, 25 (5): 707-716.

[15] CAI J, CHEN T, LI X, et al. Exploring the impact of a problem-posing workshop on elementary school mathematics teachers’ conceptions on problem posing and lesson design [J]. International Journal of Educational Research, 2020 (102): 101 404.

[16] STAUSS S, BICHLER E. The development of children’s concepts of the arithmetic average [J]. Journal for Research in Mathematics Education, 1988, 19 (1): 64-80.

[17] CAI J. Understanding and representing the arithmetic averaging algorithm: An analysis and comparison of US and Chinese students’ responses [J]. International Journal of Mathematical Education in Science and Technology, 2000, 31 (6): 839-855.

[18] WATSON J M, MORITZ J. The longitudinal development of understanding of average [J]. Mathematical Thinking and Learning, 2000, 2 (1-2): 11-50.

[19] MOKROS J, RUSSELL S J. Children’s concepts of average and representativeness [J]. Journal for Research in Mathematics Education, 1995, 26 (1): 20-39.

[20] 宋乃庆，胡睿，蔡金法．用问题提出和问题解决测试小学生对平均数的理解[J]．数学教育学报，2020，29（3）：1-8．

[21] LIU Q, LIU J, CAI J, et al. The relationship between domain- and task-specific self-efficacy and mathematical problem posing: A large-scale study of eighth-grade students in China [J]. Education Studies in Mathematics, 2020, 105 (3): 407-431.

[22] CHRISTOU C, MOUSOULIDES N, PITTA-PANTAZI D, et al. An empirical taxonomy of problem posing processes [J]. ZDM, 2005, 37 (3): 149-158.

[23] LI X, SONG N, HWANG S, et al. Learning to teach mathematics through problem-posing: Teachers’ beliefs and performance on problem posing [J]. Educational Studies in Mathematics, 2020, 105 (3): 325-347.

[24] 张辉蓉，唐佳欣．三年级学生“数学问题提出能力”“态度”与“学业水平”关系研究[J]．数学教育学报，2023，32（1）：31-37．

[25] STICKLES P R. An analysis of secondary and middle school teachers’ mathematical problem posing [J]. Investigations in Mathematics Learning, 2011, 3 (2): 1-34.

[26] 吴骏．小学四年级学生对平均数概念理解的发展过程[J]．数学教育学报，2011，20（3）：39-41，102．

[27] CAI J, MOYER J C, WANG N, et al. Mathematical problem posing as a measure of curricular effect on students’ learning [J]. Educational Studies in Mathematics, 2013, 83 (1): 57-69.

[28] ZHANG L, CAI J, SONG N, et al. Mathematical problem posing of elementary school students: The impact of task format and its relationship to problem solving [J]. ZDM, 2022, 54 (3): 497-512.

Impact of Prompts on the Performance of Elementary School Students’ Mathematical Problem Posing Involving Arithmetic Average

CHEN Ting1, 2, SUN Qi-qi2, CAI Jin-fa3

(1. Center for Basic Education, Southwest University, Chongqing 400715, China;2. Faculty of Education, Southwest University, Chongqing 400715, China;3. The Department of Mathematics, University of Delaware, Delaware Newark 19716, USA)

Problem posing can be used as an assessment tool to diagnose students’ understanding of mathematical concepts, with problem-posing prompts also related to the diagnostic results of problem posing. To investigate the impact of prompts on elementary school students’ problem-posing performance, using average as an example, three sets of problem-posing tasks with different prompts were designed, and 262 sixth-grade students from a public elementary school were randomly selected as test subjects. The impact of the prompts on the students’ problem-posing performance was analyzed according to four aspects: quantitative scoring on posed problems, types of problems posed, difficult levels, and degree of conceptual understanding. It was found that the most of students are able to pose problems related to arithmetic averages, and the problem-posing prompts significantly affected on the content nature and difficulty of the students’ posed problems. In the more complex problem situations, the problem-posing prompts significantly affected students’ understanding of arithmetic averages.

problem posing; problem-posing prompts; arithmetic average

G623.5

A

1004–9894（2023）05–0028–07

陈婷，孙琪琪，蔡金法．引导语对小学生数学问题提出表现的影响——以平均数为例[J]．数学教育学报，2023，32（5）：28-34．

2023–08–21

国家社会科学基金“十四五”规划2022年度教育学一般课题——藏族学生数学学习行为投入测评模型构建及应用研究（BMA220221）

陈婷（1974—），女，甘肃庄浪人，教授，博士，博士生导师，主要从事民族教育、数学教育研究．蔡金法为本文通讯作者．

[责任编校：张楠、陈隽]