数学问题提出课堂教学：分析框架与应用

李欣莲，王 利，蔡金法

数学问题提出课堂教学：分析框架与应用

李欣莲1，王 利2，蔡金法3

（1．西南大学 教师教育学院，重庆 400715；2．人民教育出版社 课程教材研究所，北京 100081；3．特拉华大学 数学系，特拉华 纽瓦克 19716）

问题提出作为一种与创造力培养密切相关的认知活动，既是课程目标，也是实现该目标的途径和手段．而作为教学手段的问题提出，尽管教师能够认识其教学价值和益处，但在实践中，对于教师来说更意味着挑战和困难，这主要体现在：如何设计和实施问题提出的课堂，如何在实施了问题提出课堂教学后分析其质量和效果．为此，研究建立了问题提出教学的理论分析框架，并指明其应用方法和策略．该框架由3个维度及11个观测指标构成，其中3个维度为：（1）教师设计的问题提出任务分析；（2）教师组织学生参与问题提出活动分析；（3）教师对学生提出问题的反馈分析．实践应用结果表明，该分析框架凸显了问题提出教学的核心特征，对于分析问题提出课堂教学具有可操作性．

问题提出教学；分析框架；数学课堂教学

1 问题提出

问题提出是一项重要的认知活动，它有助于学生探索、发现和创造能力的发展，同时也有利于学生复杂问题解决能力、建模能力的提高[1-4]．为此，问题提出在教育教学改革中愈来愈彰显其独特地位．在中国课程标准中，无论是义务教育阶段或高中教育阶段的数学学科，还是物理、生物、化学等其它学科，都将培养学生发现问题、提出问题作为重要的课程目标[5-11]．同时，在呼唤拔尖创新人才培养的时代背景下，全球范围内也越来越强调问题提出的重要性．但在实际教学中，与问题解决在学校课程中的核心地位相比，问题提出的相关课程资源相对匮乏[12-13]．例如，有学者比较了不同时期的两版小学数学教材中问题提出的内容，发现其内容有所增加，但整体上还较少[14]．因此，作为课程实施者，教师若想设计和开展问题提出教学则需要额外投入精力，成为课程的再设计者[15]．

为了能成为合格问题提出课程再设计者，教师首先需要学习相关知识，增强自身问题提出的能力和预测学生可能的提出问题的能力；其次，需要改变固有的教学观念，认识到问题提出的教育价值；最后，在行动层面尝试将问题提出融入到日常教学中．在具体实施中，教师大多停留在对问题提出教育价值的观念认同上，在行动上还存在着诸多困难．从一项旨在帮助教师学习使用问题提出教学的主题学习活动中发现，他们在问题提出知识和信念方面有明显的改变，但在行动方面的改变不如预期[16]．其原因有二：一是对进行问题提出的教学设计存在困难[17]；二是难以评估怎样的问题提出课堂教学是合格的、有效的．这不仅影响了整体的课堂教学质量，也不利于教师实施这一新教学方法后自我效能感的提高．

为解决教师在问题提出教学实施过程中存在的困难，建立一个问题提出教学分析框架尤为重要．一方面，教师可以参考该框架进行规范化的问题提出教学实施；另一方面，教师在开展了问题提出课堂教学后可依据该框架进行教学反思和改进．为此，研究基于已有文献建立问题提出课堂的理论分析框架，并指明其应用方法和策略，以期从理论层面和实践层面解决教师在开展问题提出教学时存在的困惑，推动问题提出在课堂中的落实，实现问题提出应有的教育价值．

2 数学问题提出课堂教学分析框架的建构

整合问题提出的数学课堂和常规问题解决的数学课堂最典型的区别在于数学问题提出任务的设计和使用[18]．根据前期研究成果，整合问题提出活动的课堂一般包括以下教学过程：教师根据教学目标设置不同类型的问题并提出任务情境、教师提出任务要求、学生参与问题提出活动、师生处理所提问题[19-23]．因此，从教师视角设计、实施和反思问题提出课堂教学有3个关键方面：教师设计问题提出任务—教师组织学生参与问题提出活动—教师对学生提出的问题进行反馈．其它关于问题提出教学的研究也在不同程度上凸显其中的一方面或者多个方面[24-27]．下文将围绕这3个关键维度，尝试进一步论述其在二级操作层面如何开展．

（1）维度一：教师设计的问题提出任务分析．

问题提出任务设计是问题提出课堂教学的起点[28]．该任务是一种情境平台（包括日常生活的情境、数学表达式、图表等），以支持学生开展问题提出活动．然而，对许多教师而言，设计规范的问题提出任务是一项重大挑战[17]．其原因是教师对问题提出涵义的理解存在偏差，不能正确区分问题提出、学生质疑、教师提问等相关概念[29]，以至于设计的任务不恰当，把学生质疑、教师提问等任务当作是问题提出任务．这3种任务之间的差异在于：课堂中的问题提出是指教师要求学生根据给定的问题提出任务情境，提出可解答的数学问题，属于教师设置的一种教学任务；学生质疑是课堂提问中师生互动的一部分，可不作为教学任务；而课堂教师提问主要指教师提供一个问题，要求学生回答，并不要求学生提出问题．因此，深刻理解问题提出的内涵，设计恰当的问题提出任务是开展问题提出教学的前提和基础．

在问题提出任务类型选择上，存在3种典型类型可供选择，包括：（1）数学表达式类任务；（2）现实情境类任务；（3）数学模式、图形、表格类任务．不同类型的问题提出任务有不同的作用和特点，教师应根据不同知识内容的特点，设置不同类型的、恰当的问题情境．一般而言：（1）数学表达式作为一种情境，对结构有着较强的限制，学生所提问题会较为集中，易于进行教学处理．（2）现实情境与学生的生活实际最为贴近，因此学生易于理解和接受．这种情境可以帮助学生感受到数学的应用价值，从而更容易激发他们对数学学习的兴趣．（3）数学模式、图形、表格等情境中，模式情境较为常见，适用于数学规律的教学；图形情境适用于几何内容；表格适用于统计方面的教学[30]．一般而言，多样的问题提出任务类型更有助于调动学生的学习积极性．

确定了问题提出任务的情境后，教师需考虑对学生所提问题的数量及难度的要求，进行引导语设计，呈现问题提出情境之后，教师伴随怎样的引导语，直接影响学生的问题提出表现[31-33]．Cai和Jiang区分了4种不同的问题提出引导语：（1）根据给定的算式提出一个问题；（2）根据同样的数学关系提出不同的问题；（3）根据已知条件，仿照给出的问题，提出其它问题；（4）根据条件，提出尽量多的问题[13]．不同类型引导语下，学生获得的学习机会存在差异．典型地，对于同一个问题提出任务情境，要求学生提出一个问题和提出不同难度的问题，以及提出尽可能多的问题对学生的挑战迥异．因此，教师可根据实际需要选择不同的引导语，如提出一个问题，提出不同难度的问题，提出尽可能多的问题，提出问题挑战你的同学或教师等．

教师根据所教内容确定了问题提出任务之后，需要考虑该任务的功能性，即服务于课堂教学目标的达成．按照课堂中数学任务出现的不同时间及达成的不同教学目标[34]，可以将问题提出任务分为3类：复习型任务、学习型任务和练习型任务．在课堂的起始和结束阶段，将问题提出作为复习型和练习型任务对原有的课堂教学形态不会造成太大冲击，然而这类方式对于发挥问题提出教学的优势比较有限．更优的状态是，教师能够逐步尝试将问题提出任务设计为学习型任务，使之与教学目标之间的关系更为紧密，为学生营造探究、联系和创造的学习环境[35]．

以上4个子维度的考察可以通过表1来完成，并可用数值表示类型以简化形式．

（2）维度二：教师组织学生参与问题提出活动分析．

教师组织学生参与问题提出活动是问题提出课堂教学实施的关键．首先，需要考虑学生参与问题提出活动的组织形式——小组合作或个别完成．问题提出教学既可以体现学生数学学习的个体性也可以体现社会性[23]．问题提出任务更具有开放性，可为学生开展小组合作学习提供较好的平台，构建学生学习共同体，体现了数学学习的社会建构性．而学生独立思考完成，这种组织形式在教学中也经常被教师采用，它体现了数学学习的个体建构性．

其次，学生成功理解问题提出任务情境及任务要求是学生顺利参与问题提出活动的前提，因此教师需要通过全班询问、小组询问或个别询问的形式了解学生是否很好理解了问题提出任务及要求．若学生对情境或要求存疑，教师需再次阐释直至学生完全理解．

此外，还需考虑教师提示的时机．根据Stein等的研究，高水平的数学任务不一定能直接导致高水平的课堂教学，因为教师在实施数学任务的过程中不一定维持高水平的实施，他们可能会通过不恰当的提示降低任务的难度水平[36]．类似地，在实施问题提出任务时，如果学生还未充分思考教师就立即给出很强的提示，其难度会大大降低，甚至会变成对示例的模仿，从而降低甚至失去其学习价值．因此，在呈现问题提出任务后，教师是否在学生未开始思考之时就给予明确的提示以降低学生进行问题提出活动的难度是影响问题提出任务实施水平的重要因素．但若是在学生经过相当的思考和挣扎之后仍然有困难则另当别论，两者的区别在于学生是否经历必要的独立思考和“挣扎”．

以上3方面的考察可以通过表2来完成，并可用数值表示类型以简化形式．

表1 教师设计的问题提出任务分析

注:此表中问题提出的任务数量可根据教学实际增减．

表2 教师组织学生参与问题提出活动分析

注:此表中问题提出的任务数量可根据教学实际增减．

（3）维度三：教师对学生提出问题的反馈分析．

教师对学生提出的问题进行反馈是问题提出课堂教学实施的重要保障，这无疑对教师提出了较大的挑战．研究表明，当学生被要求参与问题提出活动时会有各种不同的表现，可能提出非数学问题、不可解的数学问题，也可能提出可解答的数学问题、复杂的数学问题等[32]．而可解答的数学问题的质量也有待进一步提高[37-39]．因此，学生提出问题以后，教师首先需要对学生提出的问题进行分析和梳理．对于那些非数学问题、非可解的数学问题或存在歧义的数学问题要及时指出，以帮助学生逐步学会提出清晰的数学问题，进而提出更高认知要求、更具多样化表征、更具开放性、包含更多数学概念的、更有价值的数学问题．

问题提出任务的开放性及学生思维的多样性特点决定了问题提出课堂上学生会提出各式各样的问题，这也是问题提出教学让教师生畏的重要因素之一．面对众多的问题教师如何挑选，这对教师来说无疑是一个重大挑战．方法之一是教师在课前预设学生可能提出的问题类型[40]，迅速将学生提出的问题进行归类整理．在此过程中依据当堂课的教学目标及问题的难度选择一些典型问题进行解答．目前可借鉴的经验为：对于与当堂课教学目标不相关的问题进行忽略，并向学生解释忽略的原因；对于与当堂课教学目标相关的问题则分为3种情况，若是简单问题则可以以简单形式快速解答，若是难度较大、需要花费较多时间的问题则可布置成作业供学生课后思考和解答，而对于中等难度的问题教师则可以在课堂上重点分析、讨论、探究解答[18]．在此过程中，问题提出可诊断学生概念理解水平的工具价值得以发挥．通过对学生提问的整理，教师可以适时了解学生的学习情况，从而调整自己的教学行为，开展更为精准的教学．挑选部分学生提出的问题进行解答是问题提出教学必不可少的方面，即实现问题提出与问题解决之间的整合．

以上方面的考察可以通过表3来完成，可形成教师对学生提出问题的反馈分析表．

表3 教师对学生提出问题的反馈分析

注:此表中问题提出的任务数量可根据教学实际增减．

3 数学问题提出课堂教学分析框架的应用

为了检验上述问题提出课堂教学分析框架的实用性，需结合实际问题提出教学课堂案例进行分析与说明．研究选择的案例来自一项旨在帮助教师学习使用问题提出教学法的工作坊，关于工作坊的详细描述可参考文献[16]和[41]．其中，第四期工作坊的主要内容为问题提出教学案例观摩与研讨，共有6位连续参加了4期工作坊的教师展示．这6位教师各自分享了一个课堂教学录像，这些录像的内容为他们自主设计并实施的、融入了问题提出教学方法的课堂．研究选择其中一节由L教师执教的案例．选择这一案例原因有二：一是，成功融入了问题提出，受到工作坊领衔专家的认可；二是，存在的一些不足，对于初学用问题提出进行教学的教师而言具有相当的典型性．L教师是一名新手教师，教龄在5年以下，所在学校在学区内属于优质学校．课例的学习主题为“用字母表示数”，属于“简易方程”单元的起始课．案例设定的知识目标为：让学生理解并掌握用含有字母的式子表示简单的数量、数量关系和公式等．

3.1 教师设计的问题提出任务分析

能够设计出规范的问题提出任务是教师开展问题提出教学的第一个挑战．在进行问题提出教学分析时首先需要识别出教师自认为的问题提出任务，对其规范性进行辨别．该课例中教师报告设计了3个问题提出任务，其分析见表4．

表4 案例中教师设计的问题提出任务分析

注:“-”表示不适用．

该课例中教师自我报告试图发起3次问题提出活动：3′00″—04′23″，33′30″—35′19″和35′30″—42′33″．3个问题提出任务中，第一个任务并不是一个规范的问题提出任务，原因在于教师并未向学生提供一个可以提出可解决数学问题的情境，而只是一个提问，学生针对这一提问的回答只是他们的疑问．如有学生回答：“用什么字母来表示数呢？”“字母如何表示数？”等等．诚然这些来自学生的疑问也具有促进学生思考的功能，但这些疑问并非可供解决的数学问题．而另外两个任务则是规范的问题提出任务，属于数学表达式类问题提出任务，教师给出含有字母的式子，要求学生提出一个能用该式子解答的数学问题．学生给出的回答则是提出可解决的问题，例如：“小明有颗糖，小东的糖是小明糖的6倍，请问小东有多少颗糖？”表达式的复杂度呈现递增状态，有利于学生循序渐进开展问题提出的学习活动．

从两个问题提出任务出现的位置及课件呈现的信息可以判定，其所承担的任务功能为帮助学生巩固和深化所学知识，均为练习型任务．特别是第三个问题提出任务，教师设计了导学案，并提供给学生独立思考完成的时间，学生的参与度和积极性都较高．

3.2 教师组织学生参与问题提出活动分析

通过维度一的分析，排除了不规范的问题提出任务，下面仅针对规范问题提出任务进行教师引导的分析，见表5．

表5 案例中教师组织学生参与问题提出活动分析

任务的组织形式方面，第二个问题提出任务中，教师呈现任务之后立即让学生举手作答，没有给予学生等待的时间．而在第三个问题提出任务中，教师首先要求学生先在导学案上独立作答，再进行小组（前后桌4人）交流，互相判断对方所提问题是否符合要求，最后选择了第四小组的4名同学上台讲演展示所提出的问题，并引导台下的同学判断所展示问题是否表达清晰，符合要求．

教师诊断方面，第二个任务的数学表达式6，教师通过抽点学生上台写出它的不同形式以了解学生是否理解了任务情境．第三个任务中，教师在全班巡回的过程中，通过一对一交流，帮助学生正确理解了任务情境．

提示时机方面，在第二个问题提出任务中，教师任务情境简单，不少学生可以直接举手回答，并未进行提示；第三个任务中，教师在全班巡视后，发现部分同学存在困难，于是进行了如下提示：“同学们，老师来作一个示范，橡皮擦的价格是元，你买了8个，你买了5个，请问一共花了多少钱，可不可以？这是老师给你们提供的一个思路，好，你们继续写．”

3.3 教师对学生提出问题的反馈分析

类似地，在前两个阶段分析的基础上，对每个问题提出任务下学生提出问题的反馈从4方面进行逐个分析，以了解教师在给予学生问题提出反馈方面的表现，详见表6．

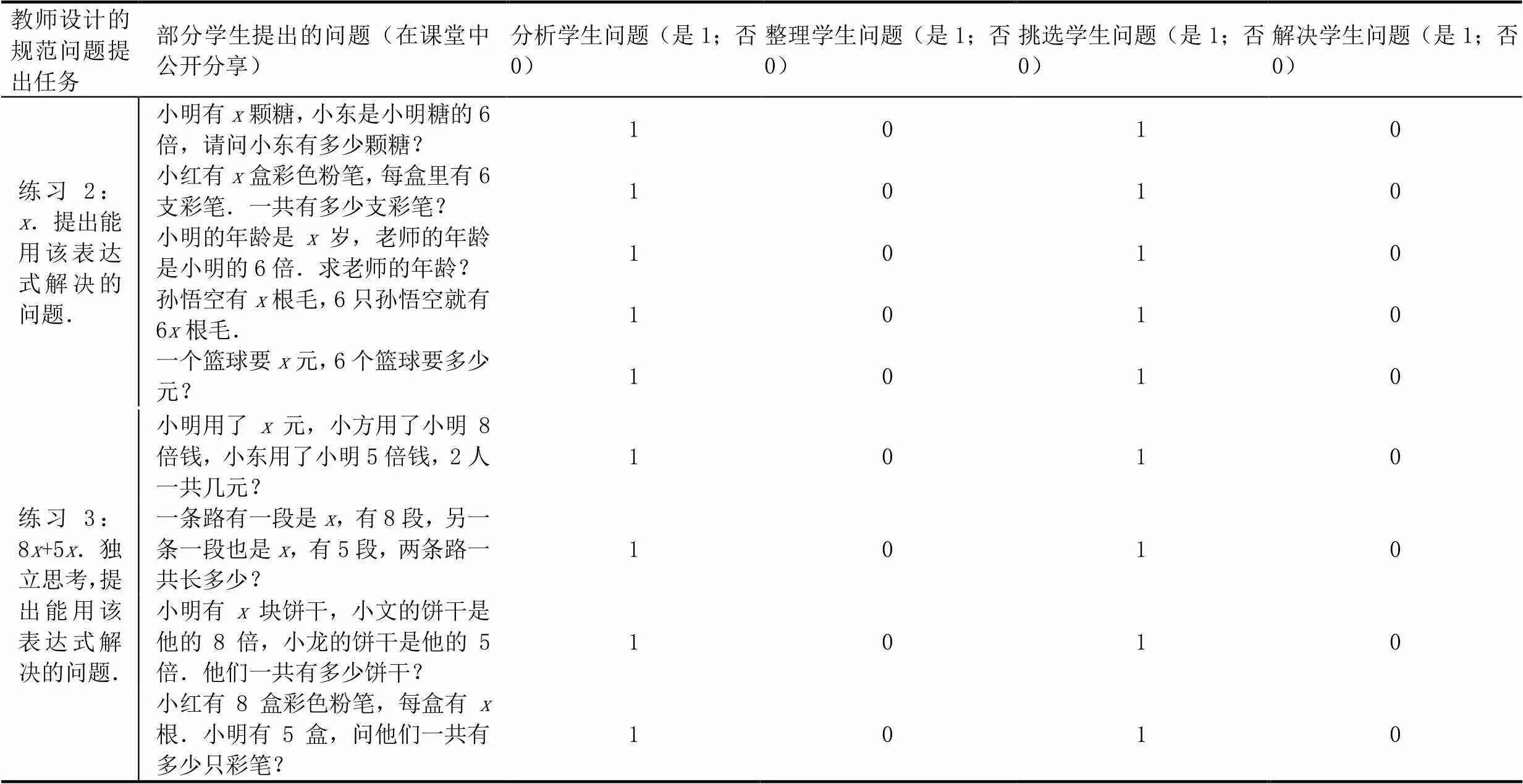
表6 案例中教师对学生提出问题的反馈分析

对于第二个问题提出任务，教师挑选了5名同学分享了他们提出的问题，其中前两个问题存在语言表达不清晰的问题，但是教师未直接反馈，而是通过联系其他同学判断所提问题是否可以用给定算式解决．其余问题教师均通过提问分析所提问题是否清晰和可解，能否用给定的算式解答等，如第四个答案，学生所提问题为一个陈述表达，教师给予相应的纠正．对于第三个问题提出任务，教师挑选了第四小组的4名同学分享他们的问题，并对问题的清晰度全部给予指导．例如，对于第一和第三个问题，提醒学生要明确“2人”“他们”具体指代的是谁？而对第二个问题，则强调需要补充上单位信息．同时，该教师注重引导其他学生参与对所分享问题的分析中．例如，对第四个问题的讨论，师生之间开展了如下对话，营造了良好的学习氛围．

师：大家看她这个问题能不能用这个表达式解决？

台下生1（举手）:不能，因为她没有说小明的彩笔和小红的彩笔是一样的，要加上小明有同样的5盒彩笔才行．

师：同不同意．

全班：同意．

师：我们提出的问题信息表达要准确，好谢谢你．

课例中教师选用的问题提出任务为数学表达式类且只要求学生提出一个问题，学生所提问题比较集中，因此教师挑选了9名同学全班分享他们的答案，但并未观察到教师对学生所提问题进行分类整理，也未选择其中的问题进行进一步的解答．

4 结论与建议

4.1 数学问题提出教学分析框架及其适用性与研究展望

研究从理论层面构建了3维度11观测指标的数学问题提出课堂教学分析框架．其中3个一级维度：教师设计的问题提出任务分析—教师引导学生参与问题提出活动分析—教师对学生提出问题的反馈分析及11个观测指标，均可较好应用于实际问题提出课堂案例的分析中，凸显了问题提出教学的核心特征．同时在实际应用中也发现，某些二级观测指标的选择和应用会受到教师所设计的问题提出任务类型的影响，需要根据任务特点进行适当地选择．

在实践层面，该框架可以在不同阶段指导教师开展问题提出课堂教学．课前，教师可以参照3维度11观测指标进行问题提出课堂教学设计，预设教学过程；课中，教师可以结合框架实施、调整自己的课堂活动，使其取得更好的教学效果；课后，教师可以运用该框架对课堂中发生的教学活动进行再分析和反思，以进一步修正课前的教学设计，从而实现教学改进．此外，该框架除了服务于教师个人的专业成长，也可以用于集体的教研活动中，例如，开展问题提出教学课例观察、研讨，问题提出教学案例的开发、设计等．

需要指出的是，目前由于对如何有效开展问题提出教学的研究比较欠缺，取得良好教学效果的问题提出教学案例也处于积累阶段[18，23]．某些问题尚不完全明确，如除了表1中列举的任务要求引导语外，还有哪些可行的引导语；不同教师如何凭借自身的教学经验挑选学生提出的问题；如何把问题提出阶段学生提出的问题延续到下一阶段的问题解决，实现问题提出与问题解决的衔接等．因此，框架还需要结合进一步的研究成果以及更加丰富的问题提出教学案例进行优化，尤其是更加细化二级观测指标的内容，从而进一步提高其指导性．

4.2 教师设计实施数学问题提出课堂教学的建议

（1）问题提出任务选择和设计方面．

设计问题提出教学，教师首先需要正确理解问题提出的内涵，区别其易混淆概念，并且提升自身问题提出的能力以及预测学生可能提出问题的能力．其次，需要结合学生的学习目标与学生学习基础设置恰当的问题提出情境[20]．问题提出任务的选择宜多样，为学生提供充分的情境平台，使得学生的问题提出活动更加自然而深刻地发生．教师在对学生问题提出任务数量及难度方面的要求可以尽量丰富，留给学生更多的学习空间．对于小学低年级以外的学生，不仅让他们提出一个问题，而是鼓励他们提出多个不同难度的问题．

在教师开始学习将问题提出整合于课堂教学时，将问题提出任务设置为练习型任务是一种比较基础、安全的处理方式，对原本的课堂教学形态影响较小，同时也在一定程度上增加了学生提出问题的机会．但是在积累了相当问题提出经验之后，教师有必要尝试将问题提出设置为学习型任务，便于取得更加突出的教学效果．如特级教师丁老师[42]曾获全国讲课比赛一等奖的课例，就很好地应用问题提出任务于新知识的学习中，并取得非常好的学习效果；骨干教师裴老师也成功将问题提出任务设置为学习型任务，并取得良好教学效果[43]．

（2）问题提出活动组织方面．

组织实施的形式可以多种多样，结合问题提出任务的难度，对于简单的任务可以在学生独立思考后让学生举手作答，并通过教师反馈将个别学生的答案和其他同学的思考进行连接．对于有一定难度的任务则可以先提供给学生更多的独自思考时间，再进行小组讨论或者全班讨论，在时间允许的情况下可进行全班的展示．学生充分理解问题提出任务情境及要求是顺利参与问题提出活动的前提，教师可通过全体提问、个别指导等形式诊断其对任务的理解情况．

教师在组织学生参与问题提出活动时需注意保持任务的难度水平，让学生有机会经历思维的“挣扎”过程，而不急于进行问题提出示范从而降低学生提问的难度．但这并不意味着教师完全不能给予提示，若学生在经历充分的思考之后仍然无法进行，此时教师可以提供帮助．常用的方法包括：第一，教师示范性提出一个问题，诸如上述案例中教师的做法；第二，教师可以告知学生一些常用的提出问题的策略：如否定假设法（what if not），即先对情境中的已知条件进行分析，改变这些条件的一个或多个提出新的数学问题[44]；第三，告知学生提出问题的一般步骤[25]：理解目标情境—设计问题背景—形成问题表述—解决提出的问题—评估—回顾总结等．

（3）教师对学生提出问题的反馈方面．

学生经历了自主提出问题的课堂活动之后，教师需要对学生提出问题进行分析、梳理，在此过程中了解学生的思维水平，对所学内容的掌握状态．一般而言，学生能够提出可解决的问题，但他们提出问题的水平需要进一步提高．通过课堂对话，教师可以有意识引导学生提出多样、新颖、更具挑战性、包含更多概念理解及表征的问题，真正将培养学生“四能”落实于课堂教学之中．

在此基础上，教师进一步挑选部分学生提出的问题以进一步解决，实现问题提出与问题解决的融合．而如何挑选，挑选哪些问题以及如何安排解决的顺序，主要依赖于教师的教学经验以及课前的预设．虽然研究介绍了一种可借鉴的经验，然而还有哪些经验，哪种经验更优仍待进一步的研究．最后需要指出的是，在进行问题提出课堂教学分析时，比较好的形式是进行课堂视频的录制，其具有易于保存，可反复观看、分析的优点，也可以作为集体教学研讨时的素材．相对于课堂实录，也能更多反映出课堂教学生动丰富的细节．

[1] AYVAZ Ü, DURMUŞ S. Fostering mathematical creativity with problem posing activities: An action research with gifted students [J]. Thinking Skills and Creativity, 2021 (40): 100 846.

[2] HARTMANN L M, KRAWITZ J, SCHUKAJLOW S. Create your own problem! When given descriptions of real-world situations, do students pose and solve modelling problems [J]. ZDM, 2021, 53 (4): 919-935.

[3] JUNG H, MAGIERA M T. Connecting mathematical modeling and social justice through problem posing [J]. Mathematical Thinking and Learning, 2023, 25 (2): 232-251.

[4] XIE J, MASINGILA J O. Examining interactions between problem posing and problem solving with prospective primary teachers: A case of using fractions [J]. Educational Studies in Mathematics, 2017, 96 (1): 101–118.

[5] 中华人民共和国教育部．义务教育数学课程标准（2022年版）[M]．北京：北京师范大学出版社，2022：5-6．

[6] 中华人民共和国教育部．义务教育生物课程标准（2022年版）[M]．北京：北京师范大学出版社，2022：6-7．

[7] 中华人民共和国教育部．义务教育物理课程标准（2022年版）[M]．北京：北京师范大学出版社，2022：4-5．

[8] 中华人民共和国教育部．普通高中数学课程标准（2017年版2020年修订）[M]．北京：人民教育出版社，2020：7-8．

[9] 中华人民共和国教育部．普通高中化学课程标准（2017年版2020年修订）[M]．北京：人民教育出版社，2020：3-4．

[10] 中华人民共和国教育部．普通高中生物课程标准（2017年版2020年修订）[M]．北京：人民教育出版社，2020：1-2．

[11] 中华人民共和国教育部．普通高中物理课程标准（2017年版2020年修订）[M]．北京：人民教育出版社，2020：4-5．

[12] JIA S, YAO Y. 70 years of problem posing in Chinese primary mathematics textbooks [J]. ZDM, 2021, 53 (4): 951-960.

[13] CAI J, JIANG C. An analysis of problem-posing tasks in Chinese and US elementary mathematics textbooks [J]. International Journal of Science and Mathematics Education, 2017 (15): 1 521-1 540.

[14] 胡典顺，蔡金法，聂必凯．数学问题提出与课程演变：两个版本小学数学教材的比较[J]．课程·教材·教法，2015，35（7）：75-79．

[15] CAI J, HWANG S. Teachers as designers of curriculum to teach mathematics through problem posing: Conceptualization and initial findings of a problem-posing project [J]. ZDM, 2021, 53 (6): 1 403-1 416.

[16] CAI J, CHEN T, LI X, et al. Exploring the impact of a problem-posing workshop on elementary school mathematics teachers’ conceptions on problem posing and lesson design [J]. International Journal of Educational Research, 2020 (102): 101 404.

[17] 宋乃庆，周莞婷，陈婷，等．小学数学教师“问题提出”的教学信念研究[J]．数学教育学报，2019，28（4）：24-29．

[18] ZHANG H, CAI J. Teaching mathematics through problem posing: Insights from an analysis of teaching cases [J]. ZDM, 2021, 53 (4): 961-973.

[19] LI X, SUN X, CAI J. Integrating problem posing into the mathematics classroom: Current advances and future directions of research [J]. Current Opinion in Behavioral Sciences, 2022 (48): 101 213.

[20] 徐冉冉，李丹杨，姚一玲，等．指向教学改进的“问题提出”数学教学[J]．数学教学，2020（10）：1-8．

[21] CAI J. What research says about teaching mathematics through problem posing [J]. Éducation & Didactique, 2022, 16 (3): 31-50.

[22] 莫延安，王涛．小学数学“问题提出”教学步骤解读[J]．教育研究与评论（小学教育教学），2023（2）：59-66．

[23] 蔡金法，姚一玲．数学“问题提出”教学的理论基础和实践研究[J]．数学教育学报，2019，28（4）：6．

[24] 张辉蓉，冉彦桃，刘蝶，等．教师“问题提出”教学知识建构[J]．数学教育学报，2019，28（2）：13-17．

[25] ÖRNEK T, SOYLU Y. A model design to be used in teaching problem posing to develop problem-posing skills [J]. Thinking Skills and Creativity, 2021 (41): 100 905.

[26] ERKAN B, KAR T. Pre-service mathematics teachers’ problem-formulation processes: Development of the revised active learning framework [J]. The Journal of Mathematical Behavior, 2021 (65): 100 918.

[27] ELLERTON N F. Engaging pre-service middle-school teacher-education students in mathematical problem posing: Development of an active learning framework [J]. Educational Studies in Mathematics, 2013 (83): 87-101.

[28] 陈婷，徐红，徐冉冉，等．数学教师学习使用“问题提出”教学法的个案研究——以“用字母表示稍复杂的数量关系”为例[J]．数学教育学报，2019，28（2）：7-12．

[29] 许天来，蔡金法．数学课堂中的问题提出与教师提问、学生质疑的联系和区别[J]．小学教学（数学版），2019（12）：19-23．

[30] 蔡金法，许天来．数学问题提出的例子、类型和内涵[J]．小学教学（数学版），2019（Z1）：34-40．

[31] CAI J, HWANG S. Generalized and generative thinking in US and Chinese students’ mathematical problem solving and problem posing [J]. The Journal of Mathematical Behavior, 2002 (21): 401-421.

[32] SILVER E A, CAI J. An analysis of arithmetic problem posing by middle school students [J]. Journal for Research in Mathematics Education, 1996, 27 (5): 521-539.

[33] 许天来，蔡金法．美国数学课程中的“问题提出”——期望与挑战[J]．数学教育学报，2019，28（2）：18-23．

[34] 邵珍红．中美初中课堂中数学任务特征的比较研究[J]．比较教育研究，2015（2）：102-107．

[35] 张玲，宋乃庆，蔡金法．问题提出：基本蕴涵与教育价值[J]．中国电化教育，2019（12）：31-39．

[36] STEIN M K, GROVER B W, HENNINGSEN M. Building student capacity for mathematical thinking and reasoning: An analysis of mathematical tasks used in reform classrooms [J]. American Educational Research Journal, 1996, 33 (2): 455-488.

[37] PALMÉR H, VAN BOMMEL J. Young students posing problem-solving tasks: What does posing a similar task imply to students [J]. ZDM, 2020, 52 (4): 743-752.

[38] GUO Y, YAN J, MEN T. Chinese junior high school students’ mathematical problem-posing performance [J]. ZDM, 2021, 53 (4): 905-917.

[39] XU B, LI M. Chinese eighth graders’ competencies in mathematical problem-posing [M] // XU B, ZHU Y, LU X, et al. Beyond Shanghai and PISA: Cognitive and non-cognitive competencies of Chinese students in mathematics. Berlin: Springer, 2021: 67-86.

[40] XU B, CAI J, LIU Q, et al. Teachers’ predictions of students’ mathematical thinking related to problem posing [J]. International Journal of Educational Research, 2020 (102): 101 427.

[41] LI X, SONG N, HWANG S, et al. Learning to teach mathematics through problem posing: Teachers’ beliefs and performance on problem posing [J]. Educational Studies in Mathematics, 2020, 105 (3): 325-347.

[42] 丁玉华，曾令鹏．“乘法分配律”教学实录与评析[J]．小学数学教育，2017（21）：43-46．

[43] 徐冉冉，裘晓丽，姚一玲，等．基于教师—研究者伙伴关系的初中数学教学改进——以“一次函数”“问题提出教学”为例[J]．数学教育学报，2021，30（1）：25-31．

[44] BROWN S I, WALTER M I. The art of problem posing [M]. Hillsdale: Lawrence Erlbaum Associates, 2005: 24.

Analysis of Problem-Posing Teaching in the Classroom: A Framework and Its Application

LI Xin-lian1, WANG Li2, CAI Jin-fa3

(1. School of Teacher Education, Southwest University, Chongqing 400715, China;2. Curriculum and Teaching Materials Research Institution, People’s Education Press, Beijing 100081, China;3. The Department of Mathematics, University of Delaware, Delaware Newark 19716, USA)

As a cognitive activity related to the cultivation of creativity, problem posing is not only a curriculum goal but also a teaching method to achieve that goal. As a teaching method, although teachers can recognize its value and benefits, they are also full of concerns about its challenges and difficulties. The core challenge is how to design and implement problem-posing teaching in the classroom as well as how to judge the quality and effects of a problem-posing lesson. To address these challenges, this study builds a theoretical analyzing framework for classrooms integrating problem posing. The framework consists of three dimensions and eleven observation indicators. The three dimensions include: (1) analyzing designed problem-posing tasks; (2) analyzing how the teacher integrates students into problems-posing activities; and (3) analyzing the teacher’s feedback after students pose problems. The results of applying this framework to a typical class case using problem posing indicate that the framework highlights the core characteristics of problem-posing teaching and works well for analyzing classroom teaching that incorporates problem posing.

teaching with problem posing; analyzing framework; mathematical classroom teaching

G623.5

A

1004–9894（2023）05–0021–07

李欣莲，王利，蔡金法．数学问题提出课堂教学：分析框架与应用[J]．数学教育学报，2023，32（5）：21-27．

2023–08–21

全国教育科学“十三五”规划2020年度教育部青年项目——小学生问题提出能力及其关键影响因素的测评工具研究（EHA200404）；西南大学引进人才计划项目（SWU118118）

李欣莲（1989—），女，四川雅安人，讲师，博士，主要从事数学课程与教学研究．蔡金法为本文通讯作者．

[责任编校：张楠、陈汉君]