立磨成品粒度与操作参数的关系研究

王利辉

1洛阳矿山机械工程设计研究院有限责任公司 河南洛阳 471039

2智能矿山重型装备全国重点实验室 河南洛阳 471039

立 式辊磨简称立磨，采用料床粉磨机理，通过磨辊与磨盘的相对运动粉磨物料，集破碎、研磨、烘干及分选等工序于一体，流程简单，粉磨效率高，现已广泛用于生料、水泥和矿渣等的粉磨[1]。未来，立磨将在越来越多的领域得到应用，而不同应用领域对立磨成品粒度有不同的要求，对立磨成品颗粒的分布特性提出了更严苛的要求。因此，立磨设计者，有必要探索研究立磨成品粒度分布特征与操作参数之间的关系，实现精准控制。笔者利用 LGM/LGMS 380 立磨试验台进行试验并对数据进行回归分析，研究立磨成品粒度分布特征与操作参数之间的关系。

1 粉磨试验

LGM/LGMS380 立磨试验台的结构和参数见文献 [2-3]。笔者认为，立磨系统成品的粒径特征首先是由粉磨系统决定的，而选粉机只是对粉磨系统产品进一步分选。为了简化问题，采用开路试验，即粉磨系统工作，选粉和收尘系统不工作。

试验以钛渣作原料，将原料破碎并筛选至一定的粒度，装入进料仓备用。开启主电动机，喂料至一定料层厚度，降辊并给磨辊施加一定的加载力进行物料粉磨。物料经研磨后，在离心力作用下，直接从磨盘周边的喷嘴环溢出，由磨盘下的排渣口排出。试验立磨每一运行状态稳定之后，间隔一定时间在排渣口处取样。取样时，记录加载磨盘转速、液压缸压力、料层厚度等操作数据，对样品进行粒度分布检测并记录。调整不同的操作参数，并记录其对应的产品粒度分布数据[2]30。试验共做了 10 组，结果如表1 所列。

表1 试验结果Tab.1 Test results

据相关研究，微粉碎产品粒径分布具有曲线右歪斜形状，但如果横坐标不采用粒径，而是采用粒径的对数，这时分布曲线将成正态分布[4]。因此，笔者将上表中的网目转化为组中值，并计算出其相应的对数值，将筛下累积值转化为分布频率，并将加载液压缸压力转化为磨辊投影面积压力，得到结果如表2、3 所列。

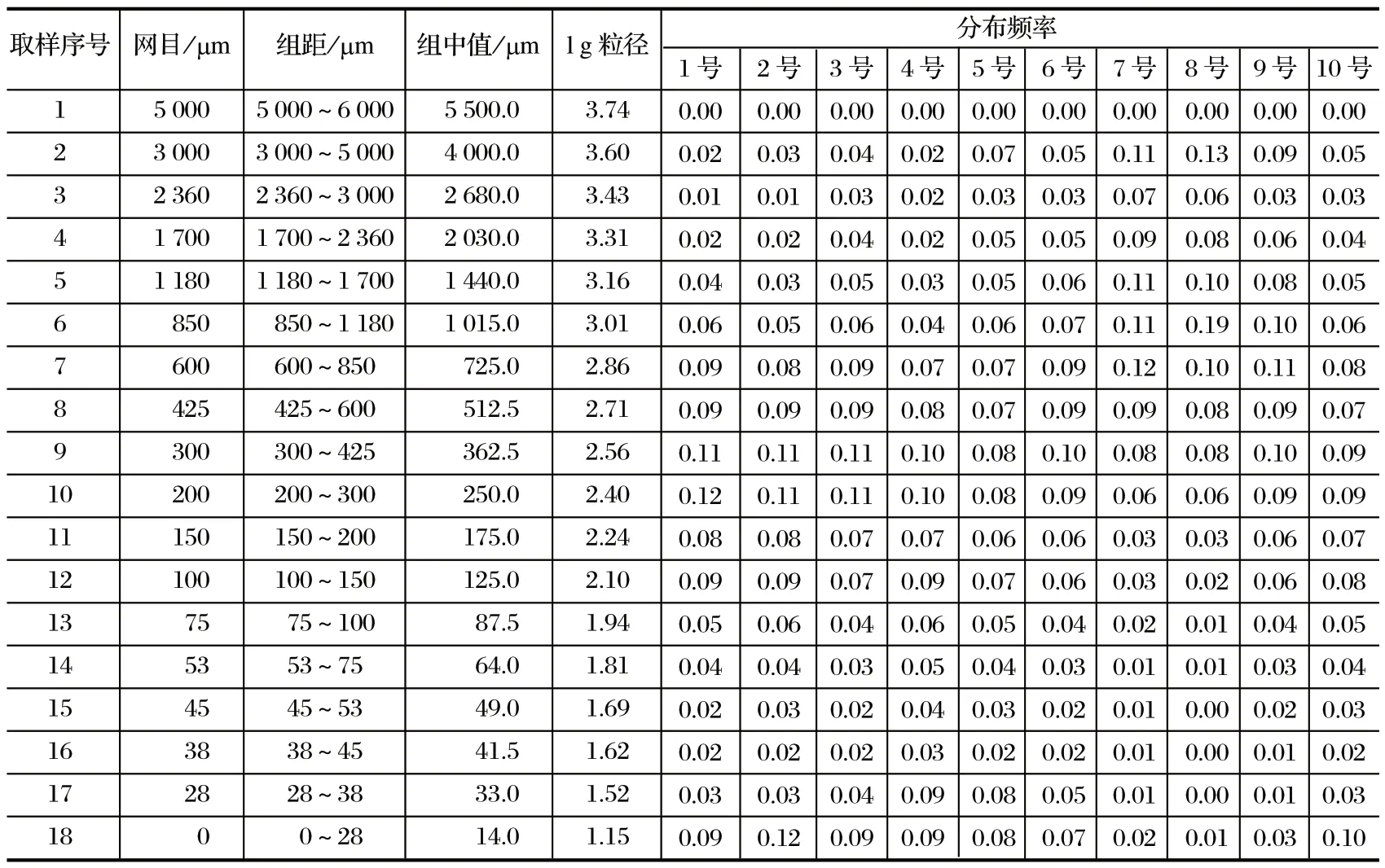
表2 转化后数据 1Tab.2 Converted data 1

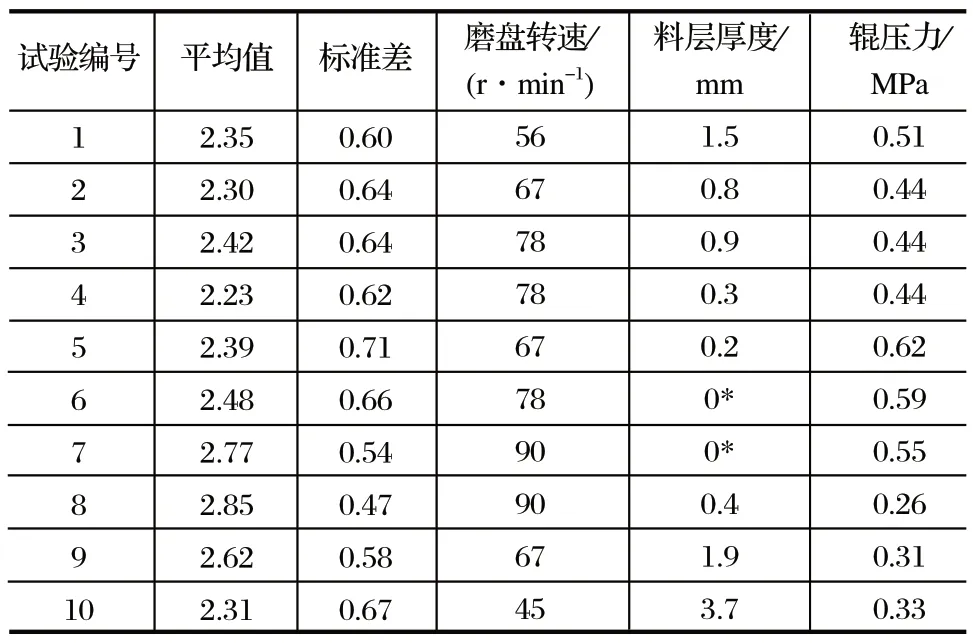
表3 转化后数据 2Tab.3 Converted data 2

估算每组样品的粒径对数的平均值

粒径对数的标准差

式中：n为每组样品的取样测量个数，取值为 18；k为某组样品中的取样序号，1～n；xk为某组样品中第k个取样测量的粒径的对数；pk为某组样品中第k个取样的分布频率。

2 回归分析

由正态分布概率密度函数可知，如果已知一组数据正态分布概率密度函数中的平均值与标准差，就可以完全确定这组数据的分布特征。对于本试验来说，如果能够找到立磨粉磨成品粒径对数平均值和标准差与相关操作参数的关系，就可以通过调整相关操作参数来精确控制成品的粒径分布。

与粉磨成品粒径对数平均值和标准差有关的操作参数是磨盘转速n、料层厚度h和辊压力pa。其中，磨盘转速决定了物料在磨盘上停留的时间，如果磨盘转速过快，物料在离心力作用下将很快脱离磨盘进入成品区，而得不到充分粉磨；如果磨盘转速过慢，物料在磨盘停留时间过长，将导致过粉磨。料层厚度由喂料量、磨盘转速和辊压力共同决定，在磨盘转速和辊压力一定的情况下，喂料量是主要的影响因素。辊压力既影响料层厚度，也影响粉磨成品的性质。因此，有以下函数：

2.1 关于成品粒径对数平均值的回归计算

利用 Stata 软件，用磨机成品粒径对数的平均值与磨盘转速、料层厚度、辊压力的对数以及磨盘转速、料层厚度、辊压力的平方做回归计算，得到的结果如表4 所列。

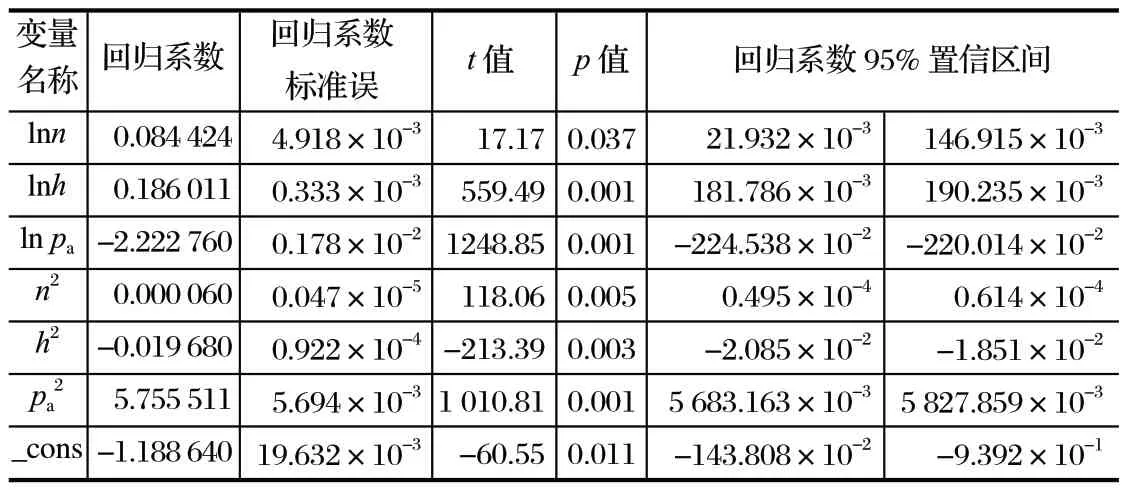
表4 回归计算结果 1Tab.4 Regression calculation result 1

由此可知，成品粒径对数平均值与磨盘转速、料层厚度和辊压力的回归方程如下：

方程的p值 ＜ 0.01，说明回归方程整体显著。方程 (5) 中，所有自变量系数的p值均小于 0.01，说明它们对磨机成品粒径对数平均值的影响均显著。对回归结果进行异方差检验得p=0.227 5 ＞ 0.1，说明回归不受异方差的影响，不需要进行剔除异方差。以辊压力为例，分析其对成品粒径对数平均值的影响，假设磨盘转速和料层厚度恒定不变，那么辊压力的对数和平方可反映出辊压力对磨机成品粒径对数平均值的影响，如图1 所示。

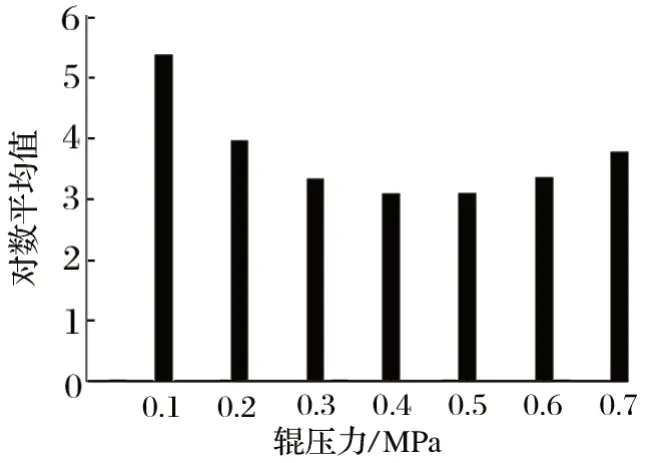
图1 辊压力对成品粒径对数平均值的影响Fig.1 Influence of roller pressure on mean value of logarithm of particle size of finished product

由图1 可以看出，辊压力对磨机成品粒径对数平均值的影响分两个阶段。第一阶段，随着辊压力的增大，磨机成品粒径对数平均值变小。可能的原因是，这个阶段辊压力较小，当辊压力增加时，颗粒之间的挤压、剪切、冲击、磨削等作用力增加，这导致更多物料被粉磨成较小的颗粒，从而使成品粒径对数平均值减小；另外，当辊压力增加时，颗粒之间的摩擦力也会随之增加，这导致颗粒之间相对运动困难，料床变得稳定，物料更容易被粉磨，从而使成品粒径对数平均值减小。第二阶段，随着辊压力继续增大，磨机成品粒径对数平均值减小到一个谷值，在此之后，随着辊压力的增大，磨机成品粒径对数平均值持续变大。可能的原因是，当辊压力超过一定阈值，要保持料层厚度不变，就需要增大喂料量，而仅仅增加辊压力对提高粉磨效率的作用已到达极限，更多未经充分粉磨的物料进入成品，由此导致成品粒径对数平均值变大，最终将趋近于喂料粒径对数的平均值。

由此可见，并不是辊压力越大，成品粒径对数平均值就越小。实际操作中，应当将辊压力调整到一个合适范围内，使成品粒径对数的平均值达到最佳。

2.2 关于成品粒径对数标准差的回归计算

用磨机成品粒径对数的标准差与磨盘转速、料层厚度、辊压力以及磨盘转速、料层厚度、辊压力的平方做回归计算，得到结果如表5 所列。

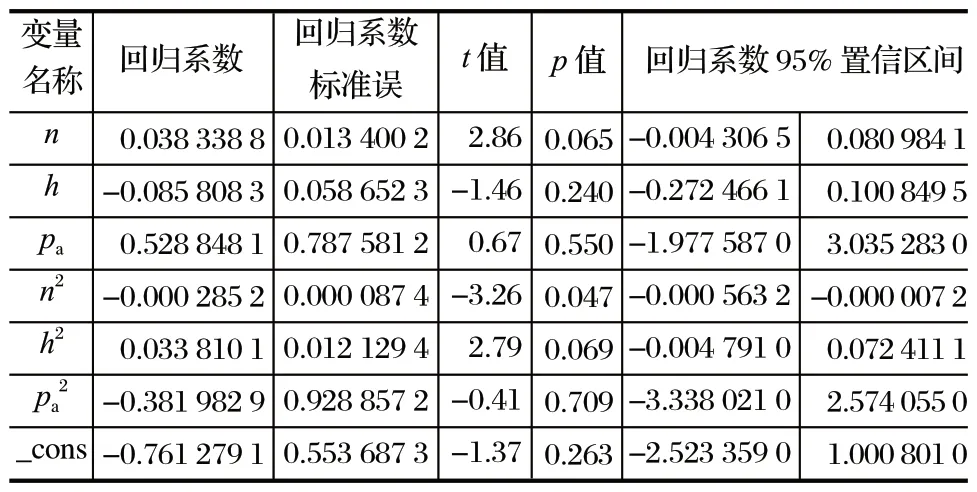
表5 回归计算结果 2Tab.5 Regression calculation result 2

由此可知，成品粒径对数的标准差、磨盘转速、料层厚度和辊压力的回归方程如下：

方程的p=0.070 6，说明回归方程在 10% 的水平上显著，只有磨盘转速显著影响磨机成品粒径对数的标准差。对回归结果进行异方差检验，p=0.986 0 ＞0.1，说明不能拒绝同方差的假设，方程不存在异方差。以磨盘转速为例，分析其对成品粒径对数的标准差的影响，假设料层厚度和辊压力恒定不变，那么磨盘转速及其平方可以反映出磨盘转速对磨机成品粒径对数标准差的影响，如图2 所示。

图2 磨盘转速对成品粒径对数标准差的影响Fig.2 Influence of grinding table speed on standard deviation of logarithm of particle size of finished product

由图2 可以看出，磨盘转速对磨机成品粒径对数标准差的影响也分两个阶段。第一阶段，随着磨盘转速的增大，磨机成品粒径对数的标准差变大。可能的原因是，随着磨盘转速的增大，更多的物料被更快地粉磨，成品中细颗粒含量增加，使成品粒径分布幅度增大，导致成品粒径对数的标准差变大。第二阶段，随着磨盘转速继续增大，磨机成品粒径对数的标准差增大到一个峰值，在此之后，随着磨盘转速的增大，磨机成品粒径对数的标准差持续变小。可能的原因是，当磨盘转速超过一定阈值，很多物料没有被充分粉磨就进入成品，同时磨盘转速的加快使料层厚度难以保持，要保持料层厚度不变，就需要增大喂料量，而仅仅增加磨盘转速对提高粉磨效率的作用已到达极限，更多未经充分粉磨的物料进入成品，由此导致成品粒径对数的标准差变小，最终将趋近于喂料粒径对数的标准差。

由此可见，磨盘转速存在一个最佳中间值，实际操作中，应将其调整到一个合适范围内，使成品粒径对数的标准差达到最佳。

需要注意的是，磨盘转速、料层厚度、辊压力等参数是协同影响立磨成品粒度分布的。另外，立磨成品粒度分布还受到原料粒度、强度、摩擦因数和密度等因素影响。因此，在实际立磨操作中，需要综合考虑这些因素，调节到最优工艺状态，并进行实际监测来验证效果。

3 结论

笔者利用 LGM/LGMS380 立磨试验台做了立磨粉磨的开路试验，根据试验结果计算出每组成品粒径对数的平均值与标准差。依据微粉碎产品粒径对数符合正态分布的理论，分别用成品粒径对数的平均值和标准差与磨盘转速、料层厚度、辊压力做了回归计算，得到其回归方程并论证其合理性，从而证明可以通过调整立磨操作参数，实现对立磨成品粒度分布特征的精准控制。

目前国内对立磨成品粒度分布与立磨参数之间关系的研究大多处于经验层面，笔者则通过试验及回归分析在二者之间构建了理论公式，指出立磨成品粒度分布与磨盘转速、料层厚度、辊压力之间的非线性关系。立磨参数存在一个最佳中间值，且所有参数是协同对成品粒度分布发生影响的，这些将有助于立磨的精准选型和操作。