翻车机振打装置的两机振动同步理论
2023-10-27张文宇陈晓哲
张文宇,陈晓哲,2,3
1秦皇岛港股份有限公司 河北秦皇岛 066000
2燕山大学 河北秦皇岛 066000
3东北大学秦皇岛分校 河北秦皇岛 066004
翻 车机是一种大型机械化散装物料卸车设备,可将敞口车厢翻转或倾斜使其完成卸料,广泛用于港口、冶金和矿山等领域。
秦皇岛港地处我国北方,在冬季时节,经过水洗后的煤炭往往冻粘在车厢内表面,出现无法卸车的冻车现象[1]。因此,需在翻车机上安装清理冻煤的振打装置,通过敲击车厢外表面产生振动,进而剥离冻煤完成卸车作业[2]。
在众多振打装置中,利用惯性原理工作的激振源最为实用,例如振动电动机,其结构简单、耐用且成本低[3],通过交流电动机带动偏心块 (简称“偏心转子”),利用偏心转子旋转产生的惯性力来驱动质体实现周期性运动。这样的设计有振动筛和振动给料机等[4]。
目前,秦皇岛港翻车机上装有单台振动电动机驱动的摆动式振打装置,在振动电动机的激振作用下,振打装置绕旋转轴往复摆动,周期性敲击车厢表面,破坏冻煤的黏结状态。在实际使用过程中,单台振动电动机产生的激振力是圆周激励,对该激振力正交分解可知,除了有迫使振打装置摆动的垂直作用分力外,还存在沿摆长方向的作用分力。因为振打装置固定在翻车机转筒结构梁上,该分力会引起翻车机出现明显的高频振动,进而引发其液压系统载荷报警[5]。因此,设计一款既保证振打装置能够摆动,又不会造成其固定端有明显振动的激振源,对于保障秦皇岛港作业具有非常重要的意义。
通过受力分析可知,若在上述振打装置结构基础上再安装一台型号相同且反向旋转的振动电动机,激振力在电动机轴心连线方向上可抵消,而在垂直于轴心连线方向上可叠加,可形成直线激振合力[6]。倘若将激振合力方向垂直于摆长方向,即可解决上述问题。但如何保证两机 (两个偏心转子) 间同步运动是需要考虑的问题。
综上,如果采用齿轮等强迫方式来实现两机同步,则会存在结构复杂,需要定期维修保养等问题,因此不是最优的设计方案[7]。考虑到振动同步理论已经成功解决了振动筛等设备上的同步问题,笔者拟采用振动同步方式来实现两机驱动单摆系统的同步运动,重点研究两机的同步及稳定性条件。
1 翻车机
目前,翻车机结构主要有两种:一种是转子式翻车机,另一种是侧倾式翻车机[8]。秦皇岛港卸煤生产线上采用的是转子式翻车机,如图1 所示。其旋转结构为 C 形转筒,由托棍支撑,在驱动装置作用下可绕轴线旋转 140°~ 170°。当车厢驶入翻车机的转筒后,液压装置首先将车厢固定,而后在转筒的带动下,车厢翻转至敞口面向下,在此过程中物料利用自重落到下方的带式输送机上,进而将煤运输到所需要的地方。
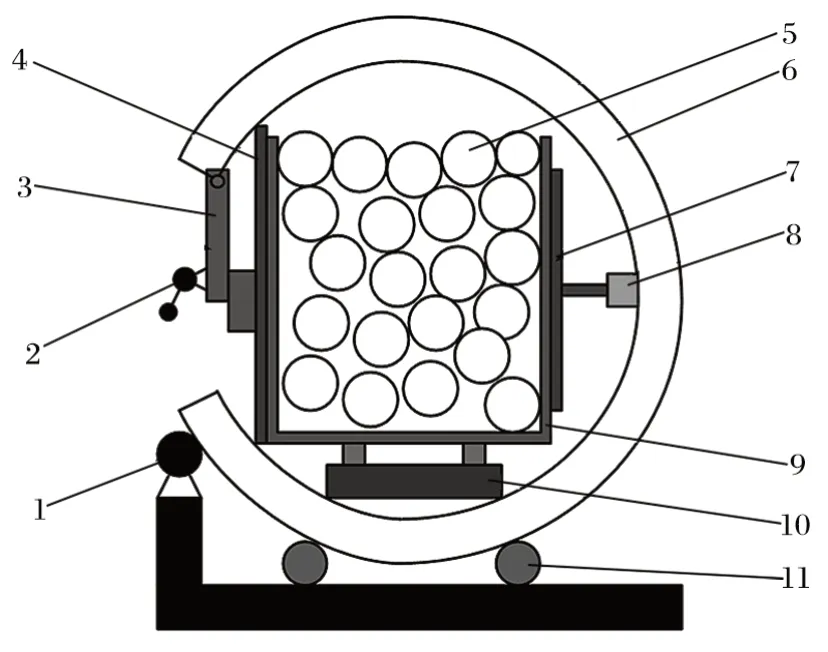
图1 转子式翻车机模型Fig.1 Rotary car dumper model
2 动力学模型
图2 所示为翻车机单摆式振打装置的两机驱动单摆系统的动力学模型 (简称振动系统),其由 1 个质量为m的单摆和其上 2 个质量分别为m1和m2的偏心转子组成。单摆安装在基座上,可绕回转中心O进行θ角度摆动。两机分别绕其回转中心O2和O3旋转运动,以φ1和φ2来表示其运动。
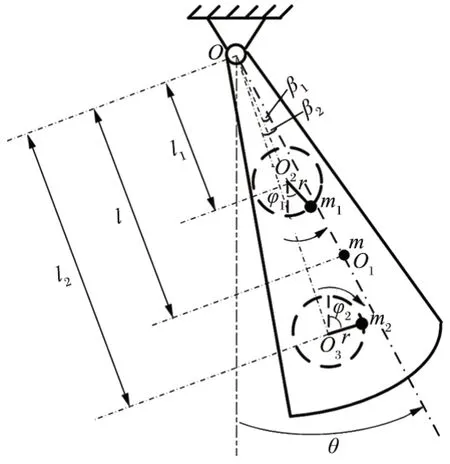
图2 动力学模型Fig.2 Dynamic model
根据拉格朗日方程,选取θ、φ1、φ2作为广义坐标,建立该振动系统的运动微分方程[9]
式中:Jθ为系统的转动惯量,kg/m3;fθ为电动机的旋转阻尼,N·m·s/rad;kθ为系统的扭转刚度,N·m /rad;r为偏心转子回转半径,m;l为单摆质心O1到O的距离,m;l1为O2到O的距离,m;l2为O3到O的距离,m;β1为OO1与OO2的夹角,(°);β2为OO1与OO3的夹角,(°);mj为偏心转子的质量,kg;fj为电动机的旋转阻尼,N·m·s/rad;Te1、Te2为电磁输出转矩,N·m。
3 解析过程
3.1 系统无量纲耦合力矩方程
设振动系统稳态运行时两机的平均相位为φ,两机间的相位差为 2α,有
由于振动系统做周期性运动,设各机角速度瞬时波动系数分别为v1、v2,得到两机的角速度和角加速度为
振动系统的稳定响应解如下
将式 (7) 中的θ对时间t求导两次,将带入式(2) 中,并在 0~ 2π 上积分,忽略v1和v2高阶项,得到单周期平均力矩方程为
式中:TL1、TL2为式 (2) 等式右端 2、3 项的积分平均值。
将式 (8) 和式 (9) 整理成状态方程形式
式中:A、B为系数矩阵;为其余项;v=[v1,v2]T。
式 (10) 即为描述两机同步运动的无量纲耦合力矩方程。
3.2 同步条件及其稳定性条件
若两机实现同步,则式 (10) 中=0。根据u=0,可得:
将式 (11) 与式 (12) 进行相减并整理,可得相位差的表达式
其中
观察式 (13),并根据三角函数特性,可得两机实现同步运动的条件为
当两机实现同步运动时,将式 (10) 在α=α0处泰勒展开,并忽略二阶以上的高阶项,引入=ωmε2和,得到同步运动的扰动方程
式中:小参数v1=ε1+ε2;v2=ε1-ε2;C为系数矩阵。
根据det[C-λI]=0,得矩阵C的特征方程为
式中:λ为特征值;c1、c2、c3为系数。
根据劳斯-赫尔维茨判据,当矩阵C的特征方程参数满足下述条件时,系统的运动是稳定的[9]。
4 数值仿真
为了验证理论分析的有效性,采用数值方式定量地讨论该振动系统的同步运动状态。数值参数来自试验机,其中m=30 kg,m1=m2=3 kg,l=0.6 m,l1=0.4 m,l2=0.8 m,r=0.15 m,β1=5°,β2=3°,ξθ=0.07,f1=f2=0.005 N·s/rad,ωnθ=38.92 rad/s。
应用上面的参数,采用龙格库塔法进行仿真,仿真时间为 30 s。采用六极交流电动机模型,设定转速为 120 r/min,振动频率为 12.56 rad/s,因此系统运行在亚共振区间。将上述参数代入式 (17) 进行稳定性判断可知,此时两机间的相位差应趋于 0°。仿真曲线如图3 所示,电动机转速稳定在 120 r/min,机体在θ方向的摆角为 -0.3°~ 0.3°,两转子相位差 2α稳定在 0°。
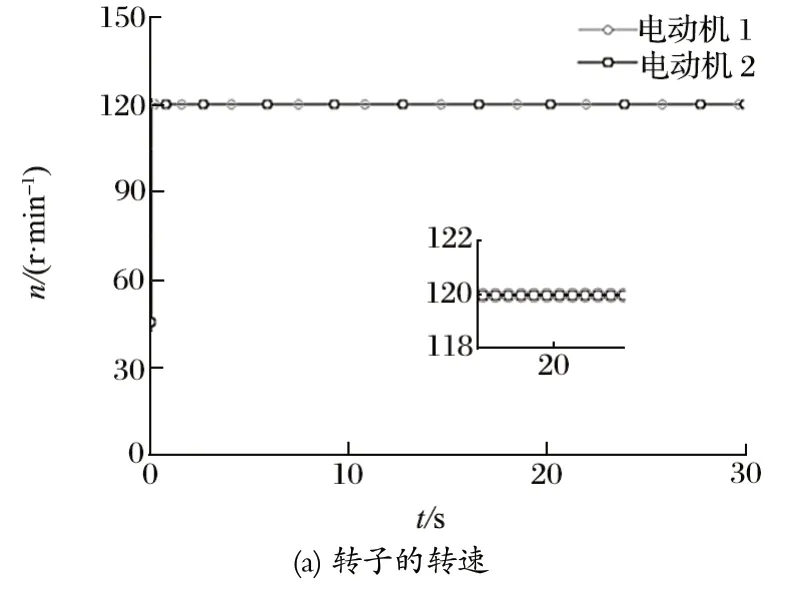

图3 亚共振的仿真结果Fig.3 Simulation results of sub-resonance
将电动机速度设定为 900 r/min,振动频率为94.24 rad/s,因此系统运行在远共振区间。将上述参数代入式 (17) 进行稳定性判断可知,此时两机间的相位差应趋于 180°。仿真曲线如图4 所示,当系统达到稳态之后,两转子相位差 2α稳定在 -180°,机体在θ方向做周期性运动,机体在θ方向的摆角为 -0.95°~0.95°,两电动机转速稳定在 900 r/min 附近。
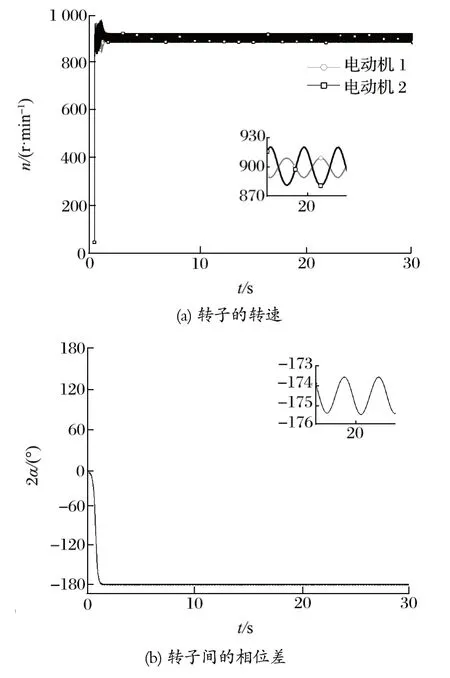
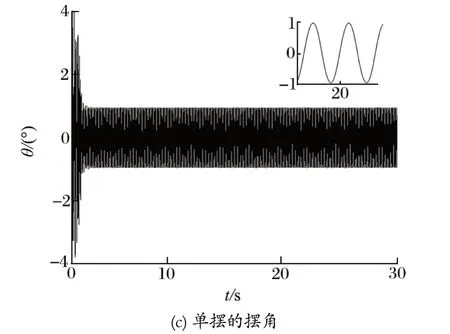
图4 远共振的仿真结果Fig.4 Simulation results of super-resonance
5 试验验证
为验证理论分析和仿真结果的正确性,采用高速摄像机对振动系统在亚共振和远共振两种状态下的运动状态进行拍摄。取偏心转子一个旋转周期内 4 个时刻的图片进行测量,如图5、6 所示。由图5、6 可知,在亚共振状态下,两机间相位差趋于 0°;在远共振状态下,两机间相位差趋于 180°。

图5 亚共振状态的高速摄像Fig.5 High speed photography of sub-resonance

图6 远共振状态的高速摄像Fig.6 High speed photography of super-resonance
通过两组试验结果,证明笔者所提理论方法的有效性和正确性。
6 结论
(1) 通过拉格朗日方程,建立了双机驱动单摆式翻车机振打装置的运动微分方程。在此基础上,应用小参数平均法研究了振动同步实现的机理,理论上获得了两机的振动同步条件及其稳定性条件。
(2) 基于稳定性判断条件,确定了系统存在两种运动状态。数值分析结果表明,在亚共振区间,两机间相位差趋于 0°,而在远共振阶段,两机间相位差趋于 180°,该结果得到了试验的验证。
(3) 证明了利用振动同步原理,可以实现所设计的振打装置中两机的同步运动。在实际工程中,应使系统的工作频率选择在亚共振状态下,这样可以保证机体获得垂直于两机轴心连线方向上的直线激振力。
