创设“辐向电场”情境 命制“进动现象”试题
——以三道物理高考试题为例
2023-10-26程红光姜付锦
程红光 姜付锦
(1.孝感高中,湖北 孝感 432100;2.黄陂一中试题研究中心,湖北 武汉 430300)
2020年1月7日出版《中国高考评价体系》,“情境“一词出现了40次,第一次在总纲中,“高考评价体系还规定了高考的考查载体——情境,以此承载考查内容,实现考查要求”; 在“四层”之“学科素养”中出现21次;在“关键能力”中出现9次;在“四翼”中出现9次,主要以“问题情境”“探究情境”等词组呈现.2021年3月13日,教育部新版发《教育部关于做好普通高校招生工作通知》指出:“在深化考试内容改革方面,2021年高考命题要坚持立德树人,加强对学生德智体美劳全面发展的考查和引导.要优化情境设计,增强试题开放性、灵活性,充分发挥高考命题的育人功能和积极导向作用,引导减少死记硬背和‘机械刷题’现象.”
1 2022年浙江省高考题

图1 径向电场示意图
A.轨道半径r小的粒子角速度一定小
B.电荷量大的粒子的动能一定大
C.粒子的速度大小与轨道半径r一定无关
D.当加垂直纸面磁场时,粒子一定做离心运动
1.1 原题解析
这个问题定性分析很方便,设粒子质量为m、电量为q、速度为v,粒子做匀速圆周运动则
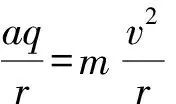
(1)
1.2 粒子与圆心最近和最远距离
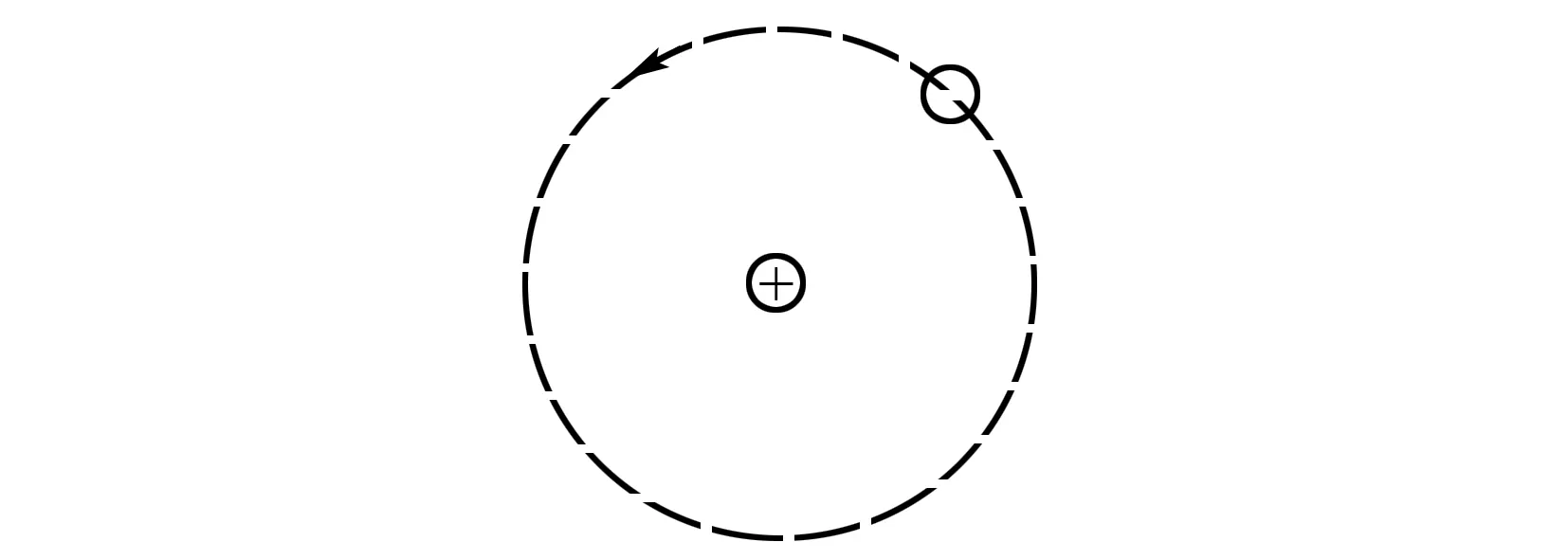
建立如图2所示极坐标系,设带电粒子质量、电量分别为m、-q,开始粒子速度为v0,到原点距离为ρ0,由带电粒子运动过程总能量守恒得

(2)
由(2)式得
(3)
若磁场垂直纸面向上,由角动量定理得
(4)
将(4)式两边同乘dt,并结合粒子初始状态值定积分得
(5)
设相关物理量数值均为1,由(3)(5)两式得
(6)
若磁场垂直纸面向下,由角动量定理得
(7)
将(4)式两边同乘dt,并结合粒子初始状态值定积分得
(8)
设相关物理量数值均为1,由(7)(8)两式得
(9)

1.3 粒子进动周期
由(5)式得,当磁场垂直纸面向上时,粒子进动周期
(10)
由(8)式得,当磁场垂直纸面向下时,粒子进动周期
(11)
1.4 粒子一个周期内进动的角度
由(5)(6)两式得,当磁场向上时一个周期内进动角
(12)
由(8)(9)两式得,当磁场向下时一个周期内进动角
(13)
(10)(11)(12)(13)四式没有解析解,有数值模拟解.

图3 磁场垂直纸面向上时 图4 磁场垂直纸面向上时粒带电粒子运动轨迹图 子到原点距离随时间变化图

图5 磁场垂直纸面向下时 图6 磁场垂直纸面向下时粒带电粒子运动轨迹图 子到原点距离随时间变化图
图3和图4是磁场垂直纸面向上时带电粒子运动轨迹图和粒子到原点距离随时间变化图;
图5和图6是磁场垂直纸面向下时带电粒子运动轨迹图和粒子到原点距离随时间变化图,可以发现它们的运动轨迹有进动现象特征[3].
2 2022年全国乙卷
一种可用于卫星上的带电粒子探测装置,由两个同轴的半圆柱形带电导体极板(半径分别为R和R+d)和探测器组成,其横截面如图7(a)所示,点O为圆心.在截面内,极板间各点的电场强度大小与其到O点的距离成反比,方向指向O点.4个带正电的同种粒子从极板间通过,到达探测器.不计重力.粒子1、2做圆周运动,圆的圆心为O、半径分别为r1,r2(R 图7 A.粒子3入射时的动能比它出射时的大 B.粒子4入射时的动能比它出射时的大 C.粒子1入射时的动能小于粒子2入射时的动能 D.粒子1入射时的动能大于粒子3入射时的动能 这个问题定性分析比较容易,通过(1)式可以发现粒子做匀速圆周运动的速度相同[4];若带电粒子受到电场力大于所需向心力时,带电粒子做近心运动,则粒子速度变大;若带电粒子受到电场力小于所需向心力时,带电粒子做离心运动[5],则粒子速度变小,故答案为BD. 建立如图2所示极坐标系,设带电粒子质量、电量分别为m,q,开始粒子速度为v0,到原点距离为ρ0,由带电粒子总能量守恒得 (14) 由(14)式得 (15) 由角动量守恒得 (16) 由(15)(16)两式得 (17) 由(16)式得粒子进动周期为 (18) 由(15)(16)两式得粒子一个周期内进动角为 (19) (18)(19)两式均没有解析解,有数值模拟解. 图8 离心运动粒子运动 图9 离心运动粒子到原点轨迹图 距离随时间变化图 图10 近心运动粒子 图11 近心运动粒子到原点 运动轨迹图 距离随时间变化图 图8和图9是粒子初速度大于匀速圆周运动速度时,粒子运动轨迹图和到原点距离随时间变化图;图10与11是粒子初速度小于匀速圆周运动速度时,粒子运动轨迹图和到原点距离随时间变化图,它们运动轨迹具有进动现象特征. 如图12所示,一带负电的质点在固定正点电荷的作用下绕核做匀速圆周运动,运动周期为T0.轨道平面位于纸面内,质点的速度方向如图12所示,现加一垂直轨道平面的匀强磁场,已知轨道半径并不由此改变,则( ). 图12 负点电荷绕固定正点电荷做匀速圆周运动 A.若磁场方向指向纸里,质点运动的周期将大于T0 B.若磁场方向指向纸里,质点运动的周期将小于T0 C.若磁场方向指向纸外,质点运动的周期将大于T0 D.若磁场方向指向纸外,质点运动的周期将小于T0 这个问题定性分析比较容易,若磁场指向纸里,则粒子受到的洛伦兹力背离圆心,粒子运动速度会变小,运动周期变长;若磁场指向纸外,则粒子受到的洛伦兹力指向圆心粒子运动速度会变小,运动周期变长,故答案为AD;若加上磁场后粒子的速度大小不变,则粒子运动规律如何? 建立如图2所示极坐标系,设带粒子质量、电量分别为m,q,正电荷电量为Q,开始粒子速度为v0,到原点距离为ρ0,由带电粒子总能量守恒得 (20) 由(20)式得 (21) 若磁场垂直纸面向上,由角动量定理得 (22) 将(22)式两边同乘dt,并结合粒子初始状态值定积分得 (23) 设相关物理量数值均为1,由(21)(23)两式得 (24) 若磁场垂直纸面向下,由角动量定理得 (25) 将(25)式两边同乘dt,并结合粒子初始状态值定积分得 (26) 设相关物理量数值均为1,由(21)(26)两式得 (27) 由(24)式得,当磁场垂直纸面向上时粒子进动周期 (28) 由(27)式得,当磁场垂直纸面向下时粒子进动周期 (29) 由(21)(24)两式得,当磁场向上时,一个周期内进动角 (30) 由(26)(27)两式得,当磁场向下时,一个周期内进动角 (31) (28)(29)(30)(31)四式没有解析解,有数值模拟解. 图13 洛伦兹力指向原点 图14 洛伦兹力指向原点时粒子时粒子运动轨迹图 到原点距离随时间变化图 图15 洛伦兹力背离原 图16 洛伦兹力背离原点时粒子点时粒子运动轨迹图 到原点距离随时间变化图 图13和图14是开始时粒子受到洛伦兹力指向原点时,粒子运动轨迹图和粒子到原点距离随时间变化图[6];图15和图16是开始时粒子受到洛伦兹力背离原点时,粒子运动轨迹图和粒子到原点距离随时间变化图[7];故若带负电粒子在加了磁场后的速率不变,则其运动轨道不再是一个圆周,会不断的近心、离心…(或离心、近心…),具有进动现象特征. 浙江卷试题只要学生能正确分析电场力与向心力关系不难做出,至于加了磁场后的情况定性分析即可;全国乙卷也只是定性分析这种辐向电场的特点,考察点基本上和浙江卷类似,但是乙卷中粒子3和粒子4的运动轨迹应该具有进动现象特征,但题中图7(b)中并没有体现出粒子运动轨迹进动现象特征,容易让人误以为是圆锥曲线;2007年全国卷试题在加磁场后粒子匀速圆周运动半径没有变化,故粒子速度会发生变化,运动周期也会发生变化,学生要做对也不难;若加磁场后粒子速率不变,则粒子运动轨迹具有进动现象特征;2022年浙江卷比全国乙卷更具开放性和灵活性,需要学生建立运动模型后才能进行全面分析.三道题通过提供辐向电场(或点电荷电场)问题情境,让带电粒子开始做匀速圆周运动,分析在加上磁场后粒子运动规律,体现“试题提供问题情境,综合考查物理建模和物理分析能力”情境化命题特点.
2.1 原题解析
2.2 粒子与原心的最近和最远距离




2.3 粒子进动周期

2.4 粒子一个周期内进动的角度
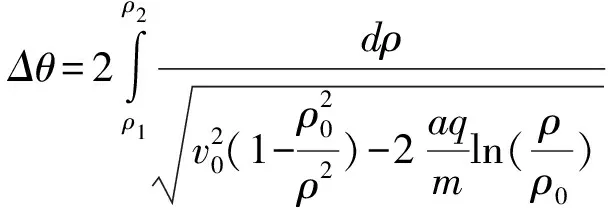


3 2007年全国卷
3.1 原题解析
3.2 粒子与原心的最近和最远距离

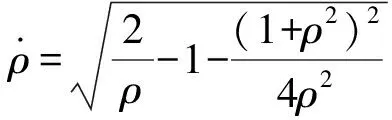



3.3 粒子进动周期
3.4 粒子一个周期内进动的角度


