综合运用函数性质解高中函数竞赛题例析

马青莲 马宇超

(扬州大学数学科学学院,江苏 扬州 225002)

马宇超,男,硕士研究生,从事数学教学研究.

函数的性质虽然较为简单直观,但是在解函数竞赛题中有着重要的作用,能够达到化繁为简,事半功倍的效果.本文通过具体的例子,对综合运用函数性质解函数竞赛题进行探究.

1 参数的值或取值范围求解

1.1 求参数的值

解析注意到f(x)在(0,10]上单调递减,在[10,+∞)上单调递增.

当a∈(0,10]时,m1=f(a),m2=f(10);

当a∈[10,+∞)时,m1=f(10),m2=f(a).

因此总有f(a)f(10)=m1m2=2 020.

解得a=1或a=100.

评注f(x)属于“对勾函数”,m1和m2随着a的变化而变化,所以需要对a的取值范围进行讨论,通过函数的单调性确定m1和m2对应的函数值,进而确定a的值.

1.2 求参数的取值范围

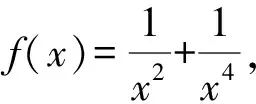
所以|a-2|>|2a+1|>0.

评注偶函数f(x)满足性质f(x)=f(|x|),f(x)在(0,+∞)单调递增,即可将求解f(a-2)|2a+1|>0.对于这类题型,可通过函数的奇偶性和单调性从而去掉“f”,解出参数的取值范围.

2 函数的值域求解

解析原函数的定义域是

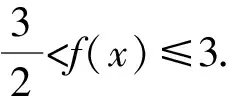
评注本题主要考查函数的单调性.首先需要求出函数f(x)的定义域,然后要在定义域内分区间讨论,判断区间上函数的单调性并求出最值,进而得到函数的值域.

3 函数最值求解

例4(2017年高中数学联赛广东预赛)设f(x)是定义在R上的奇函数,f(1)=2,当x>0时,f(x)单调递增,且对于任意的x,y∈R,都有f(x+y)=f(x)+f(y),则函数f(x)在[-3,-2]上的最大值是____.

解析因为f(x)是定义在R上的奇函数,且在(0,+∞)上单调递增,所以f(x)在(-∞,0)上也单调递增.

则当x∈[-3,-2]时,

f(-3)≤f(x)≤f(-2);

当x=1,y=1时,有f(2)=f(1)+f(1)=4.

所以f(-2)=-f(2)=-4.

所以函数f(x)在[-3,-2]上的最大值是-4.

评注奇偶性是一种对称性,奇函数在对称区间上具有相同的单调性,可判断f(x)在(-∞,0)上也是单调递增,即函数f(x)在[-3,-2]上的最大值为f(-2),再利用奇函数满足性质f(-x)=-f(x)代入解析式即可求出最大值.

4 解不等式

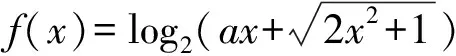
解析因为f(x)是奇函数,所以

f(x)+f(-x)=0.

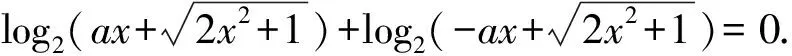
也即(2-a2)x2=0.

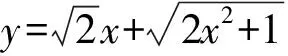
所以f(x)在(0,+∞)上单调递增.

5 证明不等式

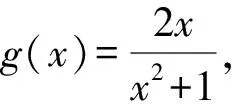
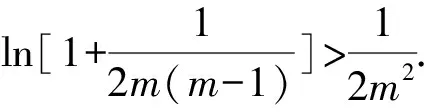
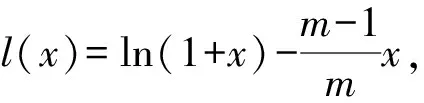
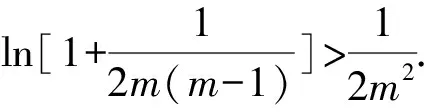
通过上面的例子可知,对于求解函数问题,往往需要综合运用函数的奇偶性、单调性、周期性和对称性等函数性质,对问题进行转化,达到化繁为简、化难为易的功效,进而解决问题.