围绕“平分” 解法溯源
——对一道含角平分线试题多视角解析
2023-10-26杜海洋
杜海洋
(四川省成都经济技术开发区实验中学校,四川 成都 610100)
题目已知圆O:x2+y2=1,定点M(3,0),过点M的直线l与圆O交于P,Q两点,P,Q两点均在x轴的上方,若OP平分∠MOQ,则直线l的方程为____.
试题内涵丰富,从知识层面看涉及直线、圆、三角形内容,主要考查利用平面图形的几何性质解直线方程;从能力层面看主要考查学生运算素养、思考探究、逻辑推理等方面的能力,突出考查数学运算、逻辑推理等素养;试题的思维过程和运算过程体现了能力立意的命题思想,较好地体现了对平面几何中的解三角形、几何图形的性质等核心内容和基本思想方法的考查,亦较好地检测考生的数学素养和学习潜能.
1 解法探究
解法1(利用面积法)设∠MOP=θ,则∠MOQ=2θ.
由S△MOQ=S△MOP+S△POQ,则有
即3sin2θ=4sinθ.




评注由已知条件构造面积相等,将其转化建立为2θ与θ的三角函数关系,然后利用单位圆的定义,求出点P的坐标,再利用两点式写出直线方程.本法的思维核心是运用了角平分线平分角这一已知条件[1].

即MP=3PQ.
又因为MB·MA=MP·MQ,

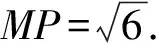
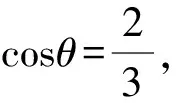
评注本法利用三角形内角平分线定理求线段MP,在△MOP中再利用余弦定理求角,从而求得点P的坐标,这一探究方法将直线与圆的割线定理及三角形的角平分线性质结合得淋漓尽致.
解法3 (利用阿波罗尼斯圆)连接PB,易得PB=PQ.


即点P到两定点M,B的比值为定值.
由阿波罗尼斯圆可得点P的轨迹方程为
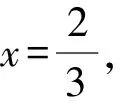
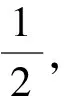
解法4(利用圆的参数方程)设P(cosθ,sinθ),Q(cos2θ,sin2θ),由Q,P,M三点共线可得
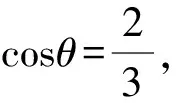
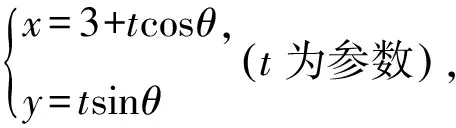
即t1t2=8,t1+t2=-6cosθ.
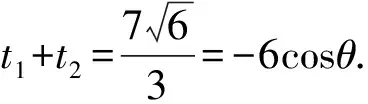
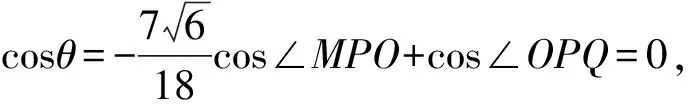
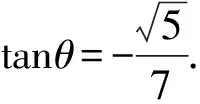

解法6 (三角形内角平分线的公式)设在△ABC中,已知三边a,b,c,如果三个角A,B和C的平分线分别是ta,tb和tc,那么,用已知边表示三条内角平分线的公式是:

=1
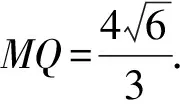
即在△OMQ中,

评注探究三角形角平分线长度与已知三角形三边长度的关系对学生的思维要求较高,基本理念是利用角平分线性质和余弦定理建立边的关系,其中cos∠MPO+cos∠OPQ=0是研究这类问题的核心步骤.

设∠MOP=θ,则∠MOQ=2θ.
利用定比分点公式
两边平方,得
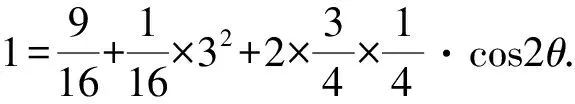
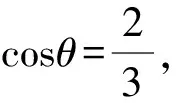
评注定比分点公式的本质为共线向量基本定理,但它体现了三个不共线向量之间的一种数量关系,利用这一关系可将三条线段的长度联系起来,这也正是结合本题已知条件运用本法的关键所在.
斯特瓦尔特定理设P为△ABC的边BC上任一点(P≠B,P≠C),则有
AB2·PC+AC2·BP
=AP2·BC+BP·PC·BC,
①

证明不失一般性,不妨设∠APC<90°,则由余弦定理,有
AC2=AP2+PC2-2AP·PC·cos∠APC,
AB2=AP2+BP2-2AP·BP·cos(∠APB)
=AP2+BP2+2AP·BP·cos∠APC.
对上述两式分别乘以BP,PC后相加整理,得①式或②式.
推论设AP为△ABC的内角平分线,则AP2=AB·AC-BP·PC.
解法8 (斯特瓦尔特(Stewart)定理)
由推论,得
OP2=OQ·OM-QP·PM.


评注解法8巧妙借用了斯特瓦尔特(Stewart)定理,不仅步骤简单,计算量也小,极大提高了解题效率,也希望同学们在平时解题中多积累相关的二级结论并加以运用.当然涉及斯特瓦尔特(Stewart)定理的试题屡见不鲜,限于篇幅,就不一一赘述,希望读者自行查找相关试题资料.
以上几种解法从不同视角进行探究,充分地体现了试题的开放性,给考生提供了较大的发挥空间. 通过以上解题过程启发我们多角度思考问题,深入挖掘问题本质,进一步寻求简便的解题方法,并及时归纳总结规律和结论,从而提高解题效率. 从以上方法可见,尤其是解法3,6,7,8这些看似高大上的结论或所谓的“技巧”并不是无源之水、无本之木,一切尽在教材(参)中!
