多视角探究2022年全国高考甲卷理数第20题

贺凤梅 李昌成

(1.新疆伊犁巩留县高级中学,新疆 伊犁 835400;2.新疆乌鲁木齐市第八中学,新疆 乌鲁木齐 830002)

题目(2022年全国高考甲卷理科数学第20题) 设抛物线C:y2=2px(p>0)的焦点为F,点D(p,0),过点F的直线交C于M,N两点,当直线MD垂直于x轴时,|MF|=3.

(1)求C的方程;

(2)设直线MD,ND与C的另一个交点分别为A,B,记直线MN,AB的倾斜角分别为α,β,当α-β取得最大值时,求直线AB的方程.

1 总体分析

本题是2022年全国甲卷理科数学第20题,是本卷压轴题之一,第(2)问是蝴蝶定理背景下的直线与抛物线的综合题. 试题命题立意新颖,低起点、入口宽,适合多视角探究解答. 试题能充分考查学生的运算能力、转化与化归的能力,属于难题. 笔者针对此题,拟从不同的角度进行分析解答,不断优化解题思路,揭示问题的本质,先分享于此,以飨读者.

2 试题解答

2.1 第(1)问解析

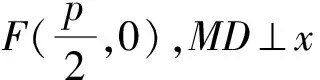
解得p=2,所以C:y2=4x.

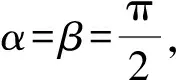
2.2 第(2)问解析

y2-4my-4=0.

由根与系数的关系,得

y1+y2=4m,y1y2=-4.

①

设MD:x=ny+2,A(x3,y3),B(x4,y4),

y2-4ny-8=0.

由根与系数的关系,得

y1+y3=4n,y1y3=-8.

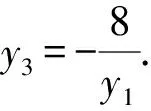
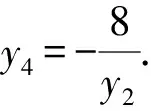
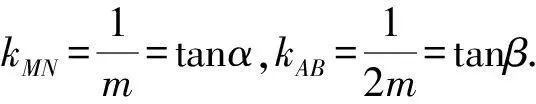
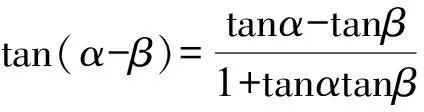
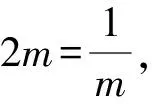
而当m<0时,α-β无法取得最大值.

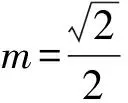
所以直线AB方程为

评注此问的显著特点是有很多的点和线,但仔细观察发现这些点和线相互关联,只需定好其中一个点,就可以很好地联系其他的点和线,容易寻求相同的结构,利用同一法求解,简化运算,解法1很好地诠释了这一思路和解答过程.

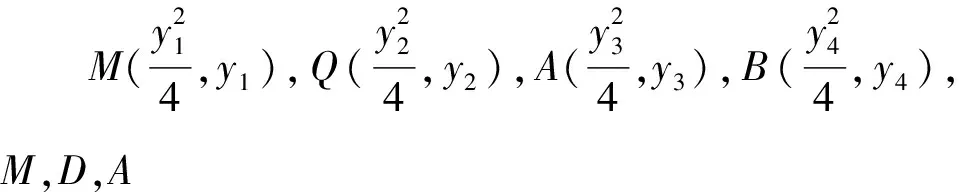
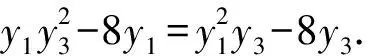
即(y1-y3)(y1y3+8)=0.

显然y1≠y3.

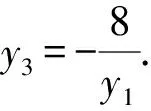
因为N,D,B三点共线,则kND=kBD.

同理可求得y2y4=-8,

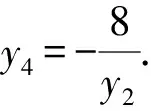
设直线MN的方程为x=my+1(m≠0),

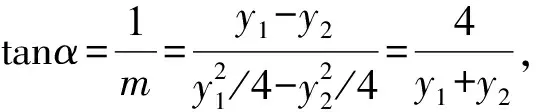
由解法1中①式可知

y1+y2=4m,y1y2=-4.

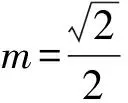
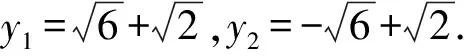
故直线AB方程为

评注此解法的特点在于根据三点共线,斜率存在时,利用斜率相等找到点的纵坐标之间的内在联系,进而找到两直线MN与AB斜率之间的关系,借助于基本不等式,求出当α-β最大时kAB的值,利用取等条件得出m的值.进而求出y1,导出y3,再求出x3,即得点A的坐标,最后求出直线AB的方程.只要理清解题思路,加上适当的计算能力及技巧,解题可以顺利进行.

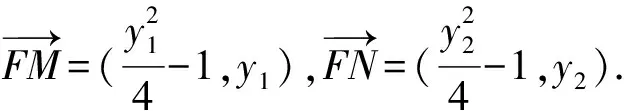
化简整理,得

(y1-y2)(y1y2+4)=0,且y1≠y2.

所以y1y2=-4.

②

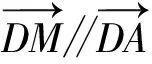
即(y1-y3)(y1y3+8)=0.

因为y1≠y3,故y1y3=-8.

③

同理y2y4=-8.

④

由②③,得y3=2y2,

由②④,得y4=2y1,

所以kMN=2kAB,tanα=2tanβ.

要使α-β最大,必有α>β,且α,β均为锐角,

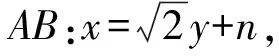
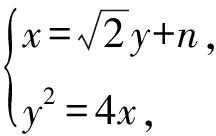
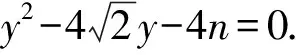
所以y3y4=-4n.

而y3y4=4y1y2=4×(-4)=-16,

所以n=4.

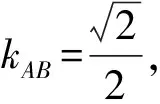
所以2n·(m2-1)-2m·(n2-1)=0.

化简整理,得

(m-n)(mn+1)=0,且m≠n.

所以mn=-1.

同理由D,M,A和D,N,B三点分别共线求得am=-2,bn=-2.

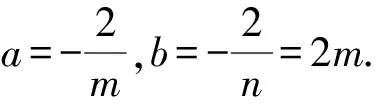
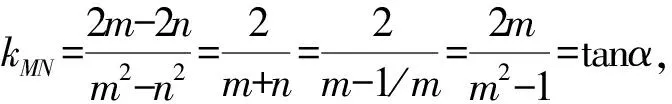
所以kMN=2kAB,tanα=2tanβ.

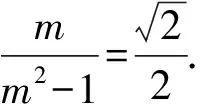
评注此解法用到了抛物线的参数方程,求解更简洁,教材对于抛物线的参数方程仅在课本选修4-4中简单提及,学生不一定熟练掌握,需要老师们留心.

3 总结升华

通过研究高考真题,发现在复习备考的征途中,特别是对于一些有文化背景的题,教师要有足够的耐心,深度解析各种方法,让学生在比较中开拓思路.因此,我们要充分利用好高考经典试题,从不同视角、不同解法深度解读,长此以往,一定能提升复习备考的效果[2].