船用汽轮机转速线性自抗扰控制研究
2023-10-25张荣彬郭永飞
张荣彬,郭永飞
(中广核研究院,广东 深圳 518000)
0 引言
随着国家海洋强国战略的推进,船用核动力装置的研究发展迅速。汽轮机作为船用核动力装置的核心设备,其控制性能的好坏直接影响船舶的机动性和安全性,尤其近年来孤网技术的发展,对船用核动力装置及其参与孤网发电的汽轮机调节提出了更高的要求。由于孤网的抗扰动能力差且负荷波动范围大,对机组一次调频的灵敏度、调节幅度及响应速度要求高[1],且船用汽轮机调速系统中常包含死区、惯性等非线性环节,采用传统的线性PID 控制较难保持良好的控制性能。
目前,国内外众多学者对汽轮机转速控制系统的设计展开了广泛研究。王元慧[2]等针对船用核动力装置设计了串级前馈-反馈模糊PID 控制,实现汽轮机转速的稳定控制;李明辉[3]等采用模糊控制和内模控制相结合的方法,通过粒子群算法对控制器参数自适应调整,有效提高了汽轮机调速系统的响应速度和抗扰性能;杨旭红[4]等针对核电站汽轮机转速控制系统中的不确定性和非线性,运用改进的PSO 算法对PID 控制器参数进行优化设计,该方法增强了系统稳定性,具有响应速度快,超调小等优点,明显改善了汽轮机转速的控制品质;詹锦皓[5]等提出基于串级前馈PID 协调控制的汽轮转速控制系统,采取负荷变化量作为前馈控制,在故障情况仍可维持汽轮机转速稳定,具有较好的容错性。可见,设计结构简单、抗干扰能力强、鲁棒性好,且不依赖于系统精确模型的控制器,提高了汽轮机转速控制性能,对于船用核动力装置工程的实践应用有着重要意义。
自抗扰控制(active disturbance rejection control,ADRC),其核心是将被控对象自身的不确定性与外部干扰一并视作“总扰动”[6],利用扩张状态观测器(extended state observer,ESO)进行实时估计并补偿自抗扰控制作为一种先进控制算法,不仅具备PID 控制结构简单的优点,且不依赖精确的系统模型,但由于其参数过多导致整定困难,实践中未能广泛应用。为此,Gao[7]提出将非线性ADRC简化为线性形式(linear active disturbance rejection control,LADRC),使控制器参数得以简化,同时又继承了ADRC的优点。研究表明[8],通过设计合适的LADRC 结构,调整线性扩张状态观测器(LESO)的带宽,可有效提高系统控制性能。
本文提出一种基于线性自抗扰控制的汽轮机转速控制策略,以优化数字电液系统控制性能。通过建立船用汽轮机的数学模型,采用MWorks 软件的Sysplorer 仿真环境,搭建基于LADRC 的汽轮机调速系统模型。仿真结果表明,此方法具有稳态误差小、响应速度快、超调小等优点,明显改善了汽轮机转速的控制品质。
1 船用汽轮机调速系统建模
根据汽轮机调速系统的工作原理,船用汽轮机转速控制系统一般可简化为由调速器、控制器、电液转换器、油动机、蒸汽容积、转子6 部分构成的数学模型。
1.1 调速器数学模型
由于制造工艺的不断完善,调速器质量和摩擦阻尼可忽略不计。本文采用理想的调速器模型,即:
式(1)中:δ为汽轮机转速不等率;ζ为调速器滑环位移变化相对值;φ为转速变化的相对值。其传递函数可表示为比例环节:
1.2 电液转换器数学模型
电液转换器是将电信号控制指令转换、放大为液压信号,由油动机去控制调节阀,实现自动调节。电液转换器模型可表示为电液转换器滑阀位移Xv对力矩马达电压U 的传递函数
式(3)中:Ka为伺服放大器增益;Kxv为伺服阀增益;Kvf为力反馈回路的开环放大系数;ωmf为力矩马达固有频率;ζmf为力矩马达的阻尼比。当力矩马达的固有频率ωmf足够大时,在仿真过程中对各物理变量进行无量纲化处理,则电液转换器的传递函数可以简化为
式(4)中,Te为电液转换器时间常数。
1.3 油动机数学模型
油动机为汽轮机调节系统中驱动调节汽阀的执行机构,本文所采用的油动机类型为单侧进油阀油动机。当滑阀移动时,油动机的进油流量为
式(5)中,μ为油口的流量系数;Xv为滑阀的位移变化量;b为油口的宽度;ρ为压力油密度;p0为进油压力;p1为进入活塞底部后油的压力。油动机排油流量与进油流量相等,忽略油运动的惯性力,并将进油量等效为单位时间内活塞移动扫过的体积,可得活塞行程的变化率为
式(6)中:pd为出口油压力;A 为进油侧活塞有效面积。进而,油动机的传递函数可以简化为
式(7)中:Tc为油动机的时间常数。
1.4 蒸汽容积数学模型
假设蒸汽流经体积为V的容器,根据气体流动的连续方程,可以得到进、出口流量的变化量与容积内质量的关系表达式为
式(8)中:q1和q2分别为进口和出口流量,kg/s;ρ1为蒸汽密度,kg/m3。对式(8)进行泰勒展开并略去其高阶项,考虑到蒸汽容积的气体喷口面积不变,可得到稳定状态下气体体积变化量Xs1,进而推导得到蒸汽容积传递函数为
式(9)中:Xp为压力相对变化量;Tρ为进汽容积时间常数。
1.5 转子数学模型
影响汽轮机转子运动的因素有汽轮机的蒸汽转矩MT,负载的反转矩ML,摩擦转矩Mf。由于Mf远远小于MT和ML,可以将其忽略,因此转子的力平衡方程为
式(10)中,J为转子的转动惯量;ω为转子角速度。再由蒸汽压力与转子角速度关系和角速度与时间的关系,同时忽略转子的自平衡能力,可得转子传递函数表达式为
式(11)中,Td为转子时间常数。
2 线性自抗扰控制器设计
LADRC 主要由线性状态观测器(LESO)和线性状态误差反馈控制律(LSEF)两个部分组成。典型二阶系统的LADRC 控制器基本结构如图1 所示。
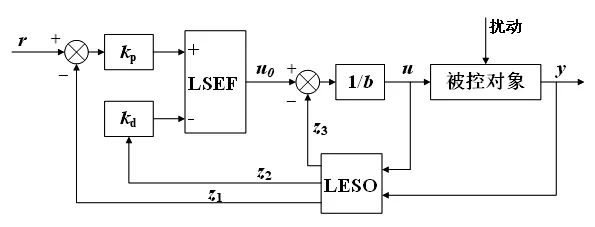
图1 LADRC基本结构Fig.1 Basic structure of LADRC
图1 中,r-设定值信号;u0-LSEF 计算输出信号;u-控制输出;z1-输出信号(y)的观测值;z2-y 的一阶微分的观测值;z3-总扰动的观测值。
2.1 线性扩张状态观测器
一般地,考虑二阶系统:
式(12)中:u为系统输入;y为系统输出;b为控制增益;w为系统不可测扰动;f为系统内外部扰动的总和。令x1=y,x2=,x3=f,假设f可微,定义3=h,将式(12)用状态空间表示为
式(13)中,x为系统状态变量,y是输出。式(13)可写成以下方程组形式:
建立线性扩张状态观测器(LESO)[7]:
式(15)中,z为x的观测值;为LESO 的输出;L为观测器增益向量,可通过极点配置等方法来获得:
式(16)中:ω0为LESO 的带宽,选取合适的观测器带宽,LESO 就能够实现对式(14)中各变量的实时跟踪。
2.2 扰动补偿
控制器控制量设计为
将式(17)代入式(12)中,并忽略z3对f(y,,w)的误差,即式(12)可简化为一个双积分串联结构:
这样通过LESO 即可对系统总扰动进行观测,并在其对系统产生影响之前进行补偿。
2.3 线性状态误差反馈控制
在对扰动进行补偿之后,再对被控对象施加控制律:
式(19)中:r为给定信号;kp、kd为控制器增益,根据式(18)~式(19)可得系统闭环传递函数为
式(20)中的特征多项式表示为:
式中,kp=ωc2,kd=2ζωc,定义ωc为控制器的带宽,则ωc为控制器中唯一需要整定的参数。
2.4 控制器参数整定
根据前文分析,LADRC 主要参数为观测器带宽ω0、控制器带宽ωc、补偿系数b0。控制器参数一般是根据对研究对象的了解,凭经验进行调节,但在实际整定过程中遵循以下规律[9]:
1)ω0越大,LESO 的响应越快,但这会使观测器对噪声更加敏感。因此,首先赋予ω0一个较小的值,然后逐渐增大至观测精度满足要求为止。
2)ωc越大,系统输出响应越快,控制作用越强。当ω0与ωc的比值越大,系统的相角裕度越大,系统越稳定。增加ω0值或者ωc值都会引起高频带增益变大,系统的抗噪声能力下降。
3)当系统迟延较大时,一般选取较小的b0值。在观测向量z3产生变化时,可使扰动补偿(u0-z3)/b0变化更加灵敏,从而快速调节系统的输出量。
应在保证控制系统稳定的前提下,进行多次试验和误差指标对比,最终确定合适的控制器参数。
3 仿真分析
为验证本文所提出的基于LADRC 的船用汽轮机转速控制的有效性,在MWorks/Sysplorer 仿真平台建立汽轮机调速系统模型和LADRC 控制器,开展汽轮机转速LADRC控制系统仿真验证,并与经典PID 控制方法进行对比。汽轮机转速LADRC 控制系统结构如图2 所示。
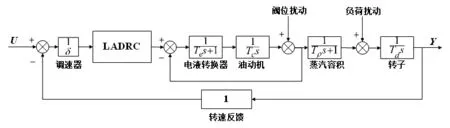
图2 汽轮机转速LADRC控制系统框图Fig.2 Block diagram of LADRC control system for turbine speed
采用文献[10]方法对某船用核动力装置汽轮机调速系统参数进行辨识,得到模型参数见表1。

表1 汽轮机调速系统模型参数Table 1 Model parameters of steam turbine speed regulation system
3.1 汽轮机转速指令跟踪性能对比
为检验本文所设计的汽轮机转速控制系统输出跟踪转速指令信号的性能,在没有外部扰动的情况下,分别在传统PID 和LADRC 转速控制系统输入端加入阶跃信号,采用固定步长0.01s 进行仿真,考察系统输出跟踪转速指令信号的快速性和准确性。PID 参数设置为kp=10、ki=1、kd=1;LADRC 控制器参数设置为ω0=5、ωc=20、b0=0.4。两种控制系统转速指令阶跃变化时的输出响应仿真结果如图3 所示,控制器的性能评估结果见表2。从图3 和表2 可以看出,传统PID 控制调节时间长,超调量大,上升时间慢;而采用LADRC 控制器时,控制系统的输出能够快速、准确地跟踪输入指令,并且快速稳定到设定值,其上升时间减少了1.74s,超调量则减少了7.2%,且提前17.55s 到达稳定。

表2 控制器性能评估结果Table 2 Performance evaluation results of controller
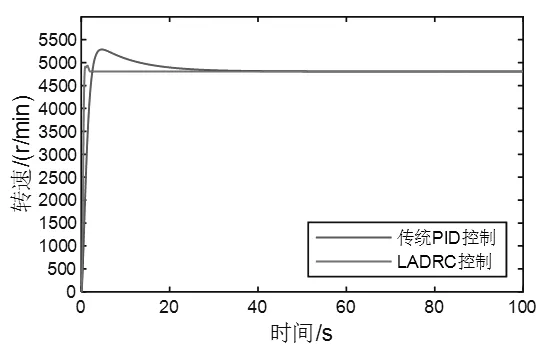
图3 汽轮机转速指令阶跃特性曲线Fig.3 Step characteristic curve of turbine speed command
3.2 汽轮机抗扰性能对比
为验证所设计的控制器的抗扰效果,在60s 时加入20%的阀位阶跃扰动,系统响应如图4 所示。在60s 时加入甩100%负荷的阶跃扰动,系统响应如图5 所示。从图4和图5 可见,在引入阀位扰动和甩负荷扰动情况下,采用LADRC 控制方案转速飞升幅度更小,且更快恢复稳定,说明LESO 对扰动的补偿估计能够更好地抑制扰动,提升控制系统的抗扰性能。
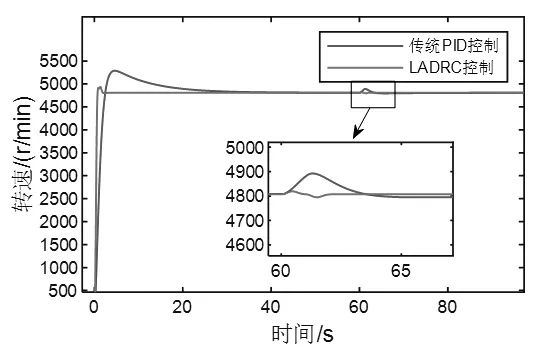
图4 汽轮机阀位扰动下仿真结果Fig.4 Simulation results of steam turbine valve position disturbance
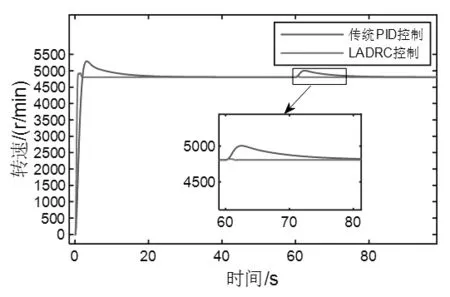
图5 汽轮机甩负荷时仿真结果Fig.5 Simulation results of turbine load rejection
4 结语
本文研究了孤网模式下船用汽轮机转速的线性自抗扰控制策略,通过理论推导和系统辨识建立了汽轮机转速控制系统的数学模型。分别对PID 控制和LADRC 控制系统进行了设定值跟踪性能和抗扰性能对比实验,仿真结果表明:
1)相比传统PID 控制,采用LADRC 的船用汽轮机转速控制超调量更小、调节时间更短,具有较好的动态响应特性和稳态特性。
2)LADRC 控制器有较好的抗干扰性能,线性扩张状态观测器的引入使得LADRC 对外界的干扰起到较好地抑制作用。
