地震作用下的抗滑桩支护边坡模拟分析

闫博华

(山西省交通规划勘察设计院有限公司 太原市 030032)

0 引言

我国是一个多山国家,同时也是一个地震带居多的国家,在当前交通系统大力发展的背景下,工程边坡治理工程越来越多。地震是带来滑坡灾害的重要原因之一,因此对边坡工程在地震荷载下的稳定性研究显得尤为必要。

国内外学者对边坡地震方面的研究已有很多成果,于玉贞等[1]进行了抗滑桩静力和动力下的离心模型试验,对两种混凝土抗滑桩开裂的情况的破坏和受力情况进行了分析,得到静力开裂在地震后桩底转为活动铰约束,其弯矩呈先增大后减小的趋势。同时在饱和砂土的抗滑桩加固的动力离心模型试验[2]中对饱和砂土的地震动力响应进行了研究,明确了地震作用对地基液化的附加弯矩值应引起重视,为边坡的抗震设计提供了重要参考依据。吴永等[3]以极限定理为理论基础,在确认边坡滑动面的前提下,从能量角度对抗滑桩加固体系进行了计算,得到了坡体与锚固体系临界的计算模型,对抗滑桩的失效机理进行了深入探索。许江波等[4]对动力作用下抗滑桩支护的边坡提出了新的抗震设计方法,得到了桩体在边坡受地震作用下的内力值及分布规律,并用具体的边坡模型验证了新方法的可行性,为边坡稳定性的计算提供了新的思路。孔纪名等[5]对地震荷载作用下抗滑桩桩身埋入深度进行了研究,以工程实例为依托,采用相似性原理进行了物理模型试验,最终得到了抗滑桩最佳的嵌固深度,以此为基础建立了抗滑桩最佳嵌固深度的判据。唐勇等[6]采用FLAC 3D数值模拟的方法对断层破裂带边坡的抗滑桩加固机理及模式进行了研究,在地震荷载下断层带向临空面滑动,抗滑桩在加固边坡的过程中土拱、桩身等都起到了良好的加固作用,最终得到了抗滑桩边坡最合理的参数设计。

自汶川地震后,我国工程建设对结构在地震荷载作用下的抗震要求越发严格,《公路工程抗震规范》(JTG B02—2013)中明确了边坡在抗震设计中的方法及要求,但传统的静力法与实际工程相差较大。文章依托某高速边坡治理工程,对锚索抗滑桩加固边坡的抗震性能进行研究,以期为工程实际提供参考。

1 存在的问题

目前边坡的稳定性常用静力法,静力的强度折减法主要是将土体的强度参数进行折减,达到滑坡的极限平衡状态时,强度折减系数则作为边坡的稳定系数。但在边坡地震作用下,边坡的破坏是一个累积的过程,并不是静力法所在一个瞬时的状态,因此判定边坡在动力响应时的破坏判据是一个关键性问题,目前主要有3种方法对动力作用下边坡的稳定性失效作为判据,一是形成贯通裂缝;二是在地震过程中边坡某部分位移出现突然增大;三是在模型计算中不收敛。这三个方法虽在一定程度上可作为判据,但边坡的动力特性是一个复杂的问题,还应通过多方面计算复核。

2 工程概况

高边坡的治理通常是边坡工程中的重难点,依托工程为某高速K5+153.321～K5+251.265段,该段拟建公路两侧均为山区路段,高差起伏较大,路线呈南北走向,高速公路的设计时速为120km/h,现场勘查显示,路线周边环境较好,无河流水域,植被发育完好,自然边坡较为陡峭,在拟建工段边坡有少数裂隙,未发现明显滑移痕迹。其中在桩号K5+170断面的坡高最高,约27m,岩层断面显示为顺层,对边坡的稳定极为不利,需对该断面进行重点分析。如图 1所示。

图1 K5+170横断面(单位:m)

地勘资料显示,该工段的地层条件复杂,在K5+170断面的地层主要为4层,分别为填土(厚约4.6m)、粉质黏土(厚约8m)、全风化玄武岩(厚约9.6m)、强风化玄武岩(厚约12m)。规范中采用静力法规定,高速公路路堑边坡在坡高大于20m时,边坡的抗震稳定系数不应小于1.15。因此,在边坡的加固设计中应加强对边坡抗震稳定性的设计。拟定边坡加固方案采用预应力锚索抗滑桩的形式,抗滑桩距离坡脚8m,桩身长23m,采用矩形截面,截面尺寸为1.2m×1.5m,自桩顶向上进行坡面放坡处理,坡率均为1:1.5,每级边坡均为6m,一、二级边坡之间设置2m宽的平台,坡面采用骨架草籽护坡。锚索锚固与全风化玄武岩中,采用压力分散型锚索,其预应力为150kN。如图 1所示。

3 数值模拟研究

3.1 模型的建立

采用有限元软件对依托工程建立有限元模型,模型尺寸100m×60m。各个土层的模拟采用摩尔-库伦本构模型,锚索和抗滑桩采用弹性本构模型,抗滑桩截面尺寸为1.2m×1.5m,长度为23m,采用1D梁单元进行模拟,锚索划分为固定段和自由段两种网格,在自由段施加预应力。网格划分以控制模型计算精度和效率为原则,在精度要求高的区域网格密度为1m。其余部分的网格密度均为2m。土层、抗滑桩、锚索的模型材料参数根据地勘等资料进行选取,计算模型如图 2所示,模型的具体参数如表 1所示。

表1 模型参数表

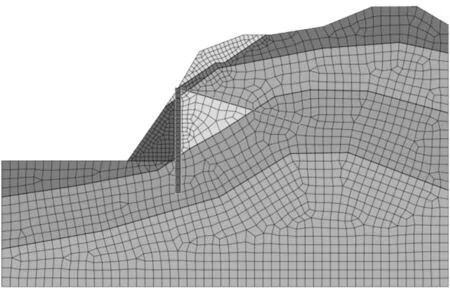
图2 有限元模型

3.2 地震荷载

模型建立后对边坡的稳定性和变形进行分析,地震荷载的施加选择EL-Centro波,峰值加速度为0.214g,持续时长为53.46s,地震时程如图 3所示。在动荷载分析时,选择非线性时程+SRM,具体模拟步骤如下:

(1)原始边坡模拟,位移归零;

(2)对边坡进行1∶1.5削坡处理;

(3)施加锚索抗滑桩加固措施;

(4)挖除桩前土体;

(5)施加地震荷载;

(6)计算结果数据提取。

图3 EL-Centro地震波时程图

3.3 计算结果分析

提取有限元计算结果的塑性区分布云图如图4所示。

图4 边坡有效塑性区云图

塑性区云图反映了土体的破坏程度。在塑性变化大的区域,土体破坏的可能性越大。从图中可以看出,坡体在坡脚处的塑性破坏区最严重,并向坡顶延伸,说明边坡的潜在滑动面就在这个塑性区内,主要位于岩层分界线上。

对边坡在各个模拟阶段的稳定系数进行分析,可有效指导施工时各阶段边坡的稳定情况,如图 5所示。

图 5 各模拟阶段边坡稳定系数

在模拟自然边坡时,边坡的稳定系数为1.05,边坡的稳定系数较小,稳定性未达到规范要求,然后进行放坡1:1.5后削坡状态的模拟,此时边坡的稳定系数为1.15,同比增长9.5%,边坡的稳定性增长有限,边坡的稳定性还有待提高。在施加支护结构预应力锚索抗滑桩后,边坡的稳定系数提升到1.81,增幅较大,最后开挖桩前土体,边坡的稳定系数降低到1.65。这种现象说明,在边坡稳定性的提高方面,削坡措施只降低了部分土体的下滑力,并没有明显改善整个坡体的整个受力状态,因此对边坡的稳定系系数提高并不明显。抗滑桩支护结构改了坡体的受力状态,限制了潜在滑动土体的位移趋势,改善了整个滑体的受力体系,从而极大地提高了边坡的整体稳定性系数。而桩前土的开挖,将桩前部的被动土压力去除,使得抗滑桩的悬臂段长度增加、嵌固段减小,侧向土压力增大,导致边坡的稳定性下降,因此在有条件的情况下应尽量减小桩前土的开挖,保留桩前土有利于边坡的稳定。

对地震荷载作用下边坡稳定系数的变化进行分析,对地震荷载取其前4s进行数据提取。在前4s内,地震已经经过峰值加速度的变化,边坡已经经历了地震荷载的峰值变化,每0.5s进行数据提取,得到图 6所示的边坡安全稳定系数变化图。

图 6 地震荷载下边坡安全稳定系数

从图 6中可以看出,边坡在整个地震荷载作用下的稳定系数变化呈下降趋势,结合边坡地震荷载的时程图分析,边坡在前0.5s的稳定系数下降较少,在1.5～2s之间下降速率增加,在2.5s后区域稳定在1.16左右。对照地震波时程图来看,在1s以前,地震波的峰值有小幅度变化,并未达到峰值,在1.5～2s时,地震波达到峰值加速度,在4s左右峰值加速度最小,因此得到的边坡稳定系数下降也呈现出类似阶梯状的变化情况。这也说明,预应力锚索抗滑桩在边坡的抗震过程中起到了良好的效果,边坡的稳定系数未在短时间内呈断崖式下降。这是因为预应力锚索抗滑桩既有抗滑桩的刚性,也有锚索的柔性作用,在地震荷载传递到土体时,抗滑桩与土层相互挤嵌,锚索提供了相对的弹性变形,形成类似缓冲的效应,能在一定程度内吸收地震荷载的能量,保证边坡的稳定。

如图7所示为桩身地震前后的位移变化图。

图7 桩身水平位移变化图

从图 7可以看出,在震前桩身上部的水平位移向临空面移动,下部水平位移向坡背移动,整个桩身的水平位移呈弧形变化,这说明预应力锚索在限制桩身的位移上有较好的作用。地震荷载后,桩身整体向着临空面进行可移动,桩顶水平位移最大为17cm,桩底为5.8cm,桩顶的水平位移变化幅度大于桩底,这是由于地震作用的效应,上部结构主要为悬臂式受力体系,受地震作用时桩体受到的阻尼较小,因此其位移变化较为明显。而桩体下部嵌固于土体中,在水平地震力作用下,桩体受到土体的阻滞作用,因此其位移相对较小。

进一步提取抗滑桩的弯矩如图8所示。

图8 桩身弯矩图

从图 8可知,抗滑桩在两种工况下弯矩的最大值均位于桩身中部,两端较小,地震荷载的作用下,抗滑桩桩身弯矩的形态未变,大小发生改变,地震荷载的最大桩身弯矩值为3480kN·m,在设计中应加强对抗滑桩中部的结构设计。

4 结论

文章采用有限元软件模拟分析了锚索抗滑桩静力和动力荷载下的位移及稳定性变化规律,得到如下结论:

(1)边坡在静力作用下的潜在滑动面位于岩层分界面,稳定系数在各个工况呈先增大后减小的变化情况。

(2)地震荷载作用下边坡稳定系数的降低呈阶梯状下降,最后稳定于1.16。

(3)地震荷载前,边坡的水平位移值桩顶向边坡临空面移动,桩底向坡背移动;地震荷载后,桩顶和桩底的水平位移均向临空面移动,最大值为17cm。

(4)桩身的弯矩值在地震前后的变化形态一致,呈中间大两端小的变化形态,地震后桩身的弯矩值大于地震前。