一种基于电流信号积分的新型功率振荡闭锁和解闭锁方法研究
2023-10-25孙超李梅
孙 超 李 梅
(安徽理工大学电气与信息工程学院,安徽 淮南 232001)
0 引言
近些年,因为继电器误动作导致大规模停电的事件频频发生。北美的一项研究报告显示,在近些年发生的停电事故中,有近80%的事故源于继电器的误动作,尤其是2003年的美加大停电、2012年发生在印度的大规模停电,这些事件引发了作者对此类问题的思考[1-3]。一次大停电,即使是数秒钟,也不亚于一场大地震带来的破坏。作为电力系统常用的保护设备,距离继电器在很久之前就已经具备了功率振荡闭锁(PSB)功能和功率振荡解闭锁(PSD)功能,尽管如此,但由于故障的复杂性,该功能一直在改进中。为了能够应对各种复杂情况,距离保护的PSB和PSD功能应该满足以下基本要求:1)系统发生对称和不对称功率振荡(PS)时,距离继电器应能实现快速闭锁。2)在对称和不对称PS期间发生不对称故障,保护装置应能实现有选择的动作跳闸。3)在对称和不对称PS期间发生三相故障,保护装置应能可靠动作跳闸。
为此,国内外学者进行了大量研究。文献[4-6]采样振荡中心电压识别故障,该方法只针对对称故障;文献[7]利用线路两端电压夹角识别故障,但其通道的可靠性需要保证,并且两端电气量增加了数据处理过程;文献[8-9]使用Lissajous图识别振荡期间的故障,该方法同样需要两端电气量,复杂的计算过程限制了方法的实际应用;文献[10-11]使用振荡期间测量阻抗变化率实现故障检测,当系统处于不稳定振荡时,阻抗变化同样很快,这可能妨碍基于阻抗变化率的方法在不稳定情况下的正确决策。
1 提议的新方法
作为电力系统的重要保护装置,距离继电器需要识别电力系统的PS和故障状态,已有文献研究的方法如FFT、WTS等,数据采样率高,算法复杂,然而电力系统保护对保护动作时间有一定要求;简单的算法虽然响应快,但是存储信息也较少。鉴于此,本文提出了对电流信号在时间轴上进行积分的新方法,图1为一段系统电流信号波形图,由图可知,发生故障前后,电流波形在时间轴上的积分发生变化,因此,利用积分的差异来实现PSB和PSD功能是可行的方案。
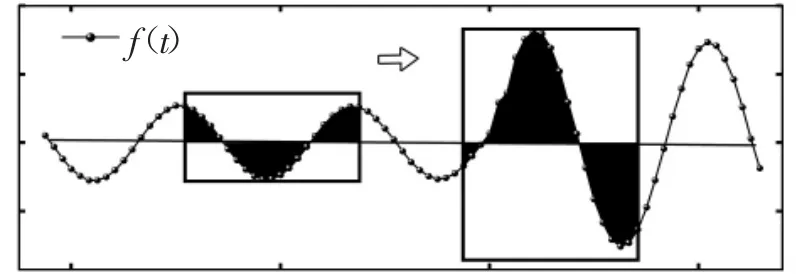
图1 移动窗口
1.1 求积公式的选择
电力系统中电压、电流可以用时域中的数学表达式进行如下表示:
式中:A为信号的幅值;f1为信号的基频;φ为相位角。
利用大名鼎鼎的Newton-Leibniz公式(2)就可以对其进行积分,但是,在实际情况下,这并非可行的操作,实际情况可能面临着频率偏移、谐波和负载变化等,使得真实波形并非严格意义上的正弦波,Newton-Leibniz公式失去作用。
通常采用Newton-Cotes公式计算积分近似值来解决上述问题,因为高阶公式具有不稳定性,但低阶公式求积精度不高,因此采用复化求积法,即在小区间上采用低阶求积公式,本文选择二阶Newton-Cotes公式的Simpson公式来求积分。
复化求积公式是在小区间上进行的,可以将求积区间长度定义为信号采集窗口的长度,窗口长度由式(3)定义。
式中:Fs为采样频率(1 kHz);Ff为系统的基频(50 Hz)。
将一个周期采集到的数据放入矩阵(4),随着时间的增加,窗口往前移动,矩阵包含数据不断更新,由矩阵包含的值计算任意时刻窗口对应区间的积分。
以时间为横坐标,设任意时刻的积分区间为[a,b],将其划分为2n等份,分点xk=a+kh,h=,k=0,1,2,…,n,在每个小区间[x2k,x2k+1](k=0,1,…,n-1)上采用Simpson公式,利用复化Simpson公式在每个区间求得的积分SI表达式如下:
1.2 故障检测算法
由图1所示电流波形可知,系统正常运行时,电流波形在时间轴上的积分接近于0,随着时间的推移,窗口移动到故障区域,此时电流在时间上的积分不再等于0,因此,可以考虑将电流信号在一个周期的积分作为判断振荡和故障的指标值。所提出的算法如图2所示。
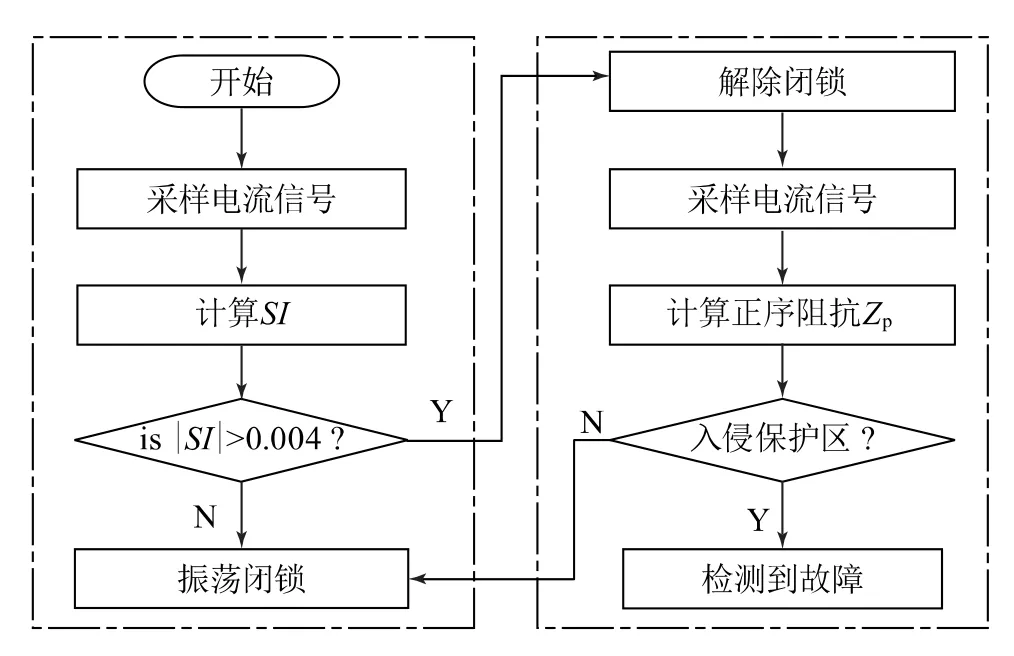
图2 距离保护振荡闭锁逻辑
2 仿真和测试
为验证所提方法的正确性,考虑使用Matlab对四机两区域的系统进行仿真。该网络由4台发电机和11条母线组成,其单线图如图3所示。在7号母线上安装了距离继电器以保护1号线,引起线路1振荡的故障在线路4上产生,对获得的电流信号进行处理以获得SI值,距离保护闭锁和解闭锁通过图2所示算法实现。
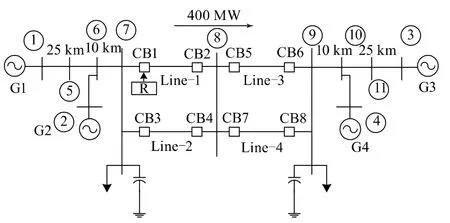
图3 仿真系统结构图
2.1 稳定的振荡
为了模拟Line-1上的稳定振荡,考虑在1 s时断开Line-4上两端的断路器。图4(a)和(b)显示了3台发电机的功率和转子角速度的变化,振荡不会使它们脱离同步速度,所以这是一个稳定的振荡。图4(c)显示了G2、G3和G4相对于G1的转子角,在振荡期间,相对角增加,然后在一定范围内开始振荡。
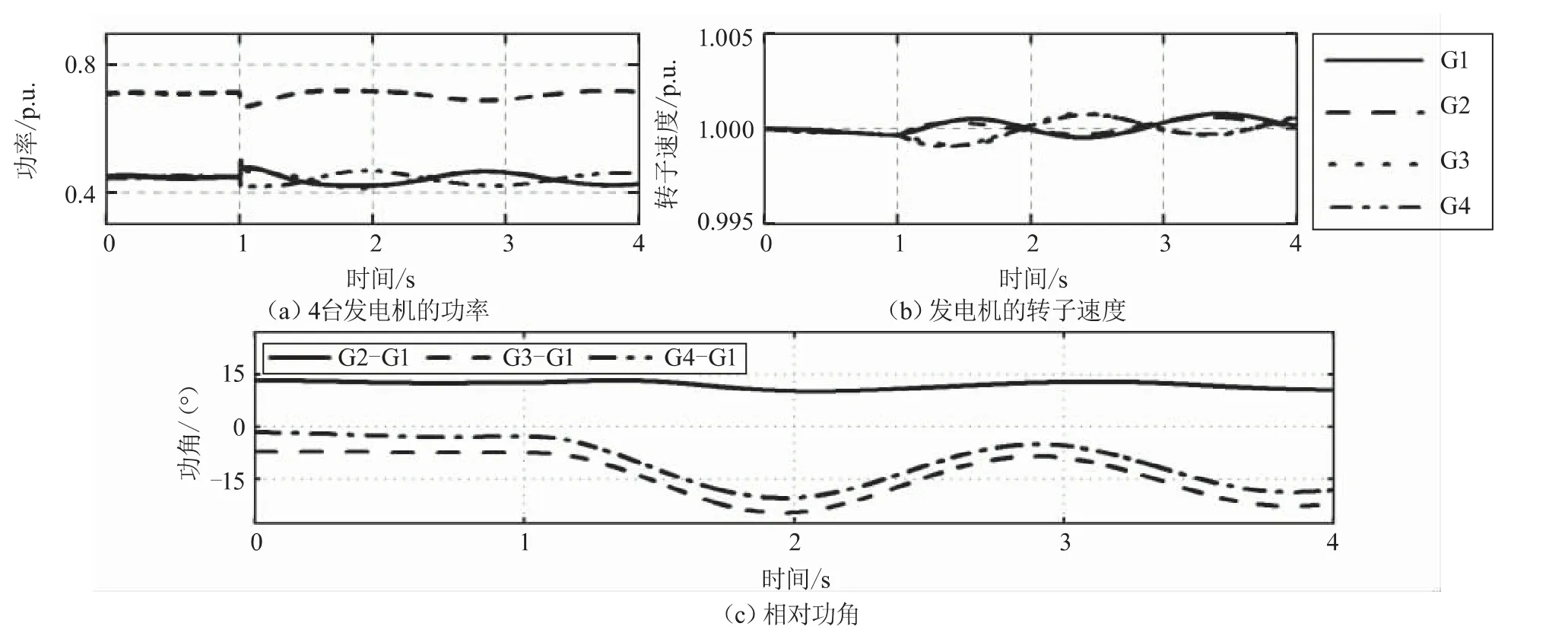
图4 稳定振荡条件下的发电机性能
图5(a)显示了此时的电流波形。对线路1获取的电流信号进行处理获得SI波形,图5(b)为所提算法的SI值,在1 s时,由于线路4的断开,从线路1得到的SI值达到峰值,随后线路经历振荡。由图5(c)可知,继电器观测到的阻抗在1.708 s入侵动作区域,但SI值低于阈值,所提方法检测到振荡并闭锁距离保护,防止了继电器错误动作。
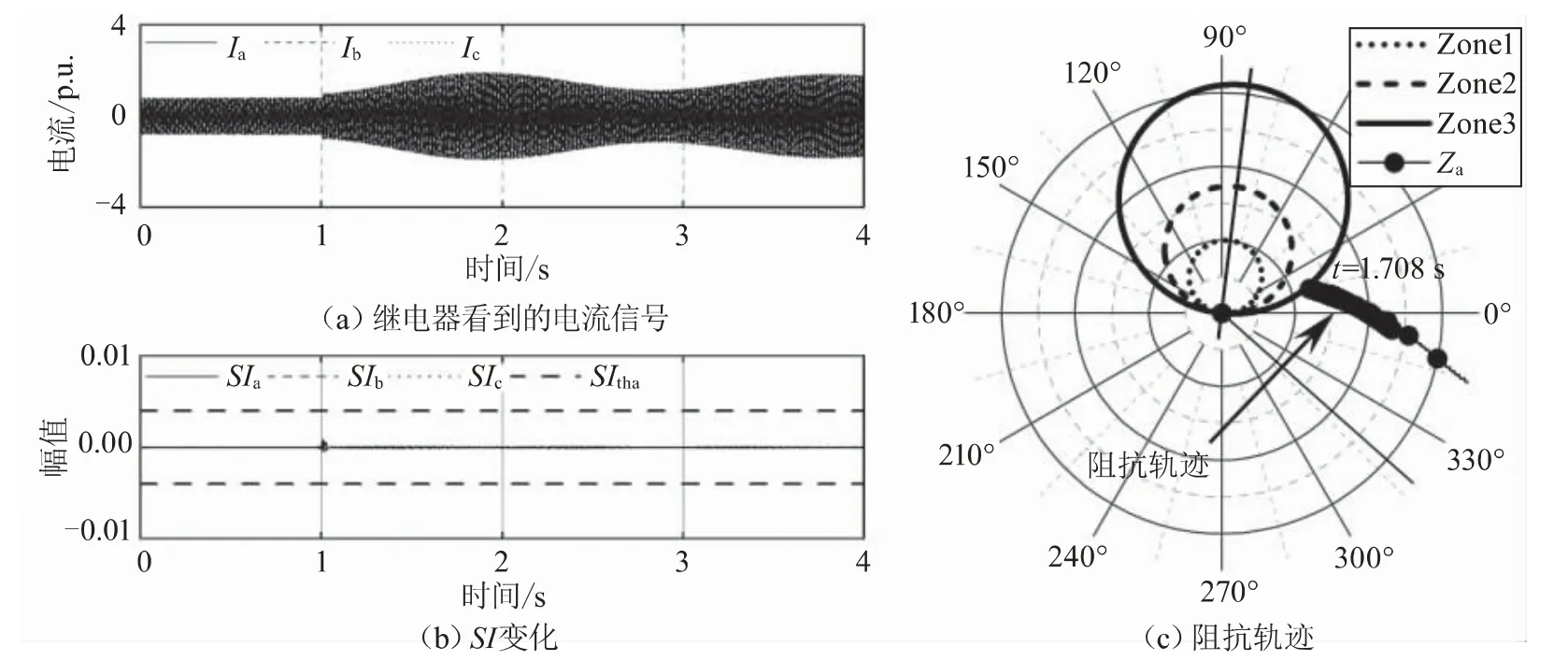
图5 所提算法在稳定的功率振荡下的性能
2.2 不对称的振荡
电力系统的情况很复杂,受其他线路的影响产生的振荡并不总是对称的。对于电压等级较低的线路,在发生故障时,为了方便,可以直接断开三相线路,在电压等级较高的情况下,会出现断开故障相的情况,当单相线路被切换或断开时,会在相邻的线路产生不对称的振荡。为了研究所提出的方法在这种情况下的性能,在0.2 s时施加一个单相故障(A-G),500 ms后断开A相两端的断路器。所提算法的性能如图6所示,在A相上产生了非对称PS,B相和C相也受到了微弱的影响,在非对称PS期间,相应的三相SI值没有超过阈值,所提算法仍然表现良好。
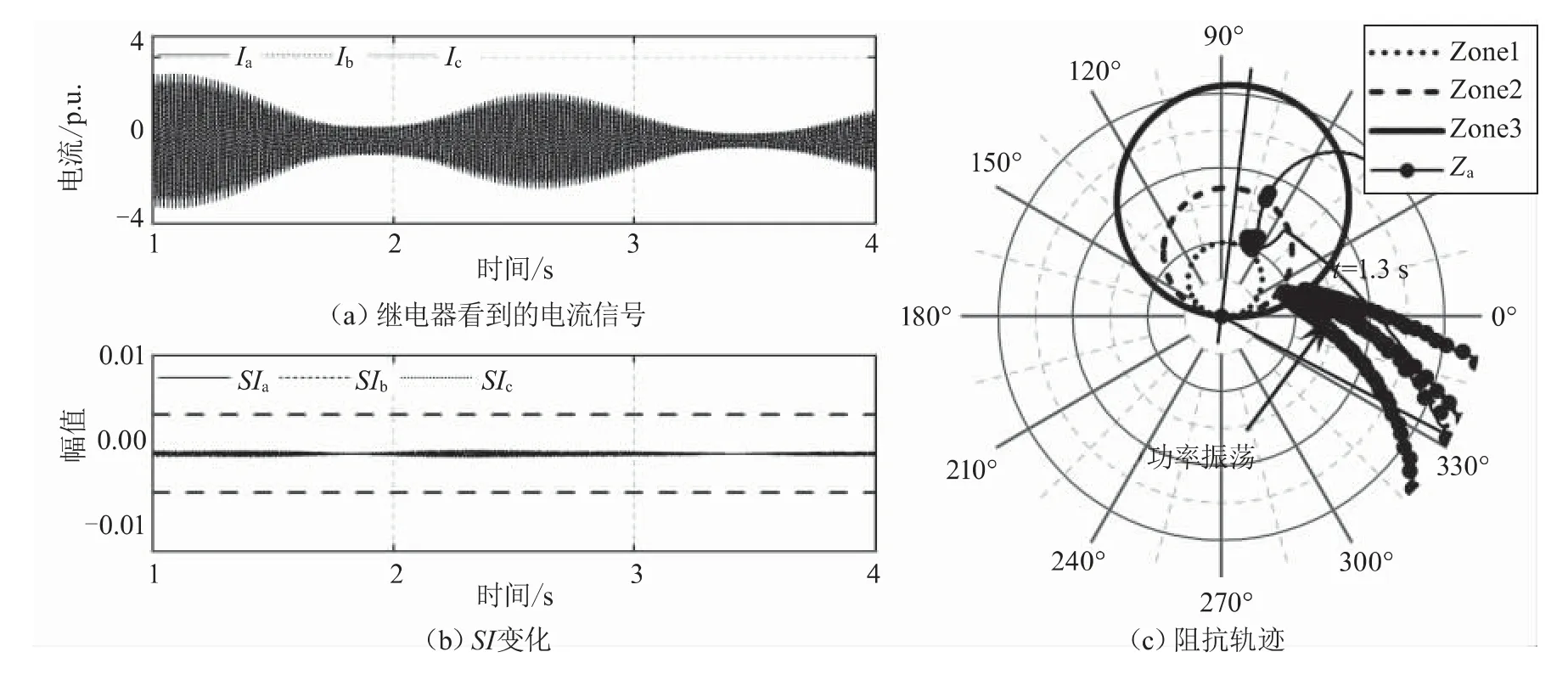
图6 所提算法在不对称的功率振荡下的性能
2.3 不稳定的振荡
线路4在0.2 s时出现故障,500 ms后,两端断路器断开以清除故障,由于故障持续时间的增加,在线路1上产生了振荡,这种振荡可以被其上的继电器检测到,由于引起振荡的故障持续时间长(断路器没有及时清除故障),发电机转子在过剩转矩的作用下不断加速,最终失去与其他发电机的同步速度,这种情况下的振荡,称为不稳定的振荡。图7(a)和(b)显示了这种情况下4台发电机的功率特性、转子角速度特性,图7(c)显示了G2、G3和G4相对于G1的功角。
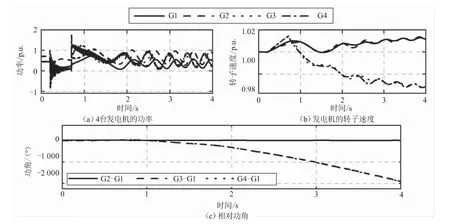
图7 不稳定振荡条件下的发电机性能
在失步的情况下,输电线路跳闸有利于线路从不稳定到稳定的过渡,但跳闸需要根据系统的复杂性,由失步继电器跳闸,距离继电器应能识别不稳定的振荡。图8显示了所提算法在不稳定振荡下的表现,与其他振荡相比,不稳定振荡期间SI值有明显增加,但仍在上下限阈值内,因此算法在不稳定振荡期间仍能保持继电器为闭锁,不会出现误操作。
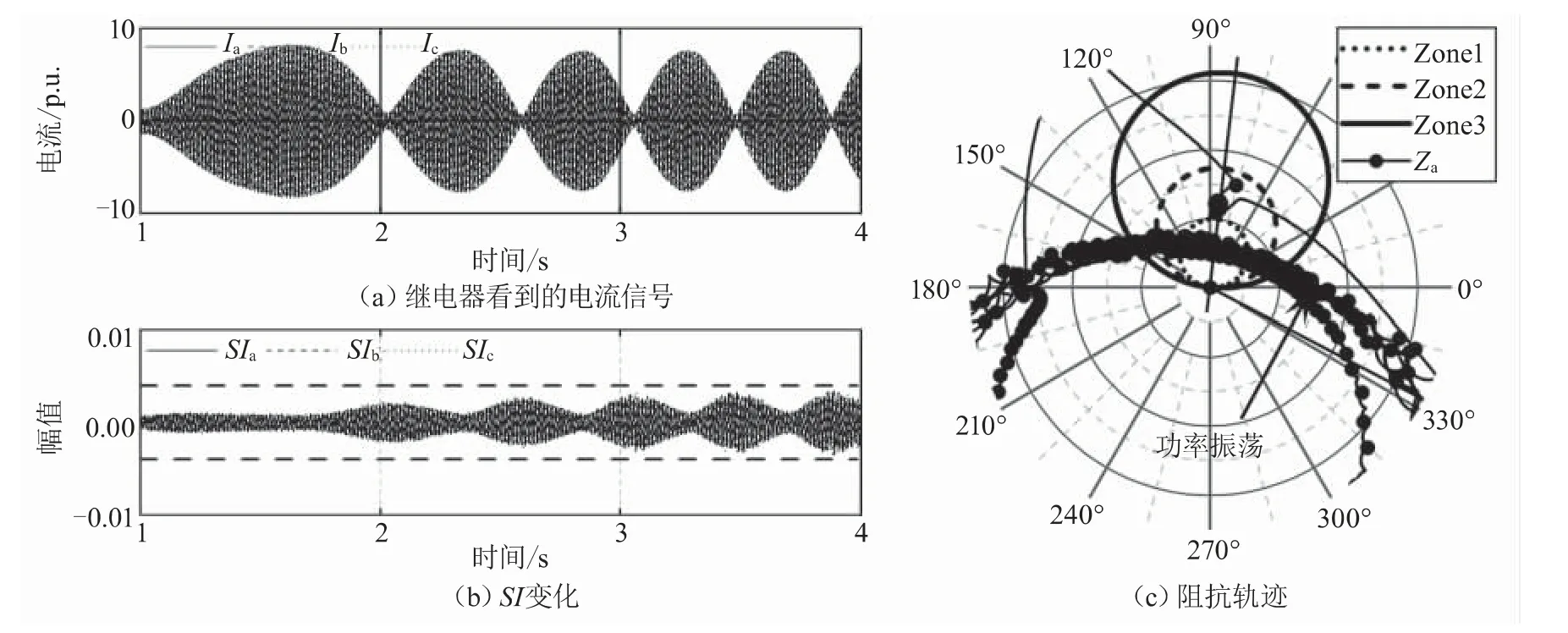
图8 所提算法在不稳定的功率振荡下的性能
2.4 振荡期间发生故障
本节评估了所提方法在系统振荡期间通过创建再故障场景来测试解除闭锁的能力,测试结果如表1所示,变量涉及振荡和故障,考虑快速和慢速振荡的影响,对于不同振荡周期的对称振荡,故障对所提方法的影响反映在故障电阻、位置和功角上,通过改变这些参数进行了相关场景的测试。
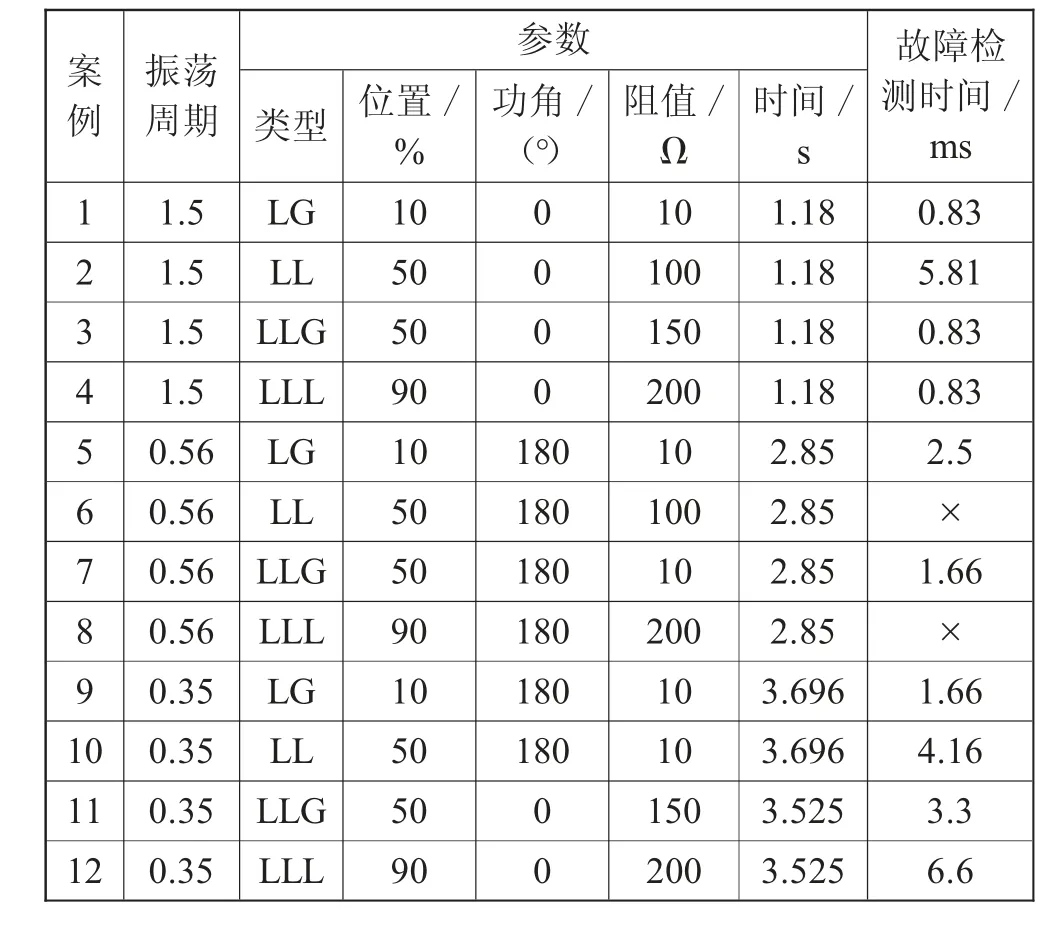
表1 不同振荡场景下发生故障时所提方法的检测时间
由表1可知,振荡期间发生故障时,所提算法可以快速解开继电器距离保护的闭锁,虽然存在两个失败案例,但这种情况在实际电力系统中发生概率很小,对于大多数测试场景,所提方法仍能提供有效决策。
3 结束语
本文提出了一种改进距离保护的新方法来检测振荡和振荡期间发生的故障。提出的指标SI值是电流信号在时间轴上的积分值,振荡期间发生故障时,SI值发生显著变化,这足以区分振荡和故障,它精确地放大了振荡和故障之间的差异,使得通过设定一个阈值来区分两者成为可能。该方法在两区四机网络中进行了模拟,分别讨论了振荡期间发生的故障,通过设置不同的故障类型、阻抗值、功角和位置进行多组试验,结果表明该方法具有良好的性能,响应速度快,并且计算负担较小,数学逻辑简单,这使得该方法易于实施。
