某体育场大跨拱形雨蓬加固改造设计与分析

2023-10-25徐旭锋王正刚肖志斌

建筑结构 2023年20期

徐旭锋, 王正刚, 肖志斌, 沈金

(浙江大学建筑设计研究院有限公司，杭州 310028)

0 引言

为了满足人们对于大跨度建筑的需求,拱结构因其受力合理,结构简单,施工方便等优点获得了广泛的应用［1］。钢管拱桁架是一种常用的拱结构形式,是钢管通过相贯节点而形成。其受力特性主要是以受压和受弯为主,而其表现出的稳定性问题较为复杂,是拱形钢结构设计的要点［2］。大跨度屋盖结构对风荷载较为敏感,合理考虑风荷载效应是结构设计中的重要一环。《建筑结构荷载规范》(GB 50009—2012)［3］和《拱形钢结构技术规程》(JGJ/T 249—2011)［4］对大跨度拱结构的风荷载的取值参考较少,因此本工程进行了数值风洞试验,并为类似抗风的工程设计提出了建议。此外,本文主要从结构静力计算、位移变形、稳定性分析、抗连续倒塌性能分析、支座位移分析、关键节点分析等方面对某大跨拱形雨蓬结构进行了分析和研究。

1 工程概况

本项目为合肥一中体育场,位于安徽省合肥市湖滨新区,原体育场钢结构雨蓬腐蚀严重,存在一定安全隐患,因此对旧雨蓬进行拆除,并在原看台上新建拱形雨蓬,建筑效果图见图1。该钢结构雨蓬长159.6m,宽18m,高19.5m。

图1 雨蓬建筑效果图

本项目的结构设计使用年限为50年,安全等级为一级。结构的抗震设防类别为重点设防类(乙类),抗震设防烈度为7度,设计基本地震加速度为0.10g,设计地震分组为第一组,建筑场地类别为Ⅱ类,特征周期0.35s。此结构为大跨轻质钢结构,对风荷载和雪荷载敏感,因此取100年一遇风压0.4kN/m2和雪压0.70kN/m2。钢结构合拢初始温度区间为15～25℃,考虑合肥市的极端气温,因此温度作用标准值取升温35℃,降温-45℃。

2 钢雨蓬结构体系及抗震性能化目标

2.1 钢雨蓬结构体系

根据建筑方案,本雨蓬结构可以分为主拱结构、次结构和纵向附加结构,如图2所示。主拱结构由两榀钢管拱桁架、横向支撑和斜撑组成,横向支撑包括5榀立体桁架、4榀平面桁架和2榀空间桁架,以满足看台雨蓬的承载力和变形要求。次结构由一根主杆和若干撑杆组成,其与主拱结构紧密连接,共同受力。纵向附加结构为两段三角形截面立体桁架。次结构及纵向附加结构用于满足看台雨蓬的造型要求。主拱结构的跨度为128m,矢高为18m,矢高比为0.14,主拱结构构件为管桁架,截面为矩形,截面宽度为2.5m,截面高度为2.8m,两榀拱中心线间距15.5m。主拱结构立面按合理拱轴线布置,拱底悬链线标准方程［5］为:

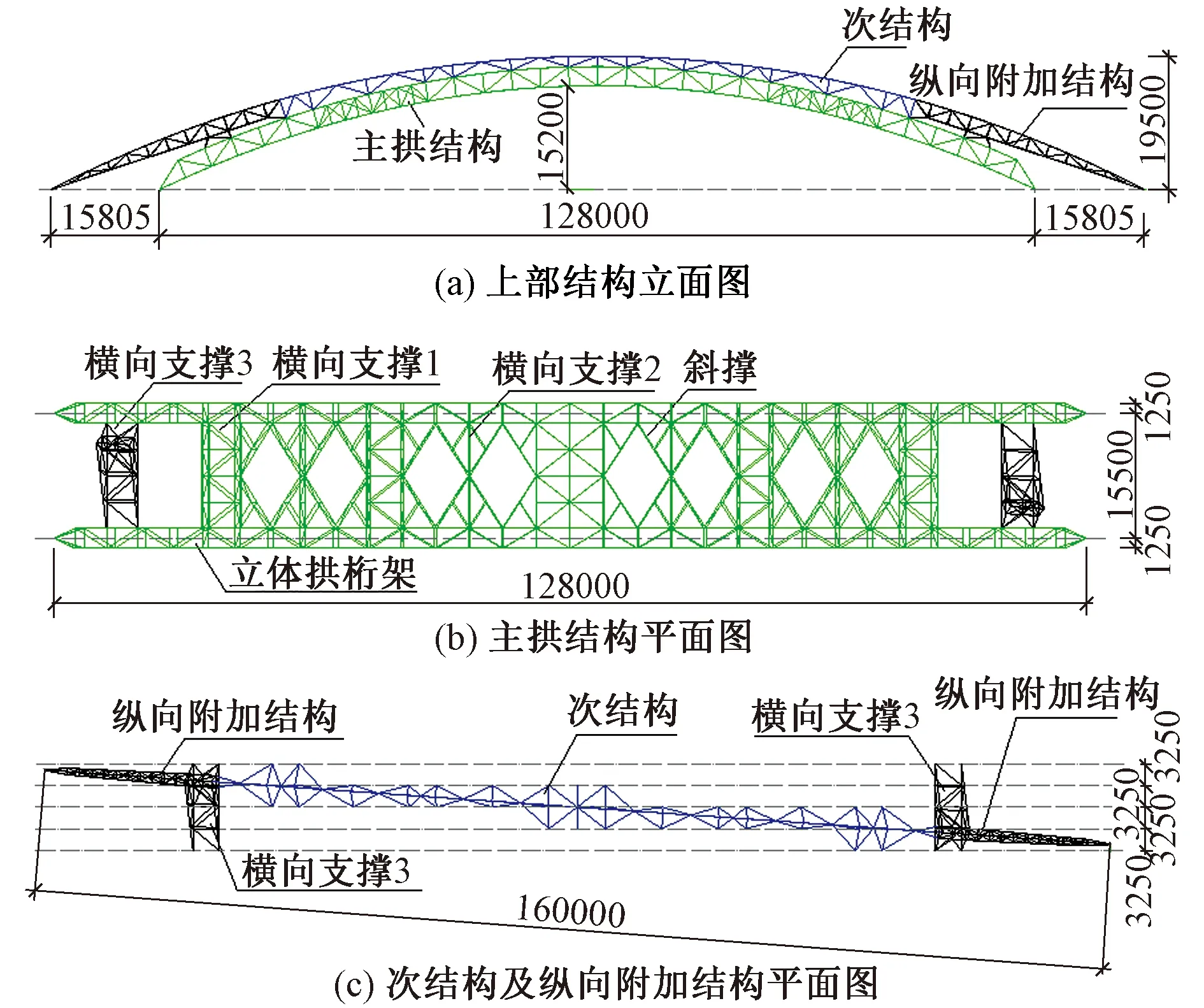
图2 结构受力体系图

y=acosh(x/a)+b

(1)

式中:a为缩放系数;b为竖向位移。

代入本工程,可求得a=-137.2m;b=152.4m。

2.2 抗震性能化目标

根据《超限高层建筑工程抗震设防专项审查技术要点》(建质﹝2015﹞67号)［6］规定,本项目为跨度超限结构。参考《高层民用建筑钢结构技术规程》(JGJ 99—2015)［7］,结合工程抗震设防类别、设防烈度、场地条件、结构特殊性、建造费用、震后损失和修复难易程度等因素,按B级抗震性能目标进行设计,即多遇地震下达到性能水准1,设防烈度下达到性能水准2,预估的罕遇地震下达到性能水准3。具体性能状况要求如表1所示。

表1 结构构件抗震性能目标

3 数值风洞试验结果

3.1 基本理论

随着计算机硬件水平的不断提高以及计算流体动力学(computational fluid dynamics,CFD)技术的成熟发展,采用CFD技术对建筑风场进行数值模拟已经成为预测建筑物风效应的一种新型有效方法。相比于进行风洞试验, 这种技术可以用较少的费用和较短的时间获得相应的研究结果［8］。

本工程基于雷诺平均Navier-Stokes(N-S)方程和亚格子模型的大涡模拟(large eddy simulation, LES)湍流模型方法,采用FLUENT中的速度进口边界条件(velocity-inlet),对结构进行了数值风洞模拟。场地采用B类地貌,粗糙度系数取α=0.15,在0°～360°范围内每隔30°取一个风向角作为一个工况计算,总共有12个计算工况,如图3所示。

图3 计算风向角示意图

参考文献[8-10]及相关数值风洞试验报告［11］,对数据进行处理以得到所需的参数,结构表面某点i的风压系数Cpi及体型系数μsi的计算如下:

Cpi=(Pi-P∞)/(0.5ρV∞2)

(2)

μsi=Cpiμzr/μzi

(3)

式中:Pi为测点i的净风压值;P∞为参考点静压力值;ρ为空气密度;V∞为参考点的风速;μzr为试验时参考风速点的高度;μzi为测点i的风压高度变化系数。

各分块体型系数可按式(4)进行计算:

(4)

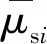
根据工程实际,结合荷载风振系数(式(5))和位移风振系数(式(6)),采用有限元时程分析得到的加速度均方根计算结构的最大惯性力,并以经折减的脉动风压均方根来考虑结构的最大背景风振力,一致风振系数进行简化处理,如式(7)所示。

(5)

(6)

(7)

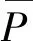
3.2 体型系数和风振系数

每个分块都包含有多个风压探测点,每个风压探测点都可以求出一个相应的风压系数和体型系数,将每个分块中的各个探测点求得的风压系数进行面积加权平均值计算,作为该分块的体型系数,从而保证分块体型系数结果的合理性。考虑到此结构为中心对称,因此仅列出0°、30°、60°、90°、300°和330°风向角下的结构体型系数和一致风振系数,见图4,其中括号内为一致风振系数。

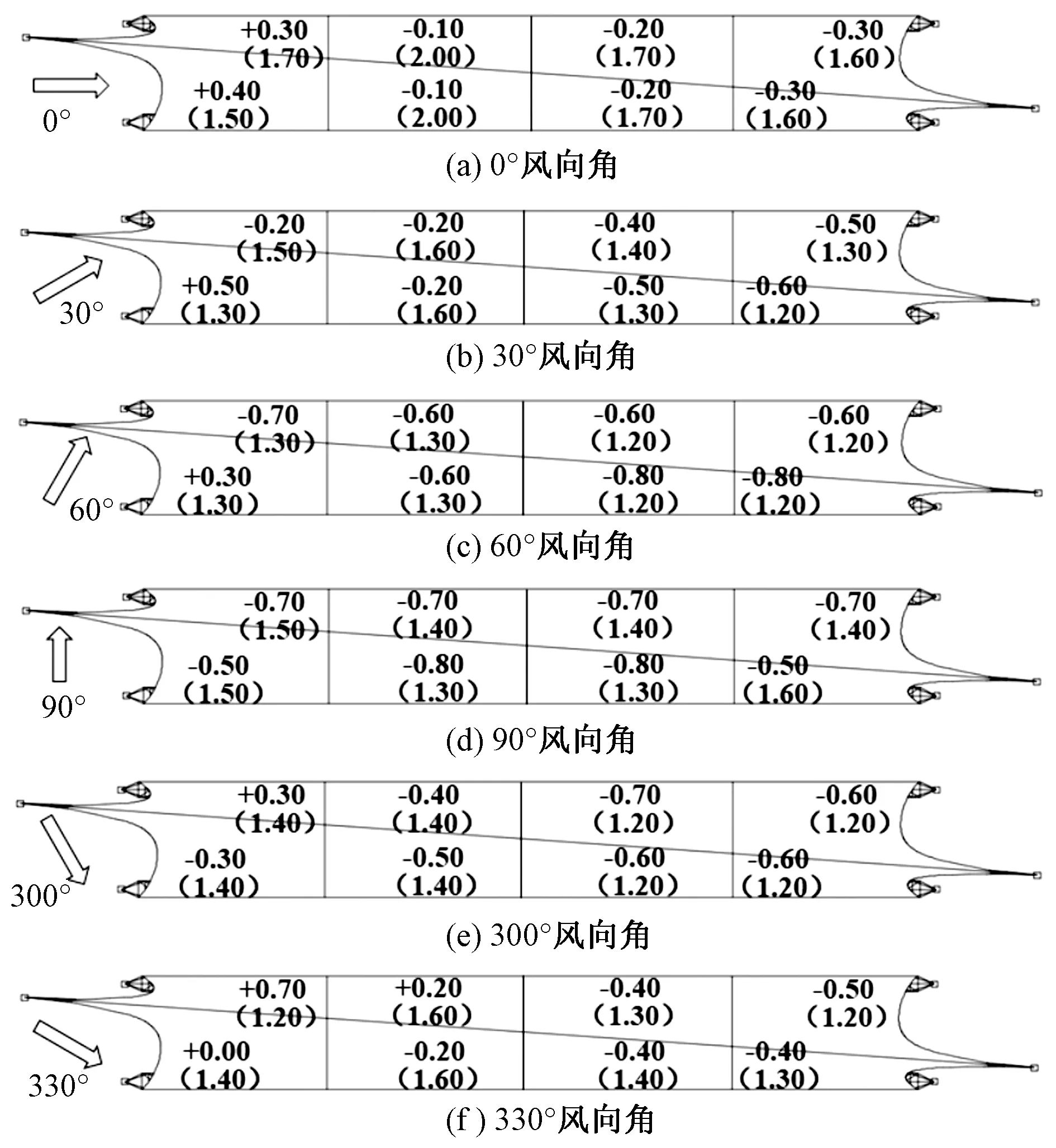
图4 各风向角下结构体型系数和一致风振系数

3.3 结果对比

《建筑结构荷载规范》(GB 50009—2012)给出了四面开敞式双坡屋面的体型系数,如图5(a)所示。文献[8]给出了开敞式单跨拱形屋面体型系数,并按线性内插得到矢高比为0.14时的屋面体型系数,如图5(b)所示。

图5 文献相关体型系数图

结合建筑物立面以及数值风洞试验结果,风向角对结构的体型系数和风振系数均有较大的影响。在0°风向角下,体型系数数值变化规律与开敞式单跨拱形屋面体型系数相似,在90°风向角下,体型系数数值变化规律与开敞式双坡屋面体型系数相似。但是考虑到此结构的横向跨度较小,且中间有凸起,因此数值风洞试验得出的体型系数较小。对比图4和图5,可以发现数值风洞试验得出的体型系数变化规律和《建筑结构荷载规范》(GB 50009—2012)及文献[8]基本一致,但数值有较大差异。

结构设计时,需对多种风荷载工况进行包络设计,且本结构对风荷载敏感,风压时正时负,应考虑体型系数变号的可能情况。

《拱形钢结构技术规程》 (JGJ/T 249—2011)中对于中小跨度拱形钢结构可采用平均风荷载乘以风振系数的方法近似考虑结构的风动力效应,风振系数参考取值为1.2～1.8。由图4可知,各风向角下的结构一致风振系数基本都在这个范围内,只有0°风向角下局部有出现2.0的风振系数。为结构安全考虑,本结构整体风振系数取1.8。

4 结构计算分析

4.1 计算模型

上部结构采用3D3S和MIDAS Gen软件进行整体分析,图6为上部结构三维计算模型。主要构件尺寸见表2,主要计算参数和模型假定选取如下:1)阻尼比为0.02;2)考虑竖向地震作用,采用振型分解反应谱(CQC)法对整体模型进行计算;3)弦杆之间采用刚接连接,其余杆件连接采用铰接和刚接节点双控计算;4)主拱支座采用铰接,水平X向、Y向和竖直Z向为刚性约束;5)纵向附加桁架支座采用铰接,水平X向约束释放,水平Y向和竖直Z向为刚性约束;6)采用质量和刚度均退化为零的面单元,施加均布附加恒、活(雪)、风荷载。

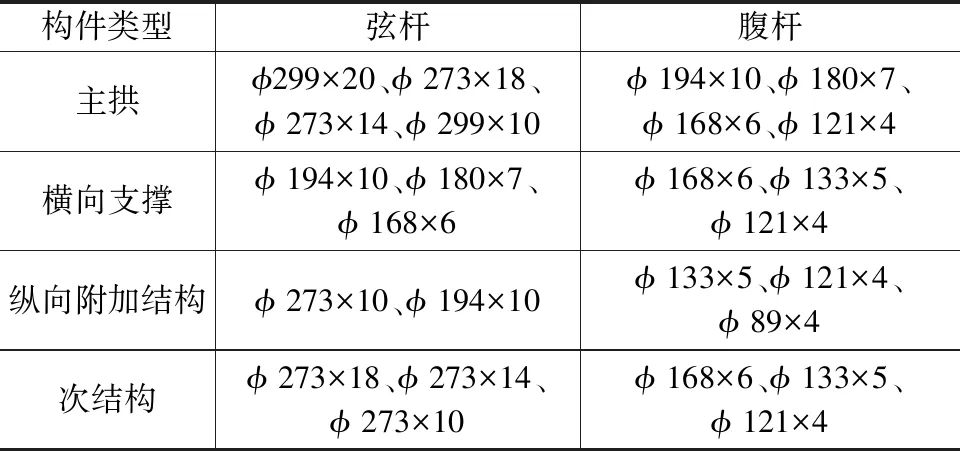
表2 主要构件尺寸/mm

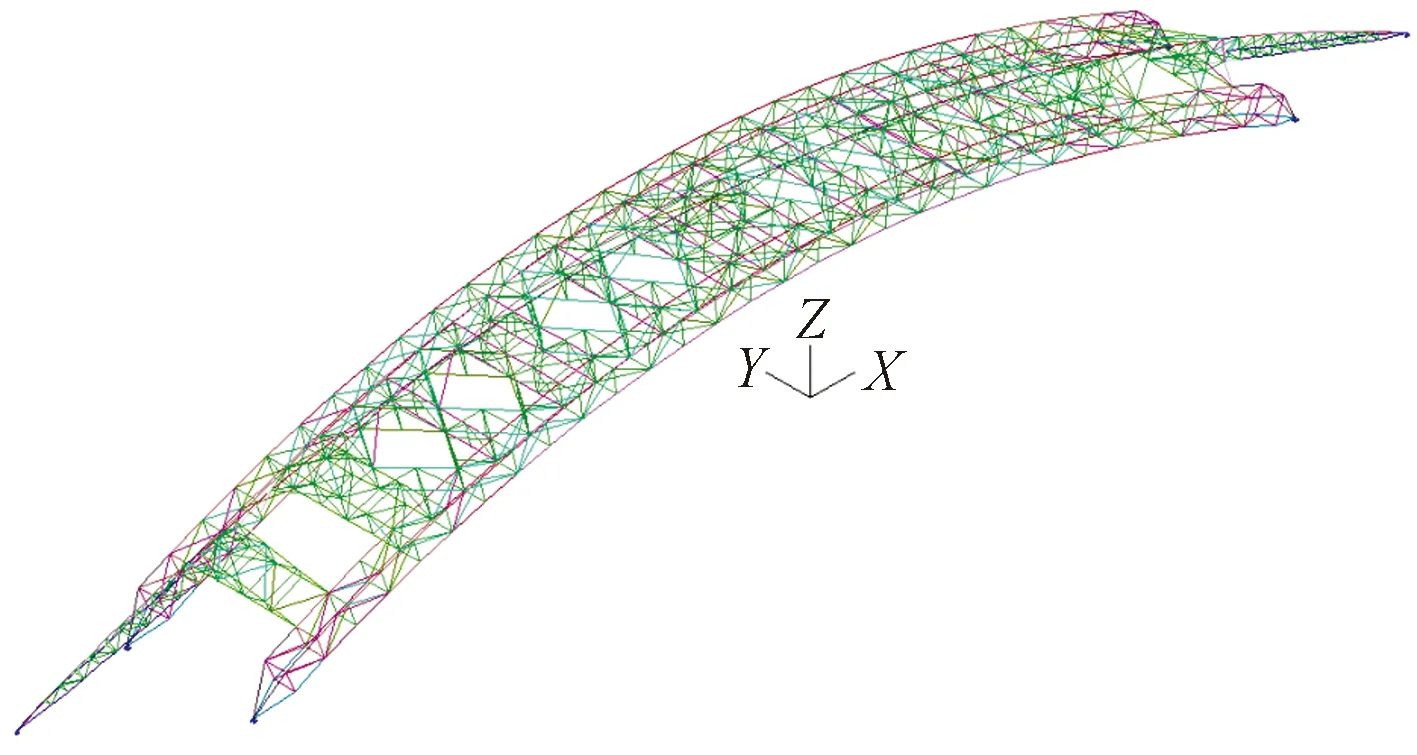
图6 三维计算模型

4.2 结构动力特性

采用3D3S和MIDAS Gen两种软件对结构的动力特性进行对比分析,两种模型的前五十阶振型周期与质量参与系数都非常接近,尤其是结构的几个主要振型模态表现出了一致性。其中,第1阶振型周期为1.03s,以Y向平动为主;第2阶振型周期为0.76s,以X向平动为主;第3阶振型周期为0.67s,以XY向扭转为主;第4阶振型周期为0.46s,以Z向平动为主,如图7所示。

图7 整体模型前四阶振型

4.3 结构承载力分析

对结构主要进行以下荷载组合:1)非地震工况荷载组合(风压为主:1.3恒载+1.05活载+1.5风荷载+0.9温度荷载;风吸为主:0.9恒载+1.5风荷载+0.9温度荷载)。2)地震组合(水平地震为主:1.3恒载+0.65活载+0.28风荷载+0.5竖向地震+1.4水平地震作用;竖向地震为主:1.3恒载+0.65活载+0.28风荷载+1.4竖向地震+0.5水平地震作用)。

非地震工况荷载组合下杆件稳定应力比计算结果如图8所示。由图可得,非地震工况荷载组合下,对于关键杆件的稳定应力比最大值为0.79,对于一般杆件的稳定应力比最大值为0.83。

图8 非地震工况荷载组合下杆件稳定应力比分布图

4.4 结构位移分析

图9(a)为结构在荷载标准组合(1.0恒载+1.0活载)下的变形云图,由图可得,拱顶最大竖向变形为65mm,小于L/400=320mm (L为拱桁架结构的跨度,L=128 000mm),满足《钢结构设计标准》 (GB 50017—2017)［12］相应要求。在横向方向上,相对竖向变形值为66-65=1mm,小于L′/400=39mm (L′为两榀拱桁架结构的间距,L′=15 500mm),满足规范要求。同时,根据分析结果,在1.0活载作用下,结构最大竖向变形值为37mm,满足规范L/500的要求。

图9 结构在不同荷载组合下的竖向变形/mm

图9(b)为结构在风荷载组合(0°风向角下的1.0风荷载)下的变形云图,由图可得,结构最大竖向变形值约为61mm,满足规范L/500的要求。图9(c)为结构在风荷载组合(90°风向角下的1.0风压荷载)下的变形云图,由图可得,结构最大竖向变形值约为49mm,满足规范L/500的要求。图9(d)为结构在风荷载组合(90°风向角下的1.0风吸荷载)下的变形云图,由图可得,结构最大竖向变形值约为46mm,满足规范L/500的要求。

4.5 小震弹性时程分析

小震弹性时程分析计算采用MIDAS Gen软件。地震时程采用两组天然波(TH1、TH2)和一组人工波(RH1),按主向、次向、竖向加速度1∶0.85∶0.65比例输入,加速度峰值调整到55gal。地震作用下时程分析结果与CQC法结果的基底剪力对比如表3所示。由表可得,3组地震波时程计算所得的基底剪力平均值不小于CQC法计算结果的80%,且不大于CQC法计算结果的120%,满足《建筑抗震设计规范》(GB 50011—2010)(2016年版)［13］设计要求。该结构在X向的地震响应放大系数为1.16,在Y向的地震响应放大系数为1.20。在计算地震作用下的结构变形及构件承载力时均需考虑此放大系数。

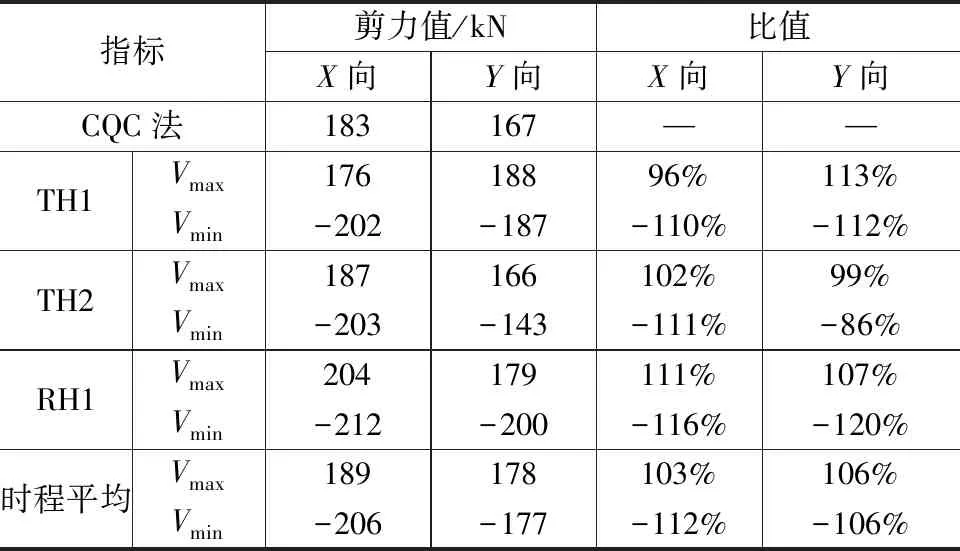
表3 时程分析结果与反应谱结果基底剪力对比

主拱结构拱顶节点在三条地震波作用下的竖向加速度及位移时程响应如图10所示。由图可以发现,在TH2地震波作用下,主拱结构拱顶节点的竖向加速度时程响应峰值为1 142mm/s2,较输入地震波峰值放大了2.1倍。结构最上方的节点的竖向位移峰值为8.3mm,对结构影响不大。

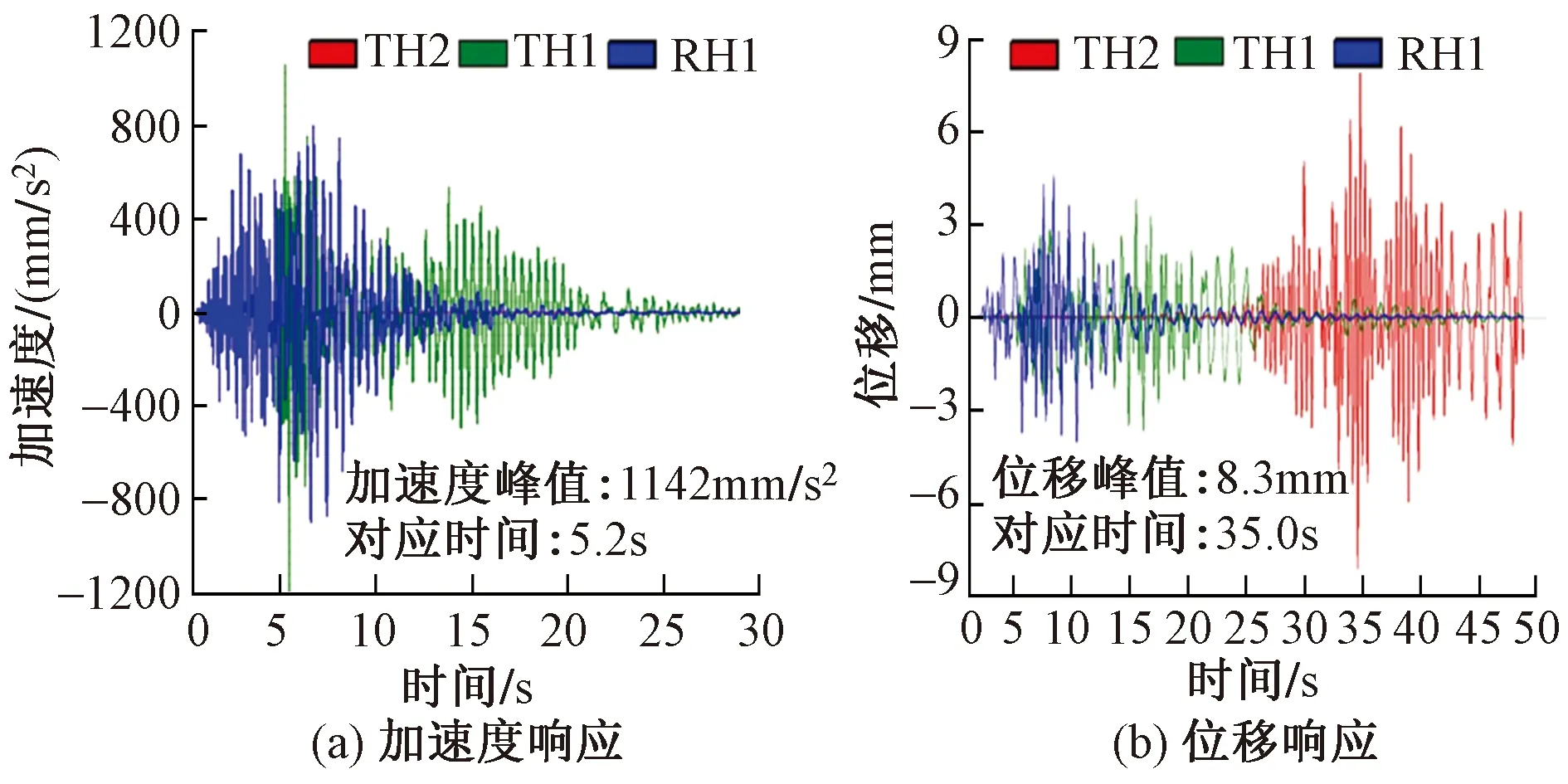
图10 三条地震波作用下主拱结构拱顶节点Z向加速度与位移响应

结合地震响应放大系数,在小震组合作用下,绝大部分钢结构杆件应力比在0.3以下;中震组合作用下,绝大部分钢结构杆件应力比在0.4以下;大震组合作用下,绝大部分钢结构杆件应力比在0.5以下。说明地震作用对此结构体系不起控制作用。

4.6 结构稳定性分析

使用3D3S软件进行非线性稳定性分析时,根据《空间网格结构技术规程》 (JGJ 7—2010)［14］,需考虑初始几何缺陷、几何非线性及材料非线性,采用von Mises屈服准则,取钢材的屈服强度为345N/mm2,不考虑硬化。初始几何缺陷分布可采用结构的第一阶屈曲模态,其缺陷最大计算值可按主拱跨度的1/300确定［15］。安全系数K为结构发生屈曲时的极限承载力除以结构稳定容许承载力(荷载取标准值),当按弹性全过程分析时,K可取为4.2。

计算结果表明,在1.0恒载+1.0活载工况下,结构安全系数K=12;在1.0恒载+1.0半跨活载工况下,结构安全系数K=8.8,均满足《空间网格结构技术规程》(JGJ 7—2010)要求。

4.7 结构抗连续倒塌分析

根据《高层民用建筑钢结构技术规程》 (JGJ 99—2015)对本结构采用拆除构件法进行抗连续倒塌分析,拆除后剩余构件承载力应符合下式要求:

Rd≥βSd

(8)

Sd=ηd(SGk+∑ψqiSQi,k)+ψwSwk

(9)

式中:Sd为剩余结构构件效应设计值;Rd为剩余结构构件效应设计值;β为效应折减系数,对中部水平构件取0.67,对其他构件取1.0;ηd为竖向荷载动力放大系数,取2.0。

构件承载力计算时,钢材正截面强度取标准值的1.25倍,斜截面强度取标准值［16］。

选取拱桁架靠内侧的一榀中内力最大的一根斜腹杆进行拆除,拆除位置如图11(a)所示。图11(b)为分析结果,可知剩余结构杆件的最大应力比为0.98,表明该结构体系具有较好的承载潜力,满足结构抗连续倒塌要求。

图11 结构抗连续倒塌分析图

4.8 支座位移分析

考虑到在实际工程的使用过程中基础或者地质的变形会引起支座的位移,本节强制对结构一侧的支座施加20mm的水平位移或者10mm的竖向位移,分析了支座位移对整体结构的影响。

图12、13为结构支座强制位移加载示意及变形分析图。由图13可得,当施加水平位移时,结构主拱顶最大竖向位移值约为29mm;当施加竖向位移时,结构拱顶最大水平位移值约为13mm。由计算分析结果发现,施加水平位移时,支座最大竖向力为5kN,最大水平力为24kN,杆件最大轴力为84kN;施加竖向位移时,支座最大竖向力为2kN,最大水平力为1kN,杆件最大轴力为29kN。总体而言,少量的支座位移对结构整体影响不大。

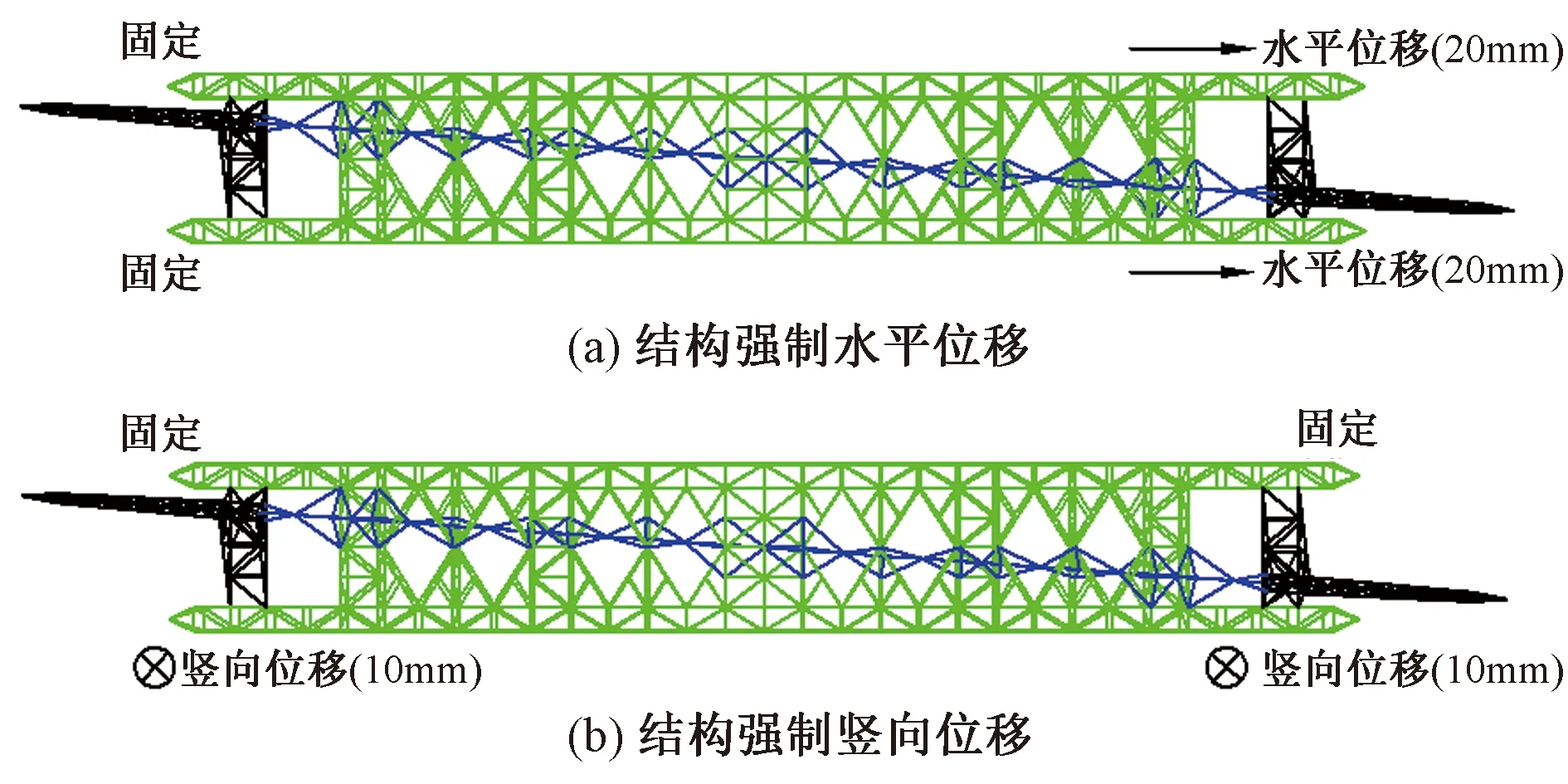
图12 结构支座强制位移加载示意图

图13 结构支座强制位移后主拱变形图/mm

4.9 关键节点分析

在钢管拱桁架的支座处,四根弦杆最终合并为一处,因此弦杆变折处和支座是本项目中的关键节点,节点采用焊接空心球节点,空心球直径为700mm,内设加劲板。本项目采用ANSYS进行节点的计算分析。节点验算采用von Mises强度准则,采用solid95单元模拟钢材,钢材的弹性模量2.06×105N/mm2,泊松比0.3,强化段弹性模量2 060N/mm2,屈服强度345N/mm2。

结合实际工程节点受力情况,将弦杆一端边界按固定端约束,弦杆另一端施加只允许杆件轴向位移的滑动支座,腹杆主要承受轴力作用,因此也施加允许杆件轴向位移的滑动支座。在有限元模型中为更方便地约束杆端位移,在划分网格后,各杆端约束以节点约束的方式施加在杆端截面所有节点上。在计算模型中,杆件长度太长将导致杆件弯曲破坏,且划分单元数过多会降低计算效率,而杆件长度过短会使杆件出现明显的凹凸变形。因此,各杆件长度取杆件直径的五倍,并在杆件外端施加轴力和弯矩［17］。

三种关键节点的构造(图14)及其应力分析结果见图15。上弦杆弯折处节点最大应力为290N/mm2,发生在与腹杆与焊接球连接处;下弦杆弯折处节点最大应力为338N/mm2,也发生在与腹杆与焊接球连接处;支座处节点最大应力为316N/mm2,发生在焊接空心球与支座加劲肋接触区域。由计算分析结果可知,各关键节点应力均没有超过钢材的屈服应力345N/mm2,节点具有足够的强度保证结构安全。