铜尾矿混凝土力学性能的数值模拟

2023-10-25叶晓冬杨忠祥彭苗苗

建材与装饰 2023年31期

叶晓冬，杨忠祥，彭苗苗

（滇西应用技术大学，云南大理 671000）

0 引言

铜尾矿是铜矿产业工业废弃物中相当重要的组分，它是通过矿石选矿，获取有用矿物之后的废弃物。2021 年，我国尾矿产量在13.08 亿t 左右，铜尾矿产量3.34 亿t[1]。在产量巨大的同时，铜尾矿的综合利用率仅为8%左右[2]。对于铜尾矿的处理，我国大多采用露天干堆，因占据大量农田，保守估计每年造成的经济损失为105 亿元[3]，同时尾矿坝存在着一定的溃坝风险。因此，提高铜尾矿的利用率十分必要。

铜尾矿作为建筑材料可以起到绿色、环保、节能的作用，有较好的经济效益，符合我国发展低碳经济的发展方向。目前已有学者及工程技术人员进行了一定研究：方永浩等[4]发现铜尾矿可作为蒸压砂砖原料，且该砂砖力学性能良好。邹先杰等[5]发现铜尾矿作为作为混凝土细集料，可改善新拌混凝土的泌水离析性。刘倩等[6]使用铜尾矿制微晶玻璃。刘维平等[7]利用铜尾矿制彩色石英砂。田键等[8]发现铜尾矿制备的砌块最大抗压强度达到5.1MPa，平均抗压强度达到4.7MPa，达到A3.5，B06 的蒸压加气混凝土砌块的要求。

在目前的研究中，对铜尾矿混凝土力学性能的研究主要集中在实验研究，数值模拟较少。

使用数值模拟能够更高效、更便捷地预测混凝土强度，因此，本文在笔者原有实验数据[9]的基础上利用ANSYS 建立铜尾矿混凝土（铜尾矿掺量为0%、10%、20%）力学模型。分别建立铜尾矿混凝土抗压强度模型、铜尾矿混凝土劈裂抗拉强度模型、铜尾矿混凝土抗折强度模型。将有限元所得结果与实验结果对比，分析其模拟精度。同时将数值模拟的抗压强度结果带入抗压强度与抗拉强度之间的线型回归方程，对比数值模拟与线型预测的精度。

1 实验配合比及实验结果

采用42.5 普通硅酸盐水泥；所用铜尾矿粉来自云南省玉溪市大红山龙都尾矿库，铜尾矿粉密度2.97g/cm3，平均粒径0.0188mm。

所用水为试验室的自来水；粗骨料为机轧碎石，粒径范围5～25mm，符合《建设用碎石卵石》（GBT 14685—2011）要求。

试验使用人工砂，细度模数3.4，属于粗砂，Ⅰ类砂。铜尾矿混凝土配合比如表1 所示。

表1 铜尾矿混凝土配合比

铜尾矿混凝土力学试验结果如表2 所示。

表2 铜尾矿混凝土力学试验结果

2 模型建立

2.1 几何模型及边界条件

铜尾矿混凝土抗压强度模型为与实验室尺寸相同的150mm×150mm×150mm 立方体。并在立方体底面构建硬质垫块，在垫块底面施加固定约束，顶面施加均布荷载。

铜尾矿混凝土劈裂抗拉强度模型为与实验室尺寸相同的150mm×150mm×150mm 立方体。上下设置长150mm 垫条，垫条与模型上下面的中心线对准并与顶面垂直。在下垫条底面施加固定约束，上垫条顶面施加均布荷载。

铜尾矿混凝土抗折强度模型为与实验室尺寸相同的150mm×150mm×550mm 立方体。模拟实验室实际受力状态，支座和加载处共设置4 块垫块。支座底面施加固定约束，加载处施加均布荷载。

2.2 参数设定

垫块均使用solid45 单元，铜尾矿混凝土抗压、劈裂抗拉强度模型中弹性模量3×105MPa，铜尾矿混凝土抗折强度模型中弹性模量0.4×105MPa，泊松比0.3。

混凝土立方体使用solid65 单元，考虑混凝土开裂后的应力释放，张开裂缝的剪力传递系数为0.5，闭合裂缝的剪力传递系数为0.9。泊松比为0.2，弹性模量根据吕德生等[10]研究所得弹性模量与抗压强度时间关系式如式（1）所示。

式中：E——弹性模量，MPa；fcu——混凝土28d 抗压强度，MPa。

混凝土的本构模型使用MKIN 多线性随动模型，考虑混凝土应力应变曲线中的下降段。根据《混凝土结构设计规范》（GB 50010—2010）中应力应变关系输入相应值。

求解设置中，打开自动时间步，最大迭代次数设为60，子步数设为500，最小步数为200。

铜尾矿混凝土抗压强度、劈裂抗拉强度、抗折强度模型中混凝土立方体的网格尺寸均设为50。其网格划分结果分别如图1、图2、图3 所示。

图1 抗压强度模型网格划分结果

图2 劈裂抗拉强度模型网格划分结果

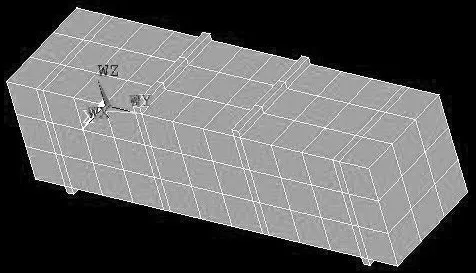
图3 抗折强度模型网格划分结果

3 计算结果及分析

3.1 有限元结果与实验室结果对比

铜尾矿混凝土ANSYS 软件数值模拟结果如表3所示，由表3 可知，对于数值模拟的28d 铜尾矿混凝土抗压强度，随着铜尾矿粉掺量的提升，抗压强度呈现增大的趋势。铜尾矿粉掺量10%与20%时抗压强度基本相同，比未掺铜尾矿时高1MPa 左右。其原因在于铜尾矿粉掺了10%、20%的铜尾矿混凝土弹性模量较未掺铜尾矿的混凝土高。对比实验结果，抗压强度的变化趋势基本相同。当掺量0%，模拟强度较实际值下降2.39MPa、3.2%。当掺量为10%，模拟强度较实际值下降2.93MPa、3.8%。当掺量为20%，模拟强度较实际值下降2.98MPa、3.9%。可见随着铜尾矿掺量提升，抗压强度的模拟值与实际值的偏差也逐渐增大，但是偏差均不大，总体来说铜尾矿混凝土抗压强度模型的精度较高。

表3 铜尾矿混凝土ANSYS 软件数值模拟结果

对于数值模拟的28d 铜尾矿混凝土劈裂抗拉强度，随着铜尾矿粉掺量的提升，劈裂抗拉强度呈现先减小后增大的趋势。当掺量由0%提高到10%，劈裂抗拉强度降低0.64MPa、15.9%。当掺量由10%提高到20%，劈裂抗拉强度提高0.75MPa、22.2%。相对于实验结果的先增大后减小，模拟结果与之存在一定的偏差。当掺量0%，模拟强度较实际值下降0.46MPa、10.3%。当掺量为10%，模拟强度较实际值下降1.46MPa、30.2%。当掺量为20%，模拟强度较实际值下降0.33MPa、7.4%。可见仅掺量10%时偏差较大，因铜尾矿混凝土实际的应力应变曲线与规范所取数值有所差异，导致的模拟精度的下降。

对于数值模拟的28d 铜尾矿混凝土抗折强度，随着铜尾矿粉掺量的提升，抗折强度呈现先增大后减小的趋势。当掺量由0%提高到10%，抗折强度提高0.81MPa、8.6%。当掺量由10%提高到20%，抗折强度降低0.75MPa、6.8%。该趋势与实验结果基本相同，但存在一定偏差。掺量0%，模拟强度较实际值提高0.78MPa、9%。当掺量为10%，模拟强度较实际值提高1.26MPa、14.1%。当掺量为20%，模拟强度较实际值提高0.68MPa、7.7%。可见三组模拟数据与实验结果的偏差并不大，该模型精度较高。

3.2 抗拉强度数值模拟结果与线性回归

笔者在之前关于铜尾矿混凝土的实验研究中，除表2 数据外还得到大量铜尾矿混凝土抗压强度、劈裂抗拉强度、抗折强度数据，通过线性回归的方法，将抗压强度与劈拉强度关系以及抗压强度与抗折强度的关系进行总结，分别如式（2）和式（3）所示。

式中：ft，s——铜尾矿混凝土28d 劈裂抗拉强度，MPa；ft，f——铜尾矿混凝土28d 抗折强度，MPa。

将数值模拟的抗压强度结果带入式（2）和式（3），可得线性预测结果如表4 所示。

表4 线性预测结果

由表4 可见，随着掺量变化，混凝土的劈裂抗拉强度未发生明显变化，均集中在4.4MPa，抗折强度也未发生明显变化，均集中在7.81MPa。其原因在于铜尾矿混凝土抗压强度数值模拟的结果在不同铜尾矿掺量下差异不大。

将线性预测结果与数值模拟结果对比，可见0%、10%、20%铜尾矿掺量下，线性预测的劈裂抗拉强度均更高，0%、20%时高0.4MPa 左右，10%时高1.02MPa。0%、10%、20%铜尾矿掺量下，线性预测的抗折强度均更低，0%、20%时低1.6MPa 左右，10%时低2.39MPa。

线性预测结果与实验结果结果相比，0%、10%、20%铜尾矿掺量下，线性预测的劈裂抗拉强度与实验结果接近，均主要集中在4.4MPa 左右，预测精度较数值模拟更高。0%、10%、20%铜尾矿掺量下，线性预测的抗折强度均更低，0%时低0.81MPa 左右，10%时低1.13MPa，20%时低1.02MPa，偏差与数值模拟结果接近。