基于模糊纯追踪模型的最优预瞄研究

杨旭升

摘 要：预瞄距离对于纯追踪模型的影响至关重要，面对线性预瞄距离和非线性预瞄距离两种常见的预瞄距离选择，本文通过将车辆速度、道路曲率、横向偏差、航向偏差作为模糊控制器的输入，得到预瞄距离系数K，代入两种预瞄距离函数，探究在纯追踪模型的追踪效果。通过模拟两种预瞄距离在直线路段、曲线路段的追踪效果，得到非线性预瞄在两种路段追踪效果更加优越，符合人类驾驶员的驾驶行为。

关键词：模糊纯追踪 线性预瞄 非线性预瞄 横向控制

1 引言

新能源汽车产业的蓬勃发展推动了自动驾驶概念进入大众视野，从矿区、港口的特种智能汽车，到物流园区的无人分拣、配送车，在这其中，车辆运动控制是车辆安全平稳运行的最终保障。自动驾驶的控制系统可分为对汽车转向机构的横向控制，使车辆跟随期望轨迹行驶，以及对车辆制动、加减速的纵向控制。智能汽车的路径跟踪根据使用传感器的类型可分为预瞄式和非预瞄式[1]。非预瞄式横向控制应用于车路协同式车辆，即根据路测的智能基础设施获取车辆当前位置与期望路径的位置关系，控制车辆沿着期望路径行驶[2]。预瞄式即模仿人类驾驶员在道路行驶时，根据车辆当前时刻速度、位置信息和期望路径间的偏差，选择一个合适的预瞄距离计算方向盘或车辆前轮转向角度，达到预定轨迹。过于远的预瞄距离可能会使车辆提前对后续路段做出反应，轨迹跟踪效果偏离预期，过于近的预瞄距离可能会让车辆跟踪出现振荡[3]，因此预瞄距离的选取对车辆跟踪效果至关重要。

彭之川根据车速和道路类型选取不同的线性关系描述预瞄距离，使直道相较于弯道有更远的预瞄距离[4]，刘凯考虑预瞄距离与车速的关系，提出了预瞄距离与车速呈二次非线性关系，更为贴合人类驾驶员在高速情况下观察的实际情形[5]。郭壁玺将车辆横向偏差和航向偏差作为模糊控制的输入，计算得到不同情况下的车速增益[6]，张华强采用PSO算法自适应的计算预瞄距离，提升了车辆直线行驶时的精度[7]。但是，以上研究在探究预瞄距离对控制精度的影响时仅仅考虑车速、道路类型、横向偏差等单个因素，为此本文在综合考虑车速、道路环境、横向偏差、航向偏差等影响因素的基础上，使用模糊纯追踪模型探究线性预瞄距离、非线性预瞄距离对控制精度的影响。

2 理论模型

汽车运动学是从几何学的角度研究物体的运动规律，包括物体在空间的位置、速度等随时间而产生的变化，常见的运动学模型有以后轴为原点的车辆运动学模型、以质心为中心的车辆运动学模型、前轮驱动的车辆运动学模型等，本文采用以后轴为原点的车辆运动学模型。

2.1 二自由度汽车运动学模型

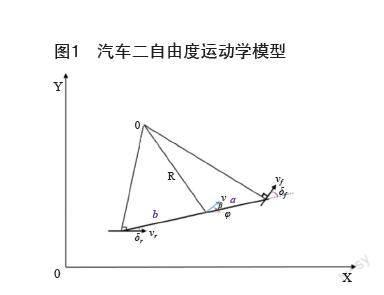
二自由度汽车运动学模型忽略了悬架的作用，将整车简化为两轮，认为轮胎侧偏特性为线性，忽略侧向力的作用，车辆不会进行俯仰及翻滚运动，始终在水平面运动，将汽车简化为线性二自由度模型可表示为图1所示。

根据几何关系和速度关系推导可得出：

其中XOY为大地坐标系，φ为横摆角，即车辆轴线与X轴方向夹角，β为质心偏侧角，即质心速度与车辆轴线的夹角，R为车辆转向半径，O为车辆瞬时转向中心，v为车辆的质心速度。在三角形中由正弦定理：

其中a，b分别为质心到前后轴的距离，由于车辆重量会影响质心位置，导致a，b长度改变，引入轴距L可得：

其中δf为前轮转角，δr为后轮转角。在低速状态下，认为车不会发生测向滑动，由vy≈0，可得。一般后轮不转向，即δr≈0，则有：

2.2 纯追踪模型

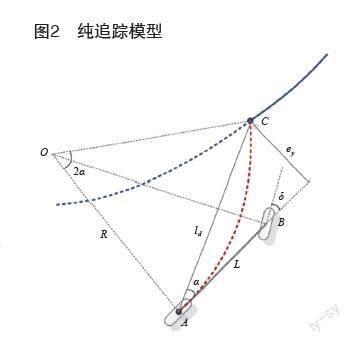
纯追踪算法通过将车辆从当前位置到目标位置间画一条圆弧，使车辆遵循一条经过目标点的圆弧行驶，在低速情况下可将车辆简化为两轮自行车模型，可将其简化为图2所示[9]。其中XOY表示大地坐标系，xoy表示车辆坐标系，L为车辆轴距，ld为车辆后轴到预瞄点的距离，ey为车辆距离预瞄点的横向距离，α为预瞄距离ld与车身轴线所处夹角，R为车辆转向半径。

在三角形OAC中由正弦定理：

可以得到：

由式（4）车辆的运动学方程有：

代入上式可得：

3 模糊控制器设计

将式（8）进一步处理可知，预瞄距离对车辆前轮转角的影响更大，其选取的结果直接影响车辆对规划轨迹的追踪效果，一种最常见的调整预瞄距离的方法就是将其表示成车辆纵向速度的线形函数，即

（9）

其中t表示预瞄时间，Lfmin表示最小预瞄距离，K为预瞄距离系数。

刘凯提出了一个车速的非线型函数[10]：

其中第一项表示车辆制动距离，，amax代表车辆最大制动加速度，第二项表示车辆碰到异常情况进行反应的车辆行驶距离，C表示车辆最小转弯半径。

为了得到参数K，按照人类驾驶员的驾駛经验，设定以下的预瞄距离规则：（1）速度越大，预瞄距离越远；（2）曲率越大，预瞄距离越近；（3）横向偏差越大，预瞄距离越近；（4）航向偏差越大，预瞄距离越近。

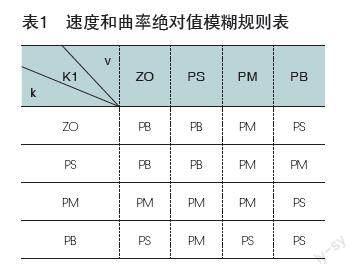
根据这个经验规则，我们选取速度、当前道路曲率、横向偏差、航向偏差作为模糊控制器的输入，输出为系数K，将计算的参数K代入两种预瞄距离，探究其优越性。表1、表2为计算预瞄距离系数K的模糊规则表，对经过模糊控制输出的系数K1、K2赋权重得到最后系数K。其中表1将速度v和曲率绝对值k作为模糊控制器的输入，输出为系数K1，表2将横向偏差?E、航向偏差?Yaw作为模糊控制器的输入，输出为系数K2。最终系数K由公式K=αk1+βK2（α+β=1）得到。

将速度v和曲率k的绝对值划分为4个模糊集合，横向偏差?E、航向偏差?Yaw划分为7个模糊集合，模糊集合的划分可以均匀划分也可不均匀划分，本文模糊集合的划分按不均匀划分。

4 仿真与分析

为了模拟真实环境中可能出现的道路情况，将仿真道路分为直线与曲线路段，其中直线段为一次函数型直线，曲线段为正弦函数型曲线，使用Matlab搭建模型，对式（9）线性预瞄时间t取2.5，Lfmin取1，得到线性预瞄距离函数，对式（10）非线性预瞄距离函数amax取3，B取0.2，C取1.5得到，车辆轴距L=0.9。

4.1 直线路段追踪效果

直线段函数表达式为y=4x+0.4，x∈[0，10]，车辆初始条件[x（0），y（0），yaw（0），v（0）]=[0，-0.5，-0.5，0]，直线路段的追踪如图3所示，追踪误差如表3所示。

在车辆初始条件偏离规划轨迹初始点的场景下，非线性预瞄相较于线性预瞄更快贴合规划轨迹，比线性预瞄提前3米将误差趋于稳定，而线性预瞄在0-2米内误差在持续增大，在实际应用场景中有较大的危险隐患。由表3可知，相较于线性预瞄，非线性预瞄各项数据均优于线性预瞄，跟踪误差更加平滑、波动更小，追踪效果更好。

4.2 曲线路段追踪效果

曲线段函数表达式为y=sin（x/2）*x/2，x∈[0，10]，车辆初始条件[x（0），y（0），yaw（0），v（0）]=[0，-0.5，-0.5，0]。曲线路段的追踪如图4所示，追踪误差如表4所示。

非线性预瞄在车辆初始条件偏离规划轨迹初始点的场景下，相较于线性预瞄追踪效果更佳，但因为预瞄距离变化过大引起前期出现短暂振荡，可对预瞄距离选取做相应限制得到改善。线性预瞄在曲线路段全程存在追踪偏差过大的问题，在实际场景的连续转弯路段追踪偏差会过大，同时由表4可知，非线性预瞄在追踪误差方面比线性预瞄变化幅度更小，收敛更快。

5 结语

本文综合考虑车辆速度、道路曲率、横向偏差、航向偏差等多种影响预瞄距离的因素，通过模糊控制器输出预瞄距离系数，结合纯追踪算法，得到车辆前轮转角。通过模拟线性预瞄函数和非线性预瞄函数在直线型路段、曲线型路段的追踪效果可知，非线性预瞄相比于线性预瞄误差收敛更加快、误差变化幅度更加小、追踪效果更加显著。但是当偏离规划轨迹较远时，非线性预瞄前期会有短暂的振荡现象，可通过限制预瞄距离梯度加以改善。由此可知，结合多种影响因子，使用非线性预瞄函数在模糊纯追踪算法中有着更加显著的追踪效果，非线性预瞄函数也更加符合人类驾驶员实际的驾驶行为。

参考文献：

[1]赵熙俊，陈慧岩.智能车辆路径跟踪横向控制方法的研究[J].汽车工程，2011，33（05）：382-387.

[2]高琳琳，戎辉，唐风敏，郭篷，何佳.自动驾驶汽车横向运动控制方法综述[J].汽车电器，2019，（09）：1-4.

[3]段建民，杨晨，石慧.基于Pure Pursuit算法的智能车路径跟踪[J].北京工业大学学报，2016，42（09）：1301-1306.

[4]彭之川，朱田，易慧斌.基于改进的Pure Pursuit智能客车轨迹跟踪算法研究[J].客车技术与研究，2019，41（05）：21-24.

[5]刘凯．无人驾驶车辆体系结构与定位导航技术研究 [D]．北京：北京理工大学，2010．

[6]郭璧玺，杜兴乐，陶小松.基于纯追踪模型的算法改进[J].汽车实用技术，2019，（15）：32-34.

[7]张华强，王国栋，吕云飞，秦昌礼，刘林，宫金良.基于改进纯追踪模型的农机路径跟踪算法研究[J].农业机械学报，2020，51（09）：18-25.

[8]忠厚老实的老王.三个坐标系与运动学方程.https：//www.bilibili.com/video/BV1gh411o7WJ.

[9]https：//img-blog.csdnimg.cn/20210418094129716.png？x-oss-process=image/watermark，type_ZmFuZ3poZW5naGVpdGk，shadow_10，text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L1Jvbm5pZV9IdQ==，size_16，color_FFFFFF，t_70.

[10]劉凯.无无人驾驶车辆体系结构与定位导航技术研究[D].北京：北京理工大学，2010.