二维稳态热传导CUDA 并行
2023-10-24王民
王 民
(烟台黄金职业学院,山东 烟台 265401)
0 引 言
有限差分法用于解决难以或无法分析解决的微分方程,其中包括拉普拉斯方程。求解拉普拉斯方程通常是为了找到平衡解,因此这是一个可以从物理问题中产生的方程。借助于有限差分实现二维拉普拉斯方程[1-3]在稳态热传导中的应用有助于解决其温度方面的问题。本文在基于有限差分的拉普拉斯方程程序编写基础之上,对其进行CUDA 并行化[4-5],提升数据计算的效率,从而得到更好的扩展性。
1 二维稳态热传导应用程序
1.1 二维稳态热传导理论
稳态热传导分析可以用来分析恒定中心热负荷对系统或部件的影响[6-7]。通常情况下,在进行临时热分析之前,要进行稳态热分析以确定初始温度分布。稳态热分析可用于分析温度等参数,这些参数是由恒定热负荷引起的,通过有限元素的计算,将连续的传热问题离散化为一系列离散的代数方程组,然后利用计算机进行求解。
1.2 有限差分的拉普拉斯
1.2.1 有限差分
有限差分法是一种数值方法,用于解决偏微分方程和积分方程。在有限差分法中,微分方程中的导数是用有限差分公式近似计算的[8-10],可以将[a,b]的区间划分为n个长度为h的相等子区间,如图1 所示。
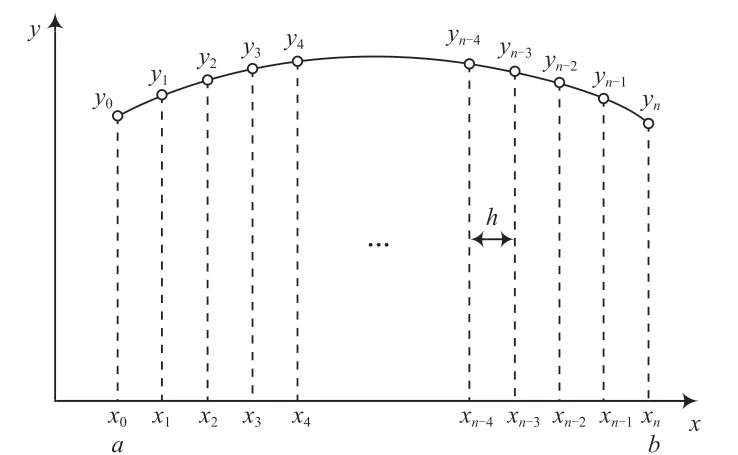
图1 有限差分法的区间划分
有限差分法基本上是一种近似导数的数值方法,所以先要分析如何取导数。一个函数f(x)的导数的定义如下:
通常情况下,在有限差分方法中使用中心差分公式,因为它们能产生更好的精度。微分方程只在网格点上执行,而第一和第二导数分别为:
这些有限差分表达式被用来取代微分方程中y的导数,如果微分方程是线性的,就会产生一个n+1 的线性代数方程系统。如果微分方程是非线性的,代数方程也将是非线性的。
在数值计算过程中,将解决方案区域划分为不同的网格,最终网格点用于替换不同网格中的连续解决方案区域。将要求解的流动变量存储在每个网格点,并用相应的微分商替换偏微分方程的微分元素,从而将偏微分方程转换为代数微分方程,获得离散点处具有有限未知变量的微分方程。通过求解微分方程,获得了网格点处流动变量的数值解。
1.2.2 二维的拉普拉斯方程
拉普拉斯方程是一个二阶偏微分方程,出现在许多科学和工程领域,如电力、流体流动和稳定热传导等。在一个领域中解决该方程,需要指定某些条件,即未知函数在域的边界必须满足的条件。在空间上二维拉普拉斯方程满足如下等式:
对x、y方向进行有限差分,并基于4 点格式执行计算。考虑到一块薄板的顶部和底部是完全绝缘的,它的每个边缘都有对应的已知温度。因此,目标是找到稳态温度的分布。区域内部的温度取决于它周围的温度。我们可以将该区域划分为细网状的点h(i,j)。一个内部点的温度可以被看作是四个相邻点温度的平均值,如图2 所示。
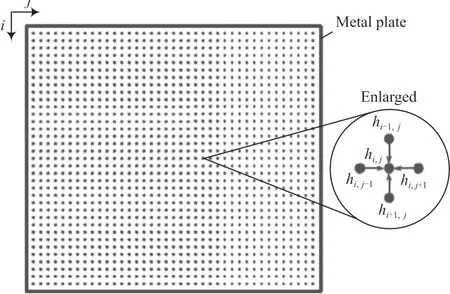
图2 四点差分区域划分
对于这种计算,采用与内部点相邻的点来描述边缘是很方便的。点h(i,j)的内部点是指0<i<n,0<j<n范围内的点,并且有(n-1)×(n-1)个点。边缘点是当i=0,i=n,j=0或j=n时,有对应于固定温度值的网格边缘点。因此,h(i,j)的全部范围是0 ≤x≤n,0 ≤y≤n,并且有(n+1)×(n+1)个点,可以通过迭代来计算每个点的温度方程。
1.2.3 串行和CUDA 并行化设计
(1)串行程序算法
假设每个点的温度被保存在一个数组h[i][j]中,边界点h[0][x]、h[x][0]、h[n][x]、h[x][n](0 ≤x≤n)已经被初始化为边缘温度。串行核心代码如图3 所示。
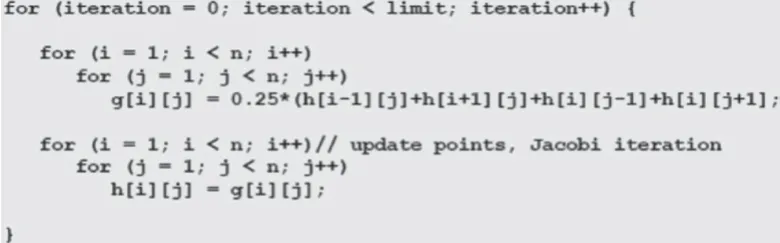
图3 串行核心代码
在计算过程中使用固定次数的迭代。请注意,图3 中第二个数组g[][]是用来保存从旧值中计算出的点的新值;数组h[][]被更新为g[][]中的新值;乘以0.25 而不是除以4 是为了使计算更有效率,因为乘法通常比除法更有效。提高顺序代码效率的方法可以延续到GPU 代码,并且在所有情况下都应该这样做。
将所要计算的薄板的两侧温度保持为20 ℃,其中一侧有较短的一段保持在100 ℃,如图4 所示。

图4 初始化薄板方法
(2)CUDA 程序算法
采用非共享方式实现对程序的并行。分别对x、y方向进行分块计算,每个块所启动的线程组数为x=(n+block.x-1)/block.x,y=(n+block.y-1)/block.y。
将核心计算部分封装到global 函数中,将每次的迭代计算结果拷贝回从设备重新参与计算工作。完成整个迭代后计算结果将被拷贝到主存中。
在从设备上执行计算,基于线程以及设备号获取每个数据块的坐标点。
2 正确性验证以及性能分析
2.1 正确性验证
对于程序正确性的验证,主要通过比较串行数据结果与并行数据结果来完成,程序上将计算结果保存到csv 文件中,借助于编写Python 脚本来读取两个文件的数值,对比每个数值点的值,当误差值在10 ~14 以内时,说明计算结果正确。通过对点的比较完成程序正确性验证。
2.2 性能分析
在测试中,本文选择的数组长度的计算规模分别是1 024、2 048,所使用的CUDA 方向上块的大小分别是(1,1)、(2,2)、(4,4)、(8,8)。迭代次数为固定值100。
通过测试记录串行时间以及并行时间,然后根据记录时间计算出程序的加速比S和并行效率E,通过这两个值分析程序的性能,如图5 所示。
从图5 中可以看出,在不同数据规模下程序的加速比和并行效率都得到改善。在相同规模下,随着分块数的增加,程序的加速比自增,且其并行效率也符合了小于1 的要求。在数据规模分别为1 024 和2 048 两种情况下,最大加速比值将是最小加速比值的N倍。
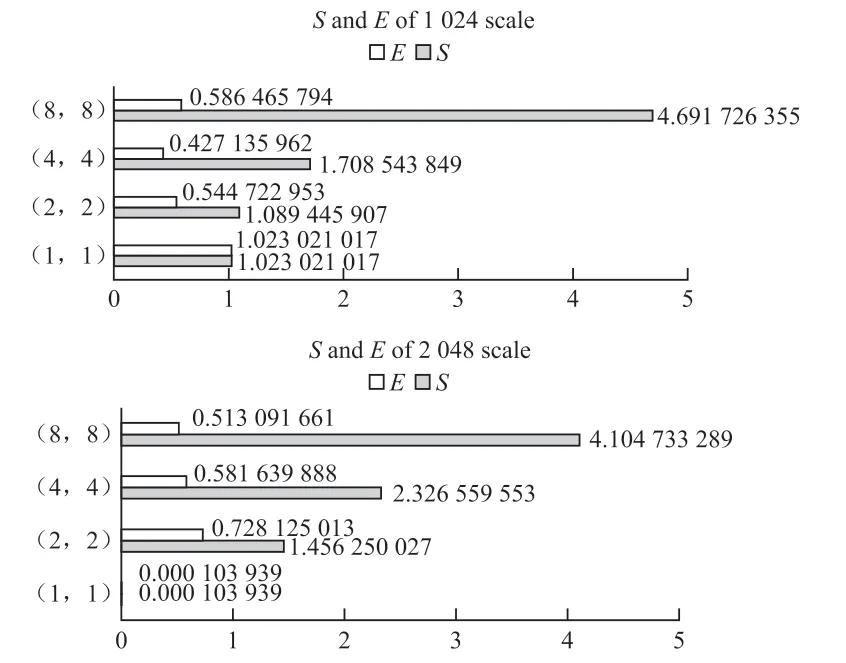
图5 加速比和并行效率
3 结 语
本文采用CUDA 实现了二维稳态热传导程序的并行化。分析测试数据得出,在执行并行化后,随着分块数的增加,其程序性能要比原来提升几倍。这对其实际应用有很大的帮助。
