基于区间orthopair模糊距离测度的ELECTRE Ⅲ决策方法

包恒嘉,周礼刚,肖 箭,石学成

(1.中国科学技术大学 管理学院, 合肥 230026;2.安徽大学 数学科学学院,合肥 230601;3.安徽大学 应用数学中心,合肥230601)

多属性群决策(MAGDM)是在一组评价指标的基础上,利用一定的决策方法选择出最优方案的决策过程,是当代决策科学研究的一个重要焦点.但是,受到事物本身的不确定性以及专家自身主观性的影响,在对问题进行评价的过程中会存在一定的模糊性.因此,如何通过对方案模糊信息的处理并排序以确定最优方案成为一个热门的研究课题.

为了解决人类在面对复杂问题提出的模糊评价结果,Zadeh[1]在1965年提出了模糊集(FS)的理论.众多学者在此基础上进行了深入研究,如Atanassov[2]提出了直觉模糊集(IFS)的概念,在区间[0,1]上定义了隶属度和非隶属度的概念;Yager[3]提出了毕达哥拉斯模糊集(PFS)的概念,来描述隶属度和非隶属度的平方和小于1的情况,例如0.6+0.7>1,但是在毕达哥拉斯模糊集下0.62+0.72<1;对于更复杂的现实问题,Yager[4]又提出了q-rung orthopair模糊集的概念来描述隶属度和非隶属度的q次方和小于1的情况.随后,Ju等[5]将q-rung orthopair模糊集推广到区间形式,从而将隶属度与非隶属度引申到区间形式.

在多属性决策过程中,经常会用到一些经典的决策方法,例如VIKOR方法[6],TOPSIS方法[7],ELECTRE方法[8]等.Benayoun等[9]在1966年提出了ELECTRE方法,该方法基于超越关系以及一致性和不一致性的概念[10],通过使用一致性指数和不一致性指数分析对方案进行排序[11].在ELECTRE方法提出不久后,许多学者对其进行研究改进和推广,于是出了对ELECTRE Ⅱ、ELECTRE Ⅲ、ELECTRE Ⅳ、ELECTRE IS和ELECTRE TRI等[12-15]多种方法.

目前来说,ELECTRE Ⅲ因其使用伪准则以及能处理不精确的初始数据等优点,被广泛应用于区间直觉模糊集[16]、区间毕达哥拉斯模糊集[17]中.考虑将ELECTRE Ⅲ与区间q-rung orthopair模糊集结合,提出q-rungorthopair ELECTRE Ⅲ方法,并利用Chebyshev距离测度、最大偏差法进行决策,最终结合证券投资的多属性决策案例分析方法的有效性和准确性.

1 预备知识

定义1[18]设X为一论域,则X上的一个q-rung orthopair模糊集(q-ROFS)可定义为:

G={x,uG(x),vG(x)|x∈X},

(1)

其中:函数uG(x)∶x→[0,1],vG(x)∶x→[0,1]分别为元素x属于X的隶属度和非隶属度,并满足约束条件0<(uG(x))q+(vG(x))q≤1,(q≥1),则q-ROFS的犹豫度可表示为:

πG(x)=(1-(uG(x))q+(vG(x))q)1/q,

(2)

其中:πG(x)∈[0,1].

特别地,当q=1时,G为直觉模糊集;当q=2时,G为毕达哥拉斯模糊集.同时,为了方便起见,称(uG(x),vG(x))为q-rung orthopair模糊数(q-ROFN),表示为(uG,vG).

定义2[19]设X为一论域,则X上的一个区间q-rung orthopair模糊集(q-RIVOFS)可定义为:

(3)

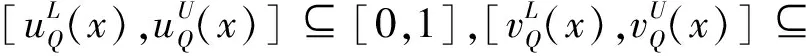
(4)

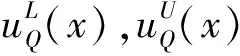
(5)

1)加法运算

2)乘法运算

3)数乘运算

4)幂运算

(6)

(7)

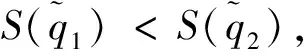
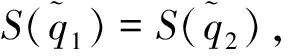
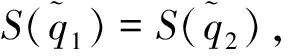
2 一种新的区间q-rung orthopair模糊距离测度

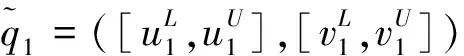
(8)

证明：1)、2)显然成立,下证3).

定理证毕.

3 基于新的区间q-rung orthopair模糊距离测度的ELECTRE Ⅲ方法

(9)

步骤 3:求解属性权重向量Ω=(ω1,ω2,…,ωn)T,可构建如下偏差最大化模型:

(10)

利用拉格朗日乘数法可求得:

(11)

标准化即可得到:

(12)

步骤4:利用式(13)构造属性cj下,方案ai与al之间的和谐系数:

(13)

步骤5:根据式(14)计算方案ai与al的一致优先度:

(14)

步骤6:利用式(15)计算属性cj下,方案ai与al之间的不和谐系数:

(15)

步骤7:利用式(16)计算方案ai与al的超序度:

(16)

步骤8:利用式(17)计算方案ai的一致可信度:

(17)

利用式(18)计算方案ai的不一致可信度:

(18)

利用式(18)计算方案ai的净可信度:

Φ(ai)=Φ+(ai)-Φ-(ai),i=1,2,…,n.

(19)

净可信度Φ(ai)反映了ai排序的级别优先性,即Φ(ai)越大,ai的排序越靠前.

4 案例分析

在经济空前繁荣的大背景下,证券投资是热门话题之一.三位基金分析人(dk,k=1,2,3)针对5项基金购买属性指标:基金收益能力(c1)、风险控制能力(c2)、业绩持续能力(c3)、经理择股能力(c4)以及经理择时能力(c5)进行综合评估,运用区间q-rung orthopair模糊数表示.

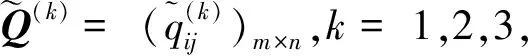
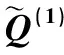
表1 专家d1的区间q-rung orthopair模糊评价矩阵

表2 专家d2的区间q-rung orthopair模糊评价矩阵Table 2 Interval q-rung orthopair fuzzy evaluation matrix of expert d2

表3 专家d3的区间q-rung orthopair模糊评价矩阵Table 3 Interval q-rung orthopair fuzzy evaluation matrix of expert d3

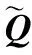
表4 区间q-rung orthopair模糊评价矩阵Table 4 Interval q-rung orthopair fuzzy evaluation matrix

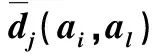
表5 不和谐系数Table 5 Discordance index

步骤 3:根据式(12)计算每个方案的属性权重向量Ω,得到

Ω=(0.204 5,0.149 9,0.301 2,0.202 4,0.142 0)T.

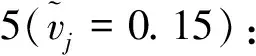
步骤6:由式(16)计算方案ai与al的超序度,得到如下超序度矩阵:

步骤7:根据式(19)计算各方案的净可信度,得到:

Φ(a1)=0.718 8,Φ(a2)=-3.520 0,
Φ(a3)=0.578 9,Φ(a4)=-0.162 9,
Φ(a5)=0.2385 2.

显然,Φ(a5)≻Φ(a1)≻Φ(a3)≻Φ(a4)≻Φ(a2),故a5≻a1≻a3≻a4≻a2,即最优方案为方案a5,说明购买第5种证券投资基金收益最大.

为了考察不同的q值变化对决策方案的影响,分别取q=1,2,…,10,净可信度图像如图1所示.

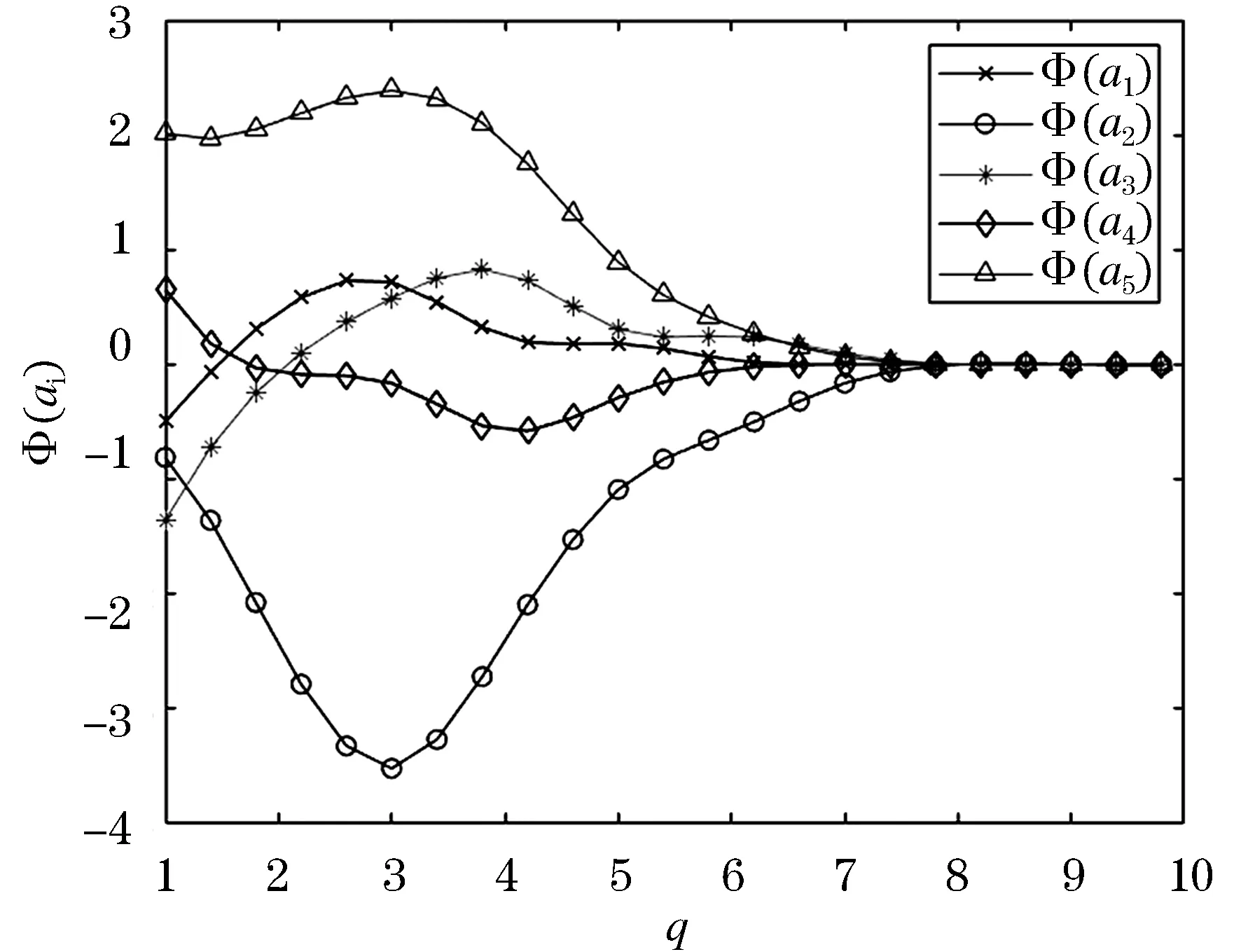
图1 净可信度Φ(ai)随q值变化图Figure 1 Change of net credibility Φ(ai) with value q

从图1可以看出随着q值变化对决策方案的影响,随着参数q的取值变化,决策结果的方案排序有所变化,但最优方案都是a5,最劣方案都是a2,其他方案的排序略有波动,与文献[7]中的排序结果基本相同,说明提出的基于新的区间q-rung orthopair模糊距离测度的ELECTRE Ⅲ方法的有效性和实用性.

对于多属性群决策问题,除了考虑客观的属性指标对决策结果的影响,还要考虑到专家对阈值的考量.新的区间q-rung orthopair模糊的ELECTRE Ⅲ方法使用伪准则,使得其具有能处理不精确初始数据能力.文献[16]和[17]分别提出了基于区间直觉与区间Pythagorean模糊的ELECTRE Ⅲ方法,相比较而言,提出的方法能解决实际问题的范围更广泛,可根据不同情况调节参数q的大小.

5 结 语

本文提出了一种基于区间q-rung orthopair模糊的Chebyshev距离测度、最大偏差法以及ELECTRE Ⅲ的多属性群决策方法.首先提出了基于区间q-rung orthopair模糊的Chebyshev距离测度,并讨论其性质;在其基础上提出求属性权重的最大偏差模型,在权重未知的情况下求解属性权重;最后利用区间q-rung orthopair模糊的ELECTRE Ⅲ方法,解决了证券投资方案选择问题.通过与过去决策方法的对比,验证新方法具有有效性和实用性.