CO2在微通道内高速流动特性的研究

王亚宾,翁建华,崔晓钰

(1.上海电力大学 能源与机械工程学院,上海 200090;2.上海理工大学 能源与动力工程学院,上海 200093)

1 引言

微通道的新型冷却技术正在不断发展。微系统技术通过对电子器件的微型化、集成化的方式实现了在有限空间内完成一系列复杂繁琐的设备运行程序,如芯片级集成微系统等。从电子器件发展历程来看,随着电子器件的不断微型化,散热问题已成为电子器件研究制造环节所要解决的必要问题。设备尺寸减小以及功率的增加,当前一些用于电子设备的冷却装置已经不能满足人们的需求,如何在系统整体功能不变的前提下,使得存储空间更小、散热更快是这个领域目前所要突破的关键[1]。

微型焦耳-汤姆孙效应制冷器因其具有结构简单、重量轻、价格低、制冷速度快等优势,被广泛应用于电子器件的冷却。考虑到焦汤效应制冷器的冷却能力小,She Hailong等[2]研究了一种具有平行微通道的多层印刷电路板J-T,以氩气为制冷气体,入口压力为8.02 MPa时的冷端温度可达155.9 K,总制冷量3.66 W,忽略轴向热传导时冷端温度可达154.7 K;S. P. Narayanan等[3]从制冷器设计的角度对实际微型制冷机热交换器的控制方程进行数值求解,设计出一种回热段采用曲折型设计的单层微通道制冷器来增强其换热能力。

此外,很多学者对微通道流动特性展开研究。J. C. Harley等[4]使用硅晶片刻蚀的微通道对氮气、氦气和氩气的流动进行了研究,所测得的摩擦因数与等温假设下一阶滑移边界条件局部完全发展段的理论预测结果非常一致;M. J. Kohl等[5]将入口压力分别为49.8、97.5和153 psig的空气经过用3个硅芯片组成的矩形微通道,测得的压力分布与数值预测吻合;C. Hong等[6]通过使用停滞压力、局部压力及质量流量获得氮气通过微通道时的局部马赫数、温度和摩擦因数,在范诺流假设的前提下局部范宁摩擦因子几乎与布拉休斯的相关性重合。还有一些学者表明微尺度管段计算方法与宏观管段计算不同。W. Peiyi等[7]使用氮气、氩气以及氦气分别测量了硅和玻璃微通道内气体流动时各管段截面的摩擦因数,结果表明,与宏观管段相比微通道内的摩擦因数要高出10%～30%;R. Raju等[8]以N2和He为工作流体建立流体力学模型,研究了微通道内两种不同情况的高速可压缩气体的流动传热特性,其结果与Monte Carlo模拟的结果存在一些明显的差异;G. L. Morini等[9]研究相对粗糙度、可压缩性和通道长径比对转捩雷诺数的影响时发现在没计算失误的情况下得到的临界雷诺数与期望值不符。

上述学者研究的差异表明,对微通道内流体的流动特性研究是必要的。环境友好型工质CO2与制冷剂R134a和R1234yf相比,具有无毒、化学性质稳定、蒸发潜热大、单位容积制冷量高等特点[10]。此外,CO2与微通道的结合提供了重量轻、压实度高和传热系数高的CO2热交换器[11]。以CO2为工质,建立矩形微通道流动模型,在绝热流动与非绝热流动的假设下对微通道的流动特性进行研究。

2 流动模型的确定

在微尺度流动中,当微通道的几何尺寸远大于流体分子的平均自由程时,常规尺度下的模型和方程仍然可以使用,但当流体流动的微通道的几何尺寸很小时,不同的影响因素对其内部流体流动影响发生改变,从而导致在微通道中的流动状况产生变化。在微尺度下的流动,还存在壁面的滑移效应、稀薄效应以及可压缩性的影响。引入一个无量纲参数努森数(Kn)来划分微尺度流动与常规尺度流动[12]。Kn数定义为分子平均自由程和流动特征尺寸之比,可由式1计算:

(1)

式中,λ是气体分子平均自由程,单位为m;d是水力直径,单位为m。

气体分子平均自由程λ可由式2计算:

(2)

式中,μ是线性系数;R是为气体常数,单位为J/(kg·K);T是流体局部温度,单位为K;ρ是流体局部密度,单位为kg/m3。

根据Kn数的大小将气体划分为4个流动区域,对应的流动模型及流动尺度见表1。

表1 不同Kn数下流动尺度及流动模型

当Kn数小于10-3时,气体分子之间的碰撞频率远高于气体分子与壁面原子之间的碰撞频率。经计算,研究的5种工况下,CO2气体在微通道凹槽不同位置处的Kn数均远小于10-3,因此流动区域可视为连续介质区,N-S方程和Fourier’s Law均适用,气体与壁面交界处不存在速度滑移。

3 理论计算及数据分析

3.1 理论计算方法

对微通道进行分段计算,将长为L的微通道均匀分段,每一小段的微通道长度为l=L/n,n为段数。给定入口压力和温度时根据热物性表可以查得入口截面处CO2的密度ρ0、比焓h0、气体运动粘度v0、当地音速c0以及比热比γ等。

CO2通过矩形微通道的速度可由式3计算得出:

(3)

式中,u是气流速度,单位为m/s;s是质量流量,单位为g/s;ρ是密度,单位为kg/m3;A是截面面积,单位为m2。

马赫数Ma由式4计算得出:

(4)

式中,γ是比热比;R是气体常数,单位为J/(kg·K);T是温度,单位为K。

当Re<105时,沿程阻力系数f′可选用布拉休斯公式f′=0.316 4Re-0.25来计算,但是随着Ma的增大,等温流假设下的得到的摩擦因数f越来越偏离布拉休斯的表述,于是要引入对摩擦因数的修正,根据C. Hong等[13]的研究,修正后的摩擦因数fd可由式5计算得出:

(5)

假设第1段管段出口密度为ρ1,通过式6计算管段压降:

(6)

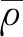
第1段出口气体压力p1可由式7计算:

p1=p0-Δp1·10-6

(7)

式中,p0是管段进口压力,单位为MPa;p1是管段出口压力,单位为MPa。

第1段出口比焓可由式8计算:

(8)

式中,h0是入口CO2比焓,单位为kJ/kg;h1是出口CO2比焓,单位为kJ/kg;u0是入口速度,单位为m/s;u1是出口速度,单位为m/s。

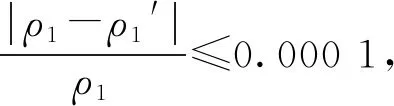
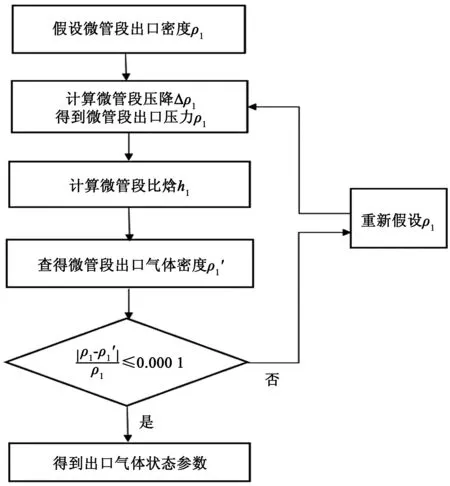
图1 计算流程框架

根据上述计算得出第1段出口参数,计算第2段、第3段直至第n段的出口参数,得到最终微通道出口端的温度与压力,进而分析各微管段流动的影响因素,迭代过程由MATLAB完成。

对于换热量已知时的非绝热壁流动,从能量平衡角度分析流动过程, 整个微通道视为一个整体取微管段进行分析。水平管道不考虑位能损失,即g(z2-z1)=0。根据式5和式8,绝热壁q=0时,截面处的摩擦因数和比焓均是截面流速的函数。对于非绝热壁面,外界对系统做功使得气体焓值增加或降低,当槽道分段很多时,出口焓值就可近似由式9计算得出。假设凹槽受热均匀,相对于绝热壁流动,每个微管段焓值改变,其他流动参数随之改变,通过迭代计算可得到换热量已知时的非绝热流动的出口参数。

(9)

式中,q是换热量,单位为kJ/kg。

3.2 计算结果与分析

3.2.1 绝热流动的计算结果与分析

以C. Hong等的研究为例验证上述方法的准确性,其使用通过30%的KOH溶液刻蚀硅片与玻璃板结合的微通道,对氮气在微通道的流动特性进行了研究,所采用的一种微通道长26.9 mm、宽1 020 μm、高112.7 μm,水力直径为203 μm。取入口压力Pin分别为0.19、0.56和1.01 MPa,入口处马赫数Ma分别为0.27、0.32和0.34,入口温度t分别为292.5、289和288 K。

将微通道划分为2 690段,用该理论计算方法计算得到的Ma如图2所示。将其通过实验测得的数据与图2进行对比,从图2中可以看出,数据与实验得到的数据十分吻合。

图2 Ma沿流动方向的变化

调整微通道长度后对压力和温度进行计算,压力与温度的变化如图3和图4所示。在距入口端23 mm处,进口压力为0.19 MPa的N2工况压力降低至0.116 MPa,温度从292.5 K降至285.66 K,降低了6.84 K;进口压力为0.56 MPa的N2工况压力降低至0.318 4 MPa,温度从289 K降至277.41 K,降低了11.59 K;进口压力为1.01 MPa的N2工况压力降低至0.573 2 MPa,温度从286 K降至272.84 K,降低了13.16 K,所得数据与试验结果十分吻合。

图3 压力沿流动方向的变化

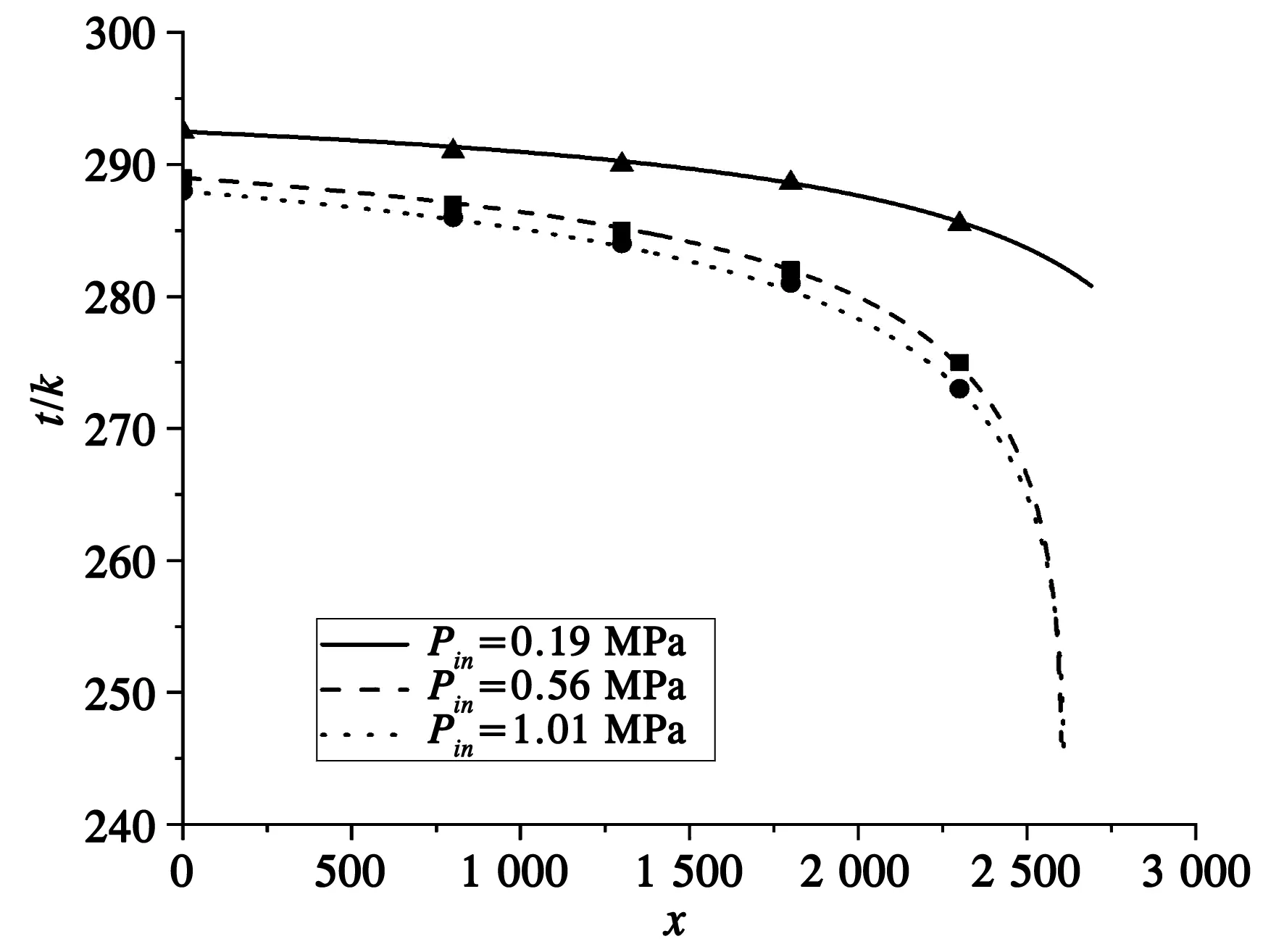
图4 温度沿流动方向的变化

对CO2在矩形微通道内的流动特性进行计算,槽道长L=40 mm,宽w=0.7 mm,高H=0.7 mm,水力直径D=0.7 mm,入口压力分别为0.3～0.7 MPa,质量流量s=0.5 g/s,温度Tm=14 ℃,分析不同入口压力对CO2流动参数的影响。

通过改变入口压力,保持温度及质量流量不变,5种状态的马赫数变化如图5所示。可以看出,在进口低压时相应的马赫数反而越大,这是由于温度不变,压力降低,流体密度较低,从而质量流量恒定时流速较高,相应的入口处马赫数越大。沿流动方向的摩擦因数越来越大,到达某一位置后流动达到临界状态发生壅塞。对于每个给定入口状态,马赫数都有确定的极限长度Lcr。马赫数沿流动方向逐渐增加。槽道入口压力和温度恒定,质量流量相同,入口压力越低,马赫数在流动过程中增加越快。

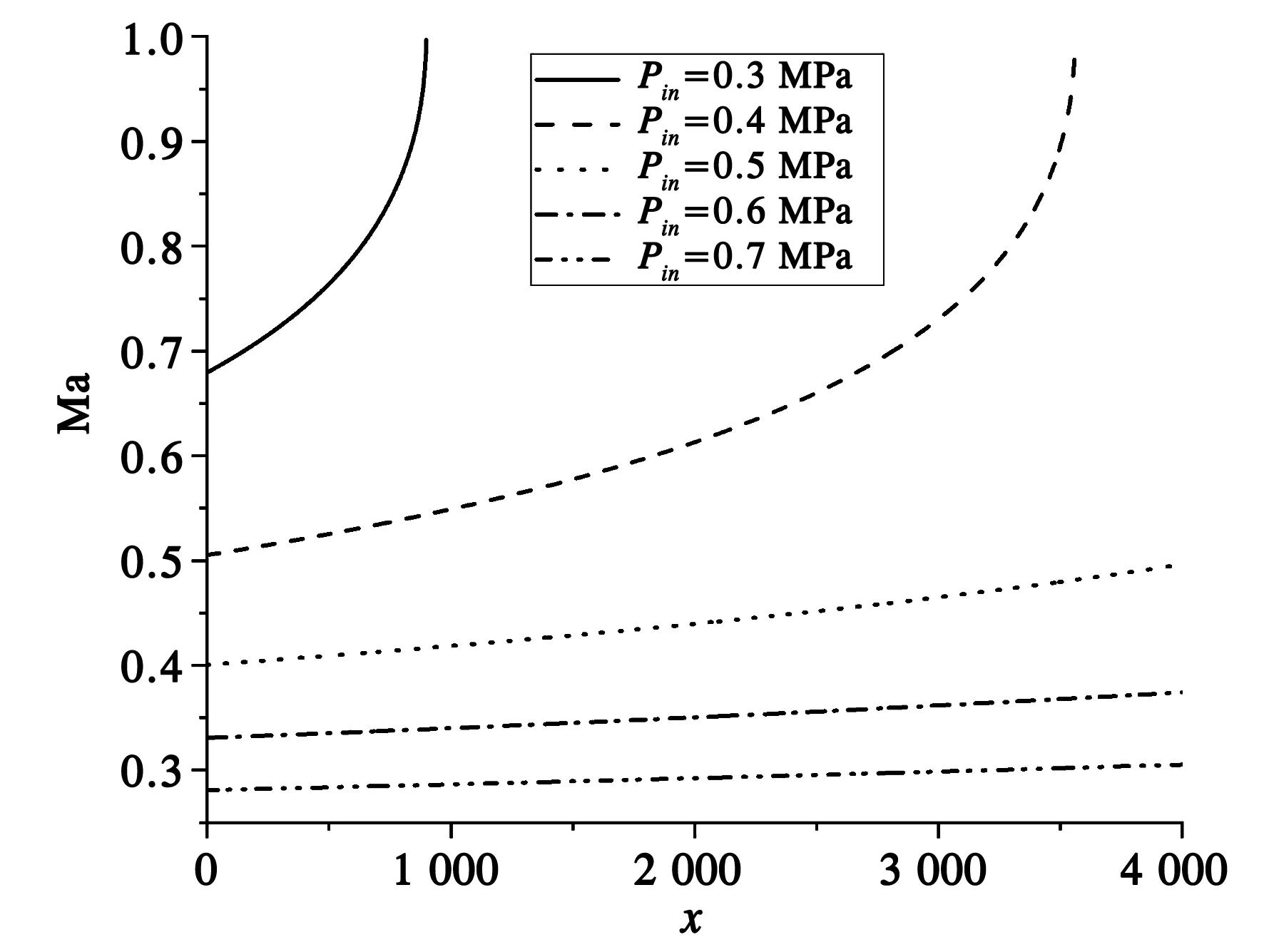
图5 五种状态的Ma沿流动方向的变化

管段压力沿流动方向的变化曲线如图6所示。沿流动方向压力不断降低。入口压力较低时的气流速度较高,由式5可得,此时摩擦力相对于入口压力较高的管段更大,使得在相同管段长度下的压降更大,同时更容易速度达到临界,管段发生壅塞。

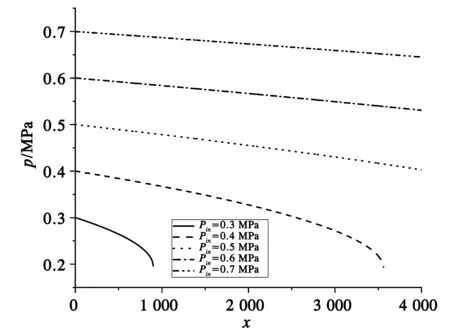
图6 压力沿流动方向的变化

温度沿流动方向的变化曲线如图7所示。气体温度沿通道长度逐渐降低。在槽道未发生壅塞时,入口压力为0.3和0.4 MPa的冷端温度分别可达-9.91和-16.45 ℃,管段长度相同时,相对于另外3种工况制冷效果更为显著。经计算,适当增加管段长度,使得入口压力为0.5、0.6和0.7 MPa的流动接近临界状态,这时的冷端温度分别可达-19.7、-22.96和-25.82 ℃,此时对应的极限长度分别为0.078、0.135和0.207 m。可见高压工况的冷端温度更低,但需要更长的管段去实现。低压工况需要考虑管段壅塞,在管段长度一定时,低压工况的温降变化更为显著。

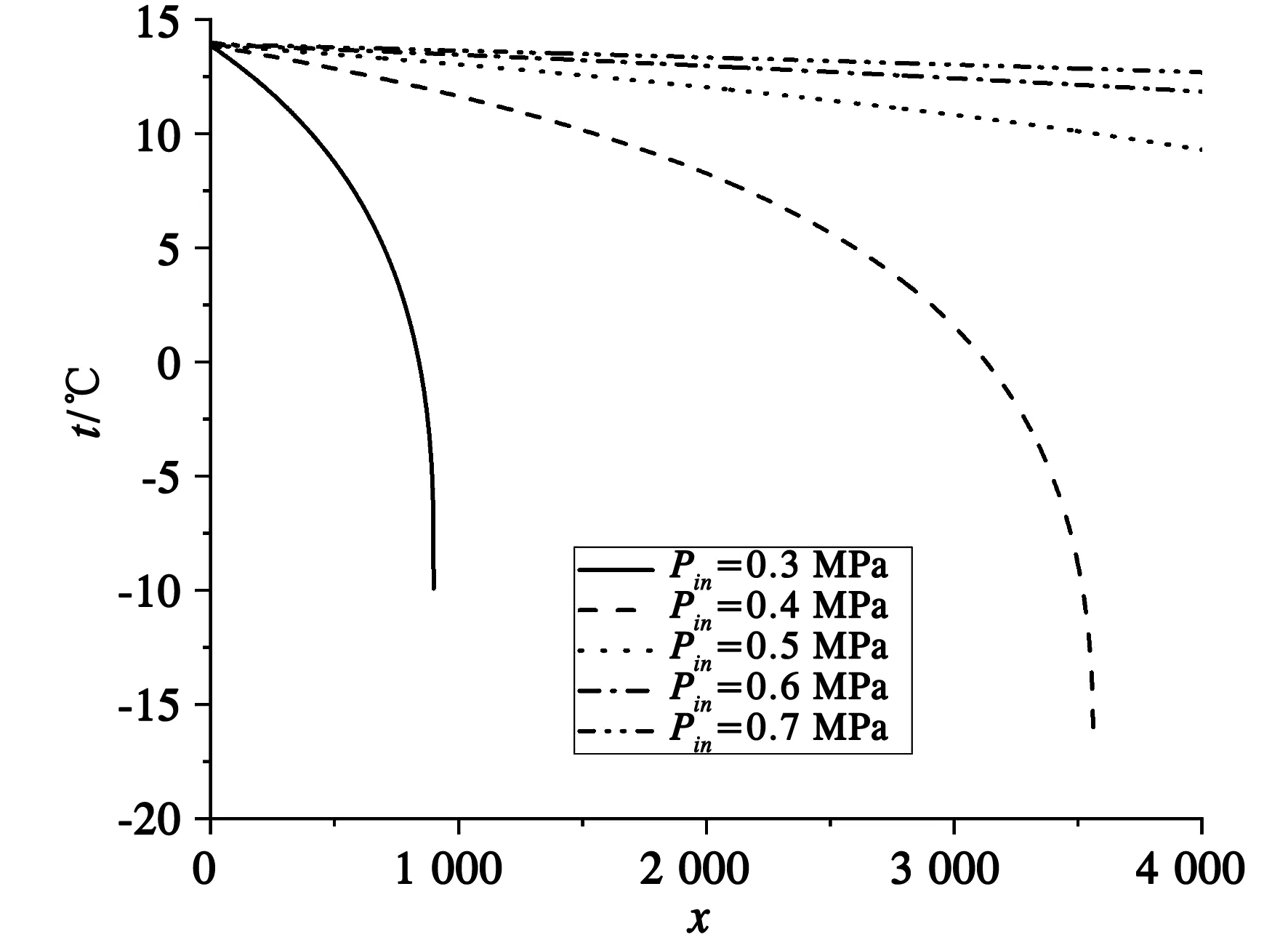
图7 温度沿流动方向的变化

微通道高度H分别为0.7、0.35和0.175 mm时,质量流量调整为s=0.15 g/s,其他参数不变。此时不同凹槽高度时温度的变化曲线如图8所示。凹槽出口冷端温度分别为13.85、13.39和-5.86 ℃,可以看到对于尺寸越小的微通道凹槽,温降变化越大,相对于尺寸较大的凹槽,制冷效果更为显著。

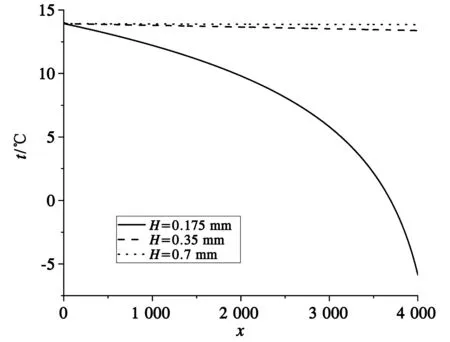
图8 不同槽道高度时温度的变化

3.2.2 非绝热流动的计算结果与分析

非绝热壁以CO2入口压力0.5 MPa为例,槽道长L=40 mm,宽w=0.7 mm,高H=0.7 mm,水力直径D=0.7 mm,质量流量s=0.5 g/s,温度Tm=14 ℃。相对于绝热壁工况,出口参数见表2。可以看出,外界对系统输入热量为正时,出口压力降低,比焓增加,密度降低,流速增加,马赫数增加;反之,输入热量为负时,出口压力升高,比焓降低,密度增加,流速降低,马赫数降低。

表2 不同壁面换热功率时的出口流动参数

如果以CO2气体进口压力为0.3和0.4 MPa的工况进行非绝热壁计算,槽道内流体达到临界状态时的位置有所变化。要使槽道受热全部作用于有效管段,就需要提前设计槽道长度,使得气体在不发生壅塞的前提下通过整个槽道。此时入口压力为0.3和0.4 MPa时的非绝热壁换热极限管长见表3。由表3可知,加热时极限长度减小,冷却时极限长度增加,换热条件下的极限管长长度随换热量而改变。

表3 不同壁面换热功率时的极限管长

4 结语

本文针对不同入口压力时的CO2气体高速通过矩形微通道的流动特性进行研究,使用迭代计算得到冷端温度,进而分析影响冷端温度的因素。根据热物性表,使用压力与比焓拟合流动参数并用实验数据验证了理论计算方法的合理性。然后对给定质量流量的工况进行分析,结果表明,入口低压时温降变化更为显著。微通道凹槽尺寸对冷端温度的影响也非常重要。在换热条件下的极限管段长度随换热量的不同而发生改变,在避免发生壅塞的前提下适当增加管段长度可以得到更低冷端温度。所得结论总结如下:1)理论计算结果与试验文献结果十分吻合,验证了理论计算方法的合理性;2)质量流量相同时,低压工况温降更大,但容易发生壅塞;3)槽道尺寸越小,温降变化越为显著;4)微通道内的高速流动,可以通过设计槽道尺寸、调节换热量的方式得到理想的冷端温度。