南昌市低影响开发设计降雨量的确定方法研究

2023-10-22张景嵘温鸿安刁川悦刘卫林刘丽娜金志农

水利规划与设计 2023年10期

张景嵘，温鸿安，刁川悦，刘卫林，李香，吴滨，刘丽娜，金志农

(南昌工程学院江西省水文水资源与水环境重点实验室，江西南昌 330099)

南昌市地处长江下游的鄱阳湖南岸平原内，属亚热带季风气候。境内河流水系湖泊众多，主要河流有赣江、抚河、锦江、潦河，是全国首批确定的25座防洪重点城市之一。近年来，随着城市化进展加快和全球气候变化，由暴雨引发的南昌城区局部内涝积水频繁发生，尤其是近几年来汛期“城市看海”几成常态，已严重威胁到人民的生命财产安全。据统计，1985—2007年南昌市气象灾害累计116次，其中由暴雨引发的城市内涝占33.62%[1]。因此，城市防洪防涝任务日益紧迫，城市水管理工作面临着巨大挑战。

针对近些年国内城市防洪排涝日趋严重问题，我国提出了海绵城市这一新型城市雨洪管理理念。2014年，《海绵城市建设技术指南——低影响开发雨水系统构建(试行)》(简称《指南》)开始实施，作为各城市海绵城市建设的依据和指南[2]。《指南》指出，低影响海绵城市开发建设目标一般可以通过径流总量控制来实现，并提供了低影响开发(LID)条件下预估降雨量的确定方法，即采用年径流总量调节率确定适当的设计降雨量[3]，表明年径流总量控制率与设计降雨量之间有一一对应关系[4]。《指南》中设计降雨量的确定方法是将30年以上的历史日降雨数据按照由小到大顺序排序后求出不同降雨时段的多年平均降雨量，从而确定标准控制率下对应的雨量值。由于降雨的年际变异性，采用这种多年平均的方法仅能体现降雨量的多年平均控制程度，其置信概率有待进一步确定[5]。此外，还有专家指出该方法未明确“年控制”的概念，多年平均的方法无法与我国雨水系统设计标准采用的重现期法一一对应[6-7]。

为此，笔者以南昌市30年以上的实测降雨资料为例，分析其在多年平均和年单样本两种方法下低影响开发设施的降雨量设计问题，并通过P-Ⅲ型频率曲线推求了年单样本方法下的设计降雨量，最后将两种方法得到的不同的标准控制率下的设计值与《指南》中的同标准设计值进行比较，以期为南昌市海绵城市建设控制指标的合理确定提供科学依据。

1 研究区概况及数据来源

南昌市位于江西省中部偏北，赣江、抚河尾闾，鄱阳湖南岸平原内，全市中部地形低，平坦开阔，西部及东南部较高，平原、山地、岗地、低丘相间分布。陆地总面积为5197.99km2，其中平原面积2649.72km2，岗地低丘面积2548.27km2；水域面积2204.37km2。南昌市属亚热带季风气候，雨水充沛。降水年内分布不均匀，多年平均降水1567.7～1654.7mm，4—6月降水约占全年的一半，7—9月降水量只占全年19%。境内河网密布，湖泊众多，水系发达，水域总面积2200km2，占国土总面积的29.7%。多年平均径流深为649.6mm，季节变化明显，最大径流一般出现在5、6月，约占全年的22%，最小径流在1月或12月，占全年2%。

《指南》中年径流总量控制率的计算主要是基于1983—2012年降水数据。考虑到《指南》是在2015年编制完成的，之后再也没有更新。因此，选择最新降水数据加入到年径流总量控制率和设计降雨量的计算中，将使结果变得更加准确和具备时效性[8]。参考南昌市地理位置的具体情况和数据采集的具体情况，本次计算采用南昌市1951—2019年逐日降雨量数据。上述数据可从中国气象数据网(http//data.cma.cn)获取。

2 设计降雨量确定的方法

2.1 多年平均设计方法

根据《指南》规定，多年平均法要求选取至少近30年日降雨资料(扣除小于等于2mm降雨事件的降雨量)，将日降雨量由小到大排序，统计小于某一降雨量的降雨总量在总降雨量中的比率，此比率(即年径流总量控制率)对应的降雨量即为设计降雨量[2，9]。具体计算公式如下：

(1)

式中，RV—年径流总量控制率；P设计—设计降雨量，mm；Pi—第i个日雨值；mm；N—总降雨天数；m—超出P设计的降雨天数。

2.2 年单样本设计方法

《指南》以年降雨总量控制率作为径流总量控制目标，并由多年全样本统一排序的方式确定标准控制率下对应的设计降雨量。然而研究表明基于多年平均样本的低影响开发设施的设计降雨考虑的是多年平均降雨水平，基于该设计值开发的设施是否能实现单年的降雨总量控制还存在理论争议[8-10]。而年单样本法能给出不同频率下的设计降雨量，以实现统计意义上的“年控制”，提高城市的降雨控制水平。因此，本文使用年单样本法计算不同控制率下的设计雨量，给出设计降雨实现降雨总量控制的机率，提高低影响开发设施对降雨的控制水平。

与《指南》中的多年平均法不同，年单样本法首先将每个统计年的日降雨量从小到大排序，然后确定当年满足控制要求(由总降雨量控制率确定)的降雨量值被认为是当年的唯一代表样本，最后结合选出的频率分析结果，计算出不同频率下设计降雨量。由于该方法选取的样本不是年最大值样本，而是对应满足总降雨控制率要求的年内分位数，因此，这种方法能够更好地对应“年控”的概念，反映了单年降水量的年均值[8，11]。

频率分析是年单样本方法中最为关键的步骤，一般能够借助拟合经验频数分布曲线来实现。常见的频率分布曲线有极值分布、皮尔逊Ⅲ型分布和对数正态分布等。考虑到我国最常用的是皮尔逊III型分布[12]，因此，本研究选用皮尔逊III型曲线进行频率分析。采用年单样本方法推求设计降雨量，具体步骤如下：

(1)将日降雨数据按顺序进行整理。剔除降雪等非降雨数据和异常数据，并扣除累计小于或等于2mm的日降雨数据。

(2)基于降雨数据，以年为基本单位，根据《指南》中南昌市所处的降雨控制率区域，选择70%、75%、80%、85%控制率确定出对应控制率下的雨量值，得到逐年单样本雨量系列值，如图1所示。

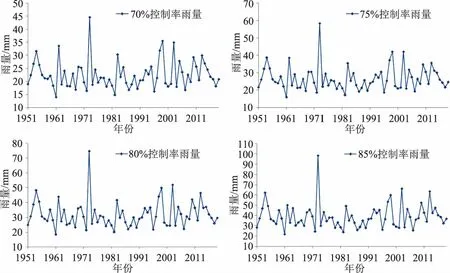
图1 控制率雨量

(3)对得到的年单样本降雨序列进行降序排序，计算经验频数。

(4)采用P-Ⅲ型分布曲线进行频率分析，计算均值(Ex)、变差系数(Cv)和偏态系数(Cs)等统计量。

(5)结合不同的设计频率p，计算标准控制率下的设计降雨量P设计，具体公式如下：

P设计=Ex·(Cv·φp+1)

(2)

式中，φp—设计频率p下的离均系数[13]。

3 结果与分析

3.1 多年平均法下的设计降雨量

《指南》中依据1983—2012年降雨资料给出了南昌市60%、70%、75%、80%、85%年径流总量控制率下的设计降雨量分别为16.7、22.8、26.8、32.0、38.9mm。本文根据南昌市1951—2019年的日降雨数据，根据《指南》中设计降雨量的计算方法，对南昌市设计降雨量进行了重新计算，给出了设计降雨量与年径流总控制率的关系。计算的控制率见表1。>32.0、38.9mm。本文根据南昌市1951—2019年的日降雨数据，根据《指南》中设计降雨量的计算方法，对南昌市设计降雨量进行了重新计算，给出了设计降雨量与年径流总控制率的关系。计算的控制率见表1。

表1 不同年径流总量控制率与对应设计降雨量

将表1中采用《指南》中设计降雨量的计算结果与《指南》中给出的同样标准控制率下设计值进行对比分析可知，本次计算的控制降水量在60%、70%、75%、80%、85%的控制率下分别为16.32、22.39、26.5、31.77、39.04mm，与《指南》中给出的设计值分别相差为0.38、0.41、0.3、0.23、-0.14mm。研究发现，《指南》中的设计值和长序列降雨情况下得到的设计值很相近，两者之间的差值要小于0.5mm以内，说明当降雨系列的统计时间不同时，不同控制率下对应的设计降雨量会有差异，各个地方应该综合考虑气候变化的趋势和周期性选择合理的计算年限。但考虑到长序列数据具备较强的代表性，能更好地反映降雨的时间变化，因此，本次研究采用1951—2019年日降雨数据进行分析。

已有的研究表明，北京、广州、上海等典型城市的年径流总量控制率的对数形式与设计降雨量的拟合程度好于年径流总量控制率与设计降雨量的拟合[14]。因此本文将分别计算VCRa以及-ln(1-VCRa)与设计降雨量的拟合结果，选择最优的拟合结果模型说明设计降雨量与年径流总量控制率的关系，拟合结果如图2—3所示。

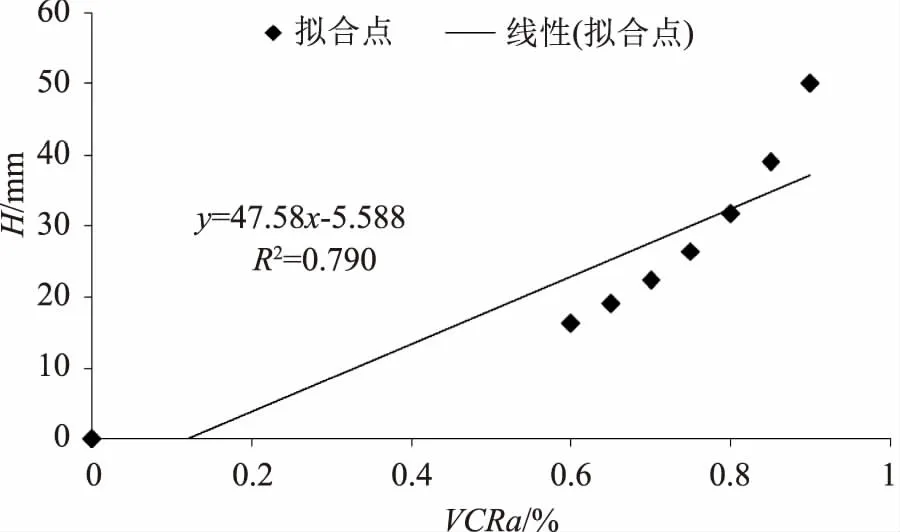
图2 VCRa与设计降雨量拟合结果

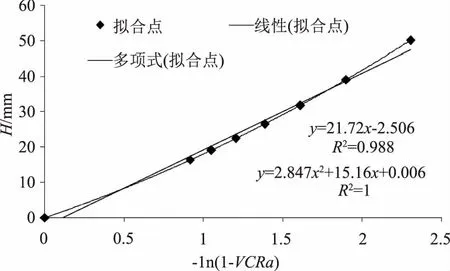
图3 -ln(1-VCRa)与设计降雨量拟合结果

从图2—3可以看出，将VCRa对数处理成-ln(1-VCRa)后与设计降雨量的拟合关系有明显的提升。同时在-ln(1-VCRa)后与设计降雨量的拟合结果中，线性拟合的R2为0.988，而多项式拟合的R2为1。因此“对数处理+多项式拟合”得到的模型H=2.847[ln(1-VCRa)]2-15.16ln(1-VCRa)+0.006可以很好的描述南昌市年径流总量控制率与设计降雨量的关系，这与邹寒等[13]人的研究结果是一致的。

3.2 年单样本设计方法下的设计降雨量

本文在实际计算中，将各控制率下的降雨数据按从大到小的升序排列并计算经验频率，并按P-Ⅲ型分布曲线进行适线，计算出均值(Ex)、离势系数(Cv)和偏态系数(Cs)。各控制率的参数见表2。

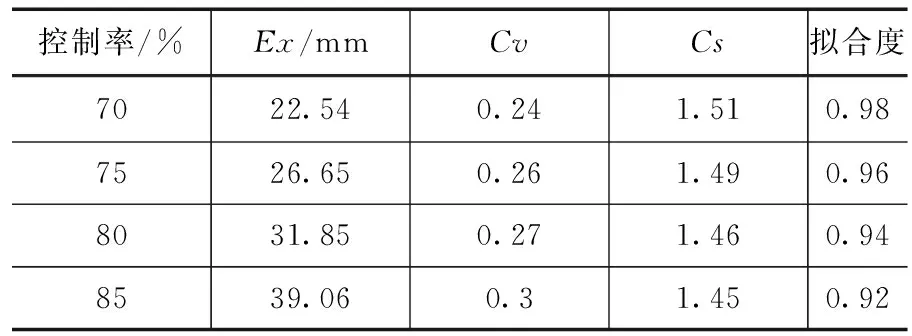
表2 各控制率下逐年单样本降雨P-Ⅲ型曲线参数

通过各降雨控制率下的P-Ⅲ型分布曲线，可给出设计频率下的设计降雨，也可算出在该设计降雨下的低影响开发设施对年内降雨总量控制的概率。本文列出10%、20%、50%、75%、80%、90%、99.99%设计值下的设计降雨，结果见表3。表3中采用的是70%、75%、80%、85%降雨总量控制率下对应的年样本值，其设计值的表征意义以任何一年中70%、75%、80%、85%的年降雨总量各自得到控制的可能性大小。若用80%降雨总量控制率分析，选择设计降雨量频率的50%，则此频率下对应的设计降雨量为29.84mm，表明在任何一年里，实现总降雨量目标80%的可能性只有50%。若按90%频率选择设计降雨量，则为23.01mm，且任意一年只有10%的可能性实现80%的降雨总量控制目标。

表3 各控制率下的设计降雨量及频率

3.3 两种不同设计方法的比较

为了将两种不同设计方法下的设计降雨量进行更加直观的比较，把表1中多年平均法计算的结果及其相应频率也列在表3中。从表3可以看出，多年平均法的设计降雨值比较接近于年单样法计算的系列均值，降雨总量控制率在70%、75%、80%、85%下的多年均法计算设计降雨量概率分别为41.04%、40.93%、40.67%、40.43%。这一方面说明按多年平均法进行降雨量设计能反映统计年份的平均降雨水平；另一方面，也反映了基于该设计雨量的低影响开发设施对单个年降雨总量的有效控制的概率约60%，即在平均100年内大概有60年该设施能实现70%、75%、80%、85%控制率下的降雨总量控制，而约有40年是无法实现。

可见，基于多年平均法的设计降雨量，虽然该方法简单，容易理解和实施，但由于忽略降雨的年际变化，计算结果只能反映地区多年降雨总量的平均控制水平，没法解决未来年份控制保证率的问题，在落实年总量控制目标时存在较大的不确定性。相比之下，对应“年控制”概念的年单样本法，由于一定程度上考虑了降雨的年际变异性，其计算的设计降雨量可反映降雨量年控制水平，能够弥补“不能反映降雨年际变异性”的不足，在海绵城市工程设计时，该法能给出不同频率下的设计降雨量，实现统计意义上的“年控制”，可提高对城市的降雨控制水平的估计。