基于SFF-PLL的永磁同步电机无传感器控制*
2023-10-21韩嘉庆武志涛徐东波
韩嘉庆,武志涛,徐东波
(辽宁科技大学电子与信息工程学院,鞍山 114051)
0 引言
永磁同步电机(permanent magnet synchronous motor,PMSM)凭借其效率高、功率密度高、动态响应快、过载能力强并且定子与转子之间无滑差、易控制等优点在航空航天、轨道交通、新能源汽车等工业领域应用越来越广泛[1]。现有的PMSM无传感器控制方法可分为基于电机凸极饱和效应的转子位置观测方法和基于基波激励下电机数学模型的转子位置观测方法。
目前,在中高速区域通常采用基于基波激励下电机数学模型的转子位置观测方法,其主要包括磁链观测法[2]、扩展卡尔曼滤波器[3]、模型参考自适应[4]以及滑模观测器(sliding mode observer,SMO)[5-8]等。SMO凭借其结构简单、对干扰的鲁棒性强以及对电机参数变化灵敏度低的优点被广泛应用于PMSM无传感器控制中。传统SMO法由于滑模控制律中的开关函数具有不连续性,会造成系统存在抖振现象最终影响到电机转子位置的观测精度。为了抑制SMO的抖振现象,鲁文其、KIM等[5-7]分别使用饱和函数、sigmoid函数和双曲正切函数代替开关函数。在一定程度上,通过使用这些新的滑模切换函数可以减少抖振现象。YANG等[8]通过将一阶范数和开关函数集成到传统趋近律中,提出了一种自适应指数趋近律。虽然该趋近律可以减小反电动势中的高频抖动,但是这种指数趋近律需要复杂的参数计算。此外,由于逆变器死区时间和磁通空间谐波的影响,使得反电动势中存在大量的高次谐波信号。高次谐波信号的存在会影响电机转子位置观测的准确性,导致PMSM无传感器控制性能降低。王辉等[9]分析了逆变器非线性以及磁通空间谐波对位置观测的影响,并提出了死区补偿策略以减小位置观测误差。虽然可以使用低通滤波器来滤除高次谐波分量,但低通滤波器会造成相位延迟,导致电机转子位置观测的准确性降低。
在上述研究的基础上,本文通过在等速趋近律基础上引入指数项,提出一种基于变速趋近律的改进型滑模反电势观测器。其次,针对逆变器的非线性以及磁通空间谐波造成反电动势观测值中存在大量高次谐波信号的问题,提出了一种同步频率滤波器(synchronous frequency filter,SFF)和锁相环(phase-locked loop,PLL)相结合的方法来提取电机转子位置与速度。
1 PMSM数学模型
本文以表贴式永磁同步电机为研究对象,PMSM在α-β坐标轴下的数学模型为:
(1)
式中:uα、uβ分别表示α-β轴定子电压分量,iα、iβ分别表示α-β轴定子电流分量,L表示定子电感,R表示定子电阻,eα、eβ分别表示α-β轴反电动势分量,其表达式为:
(2)
式中:ωe为电机电角速度,θe为电机转子位置角,ψm为永磁体磁链。
2 基于变速趋近律的改进型滑模观测器
2.1 滑模反电势观测器原理
根据文献[10],SMO可以设计为:
(3)
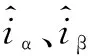
(4)
式中:k为滑模增益,且k>0;sign(·)为符号函数;将式(3)与式(1)相减可得到PMSM定子电流误差方程为:
(5)
选取滑模面s为:
(6)

(7)
2.2 基于变速趋近律的改进型滑模观测器
根据式(4),传统SMO控制律是基于等速趋近率设计的[11],即:
(8)
在等速趋近律作用下,系统在初始状态以固定速度趋近滑模面。当系统接近滑模面时,系统不会减速并稳定在滑模面上,而是在滑模面附近发生高频抖振现象。为了削弱系统抖振现象,本文提出一种变速滑模趋近律形式为:
(9)
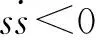
式中:k′>0,a>0,0
根据式(9)改进型滑模观测器(improved sliding mode observer,ISMO)的滑模控制律zα、zβ设计为:
(10)
根据式(3)和式(10),ISMO设计为:
(11)
(12)
其导数应该满足:
(13)
由式(10)和式(12)可得:
(14)
所以,满足式(13)的充分必要条件为:
(15)
3 基于SFF-PLL的转子位置和转速观测
此外,由于逆变器死区时间和磁通谐波的影响,反电动势中存在高次谐波信号。高次谐波信号的存在会影响电机转子位置观测的准确性,导致PMSM无传感器控制性能降低[13]。本文提出了一种同步频率滤波器(synchronous frequency filter,SFF)和锁相环(phase-locked loop,PLL)相结合的方法来提取电机转子位置与速度。
3.1 同步频率滤波器(SFF)
SFF用于滤除高次谐波分量,SFF的原理如图1所示。
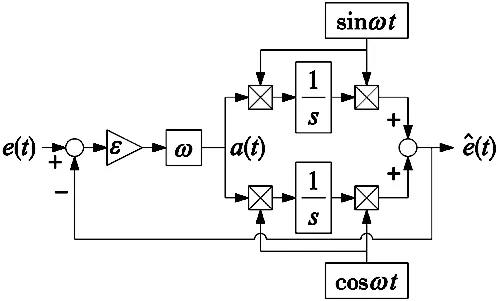
图1 同步频率滤波器原理图
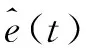
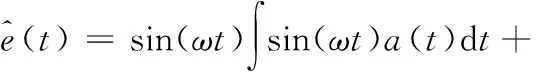
(16)
式中:
(17)
由式(16)和式(17)可以得到SFF的闭环传递函数为:
(18)
由传递函数G(s)可知,其极点为:
(19)
由劳斯-赫尔维茨稳定判据可知,当ε>0,ω>0时,传递函数G(s)的两个极点保持在复频域平面左半面。SFF的Bode图如图2所示。
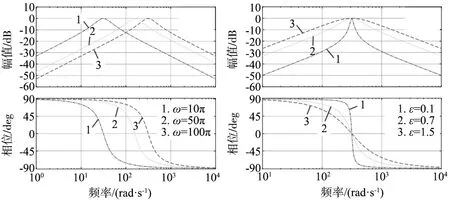
(a) ε=0.707,ω取不同值时的Bode图 (b) ω=100π,ε取不同值时的Bode图图2 同步频率滤波器Bode图
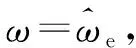
3.2 基于PLL的转子位置与转速提取
经过SFF滤波后输出的反电动势观测值可以表示为:
(20)
将SFF输出的反电动势观测值作为PLL的输入信号,如图3所示。
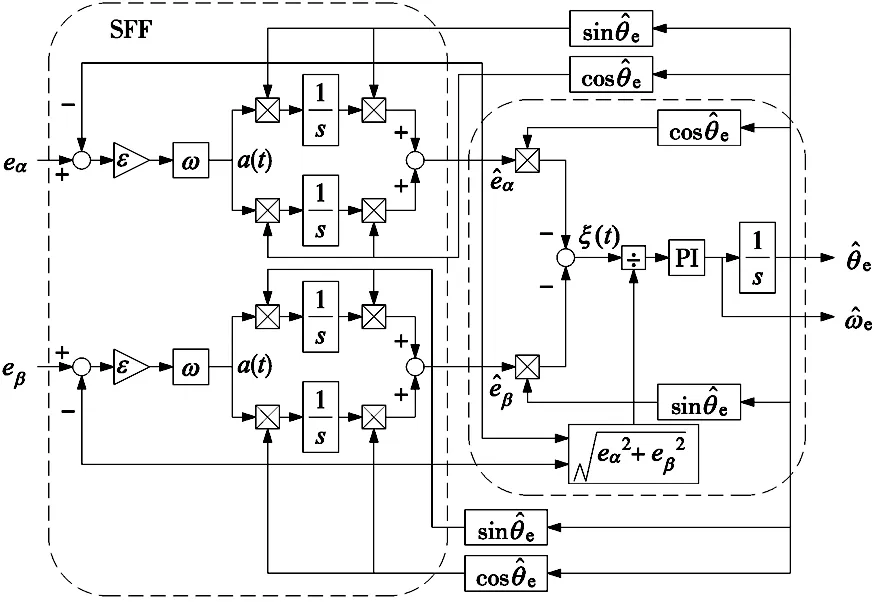
图3 基于SFF预处理的PLL框图
由图3结合式(2)可知,基于PLL的PMSM转子位置观测误差表示为:
(21)
由式(21)可得PLL的等效框图如图4所示。

图4 PLL等效框图
由图4可知,锁相环的闭环传递函数和误差传递函数分别为:
(22)
(23)
式中:kp为PI调节器的比例系数,ki为PI调节器的积分系数。当电机稳定运行时,PLL的稳态误差可以表示为:
(24)
综上所述,本文提出的基于SFF-PLL的永磁同步电机无传感器控制系统框图如图5所示。
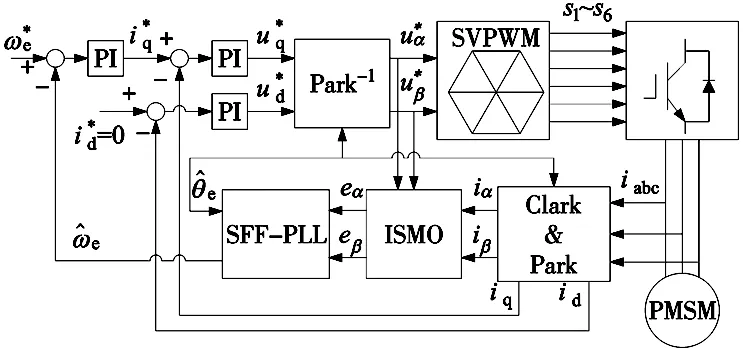
图5 基于SFF-PLL的PMSM无传感器控制系统框图
4 实验与分析
为验证本文提出的基于SFF-PLL的永磁同步电机无传感器控制的有效性,在如图6所示的实验平台进行验证。使用直流电源为PMSM控制系统提供直流电压,选用TI公司的TMS320F28069的DSP芯片作为电机控制处理器,同时采用N38-06-N型600线增量型旋转编码器测量电机真实速度,用于实验的PMSM参数如表1所示。

图6 PMSM实验平台

表1 电机参数
4.1 反电动势信号分析实验
电机运行在1000 r/min时,基于ISMO对反电动势进行观测,分别采用PLL及SFF-PLL方法对反电动势进行处理及FFT分析实验结果如图7和图8所示。

图7 基于PLL的反电动势分析 图8 基于SFF-PLL的反电动势分析
由图7a反电动势观测值的波形图可知,基于PLL的无传感器控制得到的反电动势波形存在明显的畸变。由图7b可以看出反电动势波形中含有大量的5、7次谐波。对比图8a与图7a可以看出,图8a中的反电动势波形光滑且正弦度更高。对比图8b与图7b可以看出,基于SFF-PLL无传感器控制得到的反电动势波形中含有的5、7次谐波得到明显抑制。由上述实验可得,SFF可以有效抑制反电动势中的高次谐波分量。
4.2 稳态实验
额定负载下电机运行在1000 r/min 时,分别采用PLL及SFF-PLL无传感器控制得到的转子位置和转速响应曲线如图9~图10所示。
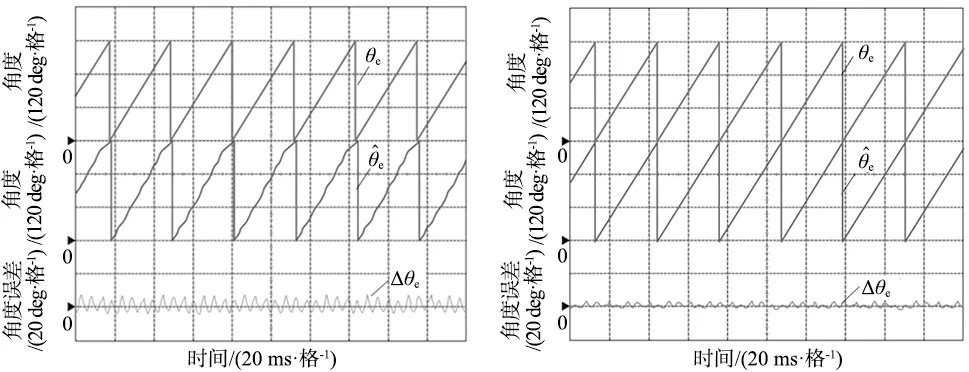
(a) 基于PLL的PMSM转子位置观测值与实际值 (b) 基于SFF-PLL的PMSM转子位置观测值与实际值图9 PMSM稳态位置观测
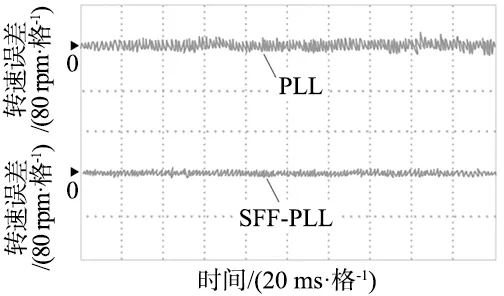
图10 PMSM稳态转速观测
由图9a可知,基于PLL的PMSM转子位置观测波动较大,由于反电动势存在畸变使得电机转子位置观测产生震荡,最大电机转子角度观测误差达到8.5°。由图9b可知,基于SFF-PLL的PMSM转子位置观测波形平滑,观测误差减小至1.9°。
由图10可知,基于PLL的PMSM转速观测与实际转速误差为31 r/min,且转速波动较大。基于SFF-PLL的PMSM转速观测与实际转速误差减小至11 r/min。由此可见,基于SFF-PLL的PMSM无传感器控制策略对转子位置和转速观测精度更高。
4.3 动态实验
额定负载下,电机转速从1000 r/min加速至1200 r/min最后减速至1000 r/min,分别采用PLL及SFF-PLL无传感器控制得到的转速响应曲线如图11所示。
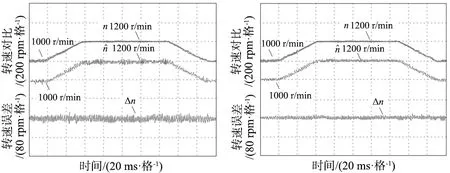
(a) 基于PLL的PMSM动态转速观测值 (b) 基于SFF-PLL的PMSM动态转速观测值图11 PMSM动态转速观测
由图11a和图11b可知,基于PLL的PMSM在1000 r/min到1200 r/min之间加减速时实际转速与观测转速的最大误差约为35 r/min,基于SFF-PLL的PMSM在1000 r/min到1200 r/min之间加减速时实际转速与观测转速的最大误差约为10 r/min。实验结果表明,本文提出的基于SFF-PLL的PMSM无传感器控制策略有效提高了电机转速动态变化过程中的控制品质。
5 结论
本文提出了一种基于SFF-PLL的PMSM无传感器控制方法。首先,提出一种变速趋近律作为改进型滑模观测器的控制律,所提出的变速趋近律可以使观测器获得更快的趋近速度;其次,提出了一种SFF和PLL相结合的方法来提取电机转子位置与速度,SFF可以有效抑制反电动势中的高次谐波分量。实验表明基于SFF-PLL无传感器控制可以使反电动势波形中含有的5、7次谐波得到明显抑制,并且在稳态和转速动态变化过程中,可以有效提高转子位置和转速的观测精度。
