不同弯曲方法对辊弯成形回弹的影响研究
2023-10-21孙玮隆张若青
韩 飞 孙玮隆 张若青
北方工业大学机械与材料工程学院,北京,100144
0 引言
辊弯成形(roll forming,又称冷弯成形)是一种高效、节能、节材的金属板材绿色成形技术,其主要工艺原理是:通过顺序配置的多道次成形轧辊使金属板带产生渐进的横向变形,从而制成特定截面的型材[1-2]。
回弹是辊弯成形过程中普遍存在的现象,准确研究工艺参数对回弹的影响是完成工艺设计的前提条件,也是在生产过程中控制加工成本、提高产品精度的关键因素。 国内外学者从不同角度对辊弯成形过程中的回弹现象进行了研究:PANTHI等[3]、谢延敏等[4]从材料特性着手,对比了屈服应力、弹性模量、硬化系数等材料力学性能和圆角半径、弯曲角度等几何参数以及时间对回弹量的影响,阐述了板材的回弹机理;ABVABI等[5]研究了超高强钢辊弯成形中板材内部残余应力对成形精度的影响,其研究结果表明,成形过程中所产生的残余应力会大幅影响板材的总变形量及塑性变形占比,进而对板材最终的回弹产生影响;BHATTACHARYYA等[6]在理论分析和试验的基础上,分析了U形件在辊弯成形过程中过渡区长度与板材厚度、弯曲角度增量和边腿长度之间的关系;BUI等[7]以辊弯成形机组为研究对象,分析了在不同道次间距、成形速度和摩擦系数下,板材变形过程中各点位的位移轨迹和纵向应变,以及这些参数对回弹量的影响;BIDABADI等[8-9]研究了辊弯成形工艺参数、产品截面形状、冲孔尺寸、润滑等多种因素对最终产品精度的影响,结果表明,工艺参数中的弯曲角度增量是影响回弹的主要因素;韩飞等[10]研究了定长度设计方法下辊弯成形在单/多道次成形过程中弯曲角度增量对回弹的影响,即最终角度一定的情况下,随着弯曲角度增量的降低,回弹呈现减小趋势。
赵金龙等[11]对比了“定长度法”和“定半径法”在成形U形件时的成形性能:定半径法具有设计简单,模具互换性好,回弹小等优点,缺点在于变形集中于弯角区域,板材应变量大,能源消耗也比定长度法大。BADR等[12]对比了两种弯曲方法对Ti-6Al-4V合金V形件成形质量的影响,得出用“定半径法”成形的工件边缘纵向应变更小、产品所得到的纵向弓和回弹量更小的结论。TRAUB等[13]通过试验与仿真的方法,测量了不同弯曲方法下,U形件弯角区域弧长以及中性层位置的变化,证明相对弯曲半径是影响弯曲区域应变分布和中性层位置的主要因素。
总体而言,目前对辊弯成形的研究主要集中于工艺参数对回弹的影响分析,关于弯曲方法的研究较少,且实践过程中主要依赖于设计人员的经验,缺乏有效的理论指导。本文通过理论分析、实验与有限元仿真的方法对辊弯成形中不同弯曲方式(定长度法与定半径法),不同圆角半径、板材厚度下产品最终的回弹量进行了测量与计算,分析得出了其相应的影响规律。
1 辊弯成形弯曲方法原理分析
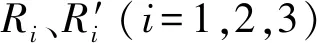
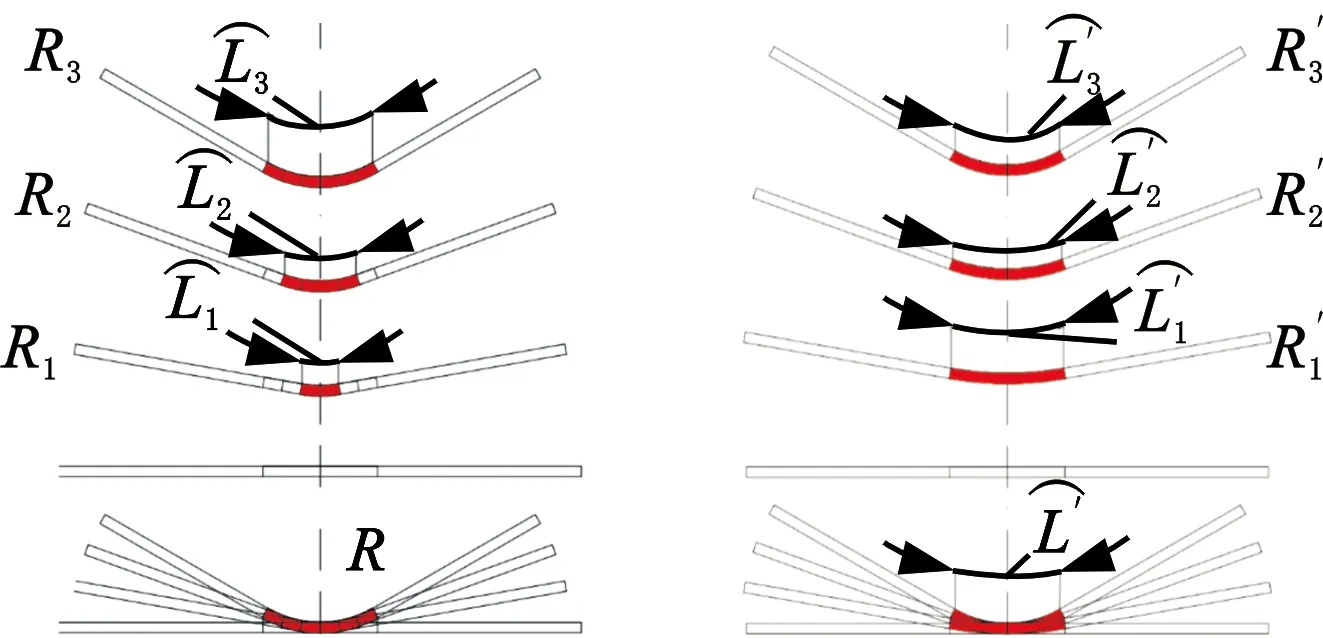
(a)定半径法 (b)定长度法图1 弯曲方法成形原理Fig.1 Forming principle of bending method
2 试验与仿真
2.1 试验平台
辊弯成形试验基于图2所示的北方工业大学辊弯成形机组进行。

图2 辊弯成形试验机组Fig.2 Roll forming experimental unit
辊弯成形试验完成后板材通过AT公司C5-CS系列一体式3D传感器扫描获取截面几何形状以获取相对应的几何尺寸,如图3所示。

图3 视觉识别检测Fig.3 Visual recognition detection
试验采用B750HL高强钢材料,通过使用Instron5982型拉伸试验机对试样进行准静态拉伸试验获得材料力学性能,应变计使用德国Gom公司的Digital Image Correlation。拉伸试件尺寸参考GB/T 228. 1—2010《金属材料拉伸试验第1部分:室温试验方法》。B750HL材料性能参数如表1和图4所示。

表1 B750HL材料性能参数
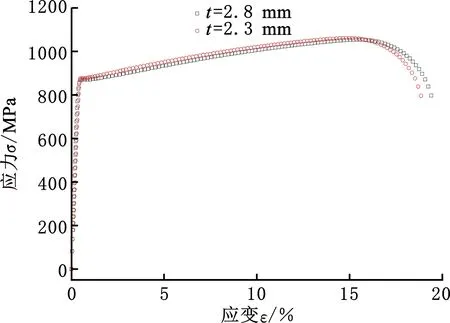
图4 B750HL应力-应变曲线Fig.4 B750HL stress-strain curve
2.2 试验方案
为探究不同弯曲方法对辊弯成形回弹的影响,设计了表2所示的正交试验。其中,R代表定半径法,A代表定长度法;A10-2.3表示定长度法、圆角半径10.00 mm、板材厚度2.3 mm方案,其余类推。
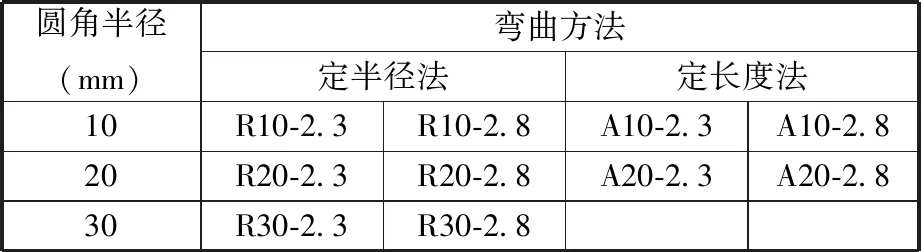
表2 正交试验方案及代号
准确计算板材弯角区域在辊弯成形过程中的圆角半径与弯曲段弧长是保证试验精度的重点设计因素。图5为板材在辊弯成形过程中的弯曲区域变形示意图,其中,点划线代表板材中性层,在成形过程中中性层长度始终不发生变化。
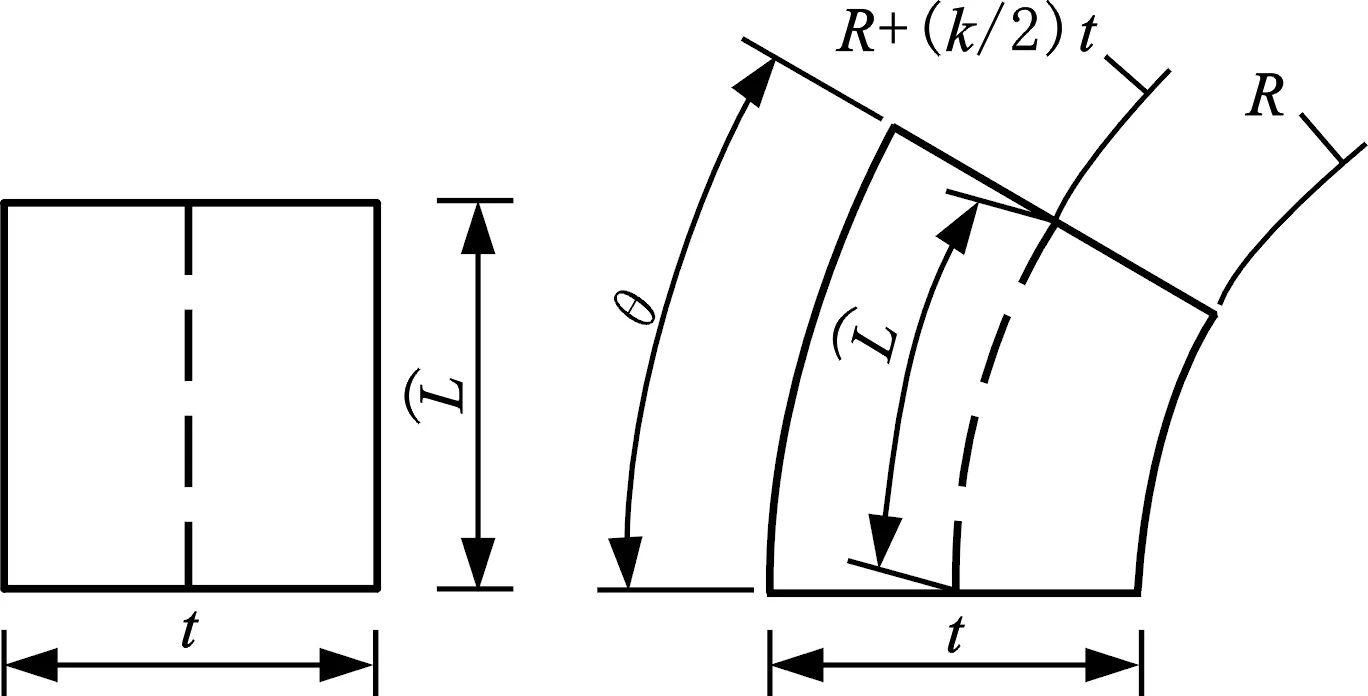
图5 辊弯成形弯曲区域变形示意图Fig.5 Schematic diagram of deformation in bending area of roll forming
由上述模型推导得到以下公式以计算板材中性层的弧长:
(1)
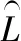
进而得到弯曲区域的理论弧长。
已有研究[14-16]表明,在径厚比R/t大于4的情况下,可以认为中性层近似处于板材厚度方向上的中间位置,即中性层系数为1。因此,为简化计算,本文设置中性层系数为1。
依照上述原理,设计有不同圆角半径对应的辊花图与轧辊共5组。辊花图如图6所示,设计基准为板材下表面弯角区中心,各道次弯曲角度增量均为10°,最终成形角度为30°。

图6 辊花图Fig.6 Strip deforming graph
根据辊花图以及辊弯成形原理设计了图7和表3所示的轧辊。其中,两种弯曲方法下,圆角半径相同的最终成形道次即第三道次(成形角度30°)中的截面和轧辊在设计中保持一致。各组试验中,同一成形角度的下轧辊共用,上轧辊辊径偏差不大于5%。
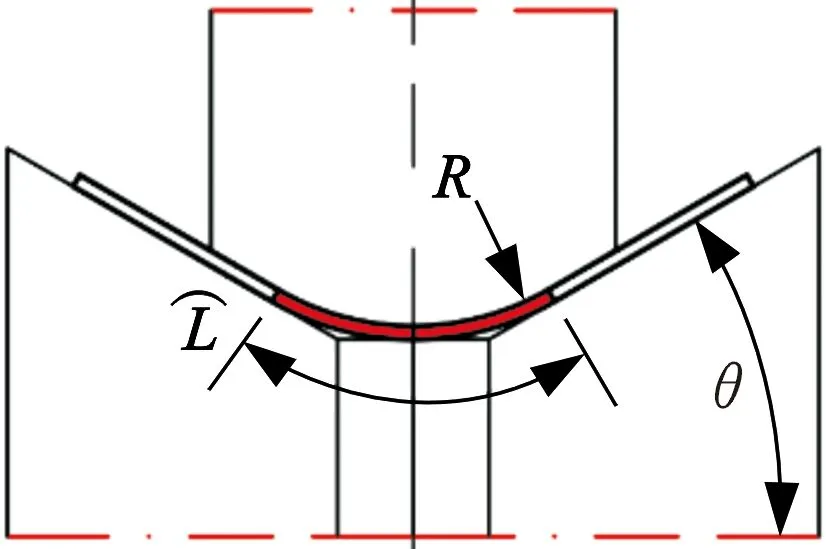
图7 配辊示意图Fig.7 Schematic diagram of roll distribution
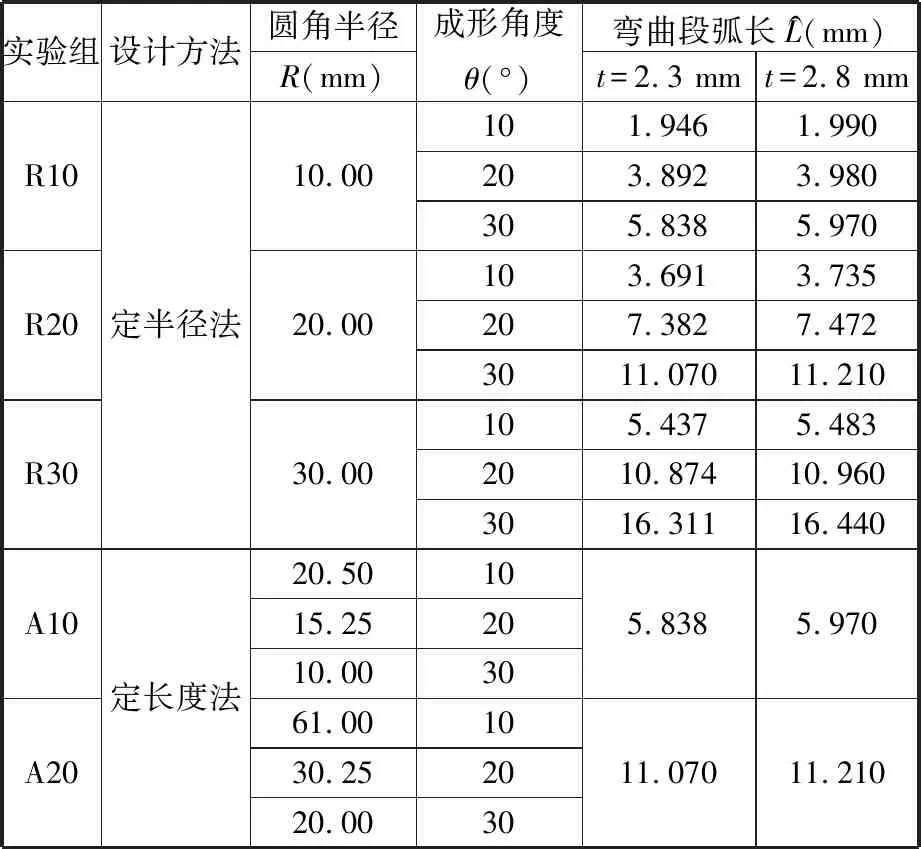
表3 轧辊设计参数
试验均采用单机架成形,下轴驱动,转速50 r/min;板材在当前道次完成成形与测量后进行下一道次的成形。
2.3 有限元模型建立
根据有限元理论设定假设条件,采用理想化轧机、安装以及调试状态。使用有限元软件Abaqus中的Explicit模块对辊弯成形过程进行仿真模拟。
仿真模型如图8所示,轧辊使用解析刚体,依照实物尺寸建模并进行相应的简化,道次间距600 mm,板材厚度为2.8 mm和2.3 mm,板宽70 mm,板长1000 mm。单元类型选用缩减积分C3D8R实体单元,材料参数由2.1节中准静态拉伸试验获得。轧辊与板材接触类型设置为摩擦接触,摩擦因数为0.02。

图8 有限元仿真模型Fig.8 Finite element simulation model
如图9所示,由于V形件辊弯成形过程中变形主要产生于板材中部的弯角区域,两侧边腿区域理论上不发生变形,因此,将板材弯角区网格平面尺寸细分为0.1 mm×5 mm(Y×Z)。并且,为防止网格大小突变导致仿真过程中可能出现的畸变现象,板材边腿区网格宽度(Y)从0.1 mm递增至2 mm。为区分拉伸-压缩形变区域,板材厚度方向划分4层网格。
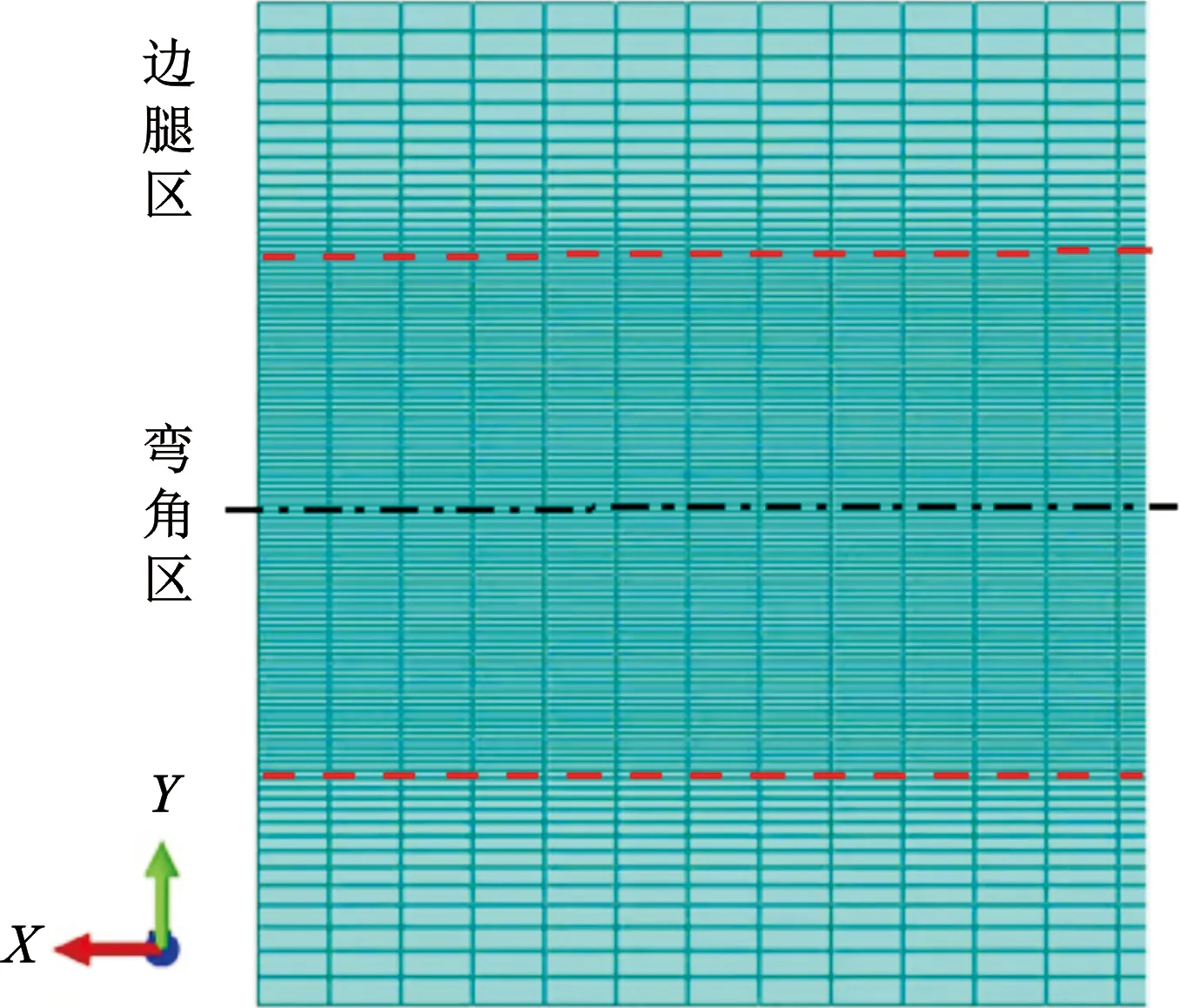
图9 板材网格划分Fig.9 Sheet grid division
2.4 有限元仿真模型验证
表4所示为t=2.3 mm B750HL板材在三道次成形后实际试验结果与仿真结果的对比,可知成形角度的试验与仿真的偏差平均值为1.46°(4.87%),最大偏差值为1.82°(6.05%),偏差率均小于10%,可认为有限元仿真精度满足要求。
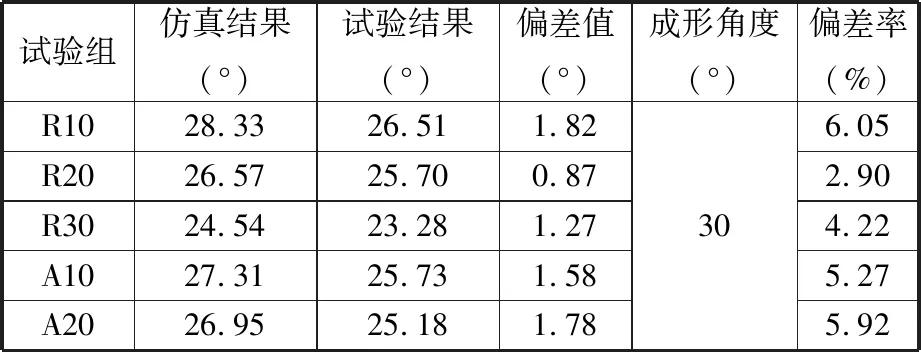
表4 试验与仿真成形角度对比
图10所示为采用定半径法,圆角半径20 mm、板材厚度2.3 mm情况下的仿真与试验截面形状对比。
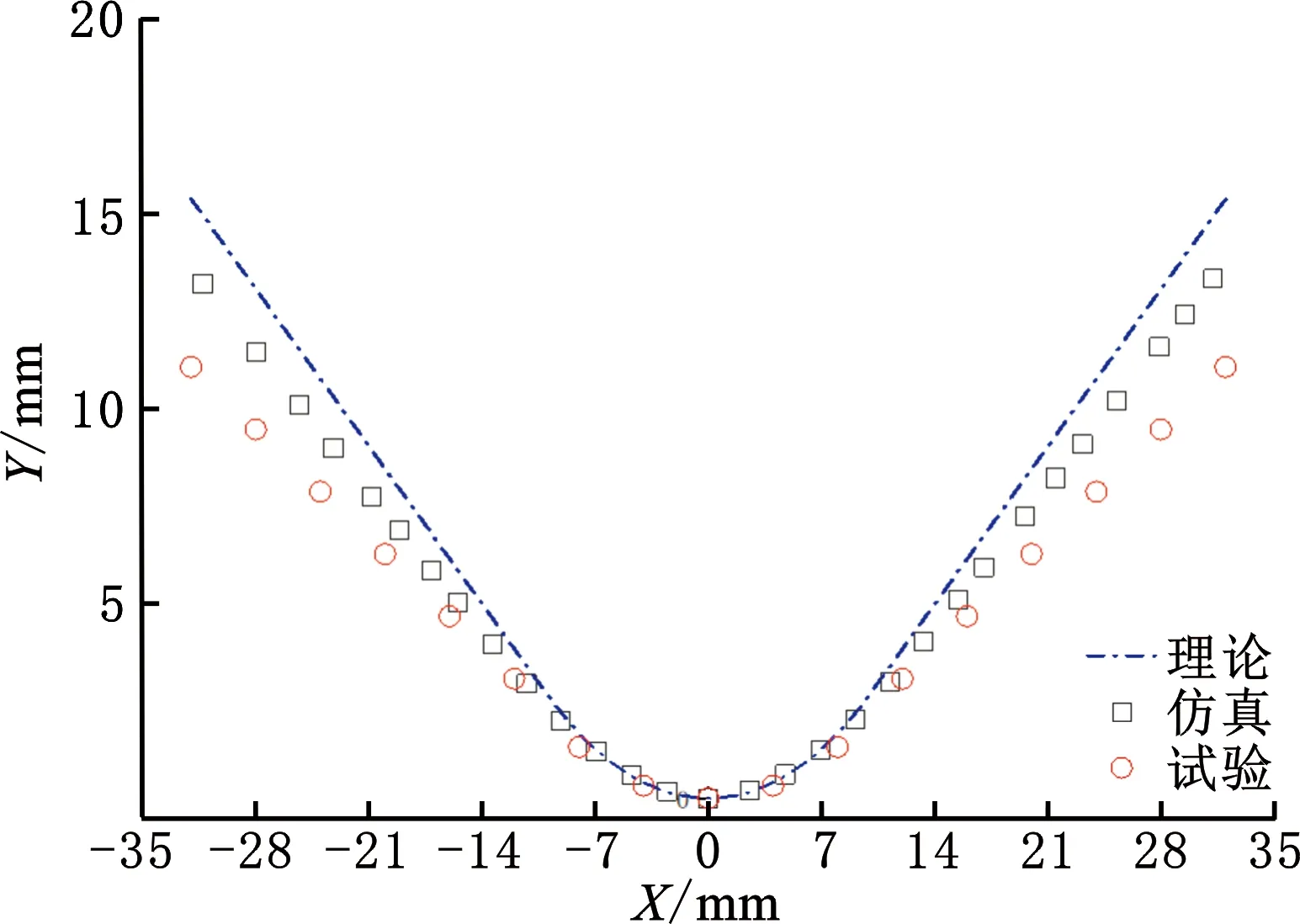
图10 有限元仿真模型实验验证Fig.10 Experimental verification of finite element simulation model
3 结果与分析

图11 辊弯成形件回弹分析Fig.11 Springback analysis of roll-formed parts
测量成形完成后的板材中间区域,取角度平均值,计算得到不同工艺参数组合下的回弹量δ,结果如表5所示。
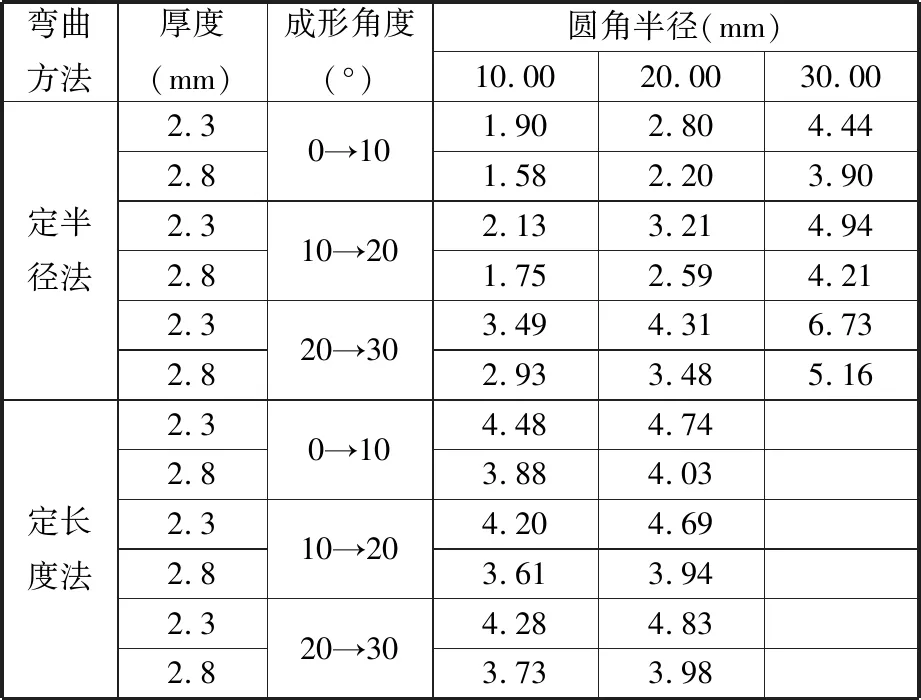
表5 不同工艺参数组合下的回弹量δ
3.1 弯曲方法对回弹的影响
辊弯成形是连续的弯曲成形工艺,板材的最终成形是多道次共同影响的结果。板材最终截面相同的情况下,由于不同弯曲方法设计原理存在差异,故最终板材的回弹量与应力-应变分布会呈现出不同的变化趋势。
图12所示为分别采用定长度法与定半径法(圆角半径20.00 mm,板材厚度2.3 mm)时三道次试验结果对比,可以看出,采用定长度法各道次的回弹量大体相同,而采用定半径法回弹量随着道次数的增加而增大,且增幅也存在上升趋势,但回弹量均小于定半径法下的回弹量。
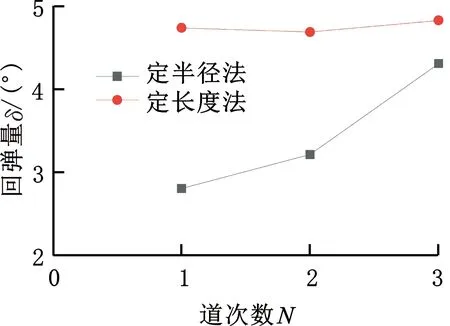
图12 试验结果(不同弯曲方式)Fig.12 Test result(different bending method)
图13所示为不同弯曲方法下各道次应变云图及其在辊缝处宽度方向上的应变分布情况。其中,理论成形区分界长度与表2中弯曲段弧长一致。
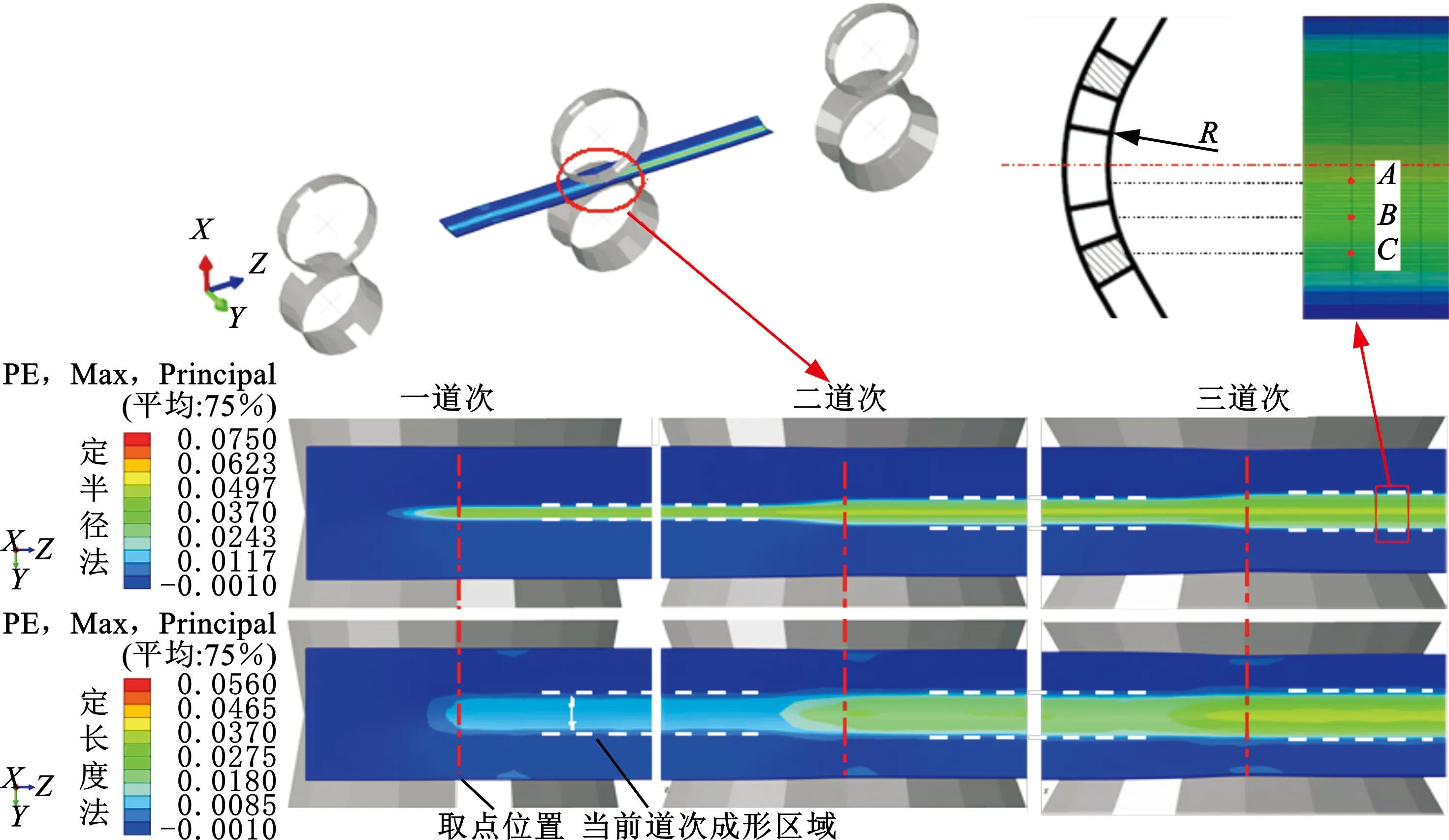
(a)三道次塑性应变云图
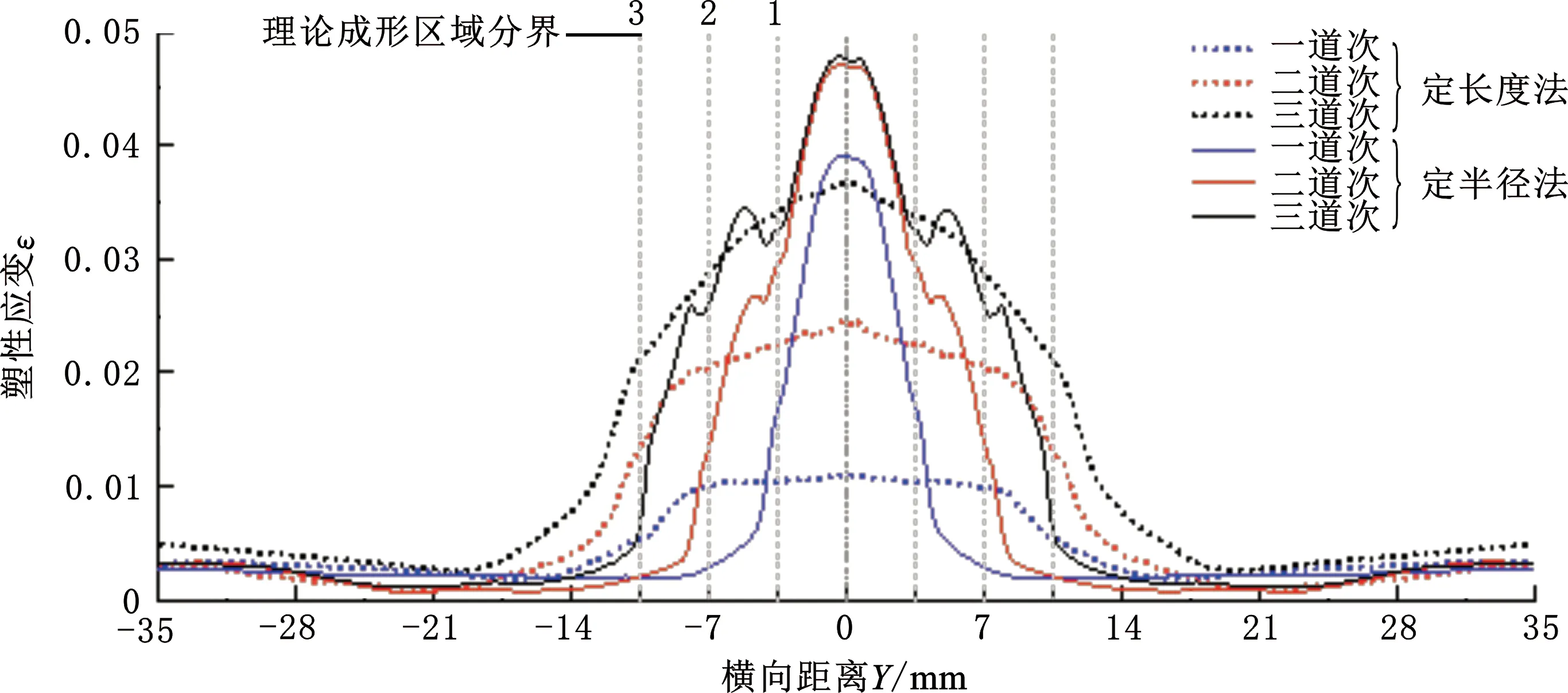
(b)板材宽度方向塑性应变分布图13 不同成形方法下各道次塑性应变Fig.13 Three-pass Plastic strain nephogram of each in different method
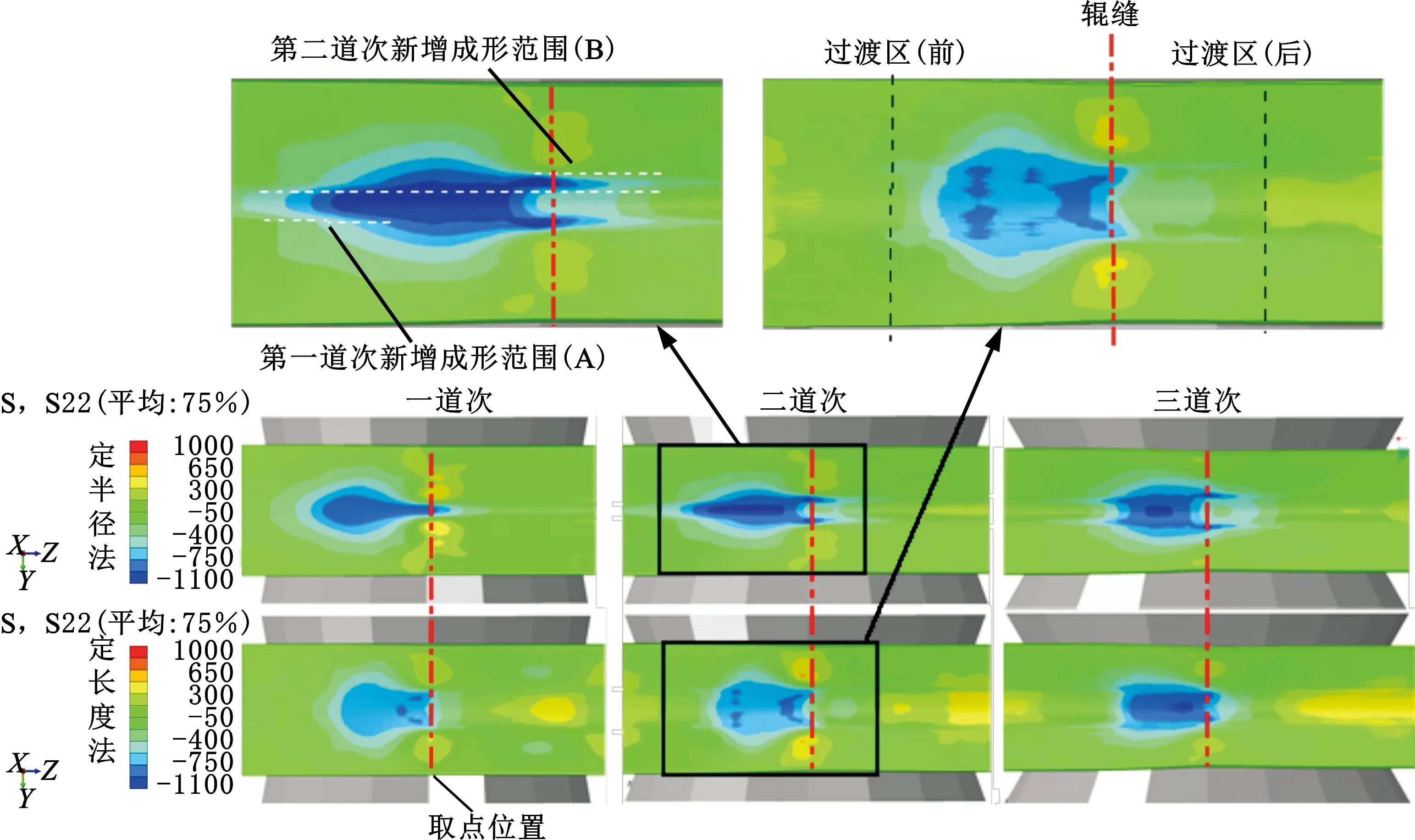
定半径法下,板材的成形区域随道次数(成形角度)的增加而扩大,产生了新的成形区域,各道次的应力峰值点出现于各道次新增理论成形区域中心;应变集中于板材中心,依照不同成形区域呈现类似阶梯状的分布。
而与之相对,在定长度法下,三个道次中的应变主要分布区域,即成形区域大小基本一致,在其范围内分布较为均匀;随着道次数的增加,各道次轧辊圆角半径值减小,理论形变量增大,应变幅值也随之增大,且随着道次数的增加,板材内的应变也逐渐集中至板材弯曲区域中心。
对比两种成形方法下第三道次的应变幅值可以看出,定半径法下,板材内积累的应变幅值(峰值0.048)较定长度法下(峰值0.036)大,成形程度更高,从而出现其总回弹量较定长度法下总回弹量小的情况。
辊弯成形是典型的增量成形工艺,板材最终的变形是经过多道次变形累计达到的结果。如图13a右上所示,在板材上表面弯角区取A、B、C三点,分别对应定半径法中不同的弯曲区域中心,其横向应变随辊弯成形过程变化规律如图14所示。
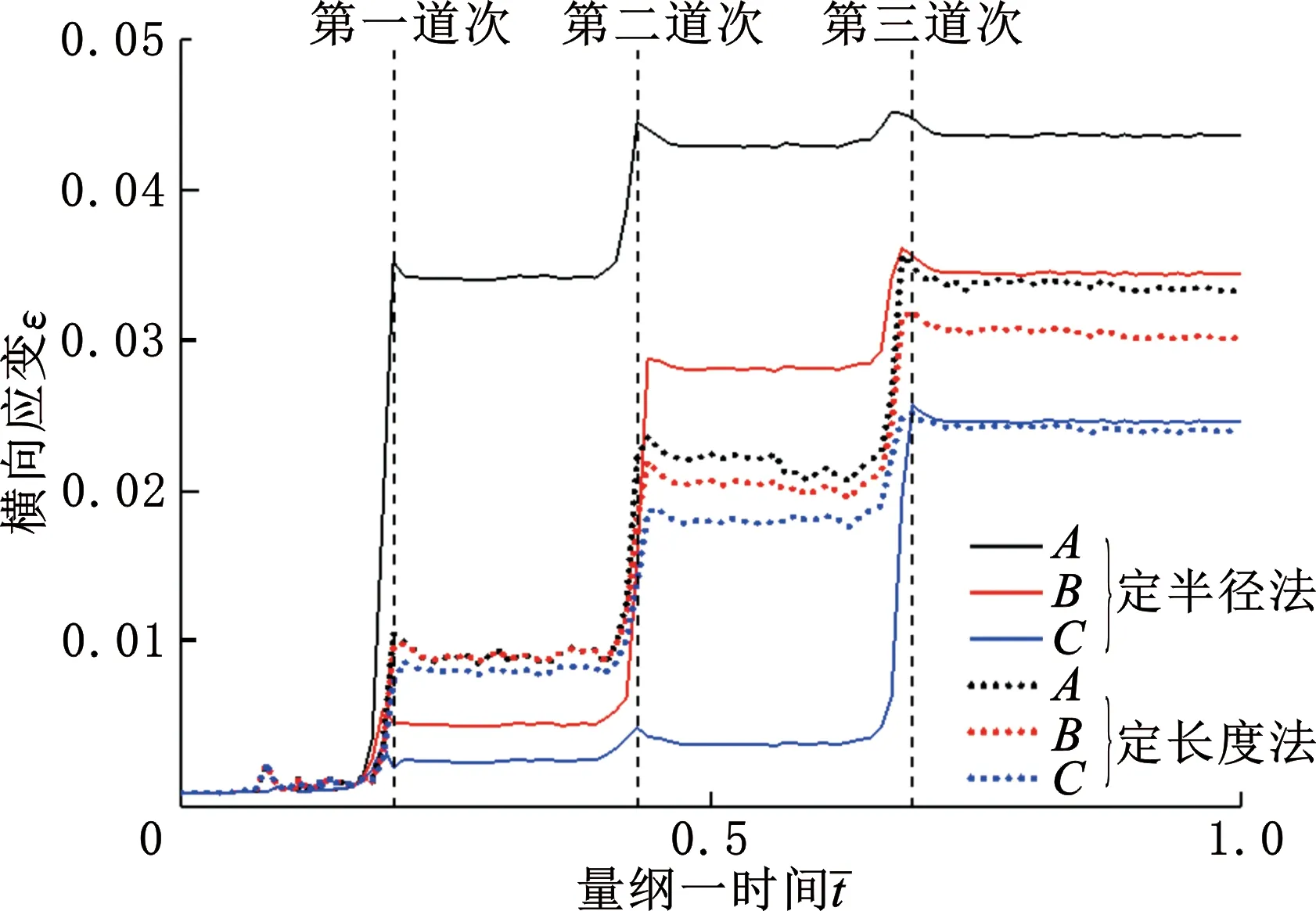
图14 横向应变随时间变化Fig.14 Variation of plastic strain with time
定半径法下,A、B、C点应变分别在第一、第二、第三道次出现大幅变化,说明在定半径法下,成形区域随道次数增加逐步向外扩张;A点塑性应变在第一道次成形后仍在第二、第三道次出现幅值上的变化,与之相同,B点塑性应变在第三道次也存在幅值变化,说明板材各成形区域在第一次成形并未达到最终形状,仍与设计截面存在一定差异。
定长度法下,A、B、C点近乎同时发生形变,第一道次应变幅值基本一致,差值因应变集中现象而逐渐增大,这与图13b中所示一致。
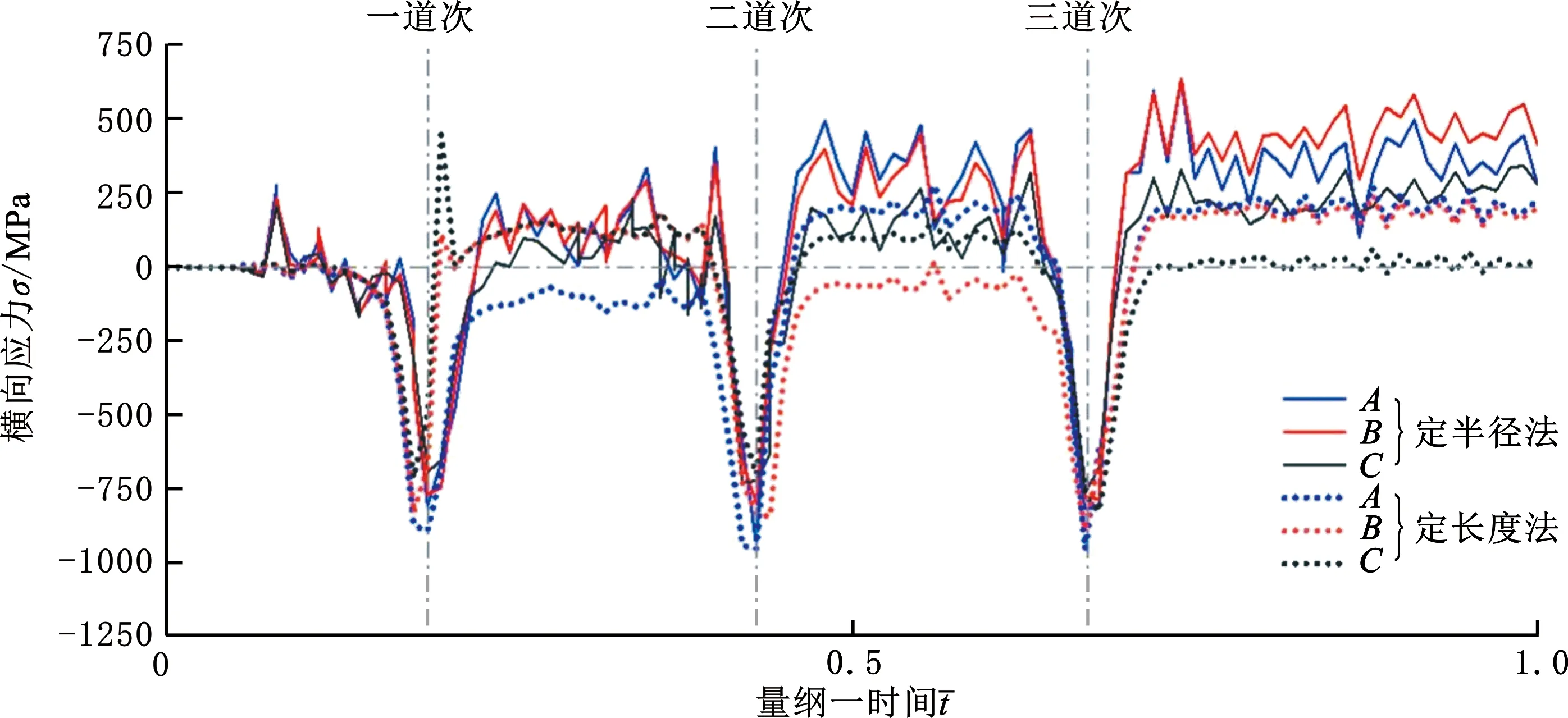
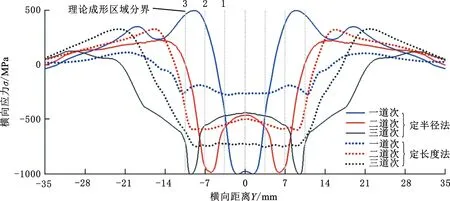
由图15所示横向应力云图与A、B、C三点处横向应力随时间变化的分布情况可以看出:两种弯曲方法下,在板材进入辊缝前,均存在在宽度方向上出现先扩大后缩小的成形过渡区,其宽度与当前道次的成形区域大小有关。
定半径法下,由于各道次的成形区弧长不同,应力分布也产生相应的变化。当前道次的未成形区域会出现更大的应力回复。以第二道次为例,进入辊缝前,A点所受横向应力始终保持负值,为受压状态;而随着板材逐渐接近辊缝,应力则集中至总成形区域的中心,此时,A点所受应力幅值大于B、C两点应力;板材在辊缝处以及离开辊缝后,应力峰值处于当前道次的新增成形区域内,即B点所代表的区域,该区域在离开辊缝后仍受到一定量的压缩应力,持续至下一道次。
定长度法下,各点位应力分布规律基本一致,仅在幅值上有所差异,板材内部残余应力随着道次数的增加而增大。
如图15c所示的辊缝处的横向应力分布情况,定半径法下,应力峰值点出现于当前道次的新增成形区域内,各道次应力峰值基本一致;定长度法下,板材所受横向应力在三个道次辊缝处的分布规律上基本一致,幅值随着道次数(形变量)的增加而增大。
过渡区长度也是反映板材回弹规律的因素之一[2],图16所示为各道次变形过渡区长度,可以看出,采用定半径法有着更长的过渡区,板材受到轧辊的弯曲作用的时间更长,从而能够更好地消除板材内的残余应力,减小回弹量。表6所示为成形完成后各节点残余应力值,较之定长度法,定半径法下的残余应力值更小,因此总回弹量更小。
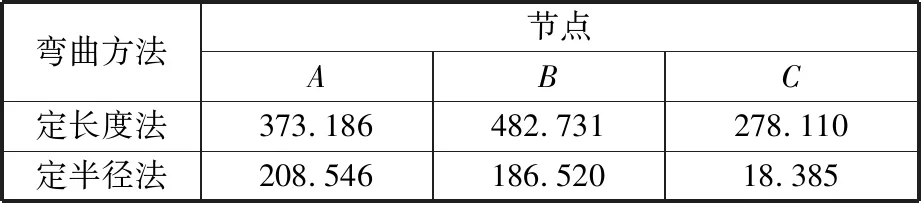
表6 成形完成后节点残余应力
3.2 不同弯曲方法下其他工艺参数对回弹的影响
3.2.1圆角半径对回弹的影响
图17所示为板材厚度2.3 mm、成形角度30°、不同圆角半径下的回弹量对比,由图可知,不同弯曲方法下,回弹量均随着圆角半径的增大而增大。
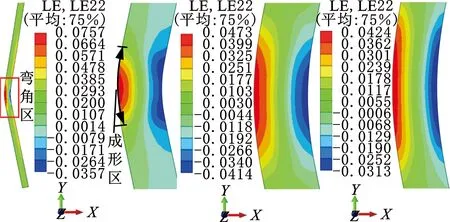
图18为采用定半径法时不同圆角半径下的横向应变云图,可知:随着圆角半径的增大,板材的最大横向应变量降低,且弹性应变占比增大(图19)。同时,成形区域也随圆角半径的增大而增大,即回弹作用的区域增大,两者共同作用使得回弹量不仅随圆角半径的增大而增大,增幅也随之增大。
3.2.2板材厚度对回弹的影响
图20所示为在圆角半径20.00 mm、成形角度30°、两种弯曲方法下不同板材厚度的试验结果,相比之下,厚度2.3 mm板材回弹量较厚度2.8 mm板材的回弹量偏大。两种方法下回弹量的变化趋势相同。
(a)三道次横向应力云图
(b)横向应力随时间变化
(c)各道次辊缝处板材宽度方向横向应力分布图15 不同弯曲方法下各道次的横向应力Fig.15 Transverse stress distribution of each pass in different bending method
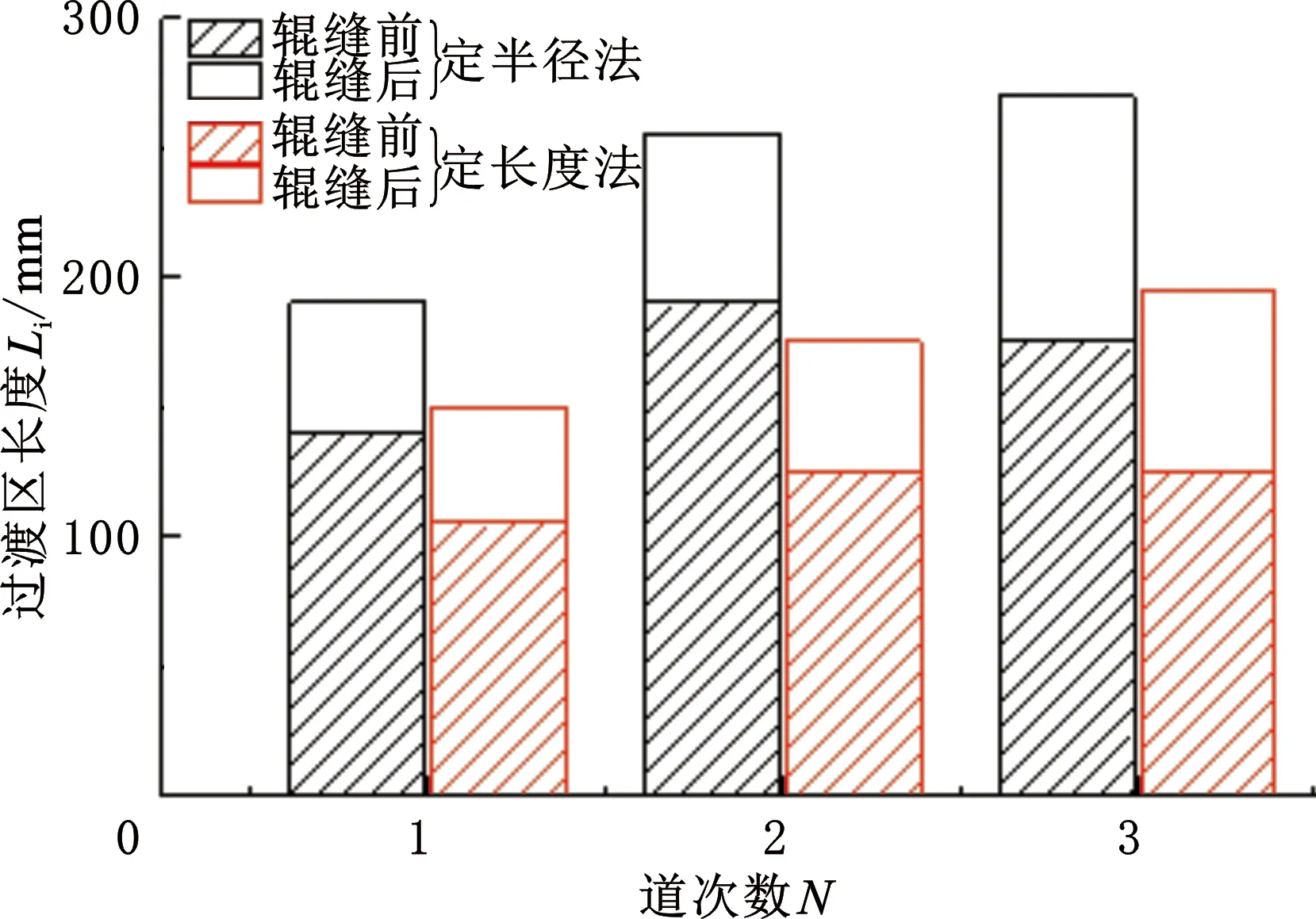
图16 过渡区长度Fig.16 Length of transition zone
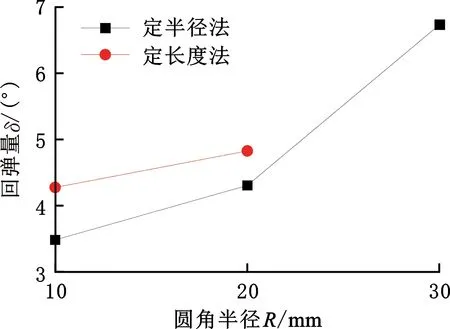
图17 试验结果(不同圆角半径)Fig.17 Test result (different section fillet radius)
(a)R=10.00 mm (b)R=20.00 mm (c)R=30.00 mm图18 不同圆角半径下横向应变云图(定半径法)Fig.18 Transverse strain nephogram of plate cross section under different bending radius (constant bend radius method)

图19 不同圆角半径下第一道次最大横向应变量与弹性应变占比(定半径法)Fig.19 Proportion of maximum transverse strain and elastic strain of the first pass under different fillet radii (constant radius method)
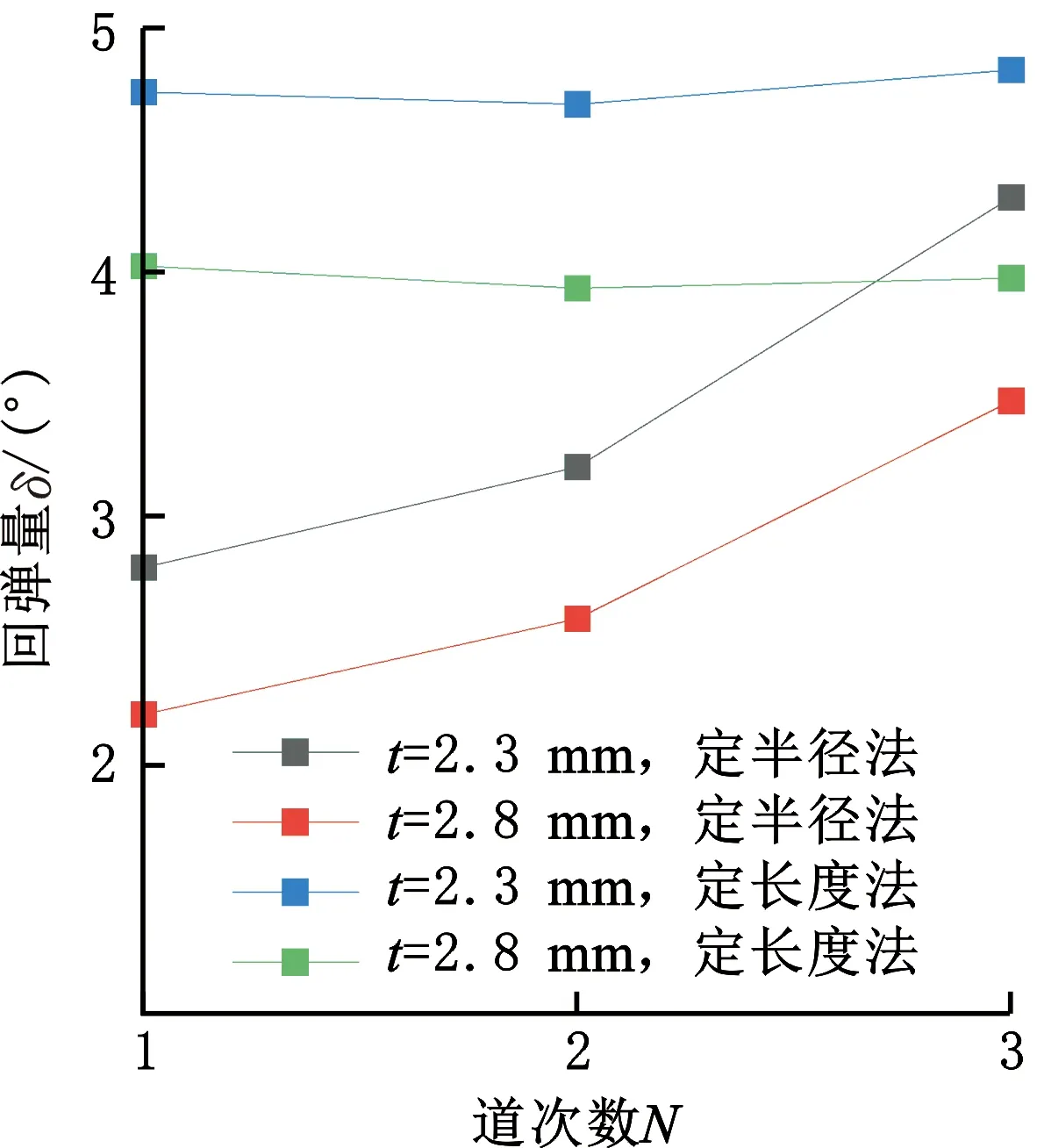
图20 试验结果(不同板厚)Fig.20 Test result (different plate thickness)
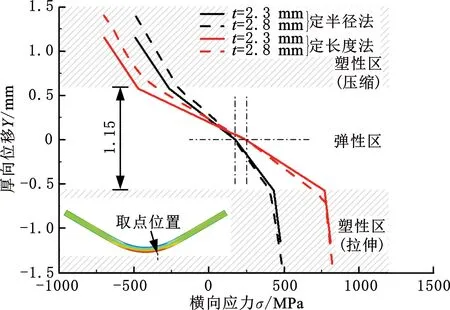
图21 第三道次辊缝处板材厚度方向上横向应力分布Fig.21 Transverse stress distribution in the thickness direction of the plate at the third pass roll gap
图21所示为相同圆角半径(20.00 mm)下,不同板厚的板材在第三道次辊缝处受到的横向应力在厚度方向上的分布情况,横向应力的变化趋势在不同区域内呈现明显差异。不同板厚下,板材内的弹性区域大小基本一致。随着板材厚度的增大,板材中的弹性区域的比例减小,进而使得回弹量也随之减小。
表7中,回弹量比值与板材厚度比值大体相等,说明在两种弯曲方法下,回弹量均与板材厚度形成较为稳定的相关性,二者近似成反比关系。
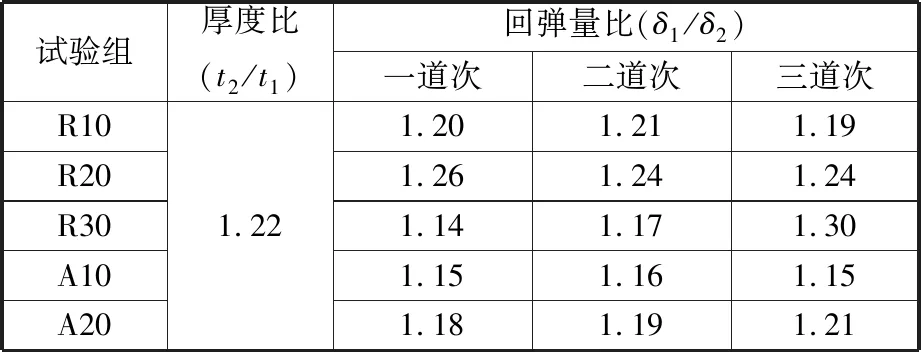
表7 不同试验组下的板厚比与回弹量比
4 结论
(1)辊弯成形是连续的弯曲成形工艺,板材的最终成形是多道次共同作用的结果。最终成形截面一致的情况下,不同弯曲方法(定半径法及定长度法)工艺原理中各道次圆角半径与弯曲段弧长的差异是影响两者回弹量以及应力-应变分布的主要因素。
(2)定半径法下,回弹量随着道次数的增加而增大,增幅也存在上升趋势;定长度法下,回弹量随道次数的增加无明显变化,且幅值总体大于定半径法。
(3)定半径法下,各道次圆角半径值不变,弯曲段弧长随道次数(成形角度)的增加而增大,成形区域也随之增大,其增量与成形角度增量成正比;各道次应变峰值处于板材中心,基于不同成形区域呈阶梯状分布;各道次辊缝处板材所受应力集中于当前道次的新增成形区域内,峰值基本一致。
(4)定长度法下,各道次成形区域(弯曲段弧长)不变,轧辊圆角半径随道次数(成形角度)的增加而减小,形变量随之增大;各道次应力与应变的主要分布区域基本不变,在成形区域内分布较为均匀;应变幅值随道次数的增加而增加,并逐步集中至板材中心;定长度法下各道次应变、应力峰值均小于定半径法下的相应值。
(5)在两种弯曲方法下,回弹量均出现随着圆角半径的增大而增大的趋势,且增幅也随之上升;回弹量随板材厚度的增加而减小,板材内部弹性区大小基本一致,回弹量比值与厚度比值近似成反比。
