面向刮底安全的电池包防护结构轻量化设计
2023-10-21成艾国张承霖于万元何智成
王 超 成艾国 张承霖 于万元 何智成
1.湖南大学汽车车身先进设计制造国家重点试验室,长沙,4100822.柳州职业技术学院汽车工程学院,柳州,545001
0 引言
随着电动汽车销量的快速增长,有关新能源车起火事件的报道也不断增多,电动汽车的安全性已成为全社会关注的一个焦点[1]。在实际使用过程中,当车辆掠过有凹坑、凸起物或者石头等不平路面时,电动汽车底部极易受到撞击和剐蹭。然而底部碰撞造成的损伤在电池底部,具有隐蔽性,甚至有些事故虽然在当时未发生短路起火,但后续安全性无法保证,因此电动汽车底部防护十分重要[2-3]。
目前国内外对电池包的底部防护研究较少,主要集中在整车级碰撞保护。PAN等[4]对使用了三种高强度钢材料的电池组外壳进行耐撞性模拟,研究了材料和厚度影响外壳耐撞性的机理。WANG等[5]在电池模组两侧安装了负泊松比防撞块,用于在侧面柱碰撞事故中保护电池模组系统。PAN等[6]在电池组外壳设计中采用先进高强度钢并进行了尺寸优化,提高了电池包的防撞性能。王国杰等[7]设计了一种典型的正面刮底碰撞工况及其碰撞壁障,并提出了两种电动汽车电池包防护优化方案,降低了电动汽车电池包在正面刮底工况中的损伤。杨威[8]对某款车的动力电池包进行了底部碰撞仿真,重点分析底部碰撞过程中,动力电池包变形失效以及箱体、内架等内部固定结构和电池模组的碰撞安全性。黄芦[9]研究了不同参数的道路异物与电池包的冲击碰撞,全面分析了动力电池包在底部冲击碰撞下的响应。
在汽车防护结构设计中,研究者已广泛运用轻质材料及多种优化方法,以满足汽车性能及轻量化的需求。WANG等[10]设计并测试了X形增强泡沫填充管在准静态轴向压缩下的性能,填充的管材具有更好的能量吸收能力。陈静等[11]为某车型设计了碳纤维复合材料防撞梁,采用全因子试验设计确定其横截面形状与铺层顺序的最优组合,应用NSGA-Ⅱ遗传算法对防撞梁结构铺层厚度进行了多目标优化。杨江林等[12]结合非线性拓扑优化方法和连续变厚度轧制技术对汽车保险杠横梁进行了耐撞性设计。曹立波等[13]采用中心复合试验设计和自适应响应面法对所设计的铝合金保险杠横梁壁厚进行了试验仿真优化。以上对防护结构的研究主要针对前端防护,对电池包刮底防护结构的优化设计较少。
本文以某汽车电池包刮底防护结构为研究对象,开展电池包刮底防护结构轻量化设计,同时考虑了防护结构的截面形状参数和布置参数对刮底响应的影响。首先,建立了电池包刮底工况及其仿真模型,并对比了钢制防护结构与挤压铝防护结构的差异。其次,通过拓扑优化确定了挤压铝防护结构的最优截面形状,对比了三种截面在不同安装位置和布置参数下的电池模组侵入量,并分析了防护结构保护电池模组的机理。最后,在满足电池安全的基础上,采用多目标海洋捕食者算法对刮底防护结构的截面及布置参数进行优化,获得最优截面及布置方案,实现刮底防护结构的轻量化设计。
1 电池包刮底工况
电池包被刮底常因路面凸起障碍物对车辆电池底板的刮蹭所致,该类型碰撞存在一个水平方向的速度,在经过障碍物时与电池包发生碰撞。通过将实际障碍物简化为立方体、长方体、蘑菇头、半球头和锥体等几类形状进行仿真分析发现,半球头导致的刮底损伤较为严重,水平撞击工况中整车最小离地间隙位置和电池包前部防护结构对该工况有重大影响[14]。
1.1 刮底工况设定
采用中国汽车工程学会发布的T/CSAE 244—2021《纯电动乘用车底部抗碰撞能力要求及试验方法》中设置的工况:刮底工装为φ150 mm的实心半球,材质为45型钢;随机选定薄弱点作为刮底初始对准位置,选择该点沿X方向进行刮底测试;刮底壁障顶部最高点相对于电池包最低点,在Z方向上的重叠量为30 mm;试验车速为沿行驶方向30 km/h。工况示意图见图1。
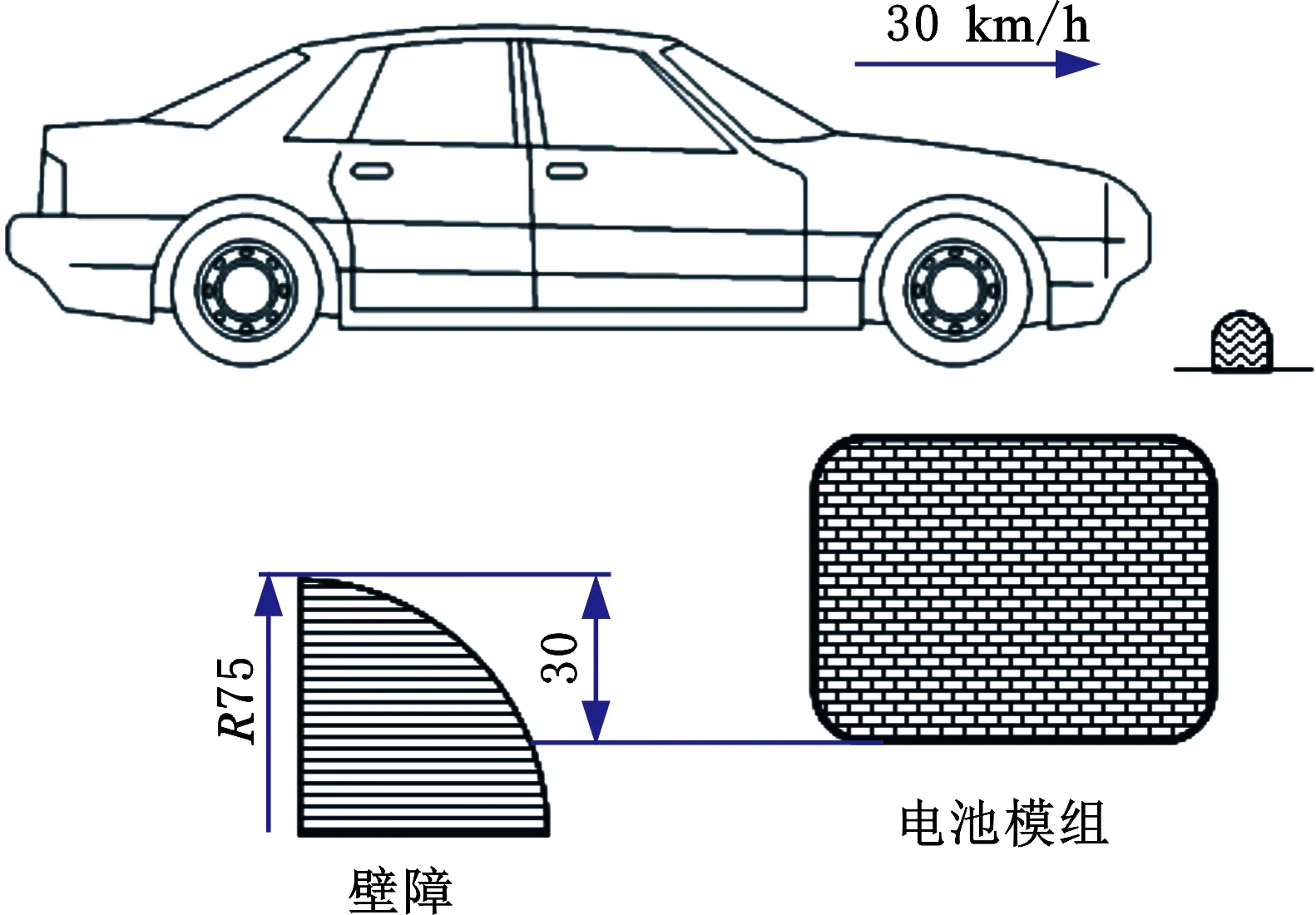
图1 刮底工况示意图Fig.1 Schematic diagram of bottom-scraping conditions
1.2 评价标准
挤压失效位移是通过挤压方式触发电池热失控的临界位移,挤压失效位移与挤压速度、挤压力关系不大,研究[15]表明,动态压痕荷载试验对电芯局部挤压位移达到5mm时,电池产生内短路。从试验结果来看,挤压失效位移与电池设计直接相关[16]。杨威[8]对方形铝壳磷酸铁锂电池进行了压缩试验和电池拆解观察,得出表征电池内部短路失效的力学参数:电池压缩变形量在4.5 mm以内安全,在4.5~6.0 mm时存在短路危险,6.0 mm以上时电池发生短路失效。综合企业标准,在仿真模型中,设定对电池模组的侵入量小于5 mm。
1.3 整车仿真模型验证
由于相关法规并未对刮底工况作出要求,因此未进行试验对标。本文基于某车型的整车正面偏置碰撞LS-Dyna仿真模型,通过整车正面偏置碰撞的试验与仿真对比,验证整车碰撞模型的准确性,然后基于此模型,根据1.1节的工况设定,搭建刮底仿真模型。对比分析车辆B柱下方加速度传感器所测得的加速度曲线可知,试验和仿真的加速度曲线在整个碰撞过程中基本吻合,同时试验与仿真最大加速值分别为49g和47.7g,指标差异较小,满足仿真试验对标的精度要求,具体结果如图2a所示。整车结构变形和试验对比结果如图2b所示,两者的碰撞变形模式基本一致。

(a)加速度曲线对比

(b)变形模式对比图2 试验与仿真结果对比Fig.2 Comparison of experimental and simulated results
当前装配的电池模组为刀片电池,每个电芯单体厚度为15 mm,采用20 mm×15 mm×20 mm的六面体单元模拟,材料模型为MAT63,电芯单体之间隔断及外壳采用壳体单元模拟,材料模型为MAT24。搭建的电池包刮底工况模型及仿真结果如图3所示(考察电池模组在垂直方向(Z向)的侵入量)。侵入量测量方式为:依次在电池模组上,每隔50 mm建立局部坐标系,并单独测量每个坐标系下50 mm内的单元在垂直方向的侵入量,取最大值。仿真结果表明,最大侵入量位于模组前端位置,最大值为13.76 mm。

(a)仿真模型
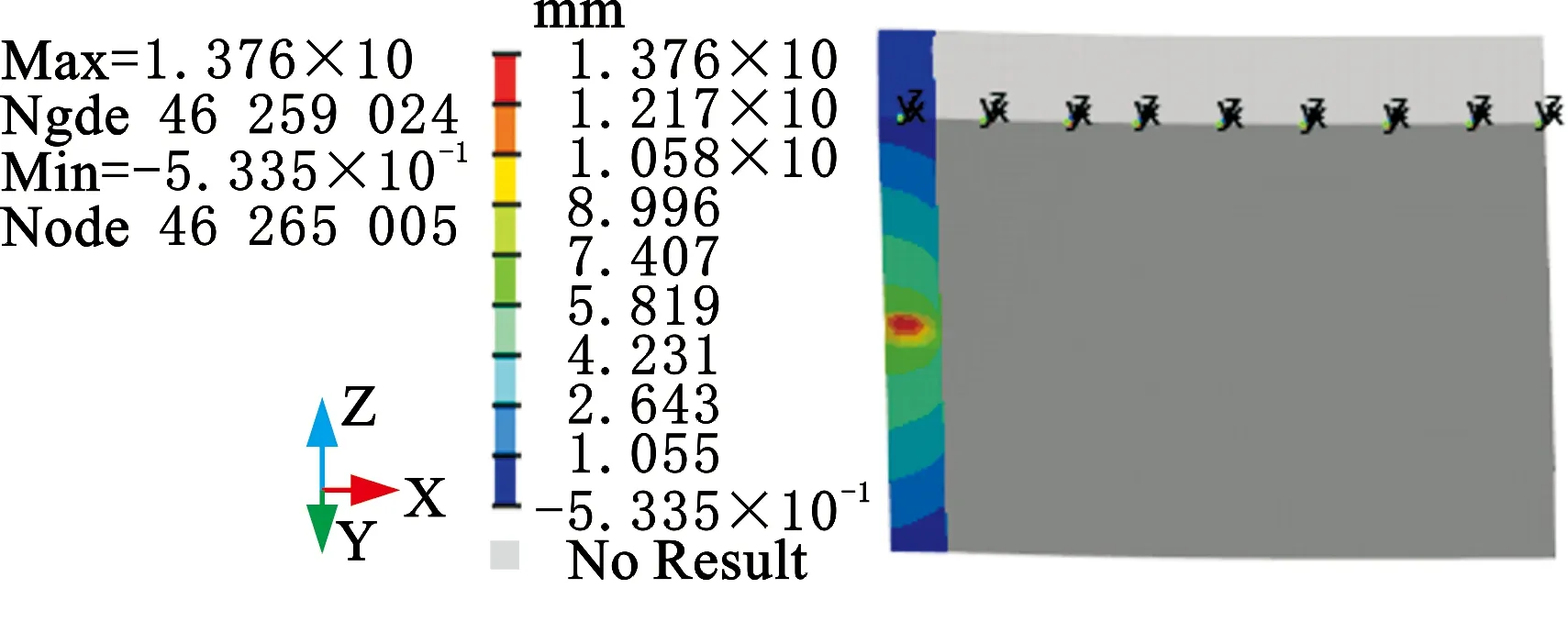
(b)模组侵入量测量图3 模组侵入量仿真结果Fig.3 Simulation results of the module intrusion
1.4 钢制与铝合金防护结构对比与验证
原钢制防护结构安装在车底雪橇板位置,主体为钢管结构,质量为2.5 kg。经分析可知,原钢制防护结构增大尺寸及厚度后,质量增加到8 kg才可以满足不大于5 mm的侵入量要求。
此车型的前防撞梁已准备使用6063-T6材料,因此本文拟采用6063-T6挤压铝型材代替钢制防护结构。两种结构的安装位置、截面尺寸与材料如图4所示。考虑到风阻及安装的因素,将铝制防护结构的底面设计为圆弧结构,上层为保证安装需求设计为平面,长度尺寸与钢制结构保持一致。由于铝材的弹性模量和屈服强度较低,因此截面宽度作了适当放大,后续进行尺寸的优化。铝制防护结构的质量为1.86 kg,相比原钢制结构减重25.6%。基于1.3节的整车刮底仿真模型,替换铝合金防护结构后的电池模组侵入量为13.90 mm,与钢制防护结构相应值差异不大。
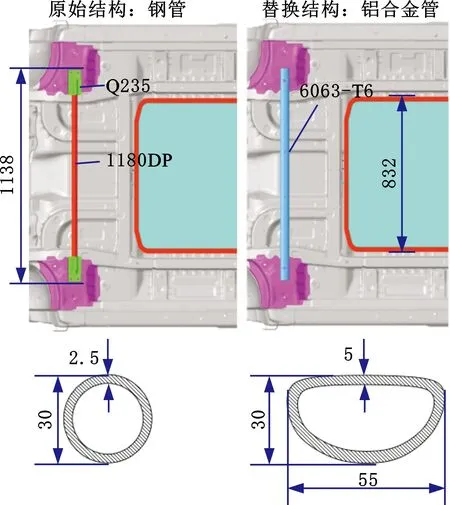
图4 防护结构安装示意图Fig.4 Schematic diagram of the installation of the protective structures
在当前的雪橇板安装位置,防护结构的长度尺寸(1138 mm)已经超过电池模组宽度尺寸(832 mm),浪费了部分材料,如图5所示,同时考虑到当前位置优化的成本较高,本文拟将防护结构安装在副车架上,以缩短长度,起到初步轻量化的效果,如图5所示。经分析可知,铝制结构安装在副车架后,质量为1.25 kg,相比原钢制结构减重50%,电池模组侵入量为7.9 mm,有明显改善。分析原因为:防护结构安装在雪橇板位置,前后上下变形空间较大,撞击过程中防撞杆被顶开,撞击后恢复初始形状,从而削弱了对车身的降速作用;防护结构安装在副车架位置,撞击过程中,副车架和防护结构均参与吸能,撞击后无法恢复。两种情况的防护结构变形模式如图6所示。
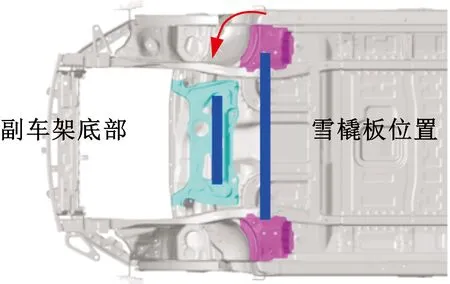
图5 防护结构的两种安装位置Fig.5 Two positions for the protective structures

图6 防护结构变形模式Fig.6 Deformation modeof the protective structures
两种防尘结构的具体连接方案分别如下:原钢管的端部通过烧焊与一个连接板连接,连接板继而与雪橇板通过两个螺栓组装在一起;由于铝合金防护结构的安装面设计成了平面,所以不需要额外的连接板,在铝管上设计工艺孔,并在副车架表面设计凸台安装平面,两者通过螺栓连接。新结构中螺栓选择M10×10.8级螺栓,可承受最大42 kN的剪切力。防护结构和副车架之间的螺栓连接通过使用9号BEAM单元模拟,BEAM单元的两端节点通过RigidBody单元分别与副车架和防护结构相连。BEAM单元的材料模型为*MAT_SPOTWELD,材料参数如下:弹性模量210 GPa,密度7850 kg/m3,泊松比0.3,采用最大剪切力(失效参数)42 kN,如图7所示。
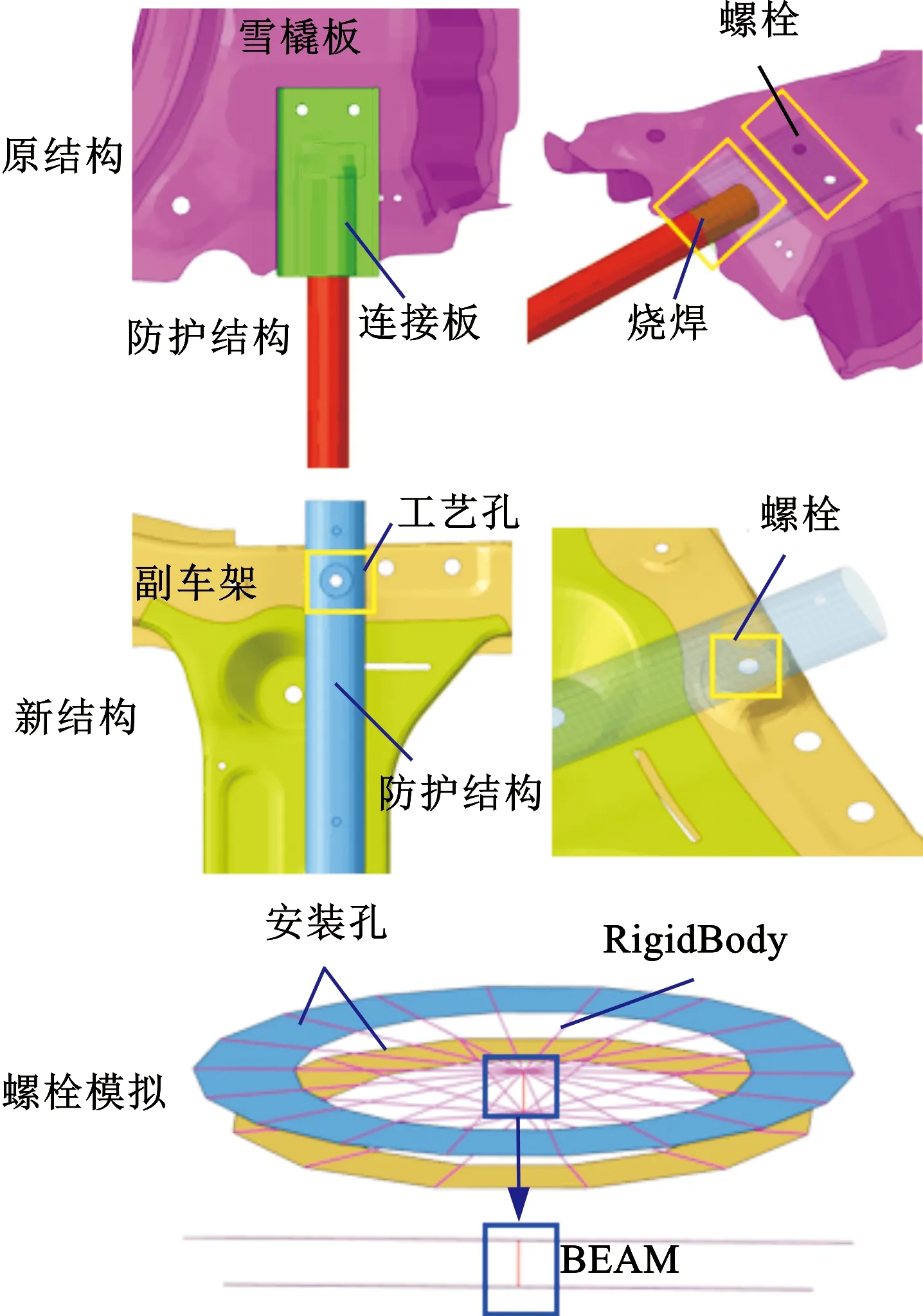
图7 螺栓的安装方式及仿真模型Fig.7 Installation method and simulation model of bolts
2 铝合金材料模型验证
本文选择厚度为3.0mm的铝合金6063-T6,采用万能试验机和高速试验机测定了不同应变率下的材料曲线,采用Swift-Hockett-Sherby本构模型描述材料的硬化行为,最终转换为真实应力-真实应变曲线,如图8所示。仿真模型中的铝合金选择MAT24材料模型,并采用等效塑性应变失效准则,材料参数为:弹性模量73 GPa,密度2700 kg/m3,泊松比0.3,失效应变0.346。通过对采用6063-T6材料挤压成形的防撞梁进行三点静压试验和仿真分析来验证铝合金材料的准确性。试验工况设置(企业技术要求)如下:防撞梁的左右安装板固定在支座上(安装方式需与实车一致),压锤中心与防撞梁Y=0重合,压锤静载向下压防撞梁使其变形25 mm,最大接触力应不小于18.9 kN。防撞梁三点静压受力仿真与试验现场如图9所示,图中SPC表示节点约束。
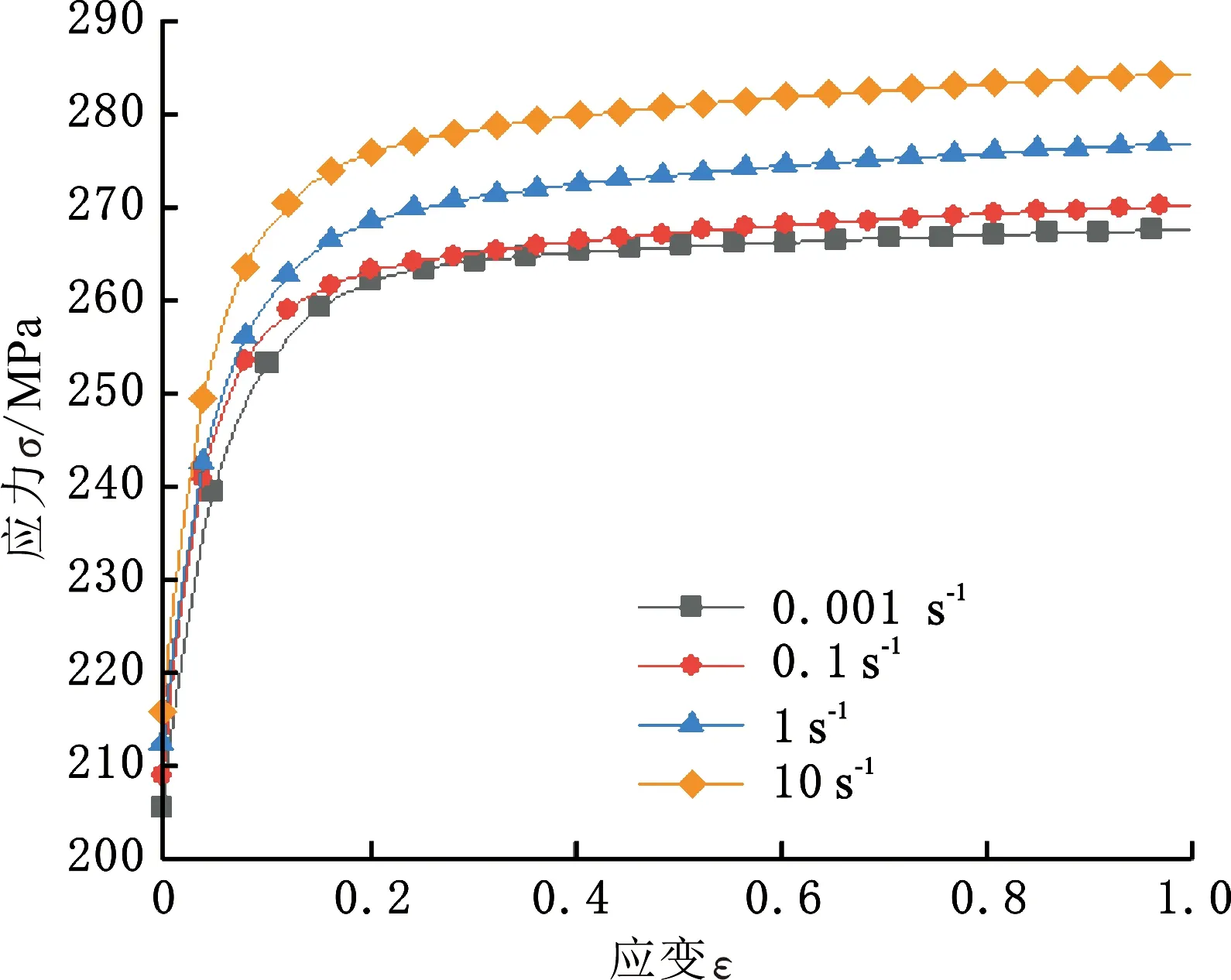
图8 真实应力-真实应变曲线Fig.8 Real stress-real strain curves

图9 防撞梁三点静压仿真及试验Fig.9 Simulation and test of three-point static pressure of bumper
图10所示为三点静压试验和仿真分析得到的支反力-位移曲线,测试样件的试验曲线与仿真曲线变化趋势一致,峰值相近。试验支反力峰值均值为22 kN,仿真分析支反力峰值为21.3 kN,两者误差为3.2%,验证了上述铝合金材料模型的准确性和可靠性。
3 铝合金防护结构设计
3.1 截面设计
电池包防护结构在接触到刮底壁障时,对防护结构在X、Z两个方向均有冲击力,因此建立的简化拓扑优化模型中,中间位置施加XZ向的集中力F,如图11中①、②所示。约束两端位置所有自由度,将防护结构内部空间填充实体网格,作为优化空间,建立的拓扑优化模型如图11中③所示。优化设置如下:目标——应变能最小;约束——体积分数不大于30%;工艺约束——施加Y向挤压约束。
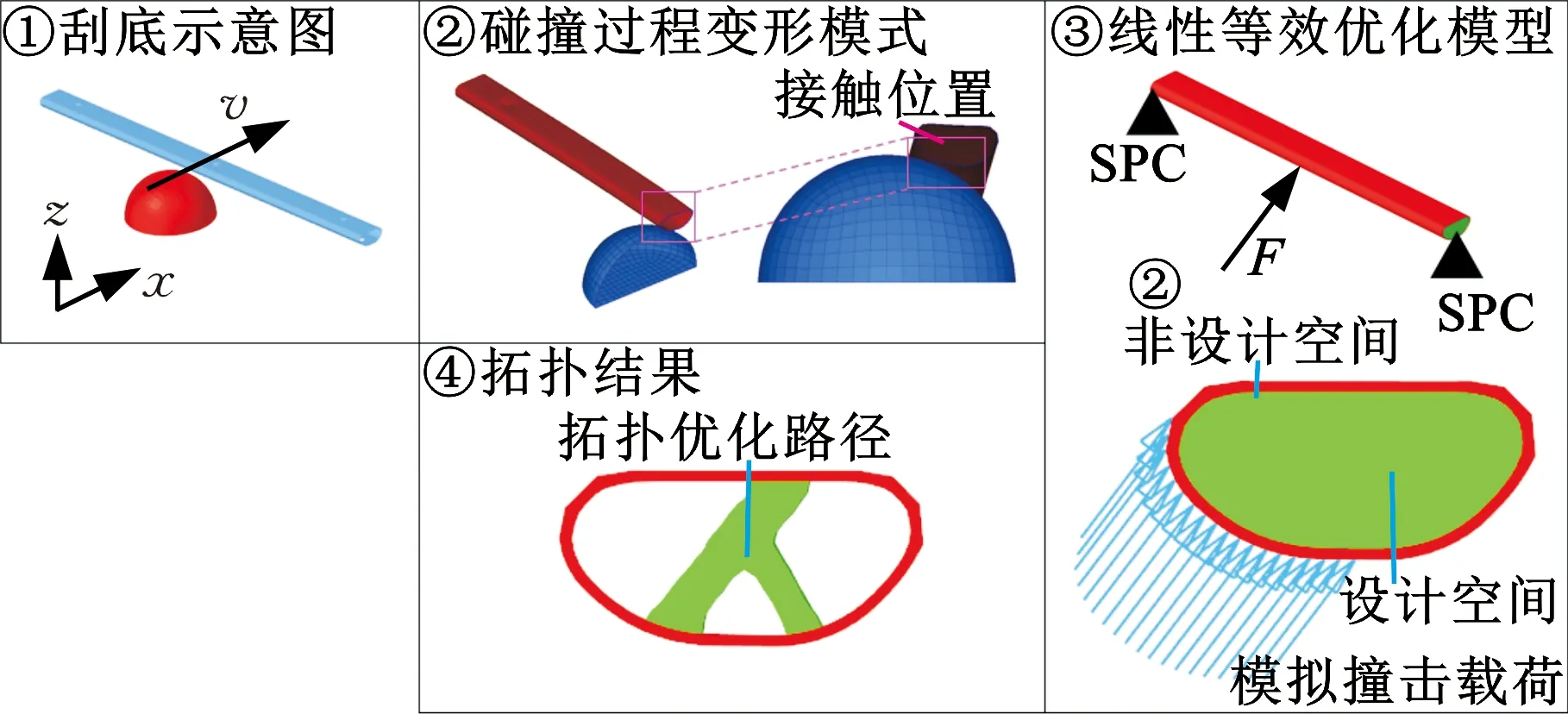
图11 防护结构截面拓扑优化流程Fig.11 Topology optimization process of protective structure section
调用OptiStruct优化求解模块计算,结果收敛后,在HyperView中得到了图11中④所示的“人”字形的材料密度分布。在受力方向实现压溃吸能,同时人字形结构增加压溃方向上的稳定性,避免提前屈曲变形。
3.2 不同截面设计对比分析
为了验证“人”字形截面防护结构的有效性,基于原始截面及拓扑优化的截面,并参考铝合金防撞梁常用的“目”字形截面,设计了三种横截面形状。三种截面的外部截面尺寸均一致,分别调整厚度,保证三种截面的防护结构质量基本一致,如表1所示。
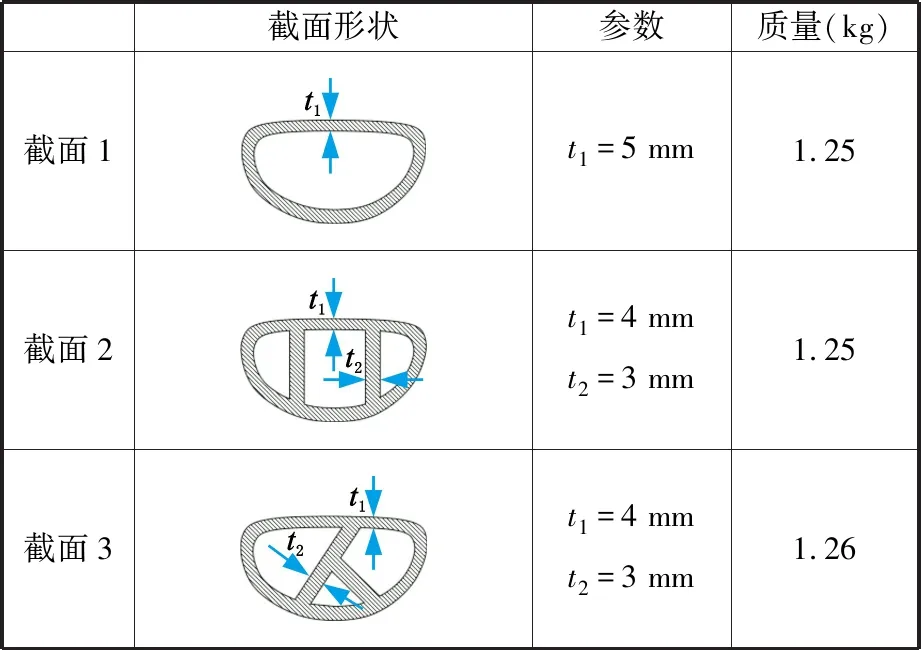
表1 三种截面形状及参数
将三种截面的铝制防护结构分别进行了整车刮底仿真分析、简化模型仿真分析(参考图11中①工况),整车刮底仿真分析考察模组侵入量,简化模型仿真分析考察能量吸收,结果如图12a所示。结果表明,虽然截面1的能量吸收高于截面2和3,但整车刮底仿真中模组侵入量却更大,说明了防护结构的优化设计不能采用类似于防撞梁简化模型的方式[13-14],需要使用整车刮底仿真模型。同时“人”字形的截面有利于改善电池包刮底性能。
3.3 不同安装位置的对比分析
对比了三种截面在副车架和雪橇板位置的模组侵入量,如图12b所示。结果表明,安装在雪橇板位置,三种截面的模组侵入量无差异,但安装在副车架位置,截面3的模组侵入量更低,说明安装在副车架位置的三种截面均优于安装在雪橇板位置。后续的验证及优化均采用布置在副车架位置的“人”字形断面的铝合金防护结构。
3.4 布置参数的影响分析
根据3.3节分析可知,防护结构布置在副车架位置时模组侵入量明显优于布置在雪橇板位置时,说明布置参数对防护结构的性能有较大影响,因此建立布置参数评估模型,如图13所示。共设置了4种参数:LB为防护结构与电池模组纵向距离,HB为防护结构与电池模组高度差,GB为防护结构与车体间隙,DB为防护结构与壁障重叠量。
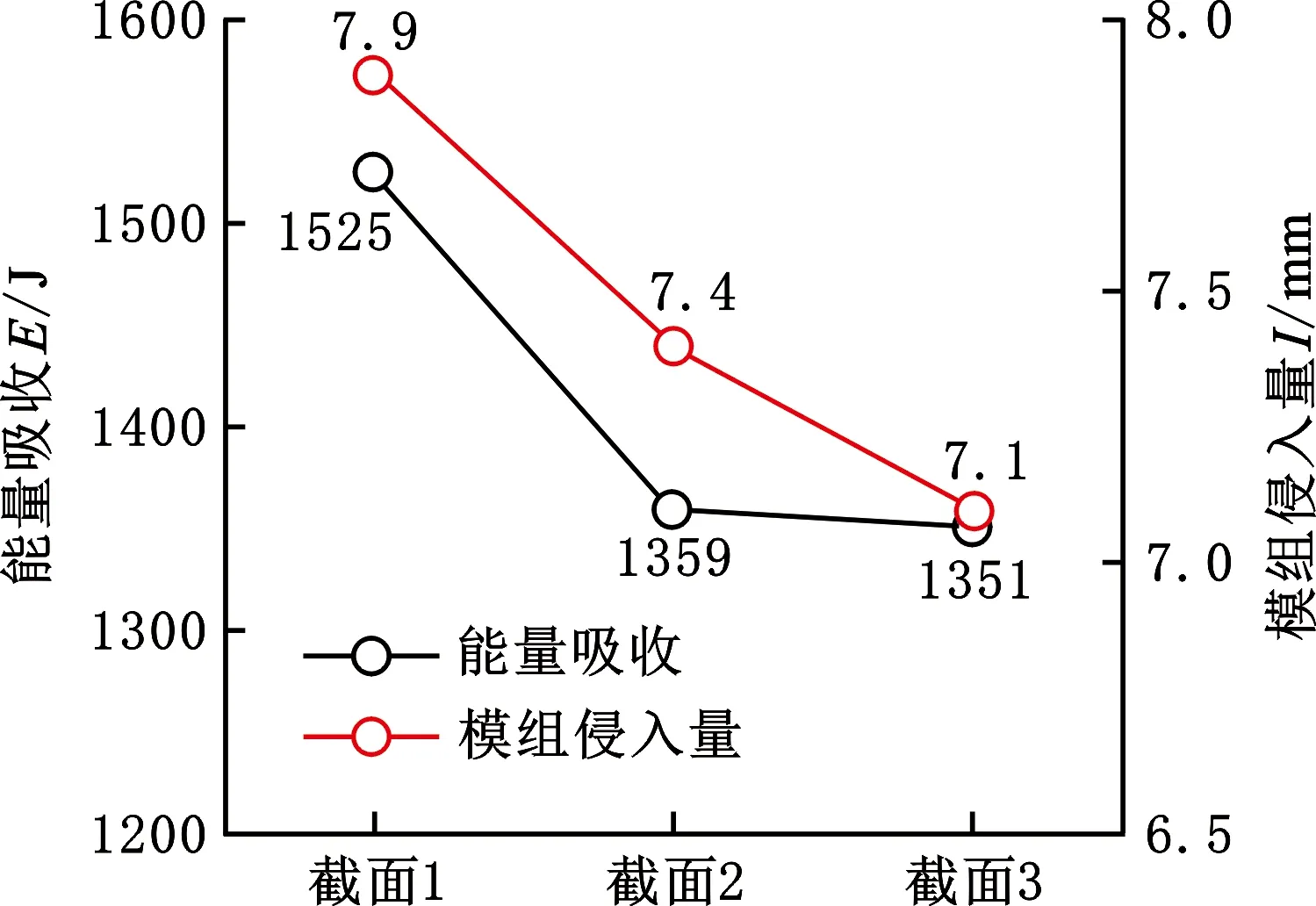
(a)吸能与侵入量对比
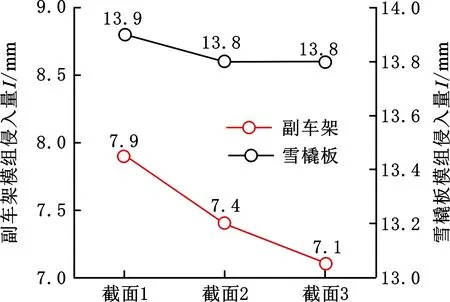
(b)不同位置的侵入量对比图12 三种截面的对比Fig.12 Comparison of three types sections
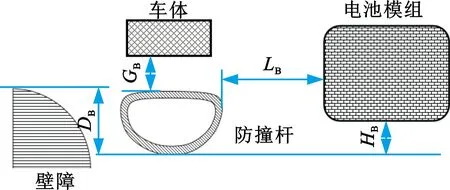
图13 布置参数评估模型Fig.13 Evaluation model for layout parameters
通过单因子法验证4种参数对模组侵入量的影响,共设计了A、B、C、D、F、E 5种状态,其中状态A为基础状态,每次单独更改一个参数的状态,如表2所示。

表2 布置参数取值
分析结果如图14所示,结果表明,HB、GB、DB对模组侵入量有明显的影响,随着距离的增加,模组侵入量呈现增大趋势,而LB对模组侵入量影响不明显。因此本文针对防护结构的优化,需要考虑在高度方向上的布置参数。

图14 布置参数对模组侵入量的影响Fig.14 Influence of layout parameters on the module intrusion

图15 刮底工况速度曲线Fig.15 Velocity curves of bottom-scraping condition
3.5 防护结构影响电池包侵入机理分析
基于前文的分析结果,统计了相应的整车速度曲线,如图15所示。速度曲线有两种趋势,分别选一个代表性曲线,趋势1以红线表示,趋势2以黑线表示,两者的速度曲线趋势不同,也代表着两种不同的模组侵入。趋势1的模组侵入量明显低于趋势2。通过研究可知:
(1)阶段1在10 ms左右时,趋势1的防护结构开始接触到壁障,速度立刻下降。由于壁障与副车架有部分重叠,趋势2速度逐步下降。趋势2的防护结构在50 ms开始接触壁障,降速效果有所增加。在阶段1最后时刻,速度基本一致。
(2)阶段2从62 ms左右开始,壁障接触到电池包框架,速度进一步下降。其中趋势1曲线下降不明显,而趋势2曲线有更加明显的下降。经观察碰撞过程,分析原因为在阶段1,壁障与防护结构相互作用,迫使汽车沿着与地面以大小为θ的角度行驶,如图16所示。趋势1产生角度大于趋势2,当壁障接触电池包框架时,趋势1的壁障与电池包框架Z向重叠量更小,因此降速相对较小。
(3)阶段3从90 ms开始,两种趋势虽然速度不同,但速度均基本保持不变,这是因为电池包结构与壁障不再产生明显碰撞,因此整车降速不明显,汽车继续向前行驶。由于趋势1的速度更高,能够更快速地掠过壁障。
综上可知,电池包刮底防护设计关键在于防护结构迫使汽车上抬θ角度后快速行驶掠过壁障,而不是依靠吸能降低对电池包的冲击。若完全依靠防护结构将汽车停止,首先会增加较大重量,带来制造成本增加,同时撞击会对车身结构造成不可避免的损害,也会导致维修成本增加。
4 电池包防护结构轻量化设计
4.1 变量定义
根据第3节的研究结果,综合考虑截面尺寸、布置位置、厚度三类参数,共定义10个变量:3个截面变量、1个高度布置变量和6个厚度变量,如图17所示。通过Morph方式,采用截面节点比例变动的方法,控制截面节点的位置实现对截面形状的控制。例如截面增大10 mm对应的截面变量值为1.0,则-1.0和2.0分别对应截面减小10 mm和增大20 mm。各个变量的初始值及取值范围见表3。
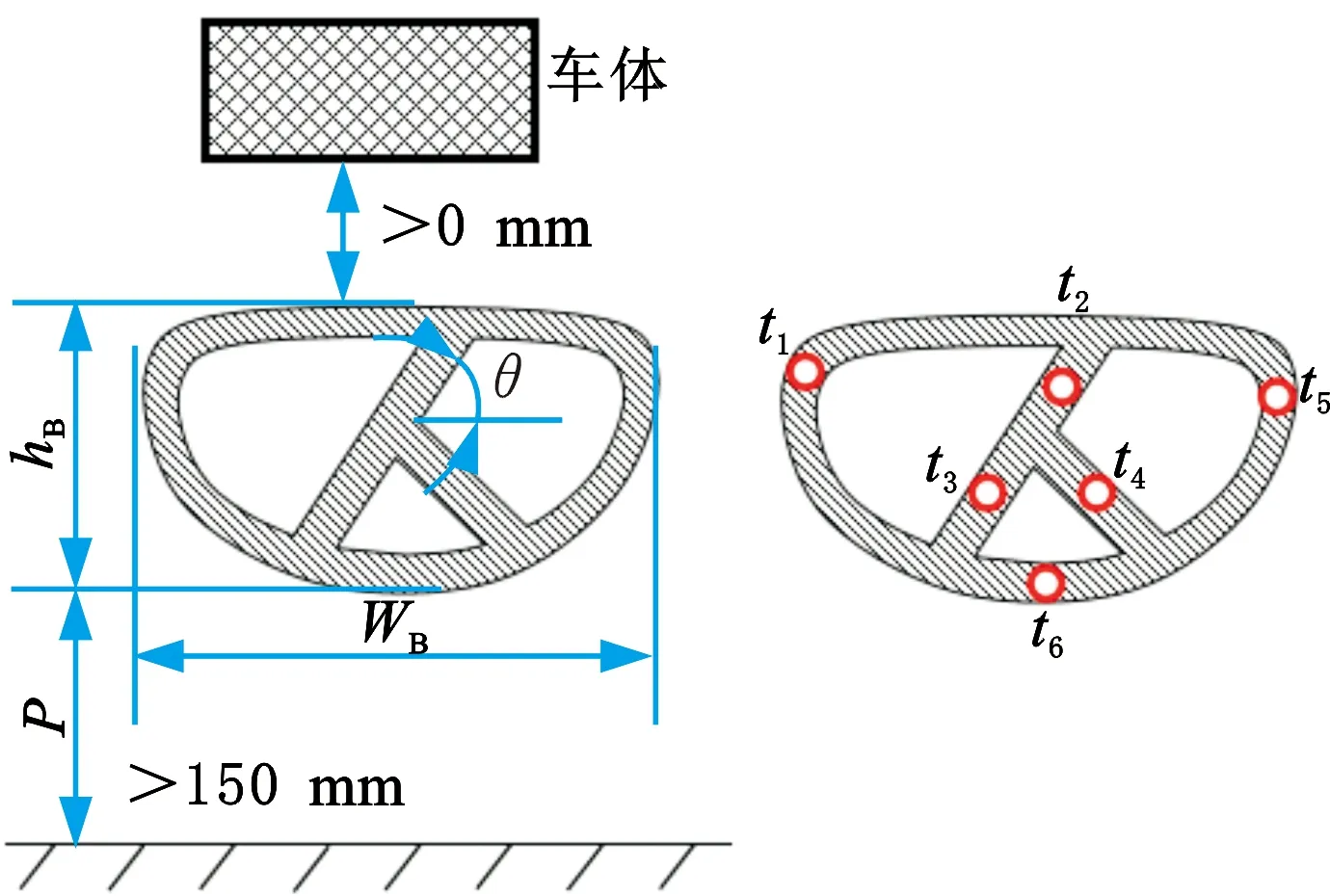
图17 变量定义Fig.17 Variable definition
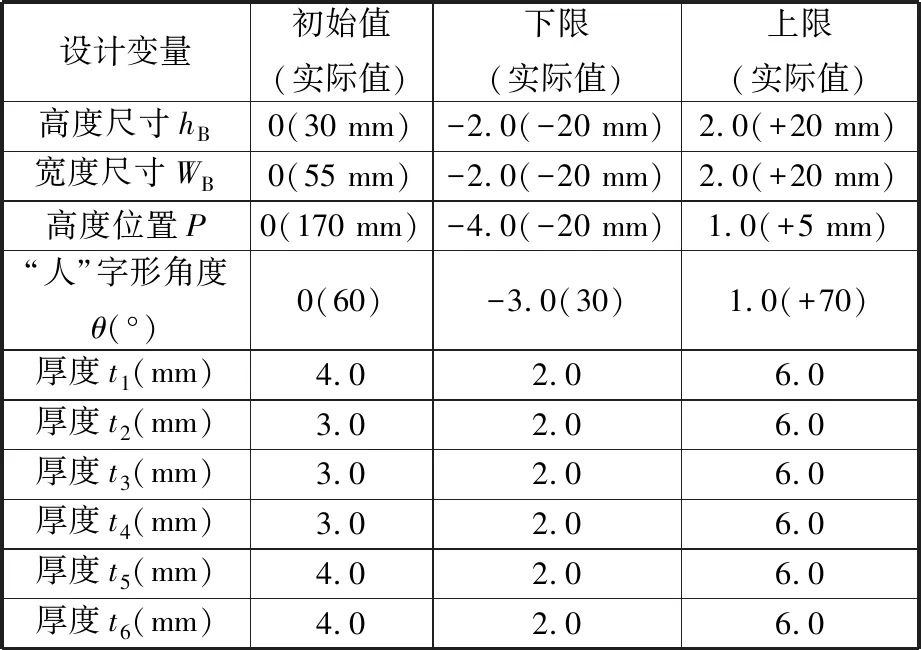
表3 变量参数
4.2 优化数学模型定义
防护结构的多目标优化问题可描述为:满足约束的前提下,要求电池模组侵入量最小,与此同时保证其质量最小。本文将10个设计变量作为约束,同时为保证截面变化过程中防护结构不与车体干涉(大于0 mm)、满足离地间隙(大于150 mm)要求,因此需要控制hB和P尺寸变量间的关系。将防护结构质量、电池模组侵入量作为设计目标,建立优化模型:
(1)
式中,x为第i个设计变量;xli、xui分别为xi的设计下限和上限;m为防护结构质量。
防护结构与车体之间的初始距离为10 mm,因此5hB+5P导致的结构位置的上升不应超过初始距离。防护结构的初始离地距离为170 mm,为了满足大于150 mm的要求,5hB+5P导致的结构位置下降不应超过20 mm。
4.3 混合近似模型
由于针对每一种组合进行仿真的工作量巨大,因此采用DOE方法对以上数据进行取样,尽量保证足够多的样本点以提高后续建立的近似模型的准确性。由于定义了变量约束,本文采用改进的可扩展晶格序列法取样,此方法相比拉丁超立方采样方法,采样点更均匀,可自动进行空间填充。样本点总数设定为73组,利用LS-Dyna对这73组数据进行碰撞仿真分析,得到每一组数据对应的侵入量性能指标。为避免单一近似模型带来的拟合精度问题,本文选择混合近似模型[17],基于RBF(径向基神经网络)和Kriging(克里金)方法,利用其中65组试验数据分别构建质量m、电池模组侵入量I与各变量之间的关系近似模型。剩余8组数据通过R2相关系数法作误差分析,计算表达式为
(2)

经分析可知,质量m与模组侵入量I的R2误差分别为0.946、0.958。近似模型的误差散点图见图18,可以看出,响应的预测值与样本点真实值吻合较好,即确定建立的近似模型符合后续优化的要求。

图18 近似模型误差散点图Fig.18 Error scatter plot of approximate model
4.4 基于多目标海洋捕食者算法的多目标优化
ZHANG等[18]基于海洋捕食者算法(Marine Predators Algorithm,MPA)[19]提出了多目标海洋捕食者算法MOMPA,通过使用CEC2019多模态/多目标优化基准函数验证了所提出的MOMPA的有效性和优越性,并利用汽车侧面碰撞问题验证了所提出算法的有效性,结果显示MOMPA具有稳定的性能和强大的鲁棒性。基本流程如下:
(1)初始化构建猎物矩阵,捕食者基于这个矩阵更新它们的位置。猎物矩阵为
(3)
式中,N为种群规模;D为每个维度的位置(问题的解的维度)
(2)更新存储迄今为止找到的Pareto最优解的存档,此存档用于存储非支配最优解,并包含迄今为止发现的一组非支配最优解决方案,它的容量大小通常是种群的一半。此存档始终从现有种群中收集解决方案,并通过将其与新生成的解决方案进行比较来更新存档。
(3)从存档中选择最合适的顶级捕食者。重新计算每个个体的新适应度值,并选择所有适应度值最佳的个体作为顶级捕食者,精英矩阵为
(4)
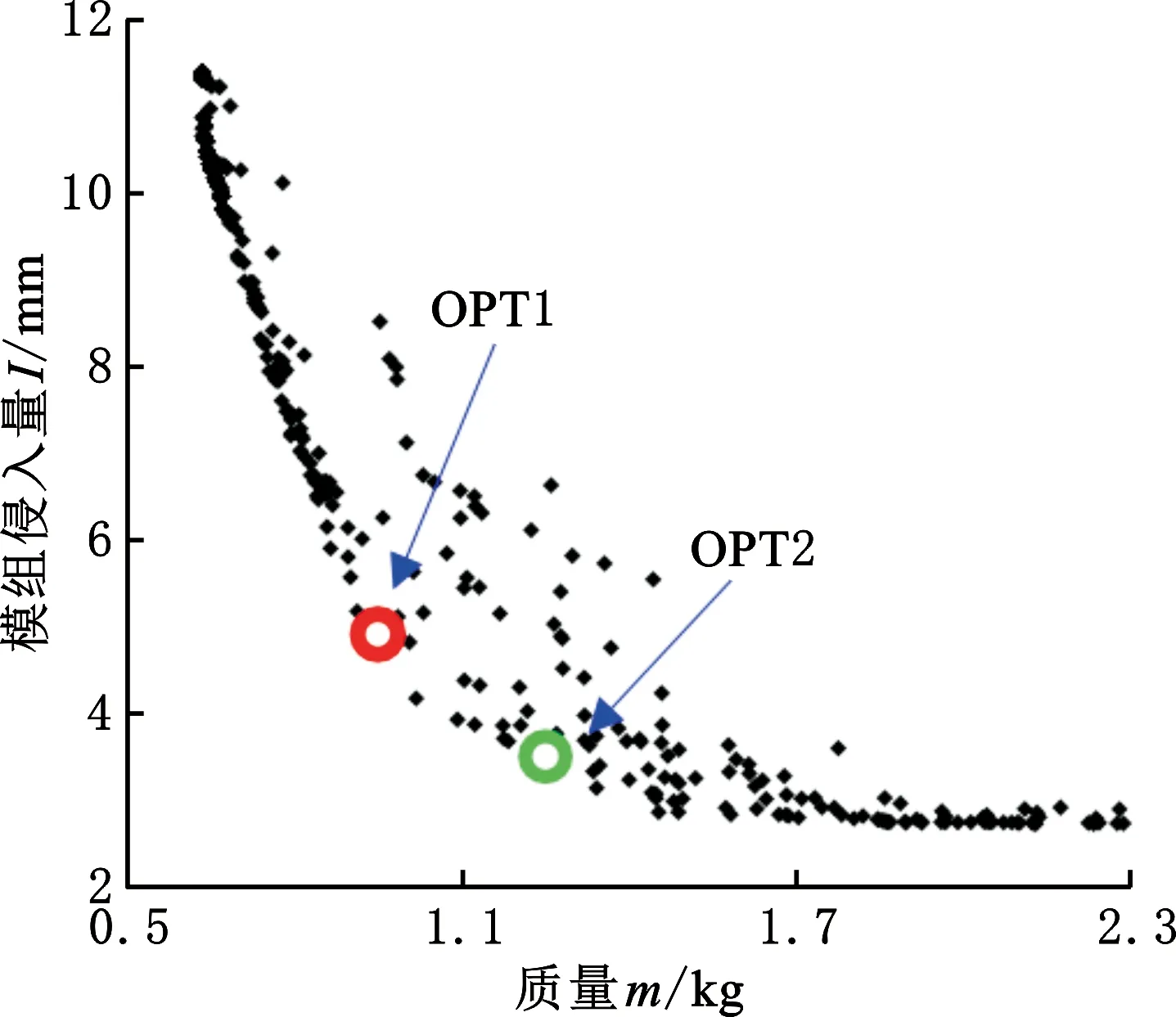
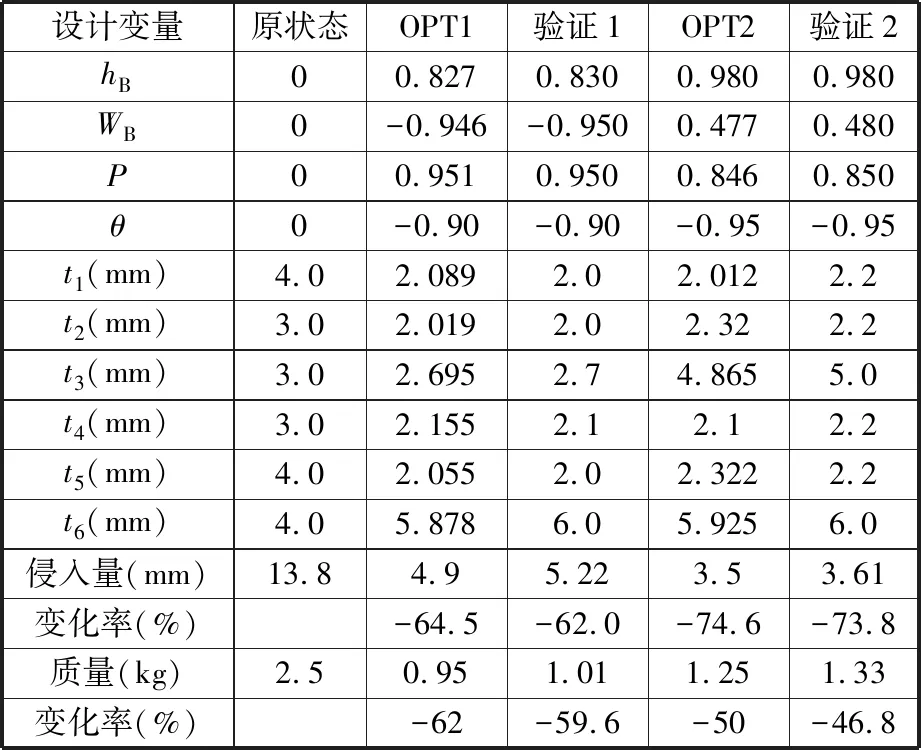
式中,X(1),X(2),…,X(m),…,X(k)表示使用精英选择方法选择的顶级捕食者,其中1 精英矩阵为每个捕食者提供最佳当前猎物位置。 (4)MOMPA通过三个阶段模拟海洋捕食者及其猎物的生物。 (5) 式中,RB为一个基于非正态分布的包含随机数的向量,表示布朗(Brownian)运动;Q为等于0.5 的常数;R为[0,1]之间的均匀的随机向量;g为当前迭代次数;gmax为最大迭代数;Si表示第i个捕食者下一步移动步长的向量。 (6) 式中,RL为基于莱维分布的随机数向量;CF为控制捕食者移动步长的自适应参数。 (7) 其中,RL与精英矩阵的乘积模拟了捕食者的莱维运动,并通过增加精英的步长,将捕食者的运动模拟为猎物位置的更新。 除了上述阶段之外,涡流的形成和鱼类聚集装置(fish aggregating devices,FADs)对捕食者也有影响,该阶段数学公式如下: XPreyi= (8) 其中,pf=0.2,为优化过程中受FADs影响的概率;r是从0到1范围内生成的随机数;U是一个包含0和1的二进制向量。如果r小于0.2,则U设置为0,如果r大于0.2,则U设置为1;XPreyr1和XPreyr2为猎物矩阵的随机索引。 为实现算法在求解域内的广泛搜索,设种群规模为 400,精英矩阵存档规模为200,FADs为0.2,Q为0.5,最大迭代步数为100,最终优化后Pareto前沿解如图19所示,设计空间具有合理的分布,包括Pareto前沿的多样性特征。本文分别从质量最优和性能最优两个角度选取了两个优化结果OPT1和OPT2。相比原钢制防护结构,OPT1实现了质量减小62%,电池模组侵入量降低至4.9 mm;OPT2实现了质量下降50%,电池模组侵入量降低至3.5 mm。 图19 Pareto前沿解Fig.19 Front solution of Pareto 为验证防护结构的优化效果,对最优解进行参数圆整,与优化前防护结构进行仿真对比。表4的验证结果表明,本文的铝合金防护结构通过拓扑优化和多目标优化,实现了重量及侵入量的降低:OPT1验证方案实现减重59.6%,侵入量降低62%,侵入量略微超标,但仍然可以接受;OPT2验证方案实现减重46.8%,侵入量降低73.8%。 表4 仿真结果验证 (1)本研究以电池包刮底防护结构为轻量化对象,定义了仿真分析工况及电池模组侵入量考察指标,建立了整车碰撞有限元模型,通过实车试验验证了整车有限元模型的准确性,并基于整车碰撞模型分别对钢制和铝制防护结构进行验证对比。结果表明两种结构的侵入量的基本相等,同时,雪橇板位置相较于防护结构安装在副车架位置效果更优。 (2)基于6063-T6铝合金设计防护结构,其材料性能通过三点静压试验进行了验证。通过拓扑优化,将铝合金防护结构截面设计为“人”字形,侵入量相比传统截面降低10%。模组侵入量与防护结构的垂直方向的安装位置有明显相关性,而与电池模组的纵向距离关联性不明显。 (3)构建了RBF和Kriging混合近似模型并用于拟合设计变量与响应之间的映射关系。基于建立的混合近似模型,联合MOMPA得到非支配Pareto解,并分别从质量最优和性能最优的两个角度,选取了两个优化结果。相较于原始设计,基于多目标优化方案验证,OPT1验证方案实现减重59.6%,侵入量降低62.0%;OPT2验证方案实现减重46.8%,侵入量降低73.8%,取得了较好的轻量化效果。
4.5 优化结果验证
5 结论
