纤维混凝土桥梁外表裂缝检测技术的仿真模型实验

李乔乔

(广东交科检测有限公司,广东 广州 510550)

目前,桥梁裂缝的检测识别主要是基于机器学习的方法,如针对传统人工检测方法存在成本高和危险性高的问题,结合无人机技术与机器学习,提出一种基于Mask R-CNN的桥梁结构裂缝智能识别方法[1]。以卷积神经网络为核心算法,通过采用无人机技术拍摄的桥梁结构图像构建数据库,提出一种混凝土桥梁裂缝识别与定位方法[2]。提出一种基于加入残差块的桥梁裂缝像素级检测算法,实现了桥梁裂缝的快速识别[3]。通过上述研究可以发现,基于机器学习的检测识别方法在桥梁裂缝检测中取得了良好的检测效果,但有学者认为,现有的各种基于机器学习的检测方法对桥梁纤维混凝土裂缝的检测准确率有待进一步提高[4]。为解决该问题,以桥梁表面常用的纤维混凝土作为研究对象,提出一种基于改进VGG16的桥梁纤维混凝土裂缝检测方法。

1 基本算法

1.1 VGG16模型

VGG16模型是一种常用于目标检测的高效识别算法模型,基本网络结构如图1所示[5]。该模型输入图像大小为224×224×3,通过2个卷积层进行卷积与矩阵填充,可得到224×224×1的矩阵。由于第1层包括64个卷积核,因此可得到224×224×64的矩阵。然后通过卷积核大小为2×2×64,步长为2的5层池化层,可得到7×7×512的矩阵[6]。最后,进入具有3层结构的全连接层,再进行Softmax分类,即可实现对样本的分类处理,得到当前样本属于不同种类的概率分布。

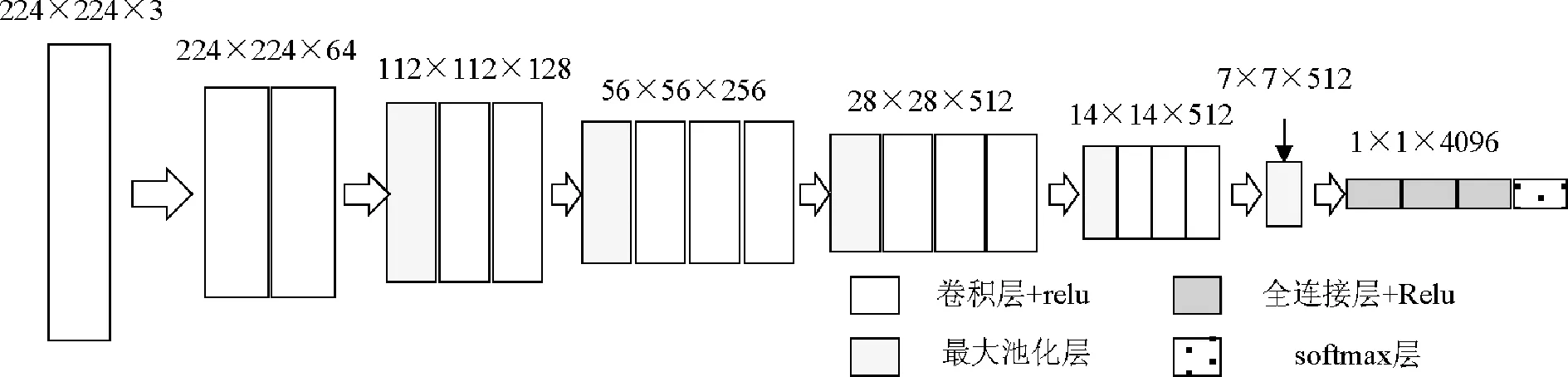
图1 VGG16模型结构示意图

1.2 VGG16模型改进

研究对VGG16模型的改进主要集中在3个方面:(1)将3层卷积层和5层池化层修改为6层包括卷积层和池化层的大卷积层,对输入图像进行卷积运算加深网络,以适当提高模型的识别精度;(2)对卷积核和池化窗口进行改进,将卷积核大小设置为3×3,池化窗口尺寸设置为2×2,以增加网络的感受野;(3)同时降低模型的参数量,进而提高模型的运行效率[7]。

通过上述改进,得到改进后VGG16模型结构,具体如图2所示,由输入层、输出层、大卷积层、全连接层、softmax分类层组成。其中,卷积核的大小均为3×3,步长为1;池化窗口大小为2×2,步长为2。输入224×224×3的图像通过大卷积层卷积和池化后,可得到3×3×512的矩阵输入3层全连接层,然后通过Softmax分类与输出层输出,即可对图像进行分类识别。

图2 改进VGG16模型结构示意图

改进后的VGG16模型相较于标准VGG16模型,具有更快的训练速率和更高的识别精度。因此,研究采用改进的VGG16模型对桥梁表面纤维混凝土裂缝进行检测,以实现高速率高精度的裂缝识别。

2 基于改进VGG16的桥梁表面纤维混凝土裂缝检测模型

2.1 模型训练

2.1.1激活函数确定

激活函数是影响改进VGG16模型训练的关键参数。常见的激活函数包括Sigmoid函数、Relu函数和Tanh函数等。相较于其他激活函数,Relu函数由于采用随机梯度下降法进行训练,解决了梯度消失的问题,可提高模型的稀疏表达能力。因此,研究选用Relu函数作为改进VGG16模型的激活函数,其数学表达式[8]:

f(x)=max(x,0)

(1)

2.1.2损失函数确定

损失函数是解决模型过拟合的参数。神经网络常用的损失函数包括L1正则化损失和L2正则化损失两种。其中,相较于L1正则化不可导,L2具有可求偏导的特性更适用于改进VGG16模型。因此,研究改进VGG16模型选用L2正则化损失,其数学表达式[9]:

(2)

式中:R(w)为模型复杂函数,表示模型复杂程度;wi为参数i的权重。

2.1.3反向传播算法确定

常用反向传播算法包括梯度下降法和随机梯度下降法等。虽然随机梯度下降法训练时间更短,但若随机性太强,可能达不到理想寻优结果[10]。因此,为实现快速训练并取得寻优结果,研究对部分数据采用梯度下降法进行反向传播,对剩余部分数据采用随机梯度法进行反向传播。

2.1.4学习率确定

学习率即神经网络每次训练时参数移动的幅度。为确定学习率,研究采用指数衰减法先以较大的学习率确定范围,然后再不断减小学习率确定其最佳值。指数衰减法的数学描述[11]:

η=η0×λ(α/β)

(3)

式中:η、η0分别为指数衰减学习率和初始学习率;λ为学习率衰减系数;α/β为总样本数与训练轮次的比值。

2.2 模型检测流程

(1)收集整理相关桥梁纤维混凝土裂缝的图像。考虑到图像可能存在阴影、扭曲等问题,需对图像进行预处理;(2)将预处理后的桥梁纤维混凝土裂缝图像输入训练完成的改进VGG16模型中进行学习与训练;(3)将改进VGG16模型的输出作为检测识别结果,即实现了桥梁纤维混凝土裂缝的检测。

3 仿真实验

3.1 实验环境搭建

实验基于TensorFlow深度学习框架和Python语言搭建并训练所提改进VGG16模型,使用Visual Studio Code编译器,在Windows10操作系统上运行。系统配置Intel(R)Xeon(R)Gold6152 CPU,NVIDIA Tesla P40显卡,24 GB显存,256 GB内存。

3.2 数据来源及预处理

本次实验数据来自2个部分:一是自主拍摄的桥梁纤维混凝土裂缝图像;二是网络搜寻的桥梁纤维混凝土裂缝图像。针对网络搜寻的图像,考虑到图像采集过程中可能存在变形、模糊、亮度不均匀等问题,试验前对图像进行了预处理。考虑到图像数量对于机器学习的神经网络模型相对较少,实验对图像进行裁剪、缩放、翻转等进行增强处理。共获取用于桥梁纤维表面混凝土裂缝检测的图像共5 000张。

3.3 评价指标

本次实验选用准确率(CCR)作为评估所提改进VGG16模型性能的指标,其计算方法[12]:

(4)

式中:T1、T2分别为分类正确样本数及样本总数。

3.4 超参数设置

超参数是影响模型精度的重要参数,包括初始学习率、批大小、优化器、迭代次数[13-15]。为获取最佳模型超参数,研究通过控制变量法试验进行确定。图3所示为批大小、优化器、迭代次数3个超参数一致条件下,不同初始学习率所提改进VGG16模型的准确率。

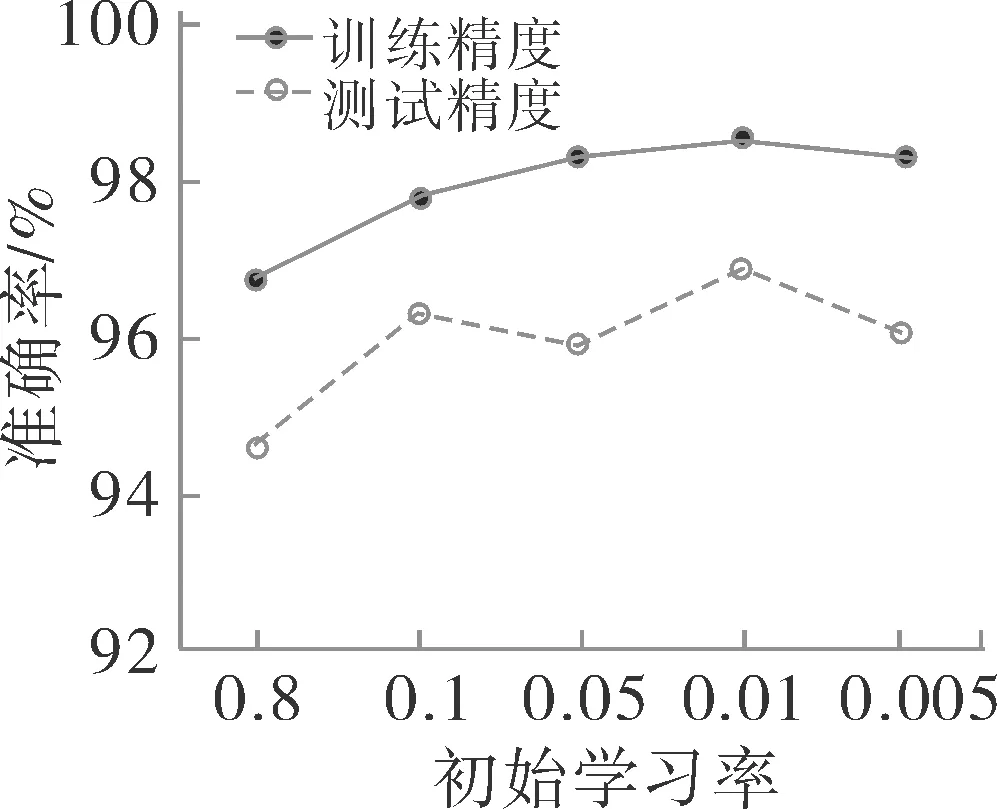
图3 不同初始学习率条件下改进VGG16模型的准确率

由图3可知,当初始学习率为0.01时,所提模型的训练准确率和测试准确率最高。因此,实验设置所提改进VGG16模型的初始学习率为0.01。

图4为初始学习率为0.01时,相同优化器和迭代次数条件下,不同批大小时所提改进VGG16模型的准确率。

图4 不同批大小条件下改进VGG16模型的准确率

由图4可知,当批大小为32时,所提模型的训练准确率和测试准确率最高。因此,本次实验设置所提模型的批大小为32。

图5为初始学习率为0.01、批大小为32,迭代次数相同而优化器不同条件下,所提改进VGG16模型的准确率。

图5 不同优化器条件下改进VGG16模型的准确率

由图5可知,采用梯度下降法作为反向传播优化器时,模型的训练准确率和测试准确率均高于与Adam作为优化器。因此,本次实验设置所提模型的优化期为梯度下降法。

图6为初始学习率为0.01、批大小为32、优化器为梯度下降法时,所提改进VGG16模型在不同迭代次数下的准确率。

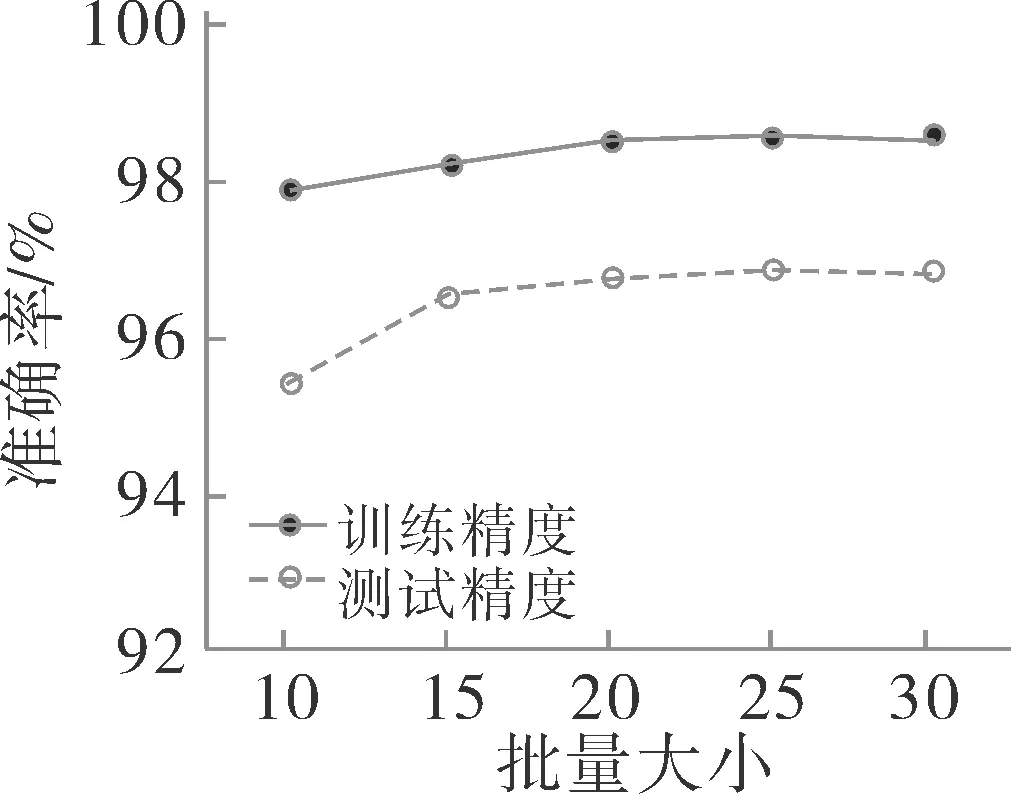
图6 不同迭代次数下改进VGG16模型的准确率

由图6可知,当迭代次数为25时,所提模型的训练准确率和测试准确率最高。因此,本次实验设置所提模型的迭代次数为25。

4 结果与分析

4.1 算法验证

为验证所提改进VGG16模型的有效性,基于上述超参数,实验对比了改进前后模型的训练准确率和测试准确率,结果如图7所示。

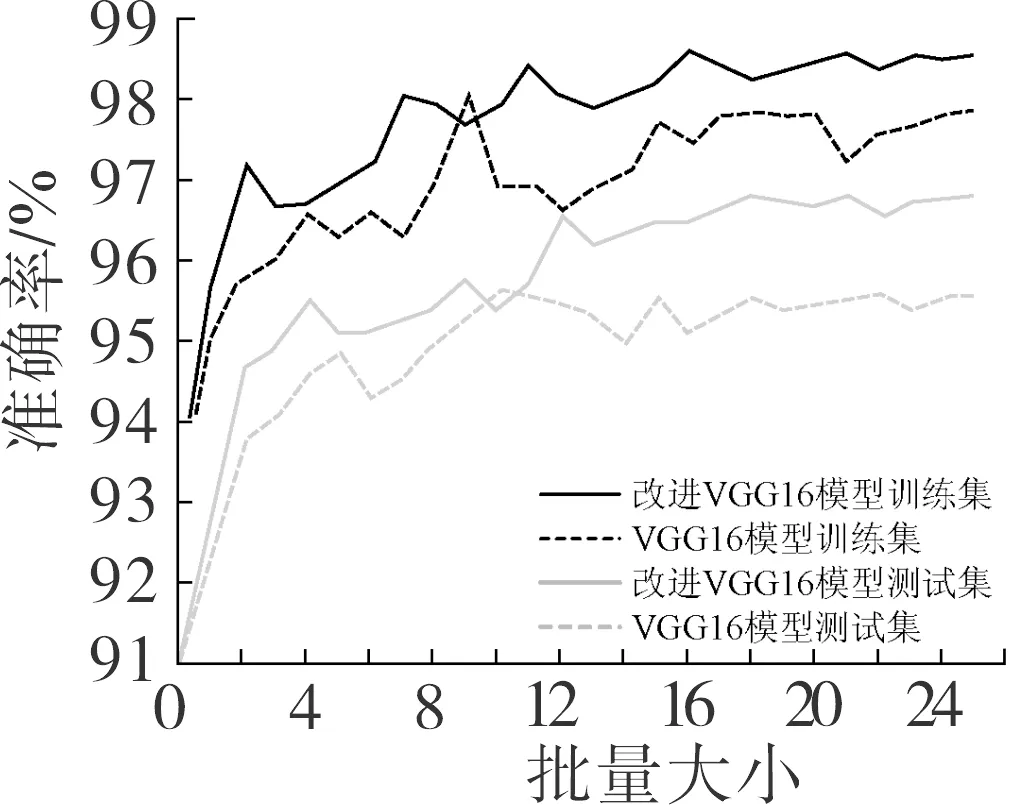
图7 VGG16模型改进前后准确率对比

由图7可知,相较于改进前VGG16模型,所提模型的训练准确率和测试准确率均得到了不同程度提升,分别达到98.65%和97.89%。由此说明,本研究对VGG16模型改进有效。

4.2 算法应用效果对比

图8为图片规范采集条件下,所提模型与对比模型对存在腐蚀的桥梁纤维混凝土裂缝的识别结果。

(a)原始图像

由图8可知,所提改进VGG16模型可有效识别分类桥梁纤维混凝土裂缝;而Canny模型在腐蚀产物的干扰下不能提供裂缝的有效信息,不能对裂缝进行有效识别。Sobel模型的识别结果存在较大的干扰,可提供部分裂缝信息,识别能力有限。改进VGG16模型在桥梁纤维混凝土裂缝检测识别中,相较于常规检测识别方法,具有一定的优越性。

5 结语

综上所述,所提基于机器学习的桥梁纤维混凝土裂缝检测方法,通过减少VGG16部分卷积核和全连接层通道数量,并在卷积层和全连接层后添加Relu函数,同时引入Dropout,提高模型的运行速率和识别精度,可实现高速率高精度的桥梁纤维混凝土裂缝检测识别。相较于标准VGG16模型以及常规检测识别模型Canny模型和Sobel模型,所提改进VGG16模型可实现对存在阴影、扭曲等问题的桥梁纤维混凝土裂缝图像的检测识别,且具有更好的识别准确率,训练准确率和测试准确率分别达到98.65%和97.89%,具有一定的实际应用价值。