一种改进的增量型随机权神经网络及应用∗
2023-10-20谢林柏
刘 伟 谢林柏 彭 力
(江南大学物联网工程学院 无锡 214122)
1 引言
火灾探测是一个社会热点问题,关系到每个人的生命和财产安全。传统的传感器火焰检测方法存在抗干扰能力差,响应时间长和准确性低等问题。随着计算机技术的发展,结合计算机视觉和数字图像处理的火灾检测算法得到了广泛研究。提取火焰特征,使用模式识别算法检测火焰是图像型火焰检测的一类主流方法。火焰检测领域中的模式识别算法包括支持向量机、神经网络、贝叶斯分类器、决策树以及马尔可夫模型等[1]。单隐藏层前馈神经网络(SLFN)由于结构简单,且能够以任意精度逼近复杂非线性连续函数,被广泛运用于分类识别问题。但是,传统的SLFN 在训练过程中基于梯度优化网络参数,迭代时容易陷入局部最优,且耗时较长[2]。为了缓解上述问题,Pao[3]提出了一种使用不同训练机制的网络,即随机权神经网络(Random Vector Functional Link,RVFL)。RVFL 最大特点是网络中的输入权值和隐藏层(也称为增强层)偏差在给定范围内随机分配,并在整个训练过程中保持固定,然后采用最小二乘法对输出权值进行计算。整个训练过程不需要迭代,保持快速学习的同时拥有良好的泛化能力。隐藏层节点数是RVFL 中唯一需要预定义的参数,它在确定学习性能以及网络计算效率方面起着至关重要的作用[4]。设置过少的隐藏层节点会因为拟合不充分而导致训练误差过大。设置过多的隐藏单元又会因为过拟合而导致训练误差较小,但降低训练模型的泛化能力。
针对以上问题,Huang[5]提出了一种增量型RVFL(I-RVFL)算法,并将其命名为增量型极限学习机。在添加新的隐藏节点前,所有现有隐藏节点的输入和输出参数固定不变,只需要计算新添加的隐藏节点的输出权值。I-RVFL不仅具有良好的泛化性能,也在一定程度上避免了“过拟合”问题[6]。
虽然增量型RVFL 可以获得极快的速度和较好的泛化性能,但是输入权值和隐藏层偏差是从固定范围随机生成,可能会导致模型不稳定,降低模型的学习效率[7]。近年来有许多方法被提出用于指导RVFL参数的选择,如激活函数的选择[8],隐藏层参数的随机范围选择[9]等,但是这些方法都是根据试验结果所得出的经验性方法。因此,在参数随机配置时,需要约束机制指导参数的选择以提高建模的效率和稳定性。
针对上述问题,本文提出一种改进的增量型RVFL 网络,利用指数加权平均算法优化随机参数以限制随机配置时产生的离群值;同时,将凸函数的下降梯度比运用到网络的误差序列中加快模型的收敛速度。最后,将改进的网络应用到火焰识别中,对采集的样本进行训练和分类。
2 增量型随机权神经网络
给定输入X={x1,x2,…,xN},xi∊Rd和标签值T={t1,t2,…,tN},ti∊Rm,当网络中已经构建L个隐藏节点时,可以表示为
式中,HL是输入和隐藏节点输出的连接矩阵,Y是模型的预测值。HL可以表示为
式中,xi=[xi1,…,xid]T表示第i个训练样本;ωi=[ωi1,…,ωiL]T和bi∊R分别为输入层到第i个隐藏层节点的输入权值和偏差;g(∙)为隐藏层的激活函数。βi=[βi1,…,βim]T表示第i个隐藏层节点的输出权值。
根据RVFL 学习算法[10],网络的输出权值β通过最小二乘解获得:
式中,H†是隐藏层输出矩阵H的Moore-Penrose广义逆。
当网络已经构建L个节点时,目标函数可以表示为
网络的误差:eL=f-fL=[eL,1,…,eL,m]。假设网络的最大隐藏节点数Lmax,预设的容忍误差为ϵ,当L>Lmax或者‖eL‖≤ϵ时,整个网络训练结束;否则,继续添加第L+1个节点。
3 算法改进
3.1 指数加权平均算法优化参数
指数加权平均算法是一种有效减少误差的统计学方法。该方法根据权重因子对历史数据和当前数据按照比例分配来稳定序列,平均输入流中的数据,逐渐降低对较早数据点的加权程度,平滑数据中的随机波动[11]。增量型网络通过逐个增加节点构建而来,可以将整个迭代过程视为一个具有历史数据的时间序列。计算指数加权平均值:
式中,VL是生成第L节点时的平均权值或偏差,θL是生成第L个节点时随机分配的权值或偏差,α是权重因子。α决定了各个神经元参数的权重。α的值越大,表明此次迭代的权值与偏差参考之前节点分配的权值与偏差的程度更多,平稳性更强。利用指数加权平均方式限制参数随机配置时产生的异常值,从而降低异常值对建模的影响,使整个模型训练过程更平稳有效。
3.2 凸函数优化误差序列
如图1 所示的两条单调递减曲线,其中函数y1(t)和y2(t)分别为凹函数和凸函数,显然y2(t)的下降速度快于y1(t)。考虑t1,t2和t3具有相等间隔,定义梯度比为
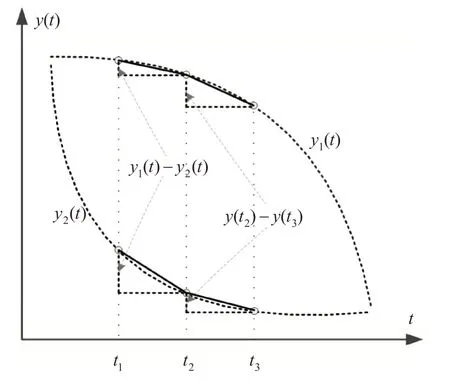
图1 凸/凹函数下降曲线
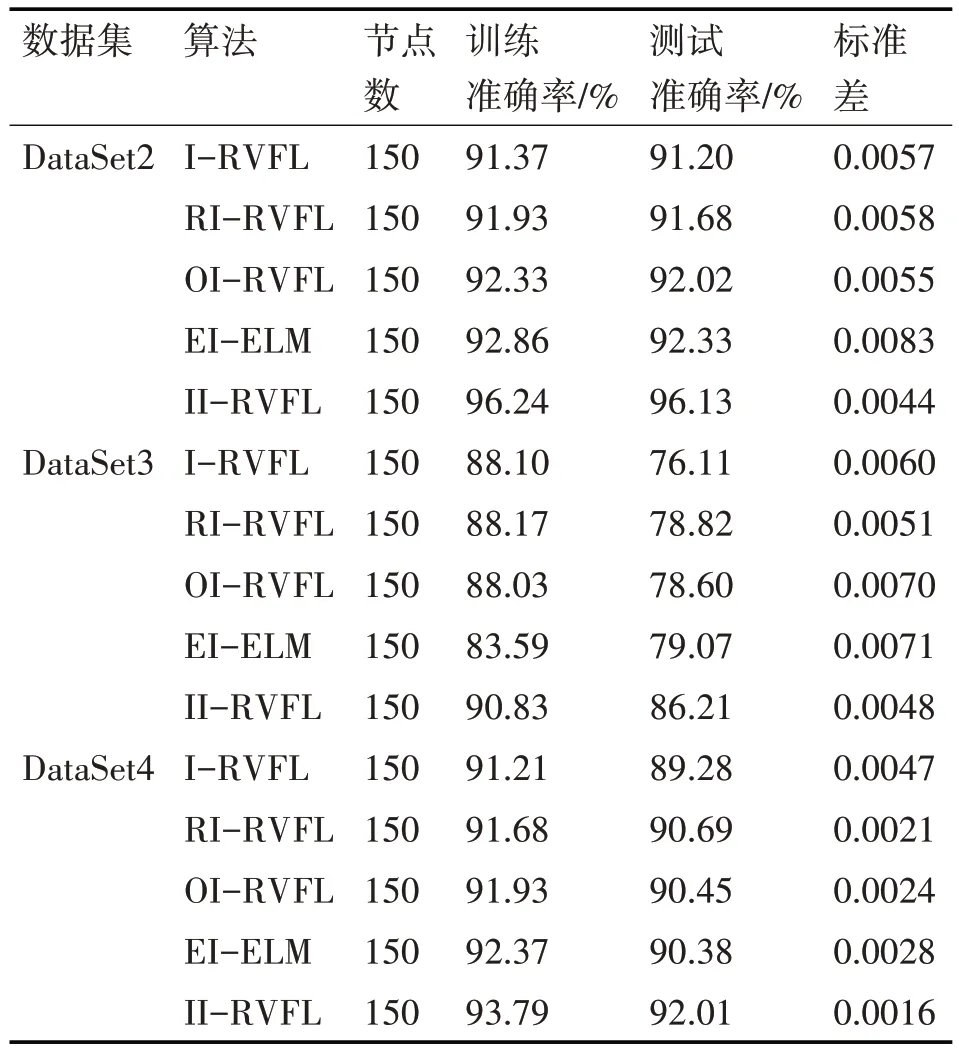
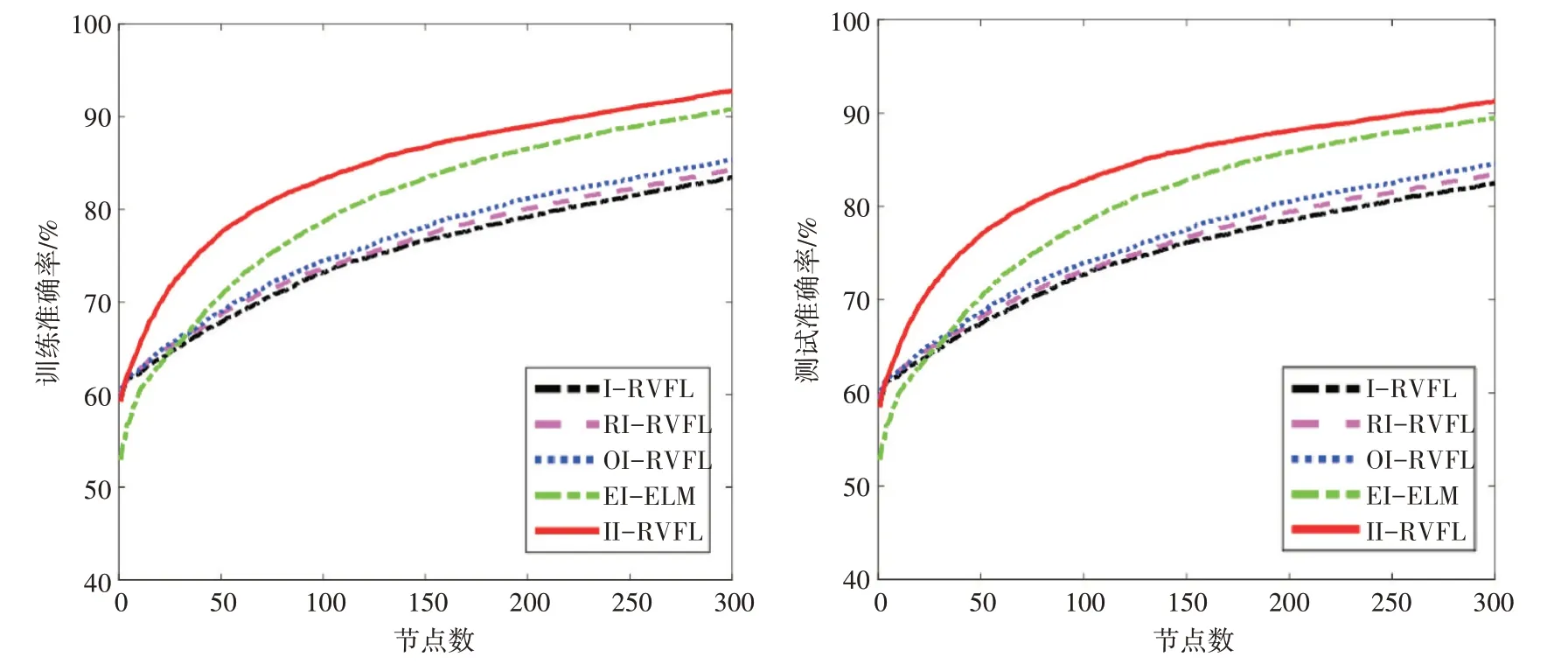
i=1,2 。根据凸函数的定义,对于t1 给 定 输 入X={x1,x2,…,xN},xi∊Rd和 标 签T={t1,t2,…,tN},ti∊Rm,构建第L个节点时,拟合误差eL-1=f-fL-1=[eL-1,1,…,eL-1,m] 。将上述函数的梯度比应用于误差序列,得到: 其中,gL是隐藏神经元的激活函数。将式(6)视为βL,q的方程,对其进行求导求极值: 将式(7)带入式(6),得: 因为0<λL,q≤1,因此: eL-1(X)=[eL-1,1,…,eL-1,m(X)]T,且eL-1,q(X)= 其 中,∆L=Σmq=1∆L,q,q=1,…,m。误 差 矩 阵 为[eL-1,q(x1),…,eL-1,q(xN)],q=1,2,…,m。 hL(X)=[gL(ωTLx1+bL),…,gL(ωTL xN+bL)]T表 示的是输入xi在第L个节点的激活函数值。 根据文献[12],将式(9)转化为如下形式: 式(5)~式(10)建立了误差序列之间的联系使得网络输入权值ω和偏差b不再是完全随机分配。更新的ω和b必须满足式(10)的∆L,q,且对于q=1,2,…,m都有∆L,q>0,通过这样一种约束关系,提升建模稳定性,加快模型训练的收敛速度。 指数加权平均算法的权重因子对于参数训练很重要,合适的权重因子可以提升整个建模过程的稳定性。权重因子过小,表明参考之前数据的比例较少,在随机产生离群值时,无法降低离群值的权重。权重因子过大,每次的输入权值与偏差值较为接近,在计算过程中浪费计算资源。本文选取集合{0.4,0.5,0.6,0.7} 的数作为权重因子动态调整的范围,并引入增强型增量网络[20]的训练方式,分配候选节点通过计算后筛选优质节点,进一步提升隐藏层神经元的质量。值得注意的是‖eL-2,q‖2在L=1 时并不存在,本文在增加第一个节点时,直接使用增强型网络节点的训练方式计算获得模型的训练误差e1。后续节点添加步骤的具体伪代码如下: 输 入 :数 据X={x1,x2,…,xN},xi∊Rd,标 签T={t1,t2,…,tN},ti∊Rm;输出:输出权值βL 1.初始化:初始误差矩阵e0=[t1,t2,…,tN]T,e1,节点数L=2,最大隐藏节点数Lmax网络的容忍误差ϵ,候选节点数M,参数的随机分配范围[-γ,γ]。 2.WhileL≤Lmaxand‖eL‖>ϵ 3.在区间[-γ,γ]内随机分配M个候选节点的权值与偏差 4.根据式(3)利用权重因子序列计算候选节点的权值与偏差 6.If min{∆L,1,∆L,2,…,∆L,m}≥0 ,保 存∆L=及其对应的(ω'(i),b(' i))。 7.Else返回步骤3。 8.搜寻满足,保存对应的,更新网络的ωL,bL。 9.根据X,ωL,bL计算输入和隐藏层节点输出的连接矩阵HL。 10.根据HL通过式(2)计算输出权值βL。 11.计算本次搜索后的误差eL=eL-1-βLHL,更新L=L+1。返回步骤2。 12.End While 现有图像型检测算法大多针对已经形成火灾的火焰进行分析与识别,对于未形成火灾的早期火焰检测能力有限[13]。普通相机也很难透过阻挡镜头的障碍物来检测,降低了探测器的监测能力。当图像中存在与火焰相似的背景时,会导致误报率上升。使用红外摄像机采集火焰数据可以有效地解决上述问题。红外热成像技术利用物体辐射出的波长,将被测物体的热量信息通过图像形式可视化展现,不受可见光和遮蔽物的影响,能够直接反映火焰燃烧的本质。红外火焰图像在燃烧阶段会表现出很多静态特征与动态特征。本文选取圆形度[14]与尖角数[15]作为静态特征,选取面积变化率[16]、相对稳定性[17]和边缘抖动性[17]作为动态特征。 面积、Hu 矩变化以及质心点的移动情况是动态特征,而模式识别算法处理的是静态数据。对于动态特征,主要利用其波动性[17]。本文以10 帧为间隔计算动态特征值的方差,将动态特征转化为静态数据。方差的计算公式为 式中,s2表示动态特征值的方差,m为间隔帧数,Xi表示当前帧的特征值,表示间隔帧数中特征值的平均值。 本节使用四个UCI 机器学习库的分类数据集来进行仿真实验。数据集的属性信息如表1所示。 表1 数据集属性信息 为方便描述,将改进的算法表示为II-RVFL。I-RVFL,RI-RVFL[18],OI-RVFL[6],EI-ELM[12]和II-RVFL 在DataSet1 上进行训练和测试的分类性能如图2 所示。从图中可以看出经过候选节点筛选和参数配置优化后的算法相对于其他算法能够保持良好的收敛速度以及泛化能力。从图中还可以看出,II-RVFL 在200 节点时的分类精度甚至高于I-RVFL、OI-RVFL、RI-RVFL 在300 节点的分类精度。表2 中数据集DataSet2-4 的结果也表现出II-RVFL在分类任务上的优越性,而且50次实验结果的标准差最小,表明在经过指数加权平均约束后的算法体现出更好的稳定性,最终分类精度的变化幅度最小且均值最高。尤其对DataSet3,在训练集精度相差不大的情况下,测试集的精度相对其他算法高出7 个~10 个百分点,表明了优化后算法的分类性能更好。 表2 DataSet2-4上的训练和测试的分类准确性 图2 各算法300节点分类性能:平均训练准确率和平均测试准确率 本节通过采集的红外火焰数据集来验证所改进算法的有效性。所采集的总样本数为1012,其中测试集样本个数为760,测试集样本个数为252。类似地,每个算法做50 次实验,选取50 次实验的平均值作为最终结果。图3 为各算法在红外火焰数据集上的分类结果,可以看出无论是训练集还是测试集,改进的算法II-RVFL在火焰数据集上同样表现出优异的分类性能。从表3 可知,相较于其他算法,II-RVFL 在20 个节点时,火焰识别精度已经达到98%以上。 表3 各算法检测的火焰准确率 图3 各算法的火焰数据集分类性能:平均训练准确率和平均测试准确率 另选200 组数据,通过训练好的参数进一步验证改进后的算法对火焰识别的有效性。为了能够清晰地显示火焰判别效果,将有火源的标签样本置为-1,没有火源的标签置为1。检测结果如图4 所示,其中横坐标代表样本序列,纵坐标代表输出的估计值。将估计值大于零的点判别为无火焰,将估计值小于零的点判别为有火焰。通过真实值与估计值的误差大小可以更直观地显示II-RVFL 算法识别的准确性,仅有少数点的估计值与真实值之间的误差较大,但都是处于误差容许范围内,无错报现象,实现了火焰识别的高准确率预报。 图4 II-RVFL算法的火焰检测结果 本文针对I-RVFL网络的输入权值与偏差随机分配导致的模型不稳定问题,提出使用指数加权算法来优化随机配置时产生的离群值,并将凸函数的下降梯度比应用于网络的误差序列中来优化建模过程。通过这两种方法改善了网络参数随机配置中存在的问题。最后,使用UCI数据集和在红外火焰识别上的应用来进一步验证算法的有效性。实验结果表明,优化后的算法稳定性更高,泛化性能更好,火焰识别的准确率高。3.3 算法步骤
4 火焰的特征提取与预处理
4.1 特征提取
4.2 预处理
5 实验结果与分析
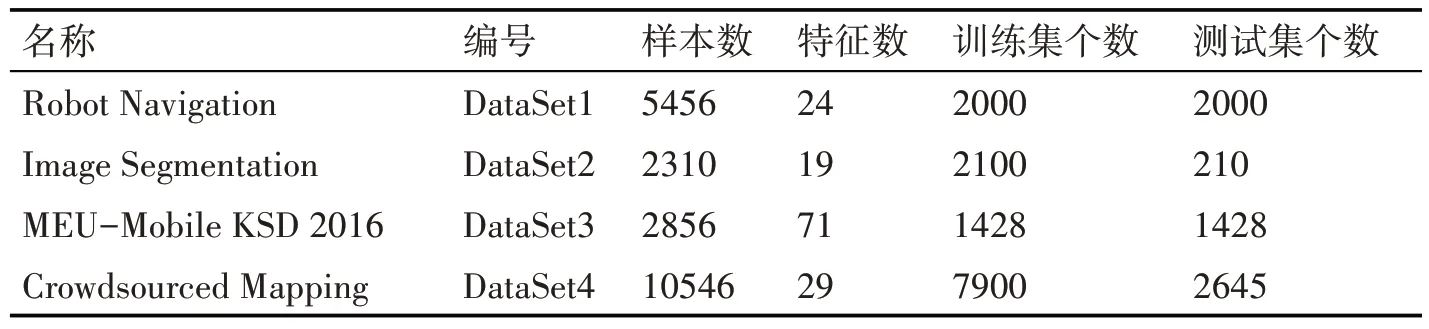
5.1 UCI数据集验证
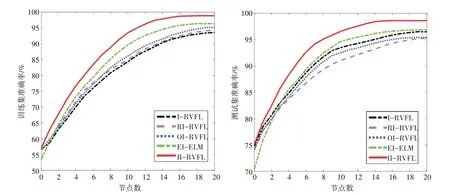
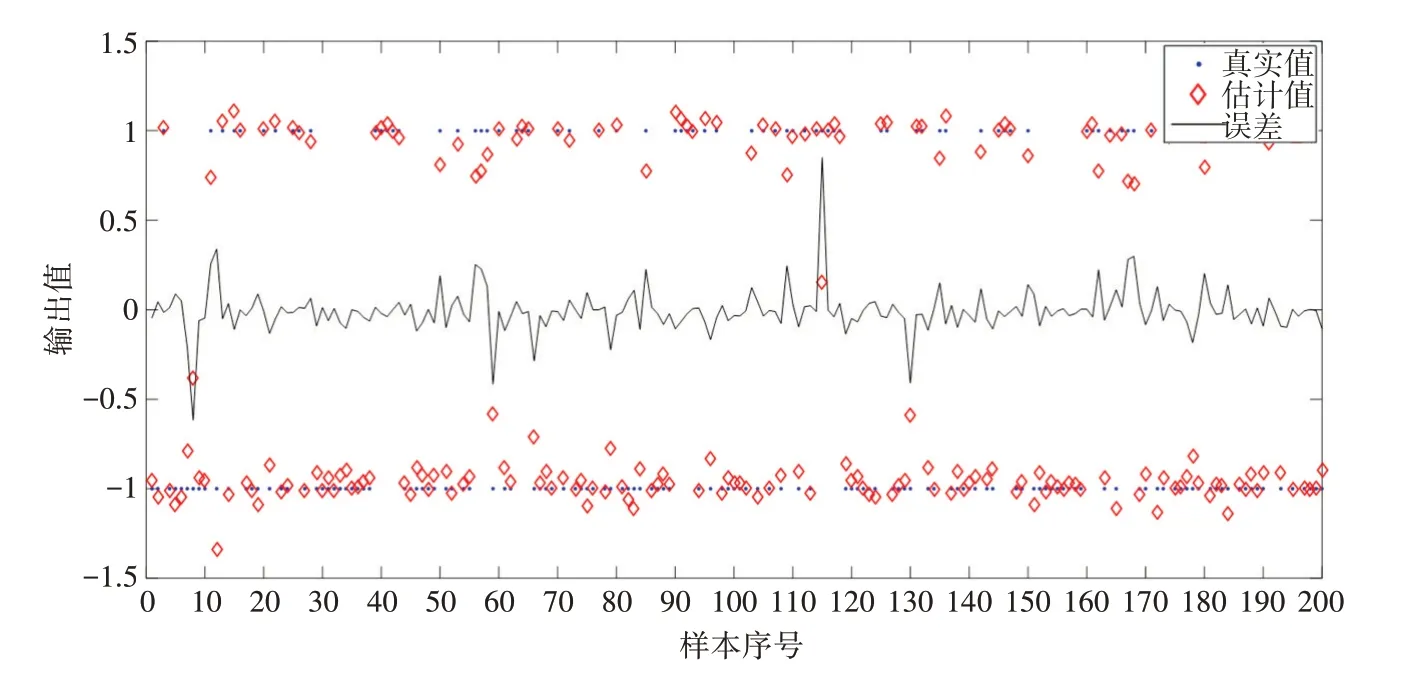
5.2 红外火焰识别中的应用
6 结语
