基于NSGA2 的参数自确定数据补全模型∗
2023-10-20赵亚茹崔志华徐玉斌
刘 浩 赵亚茹 崔志华 徐玉斌
(太原科技大学计算机科学与技术学院 太原 030024)
1 引言
在日常工作生活中,因为一些不可抗拒的因素,存储、传输过程中的数据经常遭遇元素信息丢失的困境,这严重影响了大数据时代下人类的正常工作生活。近些年,伴随着张量技术[1~2]的飞速发展,大量基于分解的数据补全模型[3~4]被提出用于缺失元素补全问题的研究。在二阶张量(矩阵)型数据的补全问题研究中,破损的数据矩阵被分解为两个因子矩阵[5]。这两个因子矩阵通过迭代计算方式求得,且它们的乘积即为破损数据矩阵补全完整后的结果。在文献[6]中,研究人员将Canonical Polyadic 分解(CP 分解)转化成一个加权最小二乘问题对破损数据进行补全,因此该方法也被称之为CP 加权优化。针对同一个张量数据,基于不同张量分解方法构建的数据补全模型性能存在着一定差异。这是因为不同的张量分解方法拥有着各自的特征属性,所适用的张量数据类型也不尽相同。基于此,研究人员基于不同张量分解方法构建了多种数据补全模型,并对其进行深入研究,诸如:Tucker 分解数据补全模型[7]、Tensor Train 分解数据补全模型[8]以及Tensor Tree 分解数据补全模型[9]等。在文献[10]中,作者提出了一种非迭代分解的张量分解技术,并与主成分分析技术(Principal Component Analysis,PCA)相结合,一起用于针对高光谱图张量数据的研究与应用中,并取得了不错的效果。在文献[11]中,针对Tensor Train 分解,一种新的迭代更新方式被提出以增强对大规模张量数据的数学可处理性和可扩展能力。在文献[12]中,基于Tucker 分解的数据补全模型通过随机投影的方式完成Tucker 分解过程,以补全破损缺失的数据。然而,基于分解的数据补全模型性能直接受到了模型输入参数低秩与最大迭代次数的影响。以上文献中所进行的改进虽然提高了分解技术的性能,但对于分解模型输入参数难以合理确定的困难并没有有效解决。
参数低秩设定不合理将导致数据补全模型过拟合或者欠拟合问题的发生。而选取不恰当的最大迭代次数将直接影响模型的补全精度以及计算消耗。为解决这些问题,研究人员提出将低秩分解问题转化成一个秩最小化函数问题。由于秩最小化函数问题是非凸的,因此研究人员使用核范数作为秩最小化函数的凸包络进而求解数据补全问题[13]。为提升数据补全模型的性能,P 范数[14]和迹范数[15~16]也被提出用于秩最小化函数的近似代替。基于不同张量分解技术构建了多种基于分解的数据补全模型。在此基础上,多种基于不同张量分解的秩最小化函数数据补全模型也被构建提出[17~19]。在文献[20]中,科研工作者通过使用带有顶帽正则化的低秩张量补全技术来完成红外小目标的检测任务。然而,大量的研究已经表明,秩最小化函数数据补全模型性能受到其模型内调节参数的直接影响。秩最小化函数数据补全模型规避了不合理的参数低秩以及参数最大迭代次数所带来的不利影响,但是与此同时却带来了新的参数确定困难。而且,由于范数是作为秩最小化函数的一种近似代替。所以,秩最小化函数数据补全模型存在着固有的系统误差。
为克服补全模型参数难以合理确定的困难,确保数据补全模型的性能,本文提出了一种基于进化算法NSGA2 的参数自确定数据补全模型。该模型在基于分解的数据补全模型基础上构建,因此不存在固有系统误差。在所提出的数据补全模型中,一个多目标函数优化模型被构建。通过进化算法NSGA2 执行进化选择操作合理的数据补全模型输入参数值被确定。对比试验结果表明,该模型所确定的模型输入参数值不仅避免了过拟合与欠拟合问题的发生,同时避免了计算资源的浪费,保证了数据补全的精度。
2 模型基础理论与算法
2.1 低秩矩阵分解补全模型
本文中所提出的数据补全模型是在低秩矩阵分解补全模型基础上构建的。以下是对低秩矩阵分解的一个简要概述。对于一个m×n维的矩阵,低秩矩阵分解可表示成如式(1)所示形式。
其中X表示一个已知的m×n维的数据矩阵,U和V表示通过对数据矩阵X进行低秩矩阵分解后得到的两个因子矩阵,r表示矩阵分解模型中的参数低秩。在基于分解的数据补全模型研究中,数据矩阵X的真实低秩r通常都是未知的。而且,伴随破损数据缺失元素比例的变化,数据矩阵X的真实低秩r也会随之发生改变,这也为确定补全模型合理的低秩值增加了困难。通常情况下,r需要满足如式(2)所示客观条件。
在基于低秩矩阵分解的数据补全模型构建中,引入了一个权重矩阵M,该矩阵用于表示缺失元素在破损数据矩阵X中的具体位置,如式(3)所示。低秩矩阵分解补全模型中,权重矩阵M是一个二元型矩阵。如果权重矩阵M中的一个元素为0,它表示数据矩阵X对应位置的元素丢失。如果权重矩阵M中的一个元素为1,它表示数据矩阵X对应位置的元素完整。
在运用低秩矩阵分解补全缺失元素信息的过程中,首先需要求得矩阵分解中U和V两个因子矩阵。然后将因子矩阵U与V进行相乘,其乘积结果即为破损数据矩阵补全完整后的结果。其中,因子矩阵U和V是通过迭代更新计算法则求得的。迭代更新计算公式如式(4)、式(5)所示。
2.2 进化算法NSGA2
NSGA2 是最经典的多目标进化算法之一,其在NSGA 的基础上提出。NSGA2 提出了快速非支配排序算法,在降低计算复杂度的同时保留了优秀个体。该算法引入精英策略有效提升了优化结果的精度。除此以外,拥挤度和拥挤度比较算子的使用克服了人为指定共享参数的缺陷,同时保证了种群的多样性。该算法优异的性能使其得到广泛应用。以下是对该算法运行步骤的简要概述。
步骤一:随机产生一个初始种群(第一代父代种群)。
步骤二:对初始种群进行非支配排序,并执行遗传算法基本操作产生第一代子代种群。
步骤三:首先,将父代种群与子代种群合并并对其进行非支配排序。然后对排序后的种群进行拥挤度计算。最后,根据种群中个体之间的非支配关系以及拥挤度产生新一代父代种群。
步骤四:对新一代父代种群执行遗传算法基本操作,产生新一代子代种群。
步骤五:重复步骤三和步骤四直至算法终止条件满足输出算法结果。
3 模型提出
3.1 基于NSGA2的参数自确定数据补全模型
日常工作生活中,我们所遇到的数据其真实低秩通常都是未知的。且研究表明数据的真实低秩将伴随数据缺失元素比例的变化而发生变化。这为确定一个合理的低秩参数值带来了巨大的困难。然而,基于分解的数据补全模型其性能受到了模型输入参数低秩与最大迭代次数的直接影响。因此,为了确定合理的模型输入参数值,确保补全模型的性能,本文提出了一种基于NSGA2 的参数自确定数据补全模型。
本文所提出的数据补全模型引入进化算法用于确定合理的模型输入参数,并针对数据补全问题的属性特征构造了多目标函数优化模型。在新的数据补全模型中,首先随机选取一部分模型输入参数的可能设定作为个体构建初始种群。然后,对初始种群执行进化操作,直至模型终止条件满足,确定补全模型输入参数最优解。如图1 所示是基于NSGA2的参数自确定数据补全模型流程图。
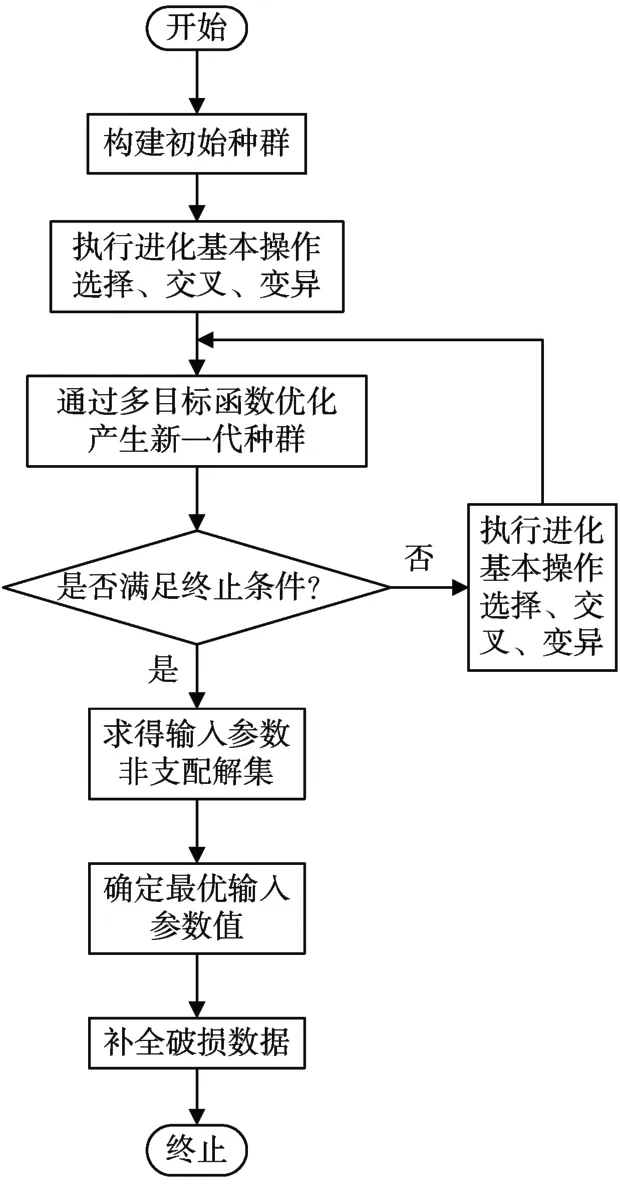
图1 基于NSGA2的参数自确定数据补全模型流程图
3.2 多目标函数优化模型
基于分解的数据补全模型原理起源于压缩感知原理。针对矩阵数据中的缺失元素补全问题也被称之为矩阵补全,这是一个不适定问题的反问题。因此它的解是不唯一的。为了能够精确补全破损的矩阵数据,要求矩阵数据必须具有低秩稀疏先验。除此以外,在补全问题的研究中要求补全后的矩阵与真实完整矩阵之间的误差尽可能地小。在现实补全问题中,人们还希望补全模型的时间损耗能够尽可能地小,尤其是当需要处理大量破损数据的时候。以上这些构成了基于矩阵分解数据补全模型的三个目标期望。基于此,本文提出了一个三目标的多目标函数优化模型,以下将对这三个目标函数分别进行阐述。
稀疏性目标函数:在矩阵分解中,矩阵X中的每一列都可以看作是因子矩阵U中所有行加权求和的一个结果。因子矩阵V中对应的每一列即为加权求和系数。因此,因子矩阵U被称为基矩阵,因子矩阵V被称为系数矩阵。矩阵分解中,矩阵的稀疏性越强意味着基矩阵U的规模越小。因此本文用低秩r与矩阵X列维度n之比表示矩阵稀疏性强弱。比值越小代表稀疏性越强。稀疏性目标函数公式如式(6)所示。
其中O1表示稀疏性目标函数。
补全误差目标函数:补全模型的根本目的是为了补全破损数据中丢失的元素信息。因此,确保数据补全的精度是至关重要的。在基于分解的数据补全模型中,研究人员通常使用F 范数来计算补全后的矩阵与真实完整矩阵之间的误差,如式(7)所示。
其中O2表示补全误差目标函数。
F 范数计算方法如下。首先,将矩阵中的所有元素进行平方求和。然后再对平方求和后的结果进行平方根运算,结果即为该矩阵的F范数。
时间损耗目标函数:在补全模型实际应用当中,对时间损耗尽可能小的要求是客观且必须的。本文通过计算CPU 起始时间差来表示模型补全过程中对时间的损耗。如式(8)所示。
其中O3表示时间损耗目标函数。
3.3 最优输入参数解选择策略
在基于NSGA2 的参数自确定数据补全模型中,进化算法通过进化操作确定了输入参数最优解集。然而,在实际应用中,基于分解的补全模型只需要一组输入参数值。因此,构建一套最优输入参数解选择策略是必要的。
在数据补全问题当中,由于低秩稀疏目标以及低时间损耗目标是与低补全误差目标相互矛盾的关系,因此人们总是希望能够以尽可能小的补全误差损失去换取更强的低秩稀疏性以及更小的时间损耗。基于此,本文通过设定补全误差损失最大阈值的方法从解集中选取输入参数最优解(该阈值设定为解集中最小补全误差目标值的0.1倍值)。
4 试验
为证明基于NSGA2 的参数自确定数据补全模型有效性,本文以破损图像修复问题为背景设计了多组对比试验。对比试验中所使用的破损图像其原始完整图像如图2 所示。对比试验过程中,人为清除图像矩阵内定量的元素信息,以形成满足指定缺失比率条件的破损图像。在不同元素缺失比率背景下,针对不同破损图像运用所提出的补全模型进行破损图像修复工作,并将补全结果进行对比分析,以证明所提出补全模型的有效性。对比试验执行的环境条件如下所述:PC(Intel(R)Core(TM)i7-4700MQ CPU@2.40GHz,8GB memory)。

图2 用于对比试验的原始完整图像
本文总共设计了四组对比试验用于证明基于NSGA2 的参数自确定数据补全模型有效性。第一组对比试验是以10%元素缺失比率下破损图像IMG1的修复问题为背景进行的。第二组对比试验是以25%元素缺失比率下破损图像IMG1的修复问题为背景进行的。第三组对比试验是以10%元素缺失比率下破损图像IMG2的修复问题为背景进行的。第四组对比试验是以25%元素缺失比率下破损图像IMG2的修复问题为背景进行的。
在对比试验当中,同一实验背景下本文通过将以最优解作为参数得到的补全误差与基于其它输入参数得到的补全误差进行对比,说明了由基于NSGA2 的参数自确定数据补全模型求得的输入参数其合理性,同时证明了新补全模型的有效性。对比试验结果如表1、表2、表3、表4所示。

表1 第一组对比试验结果表

表2 第二组对比试验结果表

表3 第三组对比试验结果表

表4 第四组对比试验结果表
观察表中的数据可以发现,无论是固定低秩值改变最大迭代次数值,还是固定最大迭代次数值改变低秩值,对比补全误差与相应参数增减变化量之间的关系表明,在参数变化量相等的情况下,基于输入参数最优解补全图像所导致的误差损失都是更小的。这充分说明了由新补全模型确定的输入参数以尽可能小的补全误差损失换取了更强的低秩稀疏性以及更小的时间损耗,具有合理性。
5 结语
在数据补全问题的研究中,基于分解的数据补全模型存在着模型输入参数难以合理确定的困难,而秩最小化函数补全模型存在着固有的系统性缺陷。为了确保数据补全模型的性能,一种新的基于进化算法NSGA2 的参数自确定数据补全模型在本文提出。新的补全模型通过进化算法执行进化操作自行确定模型输入参数值。由模型确定的输入参数值在追求补全精度的同时兼顾了良好的低秩稀疏性,最小化了模型计算时间损耗。在未来的工作中,我们将拓展该模型到更高阶破损数据修复问题当中。
