融合算法改善后在物流配送中的应用∗
2023-10-20钱怡杉
钱怡杉 何 乔
(上海理工大学光电信息与计算机工程学院 上海 200093)
1 引言
近年来许多学者对智能算法和启发式方法以及其在定位路由问题(LRP)上的应用进行了大量的相关问题研究。Barreto 等[1]提出了一种基于分层和非分层聚类技术的聚类分析过程,并采用多个邻近测度来获得启发式算法,然后采用序贯启发式算法和聚类技术来解决LRP 问题。Lei 等[2]研究了考虑两级路由的两级选址问题,模型建立时考虑了配送中心的数量及其位置。为了解决这一问题,提出了一种带路由启发式的混合遗传算法,实现了一种近似最优解。Derbel等[3]提出了一种将遗传算法(GA)与迭代局部搜索(ILS)相结合的求解定位路由问题(LRP)的混合方法。Ting 等[4]提出了一种多蚁群优化算法,在算法优化过程中,通过信息素更新来求解具有路径和仓库容量约束的LRP 问题。Escobar 等[5]提出了一种求解位置路由问题的两阶段混合启发式算法,并在算法中引入了随机扰动过程,避免了局部最优。Marinakis[6]提出了一种求解车辆路径问题的混合算法。该算法将粒子群优化算法与2-opt 和3-opt 局部搜索相结合。Nadizadeh[7]提出了一种包含随机模拟的混合算法和一种具有模糊需求的动态容性LRP 的局部搜索方法。Rodríguez-Martín[8]摘要提出了一种具有决策树和切割平面方法的支路定界算法作为枢纽选址和路由问题的边界计算方法。Ting[9]针对离散动态泊位分配问题,提出了一种基于局部搜索的粒子群算法(PSO)。Norouzi[10]针对周期车辆路径问题,提出了一种改进的粒子群优化算法,该算法包括选择/启发式算法和内环交换策略。Sašo Karakatič[11]介绍了一种求解多站车辆路径问题的遗传算法。他们指出,将遗传算法与其他智能算法合理结合,可以避免具体方法的不足。
在物流配送每个分区区域,进一步研究vrp 变体,以解决更复杂的vrp变体,例如带时间窗口的车辆路径问题(Vrptw)[12]。同时送货和提货的车辆路径问题。配送区域划分问题极大地减轻了大规模物流配送网络优化的计算负担,从而促进了大城市物流城市规划过程。Rodrigue[13]研究了货运配送的区域性,并对北美和欧洲的门户物流实践进行了比较分析。Basligil 等[14]研究了第三方物流服务提供商的两阶段配送网络优化问题,其中第一阶段是分配问题,第二阶段是进一步优化配送网络。Hemmelmayr[15]针对两级车辆路径问题和LRP,提出了一种自适应的大邻域搜索算法,其中LRP 是2E-VRP 的特例,车辆路径在第二级执行。Govindanet[16]研究了具有时间窗的两级定位路由问题,在第一阶段确定了数量和位置设施,并在第二阶段优化了交付给客户和路线的产品数量。然而,据我们所知,很少有研究用使用分布区域划分技术来简化二级物流网络优化。
与以往的研究相比,本文的主要工作体现在:1)构建配送区域划分模型,最大限度地降低二级物流配送网络的总成本。2)设计了一种基于粒子群算法(PSO)和模拟退火算法(SA)相结合的混合算法求解模型。这种新技术可以在客户聚类问题和VRP 之间建立紧密的联系,为大大降低后续VRP的复杂度奠定了基础。
2 理论基础
粒子群算法(PSO)是一种基于元启发式的搜索算法。在解决各类较为复杂的问题时,粒子群算法需要做的是平衡处理全局搜索和局部搜索,在处理最优问题时,我们需要使用粒子群算法的全局搜索能力,让搜索范围收敛于某一区域,然后再采用精准的搜索方式找到极值。我们对惯性权重线性递减粒子群算法(LDWPSO)做了介绍,随着迭代次数增加,惯性权重渐渐减小,粒子从全局最优渐渐转变为局部最优。但是,线性惯性权重算法仍存在一些缺陷。当实际问题比较复杂,惯性权重已经随着迭代次数的增加而逐渐减少,但此时粒子没有找到全局最优,陷入了局部最优。这样一来,会得到较大的误差值。为了解决这个问题,进一步提高粒子群优化算法的性能,我们提出了一种惯性权重非线性递减的粒子群优化算法(NLDWPSO),该算法中惯性权重表示如下:
u为定义为衰减因子,经过测试取值在1.8 左右为宜,在该算法中,t的初始值是0,此时粒子的搜索能力最强,随着t 的增加,惯性权重非线性地减小。

图1 NLDWPSO算法流程图
3 实验仿真及分析
本节使用Griewank 函数对NLDWPSO、LDWPSO、PSO三种算法进行对比分析,参数设置如下。
NLDWPSO 的种群数量popsize=50,最大活动半径为[-80,80],维度dim=25,初始惯性权重ws=0.87,最终惯性权重we=0.31,最大限制速度为vmax=7,c1=c2=1.49445。
LDWPSO 的种群数量popsize=50,最大活动半径为[-80,80],维度dim=25,初始惯性权重ws=0.87,最终惯性权重we=0.31,最大限制速度为vmax=7,c1=c2=1.49445。
PSO 的种群数量popsize=50,最大活动半径为[-80,80],维度dim=25,初始惯性权重ws=0.87,最终惯性权重we=0.31,最大限制速度为vmax=7,c1=c2=1.49445。
仿真迭代次数为900 次结束,对三种算法进行150 次,取平均值,定义适应度值大于0.1 视为非收敛,该算法的仿真结果如表1。

表1 Griewank函数性能比较
从表1 可以得出,在Griewank 函数的测试中,NLDWPSO 和LDWPSO 平均适应度值均优于PSO算法,NLDWPSO 所需收敛次数最多,收敛速度最快。在算法精度上,前两种算法的寻优效果无明显区别,均优于PSO;在收敛次数上,NLDWPSO 是80次,LDWPSO 是76 次,两者相差不多,PSO 表现最差,是40 次。但前两种算法依然存在陷入局部最优的问题,不能保证粒子达到全局最优解,这说明改进的算法在多峰值的算法中,依然容易陷入局部最优解,后续拟引入模拟退火算法继续进行优化。
接下来我们引入了模拟退火算法,模拟退火算法具有全局寻优的优点,可以接受较差的点,扩大寻优范围,能够很好地跳出局部最优解,这种可以抑制粒子早熟的现象正好是粒子群所需要的,所以融合两种算法各自的优点,弥补各自的缺点,能够很好地提高算法的性能。本次实验我们求解最小值。在融合的算法中把粒子群算法作为主要的算法,首先对粒子群算法优化作为一个小的优化过程,同时模拟退火算法在一定范围内进行优化。
改进算法的流程如下:
步骤1:设置种群规模N,粒子群的最大迭代次数MaxIter,对每个粒子的速度vid和位置xid进行初始化,然后计算每个粒子的适应度值f(xid),然后将各自粒子的适应度值存储到个体极值pbestfit 中并保存相应的个体极值点pid,比较每个粒子的适应度值,找出最优的适应度值存到种群最优值gbestfit中并保存相应的种群极值点pgd。
步骤2:设置初始温度Temp0。
步骤3:根据式(2)和式(3)更新粒子群速度和位置得到新的粒子速度、位置分别为vid(t+1)、xid(t+1)。
其中t 代表迭代次数,w(t)为第t 代的惯性权重,初始值惯性权重为wmax,惯性权重w(t+1)从wmax随迭代次数逐渐非线性下降到wmin,u为某一常数。
步骤4:计算粒子i 第t+1 代和第t 的适应度值的差值∆f=f(xid(t+1))-f(xid(t)),if ∆f<0,则接受新的位置和速度,else ∆f>0,先计算接受概率
步骤5:进行退温操作,本文采用比较常用的线性退温操作Temp(t+1)=λTemp(t),其中初始温度为Temp0=f(pgd)/In5。
步骤6:如果达到终止条件(迭代次数达到MaxIter 或者最优解不再变化,即找到最优解)来终止算法,种群的最优位置即为最优位置,种群的最优适应度值即为最优值。否则跳转到步骤4,继续往下执行。
NLDWPSO-SA 的种群数量popsize=50,最大活动半径为[-80,80],维度dim=25,初始惯性权重ws=0.87,最终惯性权重we=0.31,最大限制速度为vmax=7,c1=c2=3。降温系数λ=0.84。
NLDWPSO 的种群数量popsize=50,最大活动半径为[-80,80],维度dim=25,初始惯性权重ws=0.87,最终惯性权重we=0.31,最大限制速度为vmax=7,c1=c2=3。
LDWPSO 的种群数量popsize=50,最大活动半径为[-80,80],维度dim=25,初始惯性权重ws=0.87,最终惯性权重we=0.31,最大限制速度为vmax=7,c1=c2=3。
PSO 的种群数量popsize=50,最大活动半径为[-80,80],维度dim=25,初始惯性权重ws=0.87,最终惯性权重we=0.31,最大限制速度为vmax=7,c1=c2=3。
仿真迭代次数为900 次结束,对三种算法进行150次,除去非收敛次数(大于0.1),取平均值,该算法的仿真结果如表2。
从表2 和图2 可以看出,在Griewank 函数中NLDWPSO-SA 平均适应度值和最好适应度值都要比LDWPSO 和LDWPSO 好,NLDWPSO-SA 精度比NLDWPSO 更好,其次是NLDWPSO 和LDWPSO,最差的是PSO,由此可见改进的NLDWPSO 在Griewank函数中性更好。
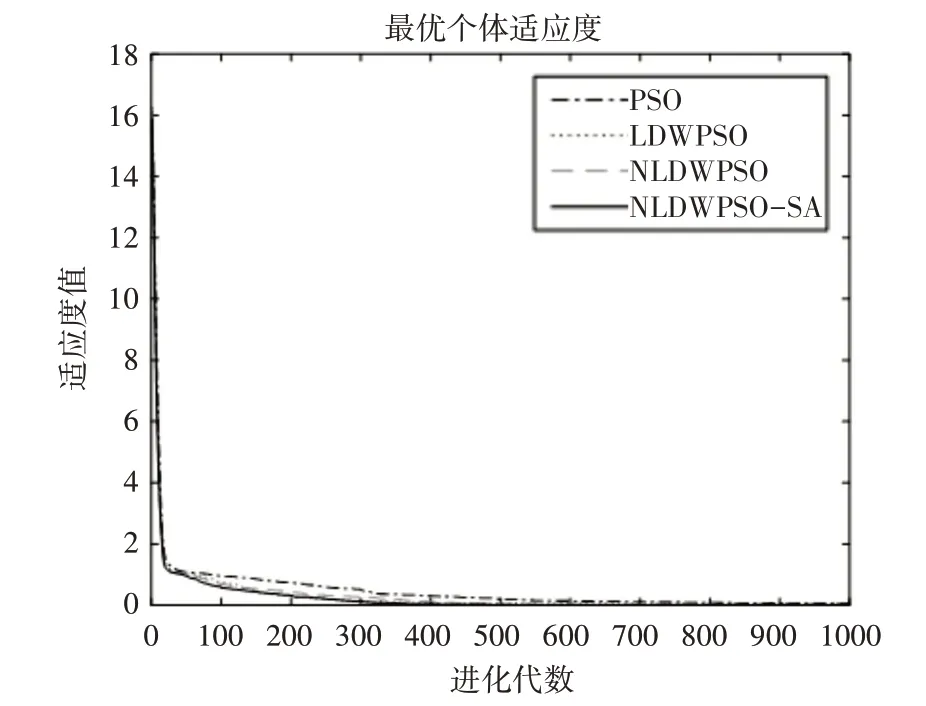
图2 Griewank函数适应度值
4 实际应用
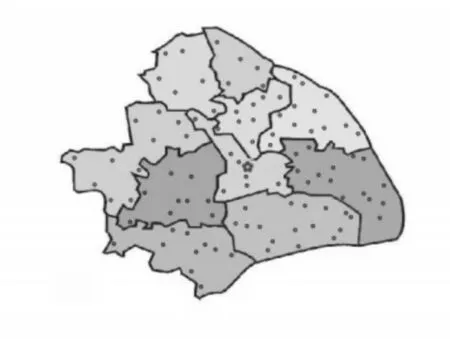
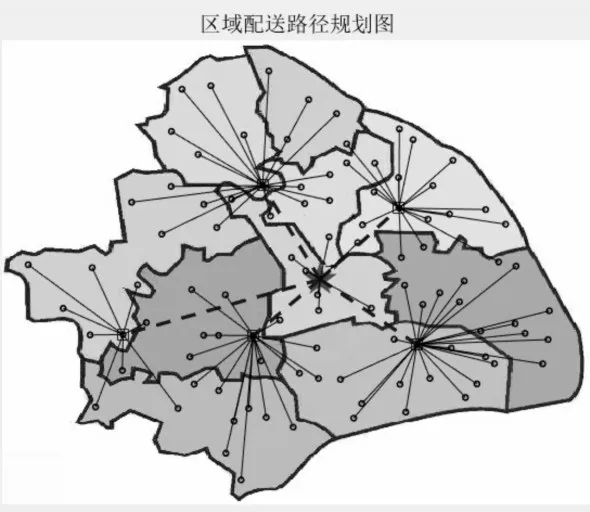
子编码方案与评价函数设计结合在算法计算过程中是非常重要的,对于二级物流配送网络中的物流配送区域划分问题,应考虑各物流设施的配送能力。因此,本文提出了一种二维粒子编码方法。粒子的第一维表示为自然数序列:1,2,3,…,j,…,L,其中L(L 图3 上海地图 图4 分配单元的空间分布 图5 区域配送路径规划图 本文采用100 个配送单元,一个物流中心,若干个配送中心,每个配送中心对应一个需求点,配送中心将从100 个配送单元中选出,这样可以节省配送中的配送费用,模型参数:G 是15000,λ=4000,ρc=10,ρb=20,vb=15,vc=45。算法参数设置:粒子群数popsize=100,学习因子c1=c2=3,最大迭代次数maxgen=300,降温系数λ=0.84,100 个配送单元需求分别为16,15,20,3,7,10,7,18,17,15,9,15,9,16,17,15,6,1,20,13,16,15,2,15,1,1,8,14,17,18,3,17,18,16,15,1,20,3,15,10,6,8,6,14,1,2,10,16,15,17,2,7,19,14,10,16,10,14,2,10,14,10,5,22,10,7,3,18,17,20,2,15,5,9,18,10,18,8,19,10,6,3,10,15,9,1,3,22,9,17,10,17,10,2,19,15,1,10,16,12,单位为吨。 当选择物流中心个数为5 时,物流中心设置一个。NLDWPSO-SA 总费用为59650.1254 元,其中,一级配送费用9958.9243 元,二级配送费用14691.201 元,物流中心建设成本15000 元,配送中心建设成本20000元。 物流中心坐标:(263.446,228.2575)。 5 个 配 送 中 心 坐 标 为(328.7187,160.378)(100.4908, 280.8296) (208.2517, 281.7222)(215.9508,138.8783)(343.5597,290.2712)。 本文对粒子群算法进行改进,引入了非线性递减的惯性权重,比之线性权重,不易陷入局部最优,搜索精度更高。通过Griewank 函数测试后比较发现,收敛速度虽优于粒子群算法,但是在多峰值的算法中,依然容易陷入局部最优解,因此使用模拟退火算法来跳出局部最优解,该算法在Griewank函数测试中的效果明显比粒子群算法更好。在此基础上,本文使其应用在二级区域配送网络中,以上海市地图为例来寻求最优解。实验结果表明,该算法可以得到最优解决方案,且明显优于其他三种算法。此外,所提出的方法在其他研究领域有很大的应用潜力。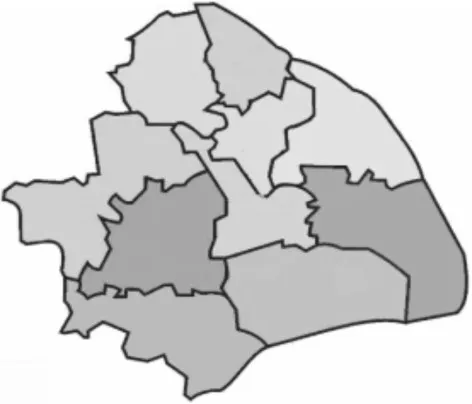
5 结论
