多轨道时序InSAR拟稳基准平差方法研究

杜钊锋 周晓敏 程小凯 郑文科 朱新杰

1 自然资源部第一大地测量队,西安市测绘路4号,710054

在利用时序InSAR(interferometric synthetic aperture radar)技术进行大范围地面沉降监测时,通常涉及多个轨道的数据融合,其中最主要的问题是不同轨道形变场参考基准的统一[1]。许多学者[2-3]针对多轨道时序InSAR技术展开研究,Shirzaei[4]和Pepe等[5]对多轨道多时相InSAR拼接算法进行分析,提出对公共区域目标点在空间范围和时间序列的拟合进行多轨道数据基准统一的方法。部分学者[1,6]利用Envisat、Radarsat、Sentinel等卫星数据对我国主要沉降区开展大范围InSAR监测,通过计算多轨沉降结果的重叠区偏移值,将同名点的形变速率取算术平均,以实现大区域形变速率的镶嵌。文献[7-8]对大范围多轨道基准转换与数据拼接问题作进一步研究,分析引起相邻轨道沉降速率差异的因素,提出采用区块法、插值法等方法解决异轨永久散射体(persistent scatterer, PS)沉降量偏差。

然而,上述研究大都基于重叠区评估恒定的偏差量,通过消除偏差量来实现基准统一,但该类方法容易将不同轨道参考基准的差异当作误差组分,尤其对形变量较大的区域其拼接后的形变速率容易产生扭曲。因此,本文通过对多轨道时序InSAR误差源进行分析与处理,引入拟稳基准平差方法,消除多轨道形变监测结果的偏差,达到不同轨道形变场参考基准的统一,增强多轨道时序InSAR技术监测大范围地面沉降的适用性。

1 多轨道时序InSAR误差源分析

1.1 入射角引起的差异

入射角引起的差异主要由SAR斜视特征所决定,InSAR数据处理得到的直接结果为视线向变化量。如图1所示,S1和S2表示相邻轨道2次卫星过境,假设某点真实地面沉降量为L,SAR数据近地点和远地点入射角分别为α、α+β,雷达视线向变化量分别为Lcosα、Lcos(α+β),差值为ΔL=Lcosα-Lcos(α+β)。以哨兵数据为例,当真实地面沉降速率为50 mm/a时,雷达视线向近地点和远地点最大沉降偏差为12.3 mm/a;当真实地面沉降速率为100 mm/a时,雷达视线向近地点和远地点最大沉降偏差为24.5 mm/a。由此可以推断,地面沉降越严重的区域由入射角引起的差异越明显。

图1 雷达入射角差异示意图Fig.1 Diagram of radar incident angle difference

本文研究主要考虑的是垂直方向地面沉降量,水平方向变化量由地壳水平运动速度场决定,属于板块运动尺度,在本文研究区内可认为是均质的。因此,数据处理中将视线向形变量转换到垂直方向,不考虑水平方向位移。

1.2 参考点引起的差异

参考点引起的差异与相干目标点距参考点的距离有关,一般来说,参考点本身也存在一定程度的年际和季节性变化,选取参考点首先应考虑稳定性,即参考点在监测周期内处于相对稳定的状态,但随着监测范围的逐步扩大,参考点距离增加,由单个参考点得到的形变量逐渐失真。朱武等[9]对多参考点PS-InSAR数据处理方法进行研究,对比单参考点和多参考点下的形变场,认为多参考点结果比单参考点结果更接近地面观测资料。前人研究范围较小,而当研究范围不断扩大时,参考点引起的差异将更加明显。

本文数据处理选择多参考点,将综合分析选取的拟稳点作为多参考点进行数据处理。为保证各条带形变参考基准的统一,相邻条带间至少保证重叠2个拟稳点。

1.3 轨道残余误差

轨道残余误差主要由轨道估计的偏差所致,在数据处理结果上体现为趋势性偏差,评估轨道残余误差的数学模型可表示为:

1阶:z=ax+by+c

1.5阶:z=ax+by+cxy+d

2阶:z=ax2+by2+cxy+d

3阶:z=ax3+by3+cx2y+dy2x+ex2+

fy2+gxy+h

本文采用精密轨道星历文件计算基线,考虑到按上述模型进行轨道误差评估时可能导致形变分量被误评估为轨道误差,因此数据处理中暂不进行轨道残余误差的评估。

1.4 大尺度地形相关性误差

InSAR干涉测量中通常将大气延迟分解为大气垂直分层延迟和水平紊乱延迟[10],其中,大气垂直分层延迟主要由静力学延迟和小部分天顶湿延迟组成,该部分误差与地形具有较强的相关性;水平紊乱延迟则主要由天顶湿延迟组成,该部分误差在时间上具有随机性特征。

本文主要研究大区域垂直形变场基准的统一,大气延迟以低频信号为主,与地形具有较强的相关性,因此采用GACOS模型[11]对大气延迟进行改正,再计算平均沉降速率和形变时间序列。评估完上述误差组分后,其余误差主要由大气误差组成,以高频信号为主,通过滤波方法即可去除,滤波时需考虑空间窗口和时间维度,保留一定程度的季节性变形幅度,最后得到相干目标点的平均沉降速率和形变时间序列结果。

2 拟稳基准平差方法

拟稳平差方法是针对变形监测网中存在部分稳定点和部分不稳定点的情况,不同于监测网的秩亏自由网平差计算,拟稳平差中将所有点都当作未知数进行解算,顾及到变形监测网中存在部分相对稳定的点(称为“拟稳点”),对该类点附加相关的未知量范数极小的条件,此前的秩亏自由网便能求得唯一解。由拟稳点构成的参考基准则称为监测网的拟稳基准。拟稳平差主要应用于沉降监测分析,如水准网沉降分析,本文将其应用于InSAR监测的地面沉降平差计算与分析。

设不稳定点的未知数为X1,稳定点的未知数为X2,则误差方程为[12]:

(1)

式中,n表示InSAR监测结果中PS点由不同参考点所组成的多余观测量,t1和t2分别表示不稳定PS点和稳定PS点数量,t1+t2=t,R(A)=r,秩亏d=t-r,A2维数大于秩亏数,即m>d,在InSAR监测的地面沉降网中m>1,必须有2个或2个以上的拟稳点。R(A1)=t-m,A1为列满秩矩阵。观测值l的权重P按距离定权,类似于水准监测网,P满秩,按照最小二乘原则VTPV=min,构成法方程组为NX=ATPl,可写成:

(2)

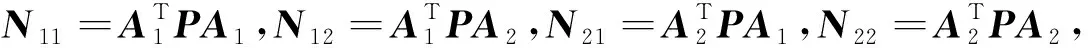
(3)

(4)

将式(3)、(4)代入式(1)得到改正数的计算公式:

(5)

由以上公式可以看出,拟稳平差是在最小二乘原则和最小范数条件下得到的,与自由网不同之处在于最小范数条件是仅相对拟稳点而言,在使监测网形不扭曲的同时,得到监测网拟稳基准的变化量。

3 实验数据与结果分析

3.1 数据源

根据研究区范围获取SAR影像,本文选择Sentinel-1卫星干涉宽幅成像模式升轨数据,影像空间分辨率为5 m×20 m,覆盖研究区共10景,每景超100期数据,共计1 120期数据,每期数据覆盖范围约为250 km×150 km,SAR数据如表1所示。

表1 SAR数据Tab.1 SAR data

3.2 处理结果

本文采用StaMPS方法[13]进行时序InSAR数据处理,基于幅度离散和相位空间相关特性选点,该方法能够在城区和郊区识别出较多的PS点。数据处理中依据空间基线、时间基线、相干性等因素选取主图像,40条带、142条带、69条带主图像分别为2018-11-28、2018-03-04、2018-12-24,干涉对空间基线在[-150, 150]之间,依次进行图像配准、干涉处理、去除平地效应、计算候选点、去除噪声点、相位解缠、评估大气影响相位、轨道误差相位、地形残差相位等[14],将形变相位转换为年均沉降速率和时间序列变化量,即为初始数据处理结果。

本文研究区主要以平原为主,北部和西部有一定范围的山区,一般认为山区较少发生大范围的地表形变,选定为InSAR参考点。各条带初始数据处理结果均是以InSAR参考点为基准,类似于水准监测网中给定固定点的间接平差计算结果。

在拟稳点选取时,充分考虑InSAR初始数据处理结果中变形量较小区域的空间分布,同时综合已收集资料中CORS站地表形变结果、国家高程基准网基岩点分布、大地控制点垂向变化结果等因素,首先选取一定数量的拟稳点作为备选点,通过一致性检验剔除相对不稳定的点,最终确定参与平差的拟稳点。如图2所示,40条带、142条带、69条带拟稳点数量分别为5、5、4。通过编写MATLAB代码实现多轨道时序InSAR拟稳基准平差数据处理,该方法可以有效降低单参考点或区域造成的系统偏差,尤其是可以抑制由于参考距离较远造成误差传播递增的现象,使测量平差计算结果更加符合客观规律,提升地面沉降监测网的可靠性。

经过拟稳基准平差处理,得到华北平原40、142、69条带InSAR数据处理结果,将年均沉降速率和年际沉降速率进行叠加,结果如图3所示。从图中可以看出,各条带之间沉降速率过渡自然,无明显分界,说明InSAR数据处理整体情况良好。

通过年际沉降速率(图4)可以发现,沉降漏斗演变和发展各有规律,华北平原主要沉降漏斗在2019年最为严重,漏斗逐年变化形态也有所差异,北京-天津地区沉降漏斗呈逐年减少趋势,河北地区(巨鹿县-南宫市、临漳县-广平县-曲周县、景县-阜城县、饶阳县-肃宁县-高阳县)主要沉降漏斗呈持续高速发展趋势,沉降速率为-150～100 mm/a。沉降漏斗变化发展与年度降水量、地下水开采量、南水北调补水等存在一定关系,待后续进一步研究。

图4 年际沉降速率Fig.4 Interannual subsidence rate

依据InSAR监测结果,采用克里格方法对InSAR相干目标点平均沉降速率进行插值计算,表2为平均沉降速率分类统计结果。

表2 InSAR结果平均沉降速率分类统计Tab.2 Statistics of average subsidence rate of InSAR results

3.3 精度评定

精度评定以内符合精度为主,对40-142重叠区域、142-69重叠区域内PS点进行分析,分别提取PS点各年度平均沉降速率,通过建立一一对应关系,将各年度平均沉降速率进行差值,计算其平均误差和中误差,40-142重叠区域建立PS点样本数目542 184个,142-69重叠区域建立PS点样本数目1 389 857个。

分别对初始数据处理结果和拟稳基准平差结果按照上述方法统计重叠区域PS点速率差值的平均误差和中误差,结果如表3(单位mm/a)、表4(单位mm/a)所示。从表中可以看出,通过拟稳基准平差后内符合精度统计结果明显优于初始数据处理结果。由图5(a)可知,拟稳基准平差后平均误差优于5 mm,中误差优于9 mm。

表3 初始数据处理结果内符合精度统计Tab.3 Statistics of internal coincidence accuracy of initial data processing results

表4 拟稳基准平差后内符合精度统计Tab.4 Statistics of internal coincidence accuracy after quasi-stable datum adjustment

图5 InSAR结果与CORS站结果对比Fig.5 Comparison of InSAR and CORS results

本文通过研究区内10个CORS站1999～2019年位移计算结果(中国地震局地壳形变台网中心提供),与拟稳基准平差后的时序InSAR进行对比分析。将CORS站与InSAR结果归算到地表垂向变化时间序列上进行数据对比,结果如图5(b)～(h)所示。由图可知,两者吻合程度较好,BJFS、HELY等站点变化幅度与InSAR结果较为一致;BJSH、BJYQ、SXYC等站点变化幅度相比InSAR结果略小;HECX、TJBH、TJWQ等站点连续多年的地面沉降趋势与InSAR结果整体一致,两者存在一定程度的差异主要是由于空间位置无法完全重合所致,CORS站点为特定点位,而InSAR结果的相干目标点代表一定区域的面散射体特征[15]。总体来讲,CORS站位移计算结果与InSAR结果在刻画季节性变化的细节形变信息上较为一致,从外符合精度角度进一步说明InSAR结果具有可靠性。

CORS站优势主要体现在单站点数据采样足够丰富,计算结果更利于表达年际变化规律和季节性变化规律,但站点分布数量少。InSAR监测优势主要体现在面状地面沉降信息的提取,大数据量更有利于刻画空间分布的细节信息,但在单点时间序列拟合上数量相对较少。

4 结 语

本文以我国重点沉降区(华北平原)为研究区,分析多轨道时序InSAR误差源,综合考虑水准基岩点、InSAR形变参考点、CORS站等因素选取拟稳点,提出采用拟稳基准平差方法进行多轨道时序InSAR平差计算,实现大范围多轨道InSAR垂直形变场基准的统一。研究结果表明,经过拟稳基准平差计算后,研究区各条带之间沉降速率过渡自然,无明显分界,拟稳基准平差后内符合精度统计结果明显优于初始数据处理结果,拟稳基准平差后平均误差优于5 mm,中误差优于9 mm,说明时序InSAR拟稳基准平差结果内符合精度良好。对比分析研究区CORS站垂直方向变化量与InSAR结果发现,两者吻合程度较好,从外符合精度角度说明时序InSAR拟稳基准平差结果具有可靠性。

致谢：感谢中国地震局地壳形变台网中心提供GNSS基准站位移结果。