包含系统因素的磁通门经纬仪比测模型的建立

古云飞 黄 好 李文一

1）中国陕西 710068 陕西省地震局西安地震监测中心站

2）中国天津 300161中国地震局第一监测中心

0 引言

磁通门经纬仪（也称DI仪）是一种用于测量地磁偏角D和地磁倾角I绝对值的仪器，它由无磁经纬仪、磁通门传感器、磁通门检测器3部分组成，可用于固定地磁台站测量和野外流动测量，是目前使用最广泛的地磁绝对测量仪器之一（Jankowski et al，1996；宋思璇等，2020）。

根据目前的研究结果，磁通门经纬仪测量误差来源主要有：修正系数（格值）、温度、零点偏移、分辨力，还有与之同步观测的磁通门磁力仪的X、Y、Z三轴正交度、灵敏度（姚远等，2016；王晓美等，2017；张涛等，2018；刘浩等，2022）、偏置量、D分量定向、观测墩漂移、台站供电系统稳定性等（屈文斌，2020；车濛琪等，2020；罗玉芬等，2021；陈贤等，2021；迟铖等，2021）。Marsal等（2007）提出,日常观测实践中系统效应会引起误差，并分析了磁通门经纬仪由机械结构引入的不确定度，该问题可通过目前已广泛使用的“四位置”测量方式解决。Jankowski等（1996）对单台仪器测量时的影响量进行了分析，但仅在定性层面进行了概述。张策等（2020）对自动磁偏角磁倾角测量仪的误差进行了分析研究，与本文所讨论的人工仪器有一定差别。

所有台站的磁通门经纬仪需要定时进行比对测量（简称比测），其中最重要的指标是“仪器差”，即被测试仪器与标准仪器测量磁偏角和磁倾角结果的差值，属于一种测量误差，但是，针对该指标的定量误差分析研究或者不确定度评定方法，目前尚属空白，所以比测的结果也无相应的误差或者不确定度表示。这导致我国地磁台网对仪器指标进行合格性判定时经常出现错误，尤其当结果在最大允许误差限附近时更容易误判。针对类似问题，解决办法就是对测量结果引入不确定度。传统的磁通门经纬仪比测模型只体现了理想状况，没有综合考虑测量过程中的多种系统因素，并不适用于开展不确定度评定。

综上，本文将建立包含系统因素的磁通门经纬仪比测模型，并通过对测量结果进行不确定度评定、合格判定及数据比较来验证该模型的正确性与实用性。

2 基本原理

“近零法”和“指零法”是地磁测量主要采用的2种方法，二者在基本原理上没有区别，均采用了经纬仪的“四位置测量”方法，仅在操作和计算方法上略有不同。文中以近零法的测量为例进行分析。

仪器差测量基本流程如图1所示。首先得出被测仪器及标准仪器的D的基线值DBX、DBS，二者之差为EDX，其中角标X表示被测仪器，S表示标准仪器、B表示基线值，D、I表示磁偏角和磁倾角，即被测仪器与标准仪器测量磁偏角D的差值，也称D的仪器差。即

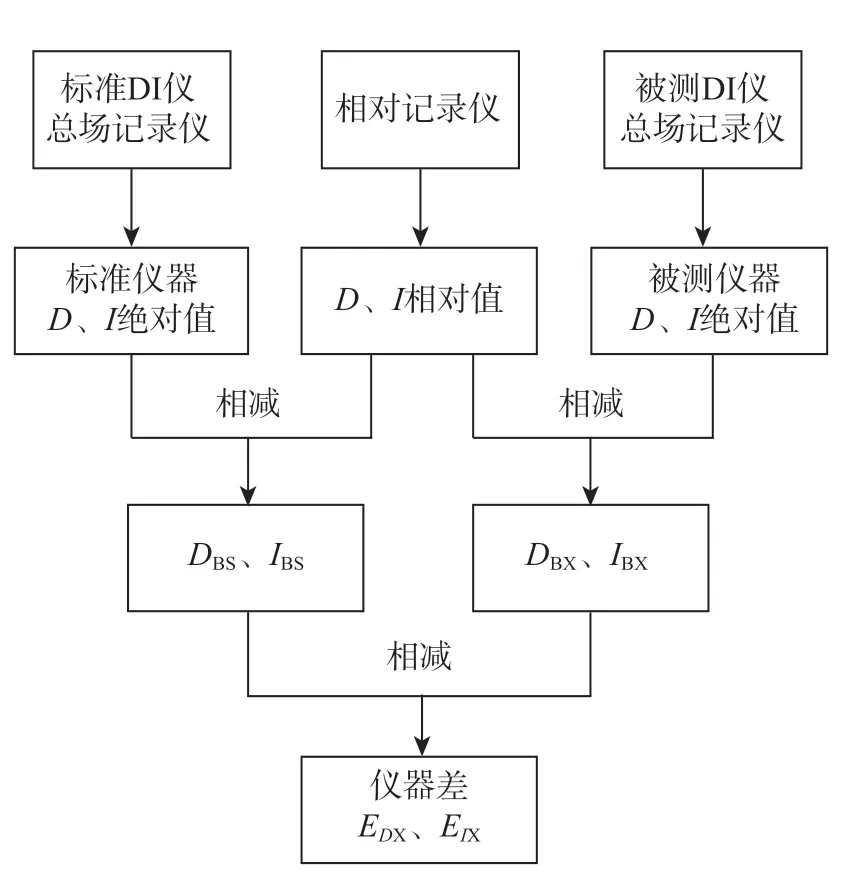
图1 仪器差测量基本流程Fig.1 Basic process of the instrument difference measurement

EIX即为磁倾角I的仪器差。

需要说明的是，仪器差本质是测量误差，根据计量规范《JJF1001—2011 通用计量术语及定义》对“测量误差”的定义，EDX、EIX的正负号应与传统定义相反，本文采用该规范写法。

3 系统因素分析

根据前文分析，现有的比测方法并未考虑测量过程中各干扰因素的影响，因此测量结果会有较大不确定度。以下对其中已知的、可分析的不确定度来源，即系统因素进行分析。由未知因素引起的、或不受控的随机因素引起的不确定度，一般可通过重复测量或者剔除异常值的方法消除，不做分析。

2.1 相对记录仪日变影响

在理想状态下，基线值为常数，但由于磁通门磁力仪的三轴不能达到完全相互垂直，且在仪器架设时存在定向误差，导致记录的地磁三分量（D、H、Z）变化曲线会产生畸变，因而基线值也发生变化，这种变化称为日变，其在D和I上的变化量即为δRD、δRI，单位为“′”。图2展示了乾陵地磁台GM4-XL型磁力仪与FGM01型磁力仪日间10 h的基线值，也就是日变记录。

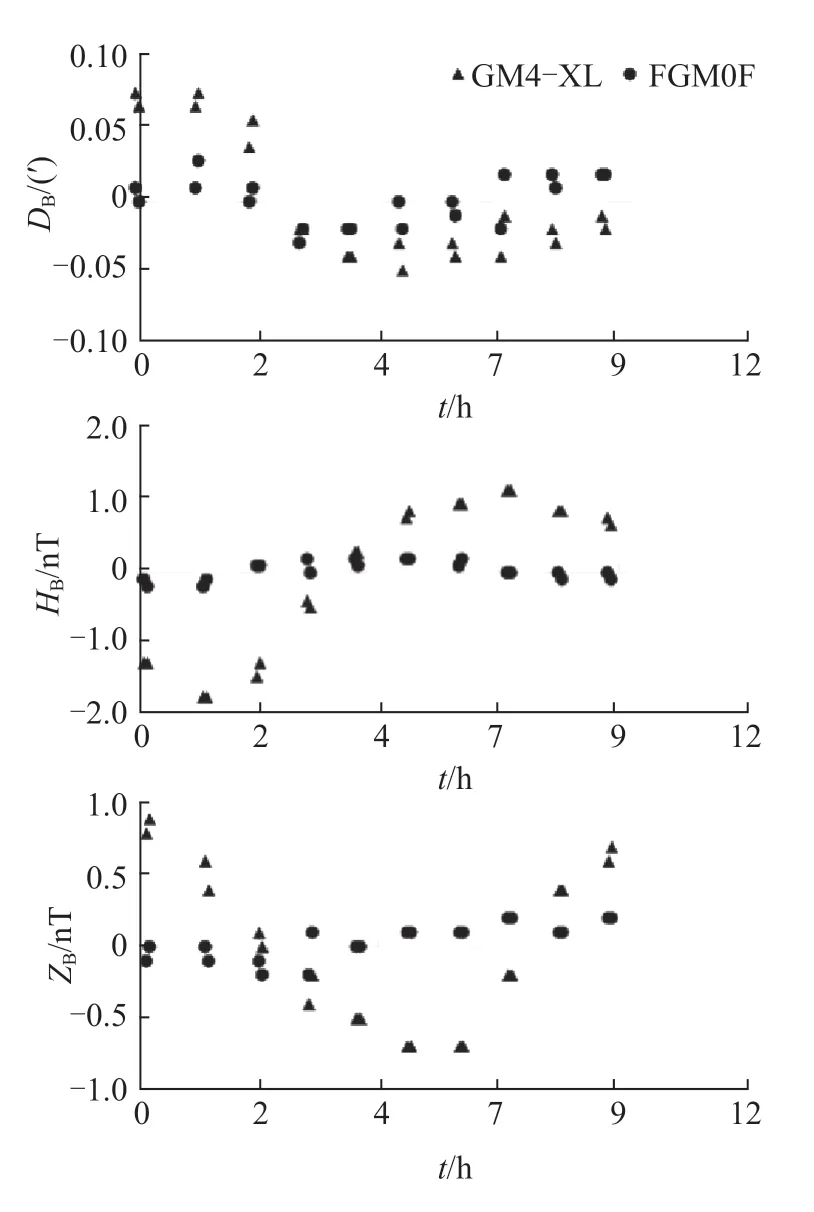
图2 2台仪器日变曲线对比Fig.2 Comparison of daily variation curves of 2 fluxgate theodolites

2台仪器都呈现出变化的曲线，因此无论选择哪一台仪器，只要选用不同时间点的基线值进行仪器差计算，就可能引入日变带来的误差，所以，在去除仪器日变引起的误差后，式（1）、式（2）变为

2.2 温度的影响

以近零法测量磁偏角D为例，测得的偏角D修正值

式中，ΣΔSX/4是4个位置检测计示数在赋予正负号后的值的平均，CX是被测仪器的修正系数，T=3438′/rad，是弧度转换为角度分的参数，H是测量点位磁场水平分量概值，为常量，单位nT。实际上，由于4个位置测量时有一定时间差，由测量时环境温度变化导致的基线值失稳情况时有发生。

图3为榆林地磁台观测室2020年的温度变化与仪器零点偏移变化的关系，二者具有明显的相关性。因此在测量时，若温度变化过大，则一定会对零点偏移量产生影响，继而影响到测量结果。根据实际，设测量前后温度为线性单调变化，4个位置温度变化引起的偏移量被算入了修正值，该偏移量可按如下方法计算

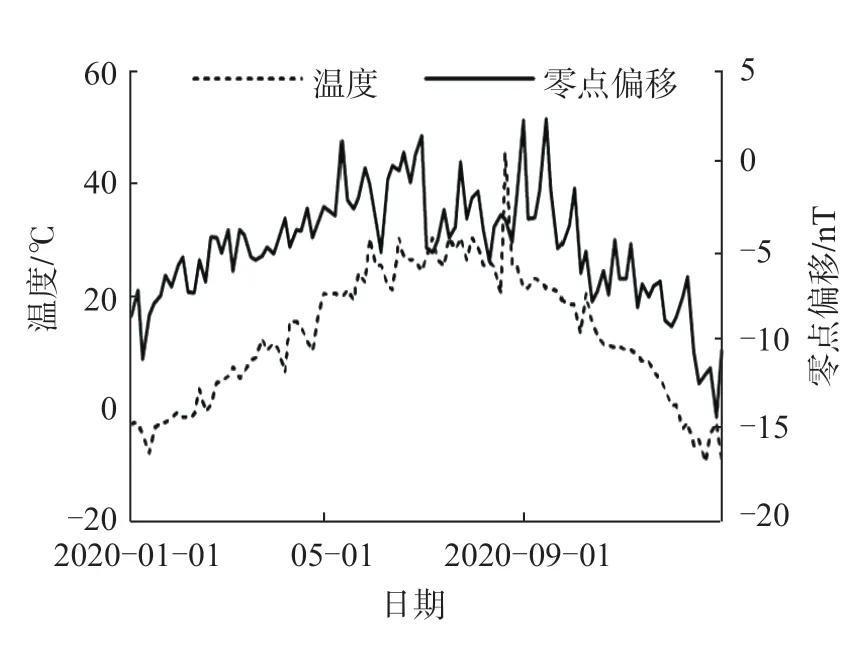
图3 温度与零点偏移的变化Fig.3 Zero shift changes with temperature

δθX为仪器传感器及电路部分的综合温度系数，是一个需要预估的变量。ΔtX是测量偏角D前后的环境温度差。则偏移量均值为

此时需要引入一个理论上的真实值ΣΔSXT/4，则

2.3 修正系数的影响

对于修正系数CX，其通过每年1次的仪器标定得出，每次标定结果的误差以标准偏差来表示。通常情况下，比测与标定相隔数月，修正系数已发生了变化，这种变化对于日常的磁场测量，影响可忽略不计，但对于更高指标要求的仪器比测，则必须加以考虑，因此，若采用上次标定的修正系数进行计算，则

式中，CT是引入的测量时的真实修正系数，δCX为误差。图4为乾陵地磁台Mingeo型磁通门经纬仪修正系数自2015年以来的变化。

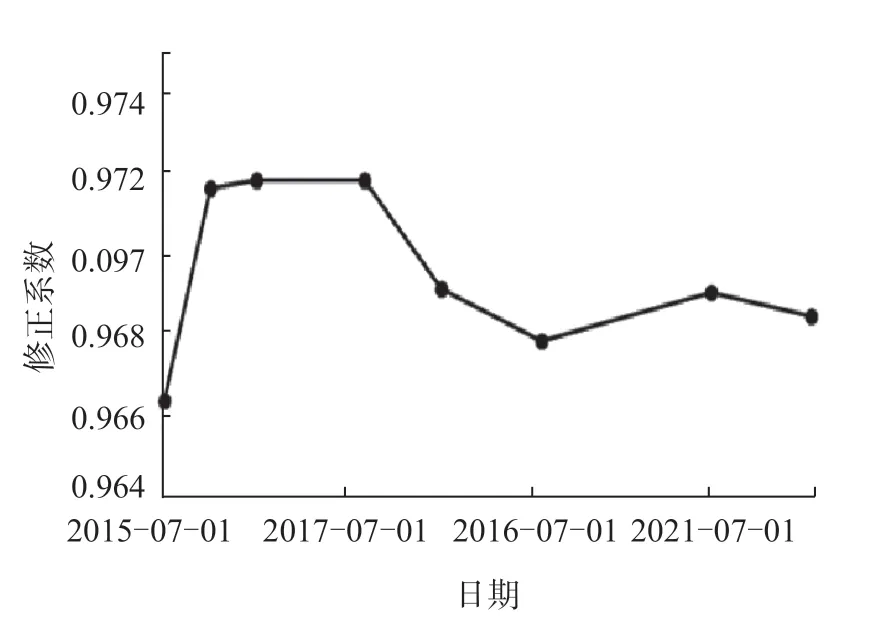
图4 修正系数的变化Fig.4 Changes incorrection coefficient

2.4 修正值误差ε的计算

综上，设重复测量N次取平均值，则式（5）替换为

式（5）中αDX为实测的修正值，为了分离出真实修正值部分，结合式（8）、式（9），得

同理，计算可得标准仪器及倾角I的修正值误差。

3 建立新的比测模型

N次测量所得被测仪基线值均值包含修正值αDX，从而DX包 含(误BX差标(准仪器)同样如此。比测过程中消除了以上各项误差的磁偏角D的仪器差EDX，计算模型（近零法）为

同样得到磁倾角I的仪器差（近零法）为

4 实验验证

4.1 不确定度的评定

依托新的比测模型，采用GUM 法对仪器差EDX、EIX进行测量不确定度的评定。由于式（13）、式（14）的比测模型为非线性，根据《JJF 1059.1—2012 测量不确定度评定与表示》（中华人民共和国国家质量监督检验检疫总局，2013），合成标准不确定度应采用下式继而计算出各输入量的标准不确定度u(xi)、灵敏系数ci以及合成不确定度uc。

依照上述方法，以某地磁台的一次磁通门经纬仪比测数据进行计算（近零法，量值溯源至国内基准），各变量估计范围及测量原始参数见表1。

表1 D、I测量原始参数Table 1 Original parameters for the D、I measurement

对各输入量的分布进行估计，继而得到各不确定度分量，见表2、表3。

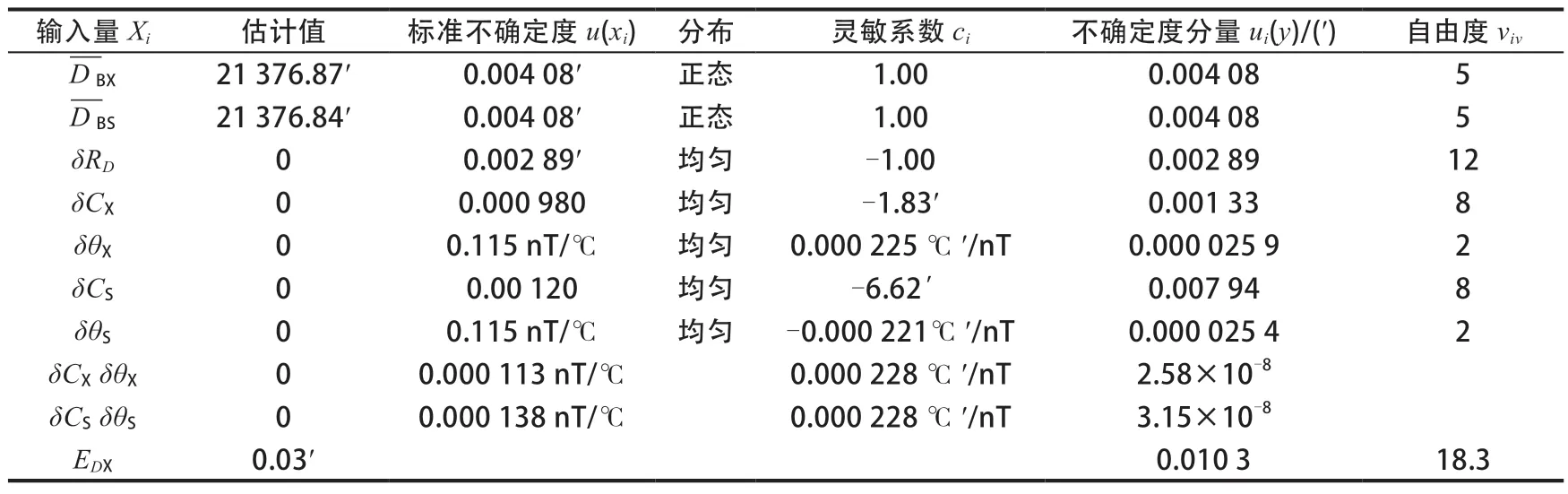
表2 某DI仪磁偏角（D）测量值校准的不确定度分量汇总Table 2 Uncertainty components for calibration of the magnetic declination (D) measurement of a DI instrument

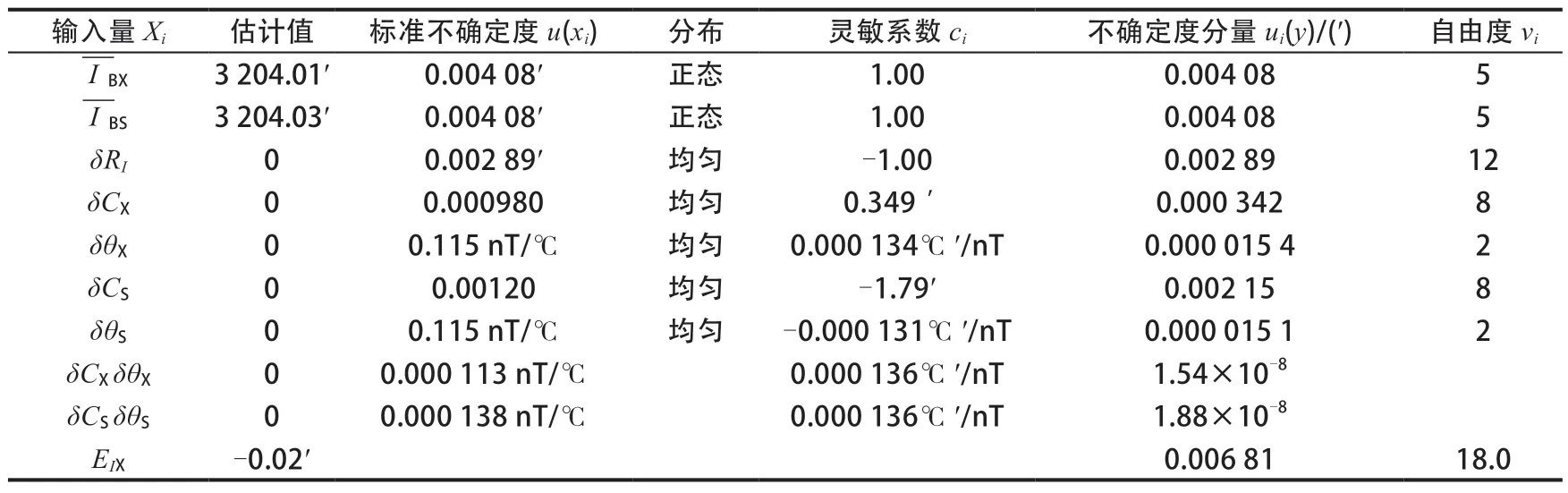
表3 某DI仪磁偏角（I）测量值校准的不确定度分量汇总Table 3 Uncertainty components for calibration of the magnetic inclination (I) measurement of a DI instrument

EDX、EIX的标准不确定度uc(EDX)=0.0103′，uc(EDX)=0.00681′。EDX、EIX接近于正态分布，取k=2，则EDX、EIX的扩展不确定度

最终，该仪器的仪器差

依据该结果，对被测仪器的仪器差进行合格性判定，MPE=0.1′。

如图5所示，2项结果都合格，显然这种表示和判定方法更可信，也与该仪器多年的比测结果相符合。

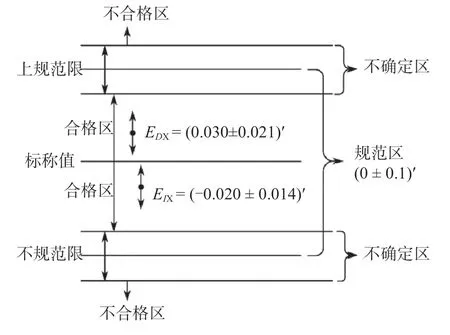
图5 符合性判定的区域Fig.5 Area for compliance determination

4.2 与传统方法的比较

参考新的模型，使用2019年全国基准地磁台网比测的部分仪器测试数据（非最终结果，部分仪器进行了复测）进行不确定度评定并重新判定结果，所列结果多数在最大允许误差（MPE=0.1′）附近，误判的可能性较大，结果如表4。

表4 仪器差判定结果对比Table 4 Comparison of instrument difference determination results

按新的方法对12项结果判定后，有8项改判为“待定”，改判率达到67%，说明原判定结果存疑，需要谨慎对待，同时评定过程明确了问题所在，可针对性的查找原因，将系统因素的影响降到最低。例如乌加河的EDX=-0.04′，虽数值较小，但由于系统原因，其测量不确定度达到了0.069′，结果由合格变为待定。在新方法的评定中的标准不确定度分量达到0.033′，占比最大，而日变、温度、修正系数等引入的不确定度分量都小于0.01′，可排除这些因素，剩余因素则为测量错误，如仪器定位调平错误、标志观测错误等，或仪器故障，其影响则对应于的标准不确定度分量，这也与实际经验相符。因此可直接对测量过程进行核查并复测，若结果不变，则说明仪器故障，可认定不合格。而根据原方法和结果，无法直接做出以上判断，须对所有系统因素逐一核查、多次测量后确定是否为测量错误导致。喀什台的前后判定结果保持了一致，说明原结果不仅未超限，且各系统因素的影响也不足以改变判定。相比之下，新的比测模型对结果的判定更加科学和谨慎，减少了误判的发生。

5 结论

本研究建立了包含多种系统因素的、基于近零法和指零法的磁通门经纬仪比测模型，依托该模型，采用GUM方法，通过实际数据进行了测量不确定度评定实验，相比于传统比测模型和判定方法，结果表明：

（1）新的模型更加符合实际，依据该模型进行测量不确定度评定后，改进了结果的表示形式，优化了判定结果，该模型可以作为传统模型的替代。

（2）根据新模型的公式及不确定度的评定过程，得出了抑制测量过程中系统影响因素的方法：①测量次数N应控制在最佳范围内，N过小导致随机误差增大；若N过大，虽然随机误差减小，但延长了测量时间，导致相对记录仪日变、人员精力下降以及其它环境因素变化引起的不确定度上升。②因日变δR的不确定度对结果影响较大，所以应当科学合理地架设相对仪器，使其达到Z轴最佳的垂直度和最佳定向状态，并根据仪器的日变曲线选择日变化最小的时段进行测量工作。③控制标准仪器修正系数的变化量δC的范围，需要对仪器进行长期的观察，可以通过绘制长期的修正系数变化图来把握其变化规律，如果每年能增加标定次数，则更细化的变化规律有利于缩小变化量范围。④对于标准仪器，温度系数取值范围的确定需要测量员对仪器有所了解，或通过试验测得。对于被测仪器，无法进行试验，温度系数取值范围较难把握，但根据模型计算，温度系数引入的相关不确定度的灵敏系数c会随着ΔtX减小而以2倍数量级的速度减小，因此只要对观测室温差加以控制，温度系数引入的不确定度分量就将明显减小，甚至可忽略。