时空需求下的电动汽车充电设施选址优化模型

周筝 龙华 李帅 梁昌侯

摘 要：针对电动汽车充电站布局位置不合理、充电利用率较低等问题，提出了一种时空需求下的充电设施选址优化模型STDM。通过对电动汽车出行数据的时空分布特征进行挖掘，结合电动汽车的出行与充电行为构建充电需求预测模型来获得区域内时空需求分布；采用基于时空统计量的方法获取需求热点区域，考虑到充电站服务覆盖问题，定义充电覆盖率作为模型评估参数；在此基础上从用户角度与运营和社会角度综合构建电动汽车到站距离成本、充电站建设运行成本和碳排放成本的优化模型。最后通过实际数据验证模型的可行性和有效性。结果表明，模型得出了区域内12个充电站的选址方案降低综合成本，同时确定充电站的布局位置与充电桩数量；此外，采用所提方法得到的模型选址结果相比于其他文献方法能够有效缩短电动汽车到站距离，并提高到站覆盖率。

关键词：电动汽车； 充电站选址； 布局优化； 需求热点； 时空分布

中图分类号：U491;TM73   文献标志码：A

文章编号：1001-3695（2023）09-011-0000-00

doi：10.19734/j.issn.1001-3695.2023.02.0035

Optimization model for location of electric vehicle charging station under

spatial-temporal demand

Zhou Zheng， Long Hua， Li Shuai， Liang Changhou

（Faculty of Information Engineering & Automation， Kunming University of Science & Technology， Kunming 650500， China）

Abstract：For the problems of unreasonable layout location and low charging utilization rate of EV charging stations， this paper proposed a spatial-temporal demand model （STDM） for location optimization of charging stations under spatial-temporal demand. By mining the spatial-temporal distribution characteristics of EV travel data and combining the travel and charging behaviors of EVs， it built a charging demand prediction model to obtain the spatial-temporal demand distribution in the region. The method based on spatial-temporal statistics obtained the demand hotspot areas， and the charging coverage rate as the model evaluation parameter considered the service coverage of charging stations. A comprehensive model included the perspectives of users， operators and society with EV distance cost to the station， charging station construction and operation cost and carbon emission cost. Finally， simulation results based on actual data show the feasibility and validity of the model. The results show that the model has set up 12 charging stations in the region to reduce the comprehensive cost， while determining the layout location and the number of charging piles. The optimization model results effectively reduce the EV arrival distance and improve the arrival coverage compared with other methods.

Key words：electric vehicle（EV）; charging station location; layout optimization; demand hotspots; spatial-temporal distribution

0 引言

目前，交通運输部门产生的石油能源需求占全球石油消费的70%以上，其二氧化碳等温室气体排放量占比超过20%［1］，道路交通运输的能源消耗与温室气体排放带来的环境污染问题逐渐引起人们的重视。电动汽车（EV）与油耗汽车相比在节能减排方面具有巨大优势［2］，其推广与使用能够应对目前石油能源的供应风险和环境气候污染带来的挑战［3］。然而，国内在电动汽车充电基础设施建设和产业规模效益等方面与国外相比仍有一定的差距，电动汽车发展目前仍存在诸多阻碍。公共充电设施的分布不合理、较长充电时间与有限电池容量等问题所带来的里程焦虑仍是限制电动汽车需求发展的主要原因之一［4，5］，而充电基础设施布局的科学性与合理性能够更好地为EV用户提供充电服务，挖掘潜在市场［6］。

现阶段充电站选址优化的研究大多采用目标规划的方式求解，以成本最小化和效益最大化作为目标函数，同时采用仿真模拟或数据驱动的方式表示研究区域内充电需求，从而建立单目标或多目标规划模型来优化充电站布局。在目标函数的选取上，考虑经济效益时以充电站建设［7，8］、运营成本最小化为目标［9，10］，同时还有行驶距离［11］、时间成本［12］等。苏粟等人［9］通过挖掘起讫点分布特征来综合构建以站点建设成本和相应时间成本为目标函数的规划模型。Narges等人［11］建立以车辆行驶里程最大化为目标，构建混合整数线性规划模型优化站点选址。Qu等人［12］利用GIS分析研究交通网络特征，建立以用户和充电站成本最小化为目标的三阶段选址模型并通过遗传算法求解。针对选址模型中的集合覆盖问题［13］，叶臻等人［14］采用核密度估计法，以服务需求覆盖最大化为目标构建了车辆服务站选址模型。

由于EV出行通常会根据日常出行需求呈現出一定的规律性，在布局优化过程中，模拟分析EV出行与充电行为同样重要［15］，这也是城市交通拥堵和热点区形成的重要原因之一［16］。Dominguez等人［17］采用蒙特卡罗方法对充电需求进行模拟，建立了电动汽车到达和充电过程模型。葛少云等人［18］提出充电站点选择的效用函数，结合效用极大原理研究车辆行为特性和需求分布。以上文献对电动汽车行为和充电需求是在概率模型的基础上，采用蒙特卡罗等方法进行模拟，缺少真实数据的支撑，且无法准确获得电动汽车出行充电需求的时空信息。针对此问题，Justine等人［19］通过佛蒙特州充电站案例研究用户出行行为来预测充电需求。Tu等人［20］从大量GPS数据中提取车辆的时空需求，利用电动汽车的时空需求和车辆与充电站之间的交互行为构建了定位模型来最大化充电服务水平。Hu等人［15］从GPS数据中提取轨迹与子轨迹集，将研究区域离散网格化并以网格单位识别充电出行需求。Xiao等人［16］构造轨迹相似度矩阵，利用核主成分分析法描述用户出行行为并提取出行规律。为了更好地描述电动汽车出行需求热点，现有研究大多采用聚类算法进行挖掘。Hung等人［21］将充电站布局问题简化成路由问题，通过规模约束的聚类方法进行选址。王妍等人［22］采用谱聚类方法对电动汽车出行行为进行快速聚类从而规划选址目标。张艺涵等人［23］提出了基于最大轮廓系数的密度峰值聚类方法获取充电需求的空间分布。任峰等人［24］采用k-means算法来分析电动汽车的常驻点集群。罗思杰等人［25］采用基于密度的聚类方法选取停留密集区域作为充电站位置。

综合上述文献，现有研究采用基于聚类算法的热点挖掘分析充电需求分布，同时建立目标规划模型进行充电站选址优化。但考虑到上述研究挖掘充电需求分布时大多以空间维度为主，容易忽略时间维度与空间上的低密度区域，且在空间轨迹数据分布不均时难以确定Eps半径参数或类的数目［26］。同时，电动汽车社会经济效益中存在碳排放问题会对社会经济成本目标产生一定的影响。因此，本文在借鉴现有研究的基础上，提出一种时空需求下的充电设施选址优化模型STDM，采用基于时空统计量的方法挖掘研究范围内潜在的电动汽车充电时空需求热点区域，并以到站成本、碳排放成本和建站成本为目标函数优化站点位置和数量，旨在降低综合成本并优化充电服务水平，提高充电站建设的合理性。同时以某地中心城区的电动汽车时空数据为例进行实验分析，验证所提模型的可行性与有效性。

1 电动汽车充电需求与成本模型

1.1 充电需求预测模型

EV用户在出行过程中具有随机性，因此会产生具有不确定性的充电需求，为模拟EV行驶特性首先需要对其充电需求进行研究。根据文献［27］对EV用户首次出行下初始电量统计数据的估计与拟合结果，本文定义首次出行时的荷电状态（state of charge，SOC）服从正态分布N（μ，σ），概率密度函数如式（1）（2）所示。

f（SOCinit，μ，σ）=1σ2πexp－（SOCinit－μ）22σ2（1）

Br=SOCinit×BC（2）

其中：μ和σ为估计均值和标准差，μ=0.8，σ=0.1［28］;SOCinit为初始荷电状态;BC为电池容量;Br为EV出行前的初始电量。设置EV单位里程能耗为Ec，从hs到达hd的行驶距离为m（hs，hd），则完成一次出行后的电量ΔE如式（3）所示。

ΔE=Br－m（hs，hd）Ec，ΔE>0（3）

根据处理后的数据集进行分析，模拟EV出行的耗电过程，并设计算法建立充电需求预测模型。具体过程如下：假设EV在某一时间域中的起始位置为his=（x1，y1），终止位置hid=（xn，yn），那么该时间域内第i个EV从起始位置到终止位置之间行驶的轨迹集合Hi可表示为Hi={his，hi1，hi2，…，hid}，其对应时序集TiH可表示为TiH={Tis，Ti1，Ti2，…，Tid}，其中Tis和Tid表示从his到hid的起始时间和终止时间。首先提取i辆EV的轨迹集Hi中首次出行对应的位置和时间（his，Tis），然后根据式（1）获得EV初始SOC值。本文设置EV产生充电需求时的SOC阈值为40％，EV用户在结束本次行程时，若在进行下一行程结束时剩余电量Br无法支撑EV到达最近的充电站，即Br≤m（hs，hd）Ec，则判断本次行程结束时EV存在充电需求，记录此时该电动汽车i在时刻Tij的位置hij和剩余电量ΔE。

1.2 碳排放模型

EV在行驶途中采用电能以替代传统化石燃料，达到使用过程中的零排放，而将碳排放过程转移到车辆生产、发电和充电等环节中［29］。因此EV使用的电能在发电环节同样会产生碳排放问题，但远小于油耗车在使用过程中产生的排放量。合理的充电站布局能够减少EV不必要的出行能耗，从而降低碳排放量，提高社会效益。为研究EV使用电能的碳排放对充电站选址布局的影响，在考虑研究区域内车辆总量、出行里程、单位距离能耗等基础上，采用燃料生命周期碳排放计算方法［30］来研究其使用电能的碳排放量CE，如式（4）所示。

CE=∑i∈I∑t∈Tmt（his，hid）×Ec×θξce×ξte×1244（4）

其中：mt（his，hid）为研究区域内电动汽车i在时刻t的出行距离，计算研究区域下总时间段内所有汽车的行驶距离，单位为km；ξce和ξte为车辆充电效率与输电效率，文中均取90%；θ为EV使用电能单位千瓦时下二氧化碳排放系数，单位t·（kW·h）－1。

1.3 充电站基础设施成本

充电站基础设施成本包括充电站建设运营成本、充电设备成本和折旧成本［7］。其中建设运营成本包括土地成本、配电网设施、消防安全以及建筑和道路建设等前期投资费用，还有运营后聘请人员、维护设施等运营费用；充电设备成本包括充电设施的购买与安装成本。设决策变量Ku={0，1}用于描述充电站在位置u处建设情况，Ku=1表示在位置u处建立充电站。则充电站建设运营成本Pconstruction如式（5）所示，充电设备成本Pdevice如式（6）所示，p1为建站单位成本，p2为设备单位成本，su为充电设备个数。

Pconstruction= ∑u∈Up1Ku（5）

Pdevice=∑u∈Up2suKu（6）

考虑到充电设备使用存在基础寿命ts，定义充电设备以折现率τ逐年折旧［7］，则充电站总建设成本Pstation如式（7）所示。

Pstation= τ（1+τ）ts（1+τ）ts－1（Pconstruction+Pdevice）（7）

1.4 评估方法

充电站布局需尽可能提高其充电服务水平，从而最大限度满足EV充电需求。当EV在时间Tij和位置hij时，到达距离最近的充电站的距离mi包含在充电站服务半径z内，此时EV为被覆盖的状态。因此，关于区域内充电站选址布局问题可用充电到站的最大覆盖程度来描述。为评估模型的有效性，定义充电站最大覆盖率参数作为模型评估指标，对于车辆i∈I，其覆盖情况如式（8）所示。

ε=∑Ii=1αiN（8）

αi=1 mi≤z

0 mi>z

（9）

其中：ε為覆盖率，N为研究范围内EV出行和停留的事件总数，αi为二进制变量，如式（9）所示，当车辆到达最近的充电站距离小于服务半径z时取αi=1；否则αi=0。

2 时空需求下充电设施选址优化

2.1 车辆需求热点区域获取

时空扫描统计量是一种挖掘时空数据的方法，在扫描过程中根据扫描窗口内外对象的统计差异性来探测研究区域内任意时段下事件点的集中度高于外部的区域，即挖掘具有统计意义的热点聚集区域，同时寻找需求分布较高的潜在区域，从而能够在一定程度上提高充电服务水平。相比基于层次和基于密度的聚类方法，时空扫描基于统计原理能够结合时间与空间两种维度信息挖掘聚类热点区域的同时，用显著性水平来衡量不同热点之间的重要性差异程度，并对低密度区域同样进行统计监测，在检测圆形热点方面具有较高的准确性水平［31］。其中，该方法在平面上以圆形等作为空间上的扫描窗口，并引入窗口高度形成圆柱形窗口来描述时间维度。如图1所示，研究区域内以（x，y）为中心点，z为平面空间域扫描窗口半径，T为时间域扫描窗口高度，通过移动扫描窗口直至所有空间域内时间单元扫描完成为止。

对于EV研究对象，定义其出行概率服从泊松分布［32］，将时间段T按天数划分为多个时间段T={T1，…，Tj，…}，则Tj时刻区域h内包括EV出行和停留的事件总数量N如式（10）所示。

N=∑h∈H∑t∈Tni，t（10）

其中：ni，t表示在t时间段下区域h处的EV数量。采用图1中的圆柱体窗口对研究区域进行遍历扫描以获取统计量，并用对数广义似然比来衡量区域内的聚集性，如式（11）所示。对数似然比越大，表示范围内的聚集程度越高，覆盖区域即为可能性较高的聚集区域MLC（most likely cluster）。

LLRG=NGlnNGγG+（N－NG）lnN－NGN－γG×f（NG>γG）（11）

其中：NG表示扫描区域G内EV实际数量，γG表示期望数量；f（NG>γG）为指示函数，当EV实际数量大于期望值时f（NG>γG）=1。获得统计量最大的聚集区域后，通过蒙特卡罗方法获取仿真数据以模拟假设检验过程，验证范围内的分布规律，并确定聚集程度最高的显著性区域。

考虑到部分聚集区域中心可能存在距离相近或覆盖范围大幅度重叠的状况，站点位置选择在兼顾需求热点的同时，站间距应控制一定距离，且实际建设中存在成本问题，因此引入半径约束，对相距较近的聚集区域求取其中心点作为选择站点，假设待优化站点位置集cs中经纬度坐标点为（xj，yj），则在半径约束下优化后的聚集中心点坐标（x′j，y′j）如式（12）和（13）所示，其中（xωj，yωj）为弧度坐标。

x′j=arctan∑nj=1sinxωjcosyωj∑nj=1cosxωjcosyωj（12）

y′j=arctan∑nj=1sinyωj∑nj=1sinxωjcosyωj2+∑nj=1cosxωjcosyωj2（13）

2.2 目标函数

本文提出的STDM旨在研究范围内寻找充电需求热点位置，并结合目标函数优化来降低充电站建设的综合成本，同时最大限度提高用户充电的服务水平，进一步提高布局合理性。充电站布局位置优化能够尽可能减少EV用户到站距离，并增加出行总距离。到站距离越短、出行总距离越长说明服务水平越高。考虑到实际中建站成本问题，随着充电站数量的增多其充电服务覆盖范围随之扩大，EV到站距离越小，但充电站数量应控制在一定范围内以减少充电站建设成本，也在一定程度上优化资源分配。同时，EV在使用过程中能够代替油耗车实现碳减排的目标，而发电过程的碳排放同样作为EV使用成本的一部分。综上所述，结合式（4）和（7）的成本模型得到STDM的目标函数如式（14）（15）所示。

min β1η1∑i∈I∑u∈U∑hu∈Hmi（hs，hu）XiuYu+η2CE+β2Pstation（14）

s.t. Br－Ec（hs，hd）>Ec（hd，hu）Xiu=1

Br－Ec（hs，hd）≤Ec（hd，hu）Xiu=0（15）

式（14）中：I为EV集合;H为EV出行轨迹集合;U为备选站点集合;mi（hs，hu）表示第i輛EV从起始位置hs到充电站u的距离;η1和η2分别为出行距离成本和碳排放成本系数，引入成本系数将出行距离与碳排放量转换为经济成本;考虑到充电站社会公共服务功能制定权重系数β1与β2，其取值分别为β1=1.2，β2=0.8［8］。式（15）中Xiu为能耗约束，表示EV剩余电量为Br时，在下次出行结束后剩余电量足以支撑EV到达最近充电站，则视为满足出行需求且Xiu=1；Yu为充电站选择变量，当EV选择充电站u时Yu=1，否则Yu=0。

2.3 模型求解流程

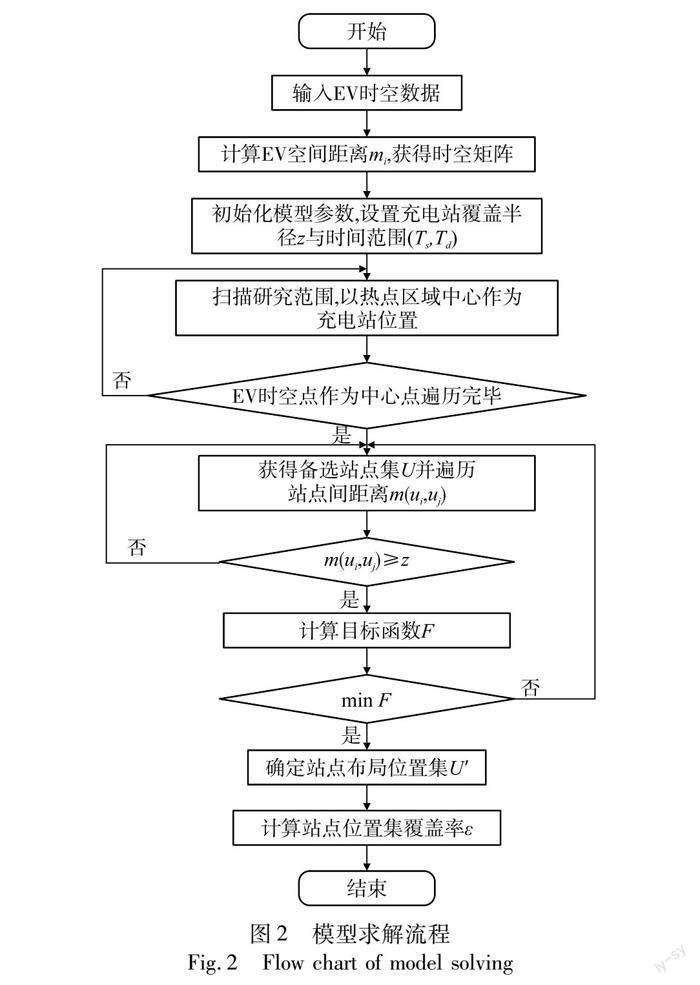
在结合充电需求热点区域获取方法和成本目标函数后，得到模型求解流程如图2所示。

a）输入处理后的EV时空数据{GRIDi，Hi，TiH，Biinit}，包括EV轨迹位置点集合Hi，车辆i当前位置点的网格编号GRIDi，时间戳TiH和当前时刻SOC值Biinit。计算EV位置点之间的空间距离mi，获得时空矩阵。

b）初始化模型参数。设置充电站覆盖半径z和扫描时间范围（Ts，Td），通过时空扫描统计量方法遍历研究区域以获取热点中心，作为充电站备选位置，遍历完毕后获得充电站备选站点集合U。随后引入半径约束m（ui，uj）≥z，对于不满足约束的站点位置根据式（12）（13）计算以合并获得新的位置，并更新集合站点集U，直至集合U遍历完毕。

c）根据目标函数和约束条件。结合综合成本模型式（14）计算目标函数值，以最小化minF为目标寻求模型最优解，得到充电站布局的位置集U′。

d）根据式（8）（9）计算以U′为充电站布局的情况下研究区域内所有EV时空点的覆盖率ε作为模型评价指标，同时返回U′中站点的网格编号和经纬度位置点。

3 实验分析

3.1 数据集与模型参数

本文数据集使用2018.12.11—2019.1.10特拉维夫市电动汽车定位数据进行实验，模型算法采用Python 3.7编写。原始数据集为共260辆EV在时间范围内的共计一百万余条定位数据，数据包括时间、空间以及车辆编号ID字段。在进行预处理删去重复、缺失数据和异常值等后提取有效数据约六十万余例，随后根据EV停留和移动行为共提取37 144例出行数据，充电需求1 600例。考虑到EV出行具有时间和空间两个维度的特征，因此将数据集划分为以ID作为关联的时间数据和空间位置点两部分。其中空间数据进行网格化处理，得到研究区域内146个网格点，如表1所示，时间维度特征按天为单位处理，统计在相同网格点内的EV数量，如表2所示，表中ID字段为未网格化时对应的经纬度位置点编号。

模型参数设置时空扫描统计量的起始时间Ts为2018.12.11，结束时间Td为2018.12.18，扫描区域作为充电站覆盖半径z，设置z=2 km，所有EV的电池容量BC相同，均为60 kW·h。充电站建设成本p1为10万元，设备成本p2为10 000元/台，折现率0.1，折旧年限10年；碳排放成本1 000元/t，EV城市出行单位距离成本20元/km。

3.2 电动汽车出行提取与充电需求分布

以研究区域的EV时空数据为例，对提取后的37 144例出行数据以案例点的形式在地图上表示，如图3所示。考虑到EV出行过程中存在充电需求，采用充电需求预测方法来模拟EV的充电需求分布情况，其中时间维度上分布情况如图4所示。从图4中可看出EV充电需求数量于7：00～8：00、15：00～18：00时间范围内达到高峰期。以天为单位统计研究时间范围内各个位置点的EV数量，得到充电需求的空间分布如图5所示。

3.3 充电设施选址优化

设置研究区域内各个充电站的充电桩数范围为10～50个。采用STDM模型优化充电站布局位置和数量，则考虑建站成本、到站距离成本和出行碳排放成本的综合成本如图6所示。

从图6中可看出，随着充电站数量的增加，综合成本整体呈现上升的趋势。其中充电站个数为Nu=12此时目标值呈现下降趋势且综合成本最低，为5 729万元。为描述Nu=12时充电服务覆盖能力，选取充电站数量8～16个，计算不同充电站数量下z=1 km时的充电服务覆盖率，如图7所示。从图7中可看出充电站数量从到Nu=12时服务覆盖率的变化幅度较大，之后随着站点数量的增加变化幅度减少，呈缓慢增长趋势。这说明当区域内设置12个充电站时能够更为充分地利用各个充电设施。因此，得到区域内充电站最优数量为12个，此时在避免建设过多充电站导致资源浪费的同时，能够有效减少建站综合成本，并提高EV充电服务覆盖水平。各个充电站的位置和充电设施信息如表3所示。

3.4 模型效果评估

研究范围内充电站布局数量以20个为例，对数据集进行  划分，时间范围选取2018.12.11—2019.1.8期间作为选址数

据，并采用模型评估参数进行验证。本文方法即时空需求下的充电站选址模型STDM，文献［22，24］分别采用谱聚类和k-means方法进行选址，文献［25］采用基于密度的DBSCAN聚类方法进行选址，仿真结果如表4所示。

表4中均包含选址经纬度位置和时间范围内的当前站点EV充电停留的总数量。从表4中可看出本文方法下EV到站充电数量最多为序号9的242例，最少为序号14的30例；文献［22］下EV到站充电数量最多为序号13的285例，最少为序号16的14例；文献［24］下EV到站充电数量最多为序号7的349例，最少为序号5的9例；文献［25］下EV到站充电数量最多为序号17的200例，最少为序号7的8例。通过对比分析可知，本文模型能够更好地挖掘研究区域内时空维度下的充电需求热点，并且给定选址位置能够相对均衡充电需求的到站分布，在挖掘充电需求热点的同时兼顾需求较低的冷点区域，从而提高充电设施的利用。

为进一步验证本文模型的有效性，将研究时间范围划分为2018.12.11—2018.12.18、2018.12.21—2018.12.28和2019.1.1—2019.1.8三组数据进行实验，计算不同方法下的到站距离和不同服务半径下的覆盖率，结果如表5所示。

从表5中可看出，相比于其他文献方法本文方法能够有效缩短EV到站距离，并提高不同服务半径下的覆盖率。其中，EV到站距离相比文献［22，24，25］显著减少，平均缩短了29.1%、39.58%和11.5%；服务半径为1 km和2 km时本文所提方法的覆盖率相较其他文獻均有所提高，说明本文方法能够更好地获取区域内需求热点；同时，服务半径为3 km时覆盖率基本能够实现EV到站服务。由此可见本文方法的覆盖率整体有所提高，说明所提模型STDM能够在缩短到站距离的同时，能够较好地提高EV到达充电站的可达性。

4 结束语

本文提出了一种时空需求下的电动汽车充电设施选址优化模型。首先，基于EV的GPS出行数据提取时空分布特征，结合其出行与充电的特点建立充电需求预测模型，获得区域内EV的充电需求在时间和空间上的分布情况；接着采用基于时空统计量的方法挖掘需求热点区域作为备选站点，引入服务覆盖半径做站间约束，定义充电服务覆盖率作为评估参数；同时在考虑用户侧、运营侧和社会侧三种效益成本下构建综合成本目标优化模型，旨在降低综合成本的目标下进行站点数量与成本间的敏感性分析实验，确定研究区域内最优充电站选址布局。最后，以EV到站距离和充电服务覆盖率作为评估参数进行对比实验，验证模型的有效性。得出结论如下：

结合算例数据，根据充电需求预测模型得到EV需求共1 600例，综合来看于7：00—8：00、15：00—18：00达到高峰期；研究区域下设置12个充电站时综合成本最低，为5 729万元，此时站点与服务设施数量和布局设置能够在提高设施利用率的基础上降低用户成本和碳排放成本，避免建设过多充电站导致资源浪费。此外，本文方法与其他文献对比可看出能够有效缩短EV到站距离并提高充电服务覆盖率，验证了模型的可行性和有效性。

电动汽车出行对交通网络产生影响的同时，其充电过程还会影响充电站点负载情况。后续研究将以充电过程的负载均衡为目标，在考虑EV充电时空需求的基础上，预测充电负载并优化不同站点内部的充电服务设施数量，从而研究在满足充电需求的基础上引导EV充电服务来实现充电站负载均衡问题。

参考文献：

[1]Tan Xiaoqi，Sun Bo，Wu Yuan，et al.Asymptotic performance evaluation of battery swapping and charging station for electric-vehicles［J］.Performance Evaluation，2018，119：43-57.

［2]梁士栋，赵勍，何建佳，等.共享充电桩下负荷时间分布均衡的小区电动汽车充电方案优化［J］.计算机应用研究，2022，39（12）：3688-3693，3700.（Liang Shidong，Zhao Qing，He Jianjia，et al.Optimization of community electric vehicle charging schemes with balanced load time distribution under shared charging hubs［J］.Application Research of Computers，2022，39（12）：3688-3693，3700.）

［3]罗佳欣，何登旭.基于改进郊狼优化算法的充电站选址定容规划［J］.计算机应用研究，2022，39（3）：751-757.（Luo Jiaxin，He Dengxu.Site selection and capacity planning of charging station based on improved coyote optimization algorithm［J］.Application Research of Computers，2022，39（3）：751-757.）

［4]Huber G，Bogenberger K，Van L H.Optimization of charging strategies for battery electric vehicles under uncertainty［J］.Trans on Intelligent Transportation Systems，2022，23（2）：760-776.

［5]Baum M，Dibbelt J，Wagner D，et al.Modeling and engineering constrained shortest path algorithms for battery electric vehicles［J］.Transportation Science，2020，54（6）：1571-1600.

［6]Rauh N，Franke T，Krems J.User experience with electric vehicles while driving in a critical range situation：a qualitative approach［J］.Institution of Engineering and Technology Intelligent Transport Systems，2015，9（7）：734-739.

［7]Xiao Dan，An Shi，Cai Hua，et al.An optimization model for electric vehicle charging infrastructure planning considering queuing behavior with finite queue length［J］.The Journal of Energy Storage，2020，29：101317.

［8]姜欣，冯永涛，熊虎，等.基于出行概率矩阵的电动汽车充电站规划［J］.电工技术学报，2019，34（S1）：272-281.（Jiang Xin，Feng Yongtao，Xiong Hu，et al.Electric vehicle charging station planning based on trip probability matrix［J］.Journal of Electrical Technology，2019，34（S1）：272-281.）

［9]苏粟，李玉璟，贾泽瑞，等.基于GPS轨迹挖掘的电动出租车充电站规划［J］.电力自动化设备，2022，42（10）：255-263.（Su Su，Li Yujing，Jia Zerui，et al.Electric taxi charging station planning based on GPS trajectory mining［J］.Power Automation Equipment，2022，42（10）：255-263.）

［10]Asamer J，Reinthaler M，Ruthmair M，et al.Optimizing charging station locations for urban taxi providers［J］.Transportation Research Part A：Policy and Practice，2016，85：233-246.

［11]Narges S，Hua Cai，Metin T，et al.Optimal locations of electric public charging stations using real world vehicle travel patterns［J］.Transportation Research Part D：Transport and Environment，2015，41：165-176.

［12]Qu Zhaowei，Wang Xin，Song Xianmin，et al.Location optimization for urban taxi stands based on taxi GPS trajectory big data［J］.IEEE Access，2019，7：62273-62283.

［13]孙智勇，宁爱兵，傅汤毅，等.最小费用充电站选址问题的分支定界算法［J］.计算机应用研究，2022，39（1）：80-83.（Sun Zhiyong，Ning Aibing，Fu Tangyi，et al.Branch and bound algorithm for minimum cost charging station location problem［J］.Application Research of Computers，2022，39（1）：80-83.）

［14]叶臻，贺明光，梁科科.基于服务需求的出租汽车服务站选址方法［J］.重庆交通大学学报：自然科学版，2019，38（3）：75-82，109.（Ye Zhen，He Mingguang，Liang Keke.Location method of taxi service station based on service demand［J］.Journal of Chongqing Jiaotong University：Natural Science，2019，38（3）：75-82，109.）

［15]Hu Dandan，Huang Lyu，Lyu Chen，et al.Data driven optimization for electric vehicle charging station locating and sizing with charging satisfaction consideration in urban areas［J］.Institution of Engineering and Technology Renewable Power Generation，2022，16（12）：2630-2643.

［16]Xiao Zhu，Xu Shenyuan，Li Tao，et al.On extracting regular travel behavior of private cars based on trajectory data analysis［J］.IEEE Trans on Vehicular Technology，2020，69（12）：14537-14549.

［17]Dominguez N J，Dufo L R，Yusta L J，et al.Design of an electric vehicle fast charging station with integration of renewable energy and storage systems［J］.International Journal of Electrical Power and Energy Systems，2019，105：46-58.

［18]葛少云，李榮，韩俊，等.考虑电动出租车随机概率行为特性的充电站规划［J］.电力系统自动化，2016，40（4）：50-58.（Ge Shaoyun，Li Rong，Han Jun，et al.Charging station planning considering random probabilistic behavior characteristics of electric taxi［J］.Power System Automation，2016，40（4）：50-58.）

［19]Sears J，Glitman K，Roberts D.Forecasting demand of public electric vehicle charging infrastructure［C］//Proc of IEEE Conference on Technologies for Sustainability.Piscataway，NJ：IEEE Press，2014：250-254.

［20]Tu Wei，Li Qingquan，Fang Zhixiang，et al.Optimizing the locations of electric taxi charging stations：a spatial–temporal demand coverage approach［J］.Transportation Research Part C：Emerging Technologies，2016，65：172-189.

［21]Hung Yingchao，Michailidis G.A novel data-driven approach for solving the electric vehicle charging station location-routing problem［J］.IEEE Trans on Intelligent Transportation Systems，2022，23（12）：23858-23868.

［22]王妍，吳传申，高山.基于电动汽车行驶数据快速聚类的充电站选址优化［J］.电力需求侧管理，2021，23（3）：8-12.（Wang Yan，Wu Chuansheng，Gao Shan.Site selection optimization of charging station based on rapid clustering of electric vehicle driving data［J］.Power Demand Side Management，2021，23（3）：8-12.）

［23]张艺涵，徐菁，李秋燕，等.基于密度峰值聚类的电动汽车充电站选址定容方法［J］.电力系统保护与控制，2021，49（5）：132-139.（Zhang Yihan，Xu Jing，Li Qiuyan，et al.Location and capacity determination method of electric vehicle charging station based on density peak clustering［J］.Power System Protection and Control，2021，49（5）：132-139.）

［24]任峰，向月，雷小林，等.基于GPS数据的电动出租车充电桩选址定容［J］.电力自动化设备，2022，42（10）：273-279.（Ren Feng，Xiang Yue，Lei Xiaolin，et al.Location and capacity determination of electric taxi charging pile based on GPS data［J］.Electric Power Automation Equipment，2022，42（10）：273-279.）

［25]罗思杰，邹复民，郭峰，等.基于轨迹数据的出租车充电站选址方法［J］.计算机工程与应用，2022，58（8）：273-282.（Luo Sijie，Zou Fumin，Guo Feng，et al.Location method of taxi charging station based on trajectory data［J］.Computer Engineering and Applications，2022，58（8）：273-282.）

［26]康家兴，牛保宁，郝晋瑶.多参数的城市时空热点查询［J］.计算机工程与应用，2019，55（10）：233-239.（Kang Jiaxing，Niu Baoning，Hao Jinyao.Multi-parameter city hot-spots query［J］.Computer Engineering and Applications，2019，55（10）：233-239.）

［27]Lee J，An M，Kim Y，et al.Optimal allocation for electric vehicle charging stations［J］.Energies，2021，14（18）：5781.

［28]周椿奇，向月，童话，等.轨迹数据驱动的电动汽车充电需求及V2G可调控容量估计［J］.电力系统自动化，2022，46（12）：46-55.（Zhou Chunqi，Xiang Yue，Tong Hua，et al.Track data-driven EV charging demand and V2G adjustable capacity estimation［J］.Power System Automation，2022，46（12）：46-55.）

［29]赵子贤，邵超峰，陈珏.中国省域私人电动汽车全生命周期碳减排效果评估［J］.环境科学研究，2021，34（9）：2076-2085.（Zhao Zixian，Shao Chaofeng，Chen Jue.Evaluation of the effect of carbon emission reduction in the whole life cycle of private electric vehicles in China［J］.Environmental Science Research，2021，34（9）：2076-2085.）

［30]施晓清，李笑诺，杨建新.低碳交通电动汽车碳减排潜力及其影响因素分析［J］.环境科学，2013，34（1）：385-394.（Shi Xiaoqing，Li Xiaonuo，Yang Jianxin.Analysis of carbon emission reduction potential and influencing factors of low-carbon transport electric vehicles［J］.Environmental Science，2013，34（1）：385-394.）

［31]Jain R，Garg S，Gangal S，et al.Taxiscan：a scan statistics approach for detecting taxi demand hotspots［C］//Proc of the 12th International Conference on Contemporary Computing.Piscataway，NJ：IEEE Press，2019：1-6.

［32]張帝，姜久春，张维戈，等.电动出租车充电桩优化配置［J］.电工技术学报，2015，30（18）：181-188.（Zhang Di，Jiang Jiuchun，Zhang Weige，et al.Optimal configuration of electric taxi charging piles［J］.Journal of Electrical Technology，2015，30（18）：181-188.）

收稿日期：2023-02-22；

修回日期：2023-04-03

基金项目：国家自然科学基金资助项目（61761025）

作者简介：周筝（1998-），女，河南平顶山人，硕士研究生，主要研究方向为数据处理、建模分析；龙华（1963-），女（回族）（通信作者），云南大理人，教授，博士，主要研究方向为信息处理、无线通信、信号处理、仿真建模（2923608163@qq.com）；李帅（1996-），男，河南南阳人，硕士研究生，主要研究方向为信息处理、图像处理；梁昌侯（1996-），男，云南保山人，硕士研究生，主要研究方向为数据处理、信息处理.