混合流水车间插单重调度的超启发式遗传算法
2023-10-18刘思宇李铁克王柏琳袁帅鹏张文新
刘思宇 李铁克 王柏琳 袁帅鹏 张文新


摘 要:针对带有紧急订单的混合流水车间插单重调度问题,提出了一种双层编码的超启发式遗传算法。针对混合流水车间具有的订单排序和机器选择的双决策特征,在算法低层设计双层编码方案,在个体中表示订单排序和机器选择两类信息,对应一个唯一调度解,进而提出了12种排序和选择启发式对个体进行迭代优化;在算法高层采用自适应遗传算法,用来确定订单排序启发式和机器选择启发式的操作组合以及各组合执行的次序,并设计了自适应变异算子来优化算法的有效性。大规模数据实验的结果表明,所提算法具有很好的求解质量和求解效率。
关键词:重调度; 混合流水车间; 超启发式; 遗传算法; 紧急插单
中图分类号:TP205 文献标志码:A
文章编号:1001-3695(2023)09-007-0000-00
doi:10.19734/j.issn.1001-3695.2022.12.0831
Hyper-heuristic genetic algorithm for hybrid flow shop with
rush orders insertion rescheduling problem
Liu Siyu1,2, Li Tieke1,2, Wang Bailin1,2, Yuan Shuaipeng1,2, Zhang Wenxin1,2
(1.School of Economics & Management, University of Science & Technology Beijing, Beijing 100083, China; 2.Engineering Research Center of MES Technology for Iron & Steel Production, Ministry of Education, Beijing 100083, China)
Abstract:Aiming at the rescheduling problems of hybrid flow shop with rush order insertion, this paper proposed a hyper-heuristic genetic algorithm based on the two-layer coding. Aiming at the double-decision characteristics of order sort and machine selection in the hybrid flow shop, this algorithm designed a two-layer coding scheme in the low level. Each individual represented both order sort and machine selection information, and corresponded to a unique scheduling solution. Then the low level proposed 12 kinds of sorting and selection heuristics for iterative optimization of individuals. The high level of the algorithm used an adaptive genetic algorithm to determine the operation combination of order sort heuristic and machine selection heuristic and the sort of execution of each combination. And it designed an adaptive mutation operator to optimize the effectiveness of the algorithm. The results of large-scale data experiments show that the proposed algorithm has good solving quality and efficiency.
Key words:insertion rescheduling; hybrid flow shop; hyper-heuristic algorithm; genetic algorithm; rush order insertion
0 引言
隨着制造业水平的不断提高和市场经济的快速发展,企业需要提高服务水平来满足客户的个性化需求。其中,紧急订单是订单型企业面临的常见问题,但它在给企业带来额外利润的同时也对生产的稳定性造成了破坏。在紧急订单到来后,企业需要重新安排生产调度计划,将紧急订单合理安插在原有调度方案中,这对企业生产管理的快速反映能力是个巨大挑战。因此,对紧急订单插单重调度问题的研究具有很高的实际价值理论价值。混合流水车间是一类具有很强工程背景的复杂车间环境,广泛存在于化工、纺织、钢铁、半导体等行业,其调度问题已被证明是强NP(non-deterministic polynomial)难的,因此紧急插单这种动态环境下的混合流水车间重调度问题具有更为复杂的求解难度,是订单型企业亟需解决的重要问题。
在紧急插单重调度问题中,常见的插单方法有退单插单[1]和顺延插单[2]。此外严浩云等人[3]提出了重排插单的方法,并验证了其优越性。近年来,越来越多的学者关注到紧急插单重调度问题。Zakaria等人[4]通过操纵机器上的可用空闲时间和重新排序操作,将重新调度与非重组和重组策略相匹配,并提出了一种改进遗传算法以适应紧急订单的动态插入。Liu等人[5]将匹配策略和实时策略相结合,引入了10种经典优先级规则,并提出了一种新规则。任玺悦等人[6]采用匹配思路设计多紧急订单到达的重调度策略,将重调度计划分为静态调度、基于匹配策略的混合重调度、基于实时策略的剩余原工序重调度三个阶段,采用混合遗传禁忌搜索算法对问题进行求解。由以上文献可知,目前对紧急插单的重调度策略多集中于对原调度的部分改动,虽然保证了计划的相对稳定性。但可能导致无法得到最优结果。
当前对求解插单重调度问题的方法主要集中在元启发式算法上。何小妹等人[7]研究了多目标混合流水车间的紧急插单重调度问题,提出了多目标算法NSGA-Ⅲ(non-dominated sorting genetic algorithm-Ⅲ)。裴小兵等人[8]使用改进的果蝇优化算法寻求带有插单问题的调度最优解,考虑建立三级优先级列表来确定订单的优先级指导初始中心果蝇的产生。紧急订单的插入或取消是引发重调度的常见扰动之一,而目前仅针对插单问题的研究较少,传统方法中,一般将其归于重调度问题中进行解决。Gao等人[9]提出了两阶段人工蜂群算法用来解决柔性作业车间的调度与重调度问题;随后文献[10]进一步改进了上述算法,使其适用于模糊柔性作业车间的调度与重调度问题。裴海燕等人[11]提出了一种改进的遗传算法,对插单扰动下,流水线的生产调度与预防性维护进行联合重调度优化。吉卫喜等人[12]提出异常事件驱动的离散车间重调度决策方法,借助模拟退火算法对最优重调度求解。
综上,运用现有元启发算法求解混合流水车间插单问题主要存在以下两点不足:a)规则策略单一,虽然在部分场景下可以求得较优解,但算法通用性差,调度环境和目标的变化会影响算法的求解能力;b)插单重调度问题解空间呈指数爆炸性增长,常规算法难以实现有效搜索。目前对该问题的求解大多基于元启发式算法的框架,并在其中融入一些局部搜索操作,虽在一定程度上提高了算法的局部搜索效率,但也存在易过早陷入局部最优的问题,算法在平衡全局搜索与局部优化的能力上仍有提升空间。
超启发式算法(hyper-heuristic algorithm,HHA)是一种新型智能优化算法,通过某种高层策略控制多种低层启发式算法(low-level heuristic,LLH)实现对解空间的搜索[13]。目前HHA已经在多领域得到应用,如路径规划问题[14,15]、项目调度问题[16]、组合优化问题[17]等。在生产调度领域上,连戈等人[18]提出一种超启发人工蜂群算法对多场景的鲁棒分布式置换流水车间调度问题进行研究,其中高层控制低层不断生成新的混合启发式算法,实现在不同场景对应解空间中的深入搜索。罗文冲等人[19]针对两阶段分布式装配柔性作业车间调度问题,以最小化最大完工时间为优化目标,提出了一种超启发式交叉熵算法。屈新怀等人[20]以最大完工时间和最小能耗为目标,设计超启发式遗传算法对多目标柔性作业车间绿色调度问题求解,算法解决了启发式算法通用较差的问题。胡蓉等人[21]针对绿色双边装配线平衡问题提出了超启发式三维分布估计算法(hyper-heuristic three-dimensional estimation of distribution algorithm,HH3DEDA),其中三维分布估计算法用于对启发式规则的选择。由文献调研可知,在高层动态控制LLH的过程中,高效的高层控制策略和针对问题特征设计的低层启发式算法,是决定HHA求解性能的关键。综上,将HHA应用于混合流水车间插单重调度问题具有以下优势:a)HHA可以通过高层动态控制和选择低层启发式操作,动态生成与问题适配的多种混合启发式算法,有效解决插单问题中由工序排序和机器选择导致的复杂解空间问题,增加了局部优化能力;b)HHA通用性强,面对不同的生产模式,在不改变算法框架的基础上,调整低层规则即可对求解条件进行有效控制,提高了混合流水车间插单重调度的灵活性。
基于以上分析,本文以最大总完工时间最小化为目标,基于超启发式方法对混合流水车间环境下的紧急订单插单重调度算法展开研究。首先,通过对问题的分析建立了混合流水车间插单重调度的数学模型。进而,设计超启发式遗传算法(hyper-heuristic genetic algorithm,HHGA)对问题进行求解。在超启发式遗传算法中,设计了12种底层启发式操作,并通过高层策略遗传算法对操作组合进行选择。最后,通过数据实验对算法性能进行验证。
1 问题描述及分析
混合流水车间插单重调度问题描述如下:企业在生产的初始时刻,已定好了现有的n个订单在流水线S个阶段的生产计划,各阶段至少有一台机器且至少有一个阶段存在并行机,每道工序可在相应阶段任意一台机器上加工,各并行机处理时间相互独立。每个订单只包含一种工件。在加工开始前,紧急订单k到达。现要将该紧急订单插入到该生产批次中,寻求最优的订单加工顺序和订单在各阶段的机器选择,使得所有订单的最大完工时间最小。为便于描述,表1定义了问题的参数和变量。
目标函数式(1)为最小化最大完工时间;约束式(2)定义了订单在最终工序S的完工时间,即订单总完工时间由各订单最后工序完工时间决定;约束式(3)要求每一订单在前一工序完成后方可进入下一工序;约束式(4)表示订单加工过程连续且不可中断;约束式(5)表示同一机器不能同时加工多个订单,即被选用的机器同一阶段不能有交叠使用时间;约束式(6)确保每一订单的任一工序只能在一台机器上处理;约束式(7)表示被安排在同一阶段同一机器的工序,排序靠前的先加工;式(8)和(9)是变量取值约束。
2 超启发式算法设计
2.1 算法思路与求解框架
在HHGA中,高层是策略域,由12种启发式操作经过不同排列组合而成,种群中的每个个体代表一种更新策略;低层是问题域,由工序码和机器码串联组成,种群中的每个个体代表原问题的一个解。在求解过程中,高层策略域首先利用遗传算法对种群个体进行优化,即改变低层多个启发式操作的组合顺序,从而得到新的高层策略域个体。而后更新后的高层策略域个体分别对应于每一个低层问题域个体,控制低层个体执行并行的变邻域搜索,每一个低层个体均执行了工序码和机器码的更新操作,得到新的低层个体。若更新操作后的解优于旧解,则用新解代替旧解。所有个体中适应值的最优解即为原问题的目标函数值。HHGA的两层结构如圖1所示。
2.2 高层策略域的遗传算法
遗传算法是一种基于自然界生物群体适者生存、优胜劣汰的元启发算法,具有待定参数少、收敛速度快、不易陷入局部最优等特点。在本文提出的HHGA中,高层策略域设计了一种自适应遗传算法来确定低层启发式的执行顺序。
2.2.1 编码方案
对于高层策略域,高层的每一个个体均由低层启发式操作的不同排列组成,也即高层的编码,启发式操作可重复出现。高层每一个染色体的长度等于低层启发式操作的个数的总和。在本文算法中,低层由12个启发式构成,包括6个订单排序启发式和6个机器选择启发式,分别命名为LLH1~LLH6和LLH7~LLH12,具体将在2.3节中详细阐述,对应到高层算法编码中,则采用序号1~12来表示。
2.2.2 解码方案
在对高层个体解码时,由于低层启发式操作分为对工序排序和对机器选择两种,因此需依次执行染色体对应的基因位组合的操作。解码方案的伪代码如下:
算法1 高层个体解码方法
输入:高层染色体;原始解。
输出:新解。
input:Chrom;Objv1; //输入高层染色体;原始解
Chrom1=Chrom(1:6);
Chrom2=Chrom(7:12); //将染色体分成工序码和机器码;
for i=1:6
switch Chrom1(i)
case x //x=(1,2,…,6)
do LLH(x); //执行工序码对应位置的启发式操作
chrom1=Chrom1′;
switch Chrom2(i)
case y //y=(1,2,…,6)
do LLH(y); //执行工序码对应位置的启发式操作
chrom2=Chrom2′;
chrom′=[Chrom1 Chrom2]; //更新后的染色體
Objv2=f(Chrom′); //新的适应值
if Objv1>Objv2 //如果新解优于旧解
BestObjv=Objv2; //新解替换旧解
Objv1=Objv2;
break;
else
continue; //保留旧解继续执行循环
end if
end for
图2为一个高层染色体示意图,该染色体为1-2-5-4-3-6-7-9-12-10-8-11,表示对对应的底层个体首先执行订单排序启发式LLH1+机器选择启发式LLH7,进而依次执行LLH2+LLH9、LLH5+LLH12、LLH4+LLH10、LLH3+LLH8、LLH6+LLH11的操作组合。为避免操作次数太多导致染色体过度重组,每执行一次操作组合则计算当前方案的最大完工时间,若有所改进则停止执行后续组合。启发式操作执行更新完成后的值即为染色体的适应值。
2.2.3 自适应的遗传进化操作
遗传进化的主要操作为选择、交叉、变异。
选择操作采用轮盘赌的方法按概率选择适应值较强的染色体参与遗传,选择概率由适应函数决定。由于本文的目标是最大完工时间最小,而在轮盘赌中,适应值越大的个体被选择的几率越大,因此适应函数采用目标函数的倒数,表达式如下:
p(x)=1f(x)(10)
交叉操作采用两点交叉,即在互相配对的两个染色体中随机设置两个交叉点,交换两个在所设定的两个交叉点间的部分染色体,形成新的子代种群。交叉操作是否执行由交叉概率PC控制。交叉操作表达式如下,r为0~1的随机数。
Xnewi=Xoldi r>PC
Xnewiotherwise i=1,2,…,n(11)
变异操作采用单点变异,即在染色体上随机选择一个变异位置,将该位置随机替换成一个合法的染色体基因。变异操作采用参考文献[13],由自适应变异算子PM控制。自适应算子的表达式如下:
PM=0.1×α×genmax gen(12)
其中:gen表示当前迭代次数;maxgen表示总迭代次数;α是变化速率,它控制着变异概率增大的速率。随着迭代次数的增加,变异概率也增大,这有助于到迭代后期帮算法跳出局部最优。
2.3 低层问题域的启发式操作
2.3.1 编码方案
对于低层问题域,采用基于工序码与机器码的双层编码方式。其原因是双层编码可以同时描述订单的加工顺序和加工机器的选择两种信息,共同完整表达问题的解。第一层为工序码,不同的数字代表相应的订单号,号码出现的次数表示该订单的工序数;第二层为机器码,机器码的索引号代表对应的订单工序在可选机器集里所选择的机器。由于低层个体由工序码和机器码共同组成,所以低层问题域中每个个体都代表着原问题的一个解,即原问题的一种调度方案。该调度方案的含义是:各订单各工序所选择的加工机器。
图3给出了一个编码示例,其编码为[1,1,2,1,2,2,1,3,1,2,2,1]。可以看出,其工序码为[1,1,2,1,2,2],表示工序按照{O1,1, O1,2, O2,1, O1,3, O2,1, O2,3}的顺序加工;机器码为[1,3,1,2,2,1],表示所选用的机器编号为{1,5,6,2,4,6}。
2.3.2 低层问题域的启发式操作
低层启发式操作决定了对问题解空间的搜索程度和解的质量。本文针对双层编码的特点,将低层启发式操作设计为针对工序码和机器码的两部分。从订单和机器这两个局部变化的角度出发构建策略池如下:
1)基于工序的操作
工序码由LLH1~LLH6构成,其中LLH1~LLH2为针对工序排序设计的策略,LLH3~LLH6为四种经典的邻域变换操作。
a)LH1(随机插入)。从工序排列中随机选择一个工序码,将之插入到工序排列中的随机位置。
b)LLH2(随机多点插入)。从工序排列中随机选择三个工序码,将它们随机插回原有的工序排列中。
c)LLH3(工序码随机交换)。随机从工序码中选取两个进行交换。
d)LLH4(工序码相邻交叉)。随机从工序排列中选择相邻的两位,将它们交换。
e)LLH5(随机反转)。从工序码序列中随机选取长度为a的子序列,将其翻转后,放入回原有序列。
f)LLH6(随机前移)。从工序码序列中随机选取长度为a的子序列,将其移动到序列的最前端。
2)基于机器选择的操作
机器码由LLH7~LLH9构成,其中LLH7~LLH9为针对机器选择设计的策略,同时引入LLH10~LLH12三种经典的机器选取规则。
a)LLH7(單个机器码变异)。从机器码中随机选择一个,将其随机变成可选机器码中的某个。
b)LLH8(多个机器码变异)。从机器码中随机选择多个,将其随机变成可选机器码中的某个。
c)LLH9(机器码子序列变异)。随机选取机器码子序列,将子序列上每一个机器码随机变成该位置可选机器码中的某个。
d)LLH10(机器最短加工时间规则)。将全部机器码替换成按照对应工序可选机器集中加工时长最小的机器的索引号。
e)LLH11(工序最早开始加工规则)。根据工序排序,将机器码按照能满足当前工序最早开始的条件重排。
f)LLH12(工序最早结束规则)。根据工序排序,将机器码按照能满足当前工序最早结束的条件重排。
2.4 HHGA算法步骤
HHGA算法步骤描述如下:
a)初始化高层策略域和低层问题域种群。随机生成长度为低层启发式操作总个数的高层个体,和长度为双倍工序总数的低层问题域个体。高层和低层对应的种群大小相同且染色体一一对应。
b)对每一个高层个体依次执行底层操作,根据目标函数计算得到解的适应值。高层和低层的适应值大小相同。
c)用轮盘赌选出策略域种群的精英解,进行交叉变异。
d)用更新后的策略域个体依次执行对应的启发式操作组合,更新问题的解,若新解的适应值优于旧解,则不再执行后续的低层启发式操作组合,否则继续执行。若全部新解均不优于旧解,则保留旧解。
e)判断是否全部低层问题域种群均已被更新,若已完成,则对两个域中的种群进行保优,将精英解放入对应种群。若没有,则转入步骤d)。
f)判断迭代次数是否达到最大值,若没有,转入步骤c),否则终止循环。
2.5 算法示例说明
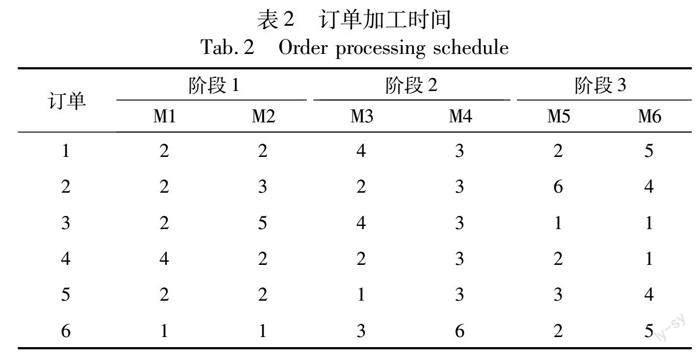
为了更直观地阐述本文HHGA算法运算过程,给出了一个小规模(6×3×6)的混合流水车间插单重调度问题作为算法示例,具体加工时间如表2所示,参数设置同3.1节,最大迭代次数为50。其中,订单1~5为已排定的订单,订单6为紧急订单,需将其插入到现有调度中。
首先,随机初始化高层和低层种群,得到的高层个体1为{1,4,3,2,5,6,11,9,10,12,7,8},低层个体1为{4,2,1,6,6,1,2,3,5,4,4,6,2,3,5,3,5,1,1,1,1,1,1,2,2,1,2,2,1,2,2,1,2,2,1,1}。对低层个体1进行解码,得到的目标值Cmax为24。
进而,用自适应遗传算法对高层个体进行第一次进化迭代,更新后的高层个体1为{2,6,5,1,4,3,9,8,12,10,11,7},用其对低层个体1更新,在执行到组合LLH4+LLH11时,得到该个体的最优解17。更新后的低层个体1为{2,3,6,4,4,5,3,2,1,6,6,1,2,4,3,5,5,1,1,2,1,1,1,2,1,2,1,2,1,2,1,1,1,1,1,1}。依次更新完种群全部个体后,进行保优操作,得到种群全部个体的最优解为14。
循环迭代上述过程,在达到最大迭代次数50时算法终止。实验结果表明,HHGA算法在进化到第6代时即收敛到算例的最优解12,得到的最优重调度方案如图4所示。在该方案中,订单6被插在订单2后进行加工。
为进一步探究本文算法的有效性,将本算例应用于3.3节的三种对比算法:单层编码超启发式遗传算法(single-level hyper-heuristic genetic algorithm,S-HHGA)、超启发差分进化算法(hyper-heuristic differential evolution algorithm,HHDE)[22]、双层编码遗传算法(double genetic coding genetic algorithm,DGCGA)[23](有关对比算法的说明详见3.3节)。考虑到本文HHGA算法在迭代到第6代时即取得最优解12,实验中将对比算法的最大迭代次数设为6,以便观察在相同迭代次数下各算法的求解效果,实验结果如表3所示。
由表3可知,本文算法HHGA相对于其他三种算法有着明显优势。首先,HHGA可以生成高质量的初始解,即使对于解空间有限的小规模问题,HHGA得到的初始解也能明显优于对比算法;其次,HHGA具有较快的收敛速度,在进化到第6代时,仅HHGA收敛到了最优解12。因此,HHGA在初始解质量和收敛速度方面均具有很好的性能。
此外,由实验结果可以观察得出,采用超启发式方法的HHGA、S-HHGA和HHDE的求解效果均明显优于元启发式DCAGA,这说明了超启发式算法对解决混合流水车间插单重调度问题的适用性。
3 实验设计与分析
3.1 算法参数设计
算法的参数设置对算法性能有重要影响。HHGA中的算法关键影响参数包括:种群规模P,交叉率PC,变化速率α。其中,种群规模P和交叉率PC来源于高层策略遗传算法,根据文献[24]可知,常用的参数范围为P=20~200,PC=0.5~1。为进一步确定针对本文算法的参数有效取值范围,在上述参数范围内对算例进行了多次预测式实验,根据测试效果,最终将种群规模P的取值范围限定在10~40,交叉率PC则为0.6~0.9。 变化速率α来源于文献[13],本文直接引用其参数设置值。为了探讨参数设置对算法性能的影响,本文采用田口实验设计法[25]进行实验。针对HHGA每个参数设置4个水平值,如表4所示。选用随机生成的中等规模的数据(20×5×11),对HHGA每种参数组合独立运行10次,取它们的平均值作为平均响应值ARV,结果如表5所示。
根据表5进一步统计了各参数响应值对算法性能的影响,结果如表6所示。根据表6对三个主要参数的变化对算法性能的影响分析如下:种群规模P过小,算法优化性能不明显,易陷入局部最优;规模過大易导致求解时间过长。交叉算子PC的大小影响个体间的交换频率,个体间交流次数增多,有利于搜索到全局最优解。自适应变异算子α的变化速率越大,迭代后期变异率越大,会导致高层策略遗传算法发散,破坏个体稳定性,因此选用较小值。
根据表6可以看出,当P=30,PC=0.8,α =10时算法具有最优性能,算法的实验参数将依此设置。
3.2 实验环境与数据
为测试HHGA的性能,本文选取了文献[22]的HHDE和文献[23]的DGCGA作为对比。为验证双层编码方式的有效性,以本文HHGA为框架设计了S-HHGA作为对比算法。将这三种对比算法应用于本文问题。在参数设置上,前两种对比算法均采用原文献推荐的参数值,S-HHGA的参数与本文算法保持一致。四种算法的最大迭代次数统一设为500。此外 ,由于本文问题和文献算法研究的问题不完全一致,所以对S-HHGA和HHDE均采用选择使当前工序最早开始加工的解码方式。
为检验算法在不同问题规模下的求解性能,将算例的问题规模设置如下:订单数n={10,20,30,50,100};工序数S={5,8,10};单个工序可选机器数m={1,2,3,4}。总机器数为各工序可选机器数的总和。根据问题规模分成15组实验,每组随机生成10个算例。四个算法均采用MATLAB R2015b编程,运行环境为Intel CoreTM i5-7200U CPU @ 2.50 GHz 2.70 GHz和RAM 8.0 GB。
3.3 实验结果与比较
算法性能从算法有效性的角度,以最大完工时间最小化为评价指标。采用相对偏差率(percentage relative difference,PRD)[26]来衡量算法性能计算公式如式(13),其中α为当前算法A所求得的目标函数Cmax值,CBest为所有算法求得的最好Cmax值。
PRD=Cmax(A)-CbestCbest×100%(13)
针对15组问题规模用上述算法分别求解,计算每种算法的PRD均值和标准差,并采用方差分析(analysis of variance,ANOVA)对每种算法PRD均值的差异性进行显著性检验(γ=0.05)。实验结果如表7所示。
由表7统计结果可以看出:
a)测试的所有规模问题经过ANOVA分析得到的P-value值均接近于0,远小于α,这说明四种算法在求解质量上存在显著差异。从表4的avg和std指标来看,除100×5×11的问题规模外,HHGA在其他规模问题上均取得了最小平均值。以上结果表明,HHGA的双层结构有效避免了单一搜索策略或简单邻域操作导致的搜索深度有限问题,在求解性能的稳定性上优于其他三种算法。
b)与S-HHGA相比,本文算法的PRD均值降低了77.8%,这说明双层编码策略能容纳更多的信息,使遗传算法方便用于复杂问题的求解,同时避免了单一解码策略易陷入局部最优的不足,合理规定了问题的搜索空间,在求解质量上要高于单层编码。
c)与HHDE相比,HHGA的PRD均值和标准差平均降低80%、27.5%,这说明本文设计的高层策略域在寻求优质解上是有效的,相比于差分算法,在动态控制和选择低层启发式操作时,能生成更多有效的混合式启发式算法对问题求解,增加了算法的求解深度。
d)与DGCGA相比,HHGA的PRD均值降低了90.7%,这验证了本文算法的有效性,相比于传统遗传算法容易陷入局部最优的缺点,HHGA通过其两层结构,由高层对低层启发式操作的排序进行优化,使得低层可执行更紧凑的变邻域搜索,从而增强了算法跳出局部最优的能力,更容易发现复杂解空间的较优解。
为进一步检验HHGA的收敛效率和求解质量,随机选择一个规模为10×5×11的算例给出四种算法迭代500次的收敛曲线对比,如图5所示。从图5可看出,在收敛效率上,HHGA在第170次迭代中取得最优目标值103,其收敛速度最快,且求解效果远超其他三种算法。在寻优能力上,单层HHGA的最优值123小于HHDE的最优值130,且两种算法求解结果均大于HHGA。这一方面说明双层编码策略的有效性,另一方面说明改进后的HHGA具有良好的求解性能。
3.4 订单规模的敏感性分析
订单规模是混合流水车间插单重调度问题的重要参数,其变化往往会影响到问题求解的难度。为确定订单规模变化对问题求解难度的影响,本文选取工序数为中等规模8且固定机器数量为18的车间环境,设计订单规模分别为10、20、30、50和100的算例组,针对每组由随机生成的10个算例组成,并采用3.2节的四种算法求解,实验结果取最大完工时间的平均值。通过该实验,一方面观察订单规模对算法性能的总体影响趋势,以此确定订单规模对问题求解难度影响;另一方面则进一步对比四项基本原则种算法的求解效果,检验本文HHGA的有效性。
实验结果如图6所示,可以看出,首先,随着订单规模的增加,四种算法的Cmax均呈现出明显上升趋势,其中HHGA的增长趋势较缓,这说明订单规模会明显延长车间的制造周期,但如果采用合适的算法则可以减缓这一因素变动的影响。其次,DGCGA的增长速度始终最快,这说明超启发式算法在稳定性上较优于传统算法,其双层结构使低层的变邻域搜索更加细致,解的质量更好。再次,在订单数小于50时,S-HHGA的斜率小于HHGA,加工时间增长速度比HHGA慢,当订单大于50时,HHGA的变化趋势要比S-HHGA平稳,这说明在HHGA在大规模问题上,更具优势,这是因为随着订单数量的增多,有效的机器选择规则能使问题在求解中跳出局部最优,得到更满意的解。
3.5 实例仿真分析
由于目前对该类问题研究较少,尚不存在benchmark数据集进行实例分析,本文选取文献[27]提供的钢铁生产实际数据。实例对应钢铁生产中某炼钢—精炼—连铸—轧制过程,有3台炼钢炉、3台精炼炉、2台铸机和2台轧机,各阶段存在不相关并行机,且机器加工能力不同,具体加工时间如表8所示。假设在开始加工前,已安排好前11个订单的加工顺序,现插入订单12重新排序。4种算法独立运行10次仿真结果如表9所示。
表9可知,HHGA的结果要优于其他三种算法的结果,且相对鲁棒。就整体性能而言,只有HHGA寻得了最优解304,算法的性能也优于其他三种。因此,HHGA在混合流水车间插单重调度问题上的寻优性能和稳定性上都优于本文设定的对比算法。
4 结束语
本文针对混合流水车间的紧急订单插单重调度问题,以最小化最大完工时间为优化目标,提出了一种双层结构的超启发式遗传算法(HHGA)。该算法采用GA作为高层策略,动态控制和选择低层的12种启发式操作,生成有效混合启发式算法对问题求解。本文的HHGA有如下特点:a)低层编码采用工序码加机器码的双层形式,提高了低层染色体的信息容量,避免了单一解码策略易陷入局部最优的不足;b)算法高层动态控制12种启发式操作来持续生成新的混合启发式算法,可实现对问题解的深度搜索;c)算法高层采用自变异交叉算子的遗传操作,避免算法过早陷入局部最优;d)在低层启发式操作的设定上,除经典的邻域变化外,加入机器选取规则,合理限定了问题的搜索空间。最后,本文采用田口实验法对算法中的主要参数进行确定,并通过大规模实验和算法比较验证了所提HHGA的有效性。后续工作将对HHGA的高层策略进一步优化,同时考虑机器故障等其他扰动情况。
参考文献:
[1]胡东波,王国庆,左小德.实时动态排产系统研究[J].中国机械工程,2004,15(8):698-703,738.(Hu Dongbo,Wang Guoqing,Zuo Xiaode.Study on real-time dynamic production schedule system[J].China Mechanical Engineering,2004,15(8):698-703,738.)
[2]唐国兰,唐成华,吴云忠.车间生产计划动态调整应用研究[J].机电工程技术,2004,33(8):92-94.(Tang Guolan,Tang Chenghua,Wu Yunzhong.Study on the application of dynamic adjustment of workshop production plan[J].Mechanical & Electrical Engineering Technology,2004,33(8):92-94.)
[3]嚴浩云,李宏余.基于面向负荷的生产控制的紧急订单插单问题[J].计算机集成制造系统,2009,15(9):1809-1815.(Yan Haoyun,Li Hongyu.Rush order inserting problem based on load-oriented manufacturing control technique[J].Computer Integrated Manufacturing Systems,2009,15(9):1809-1815.)
[4]Zakaria Z,Petrovic S.Genetic algorithms for match-up rescheduling of the flexible manufacturing systems[J].Computers & Industrial Engineering,2012,62(2):670-686.
[5]Liu Weibo,Yan Jin,Price M.New scheduling algorithms and digital tool for dynamic permutation flow shop with newly arrived order[J].International Journal of Production Research,2017,55(11):3234-3248.
[6]任玺悦,王修贤,耿娜,等.考虑多急件到达的作业车间重调度研究[J].工业工程与管理,2022,27(3):74-83.(Ren Xiyue,Wang Xiuxian,Geng Na,et al.Research on job shop rescheduling considering rush orders[J].Industrial Engineering and Management,2022,27(3):74-83.)
[7]何小妹,董绍华.多目标多约束混合流水车间插单重调度问题研究[J].工程科学学报,2019,41(11):1450-1457.(He Xiaomei,Dong Shaohua.Research on rush order insertion rescheduling problem under hybrid flow shop with multi-objective and multi-constraint[J].Chinese Journal of Engineering,2019,41(11):1450-1457.)
[8]裴小兵,楊景霞.一种解决带有紧急插单问题的果蝇优化算法[J].系统工程,2020,38(6):139-146.(Pei Xiaobing,Yang Jingxia.An improved fruit fly optimization algorithm for problem with urgent orders insertion[J].Systems Engineering,2020,38(6):139-146.)
[9]Gao Kaizhou,Suganthan P N,Tasgetiren M F,et al.Effective ensembles of heuristics for scheduling flexible job shop problem with new job insertion[J].Computers & Industrial Engineering,2015,90(12):107-117.
[10]Gao Kaizhou,Suganthan P N,Chua T J,et al.A two-stage artificial bee colony algorithm scheduling flexible job-shop scheduling problem with new job insertion[J].Expert Systems with Applications,2015,42(21):7652-7663.
[11]裴海燕,蒋祖华,胡家文,等.插单扰动下流水线生产与维护的重调度优化[J].工业工程管理,2017,22(1):50-57.(Pei Haiyan,Jiang Zuhua,Hu Jiawen,et al.Integrating rescheduling with preventive maintenance in the flow-shop problem under rush orders[J].Industrial Engineering and Management,2017,22(1):50-57.)
[12]吉卫喜,蔡酉勇,张朝阳,等.异常事件驱动的离散制造车间重调度决策[J].系统仿真学报,2018,30(11):4043-4052.(Ji Weixi,Cai Youyong,Zhang Chaoyang,et al.Abnormal event driven rescheduling decision making in discrete manufacturing workshop[J].Journal of System Simulation,2018,30(11):4043-4052.)
[13]李尚函,胡蓉,钱斌,等.超启发式遗传算法求解模糊柔性作业车间调度[J].控制理论与应用,2020,37(2):316-330.(Li Shanghan,Hu Rong,Qian Bin,et al.Hyper-heuristic genetic algorithm for solving fuzzy flexible job shop scheduling problem[J].Control Theory & Applications,2020,37(2):316-330.)
[14]张景玲,冯勤炳,赵燕伟,等.基于强化学习的超启发算法求解有容量车辆路径问题[J].计算机集成制造系统,2020,26(4):1118-1129.(Zhang Jingling,Feng Qinbing,Zhao Yanwei,et al.Hyper-heuristic for CVRP with reinforcement learning[J].Computer Integrated Manufacturing Systems,2020,26(4):1118-1129.)
[15]赵燕伟,冷龙龙,王舜,等.进化式超启发算法求解多车型低碳选址—路径问题[J].控制与决策,2020,35(2):257-271.(Zhao Yanwei,Leng Longlong,Wang Shun,et al.Evolutionary hyper-heuristics for low-carbon location-routing problem with heterogeneous fleet[J].Control and Decision,2020,35(2):257-271.)
[16]Song Hongbo,Lin Jian.A genetic programming hyper-heuristic for the distributed assembly permutation flow-shop scheduling problem with sequence dependent setup times[J].Swarm and Evolutionary Computation,2021,60:100807.
[17]Jian Lin.Backtracking search based hyper-heuristic for the flexible job-shop scheduling problem with fuzzy processing time[J].Engineering Applications of Artificial Intelligence,2019,77(1):186-196.
[18]连戈,朱荣,钱斌,等.超启发式人工蜂群算法求解多场景鲁棒分布式置换流水车间调度问题[J].控制理论与应用,2023,40(4):713-723.(Lian Ge,Zhu Rong,Qian Bin,et al.Hyper-heuristic artificial bee colony algorithm for the multi-scenario-based robust distributed permutation flow-shop scheduling problem[J].Control Theory & Applications,2023,40(4):713-723.)
[19]罗文冲,钱斌,胡蓉,等.超启发式交叉熵算法求解分布式装配柔性作业车间调度问题[J].控制理论与应用,2021,38(10):1551-1568.(Luo Wenchong,Qian Bin,Hu Rong,et al.Hyper-heuristic cross entropy algorithm for distributed assembly flexible job-shop scheduling problem[J].Control Theory & Applications,2021,38(10):1551-1568.)
[20]屈新怀,纪飞,孟冠军,等.超启发式遗传算法柔性作业车间绿色调度问题研究[J].机电工程,2022,39(2):255-261.(Qu Xinhuai,Ji Fei,Meng Guanjun,et al.Green scheduling of flexible job-shop based on hyper heuristic genetic algorithm[J].Journal of Mechanical & Electrical Engineering,2022,39(2):255-261.)
[21]胡蓉,丁帅,钱斌,等.超启发式三维EDA求解绿色双边装配线平衡问题[J].系统仿真学报,2023,35(3):454-469.(Hu Rong,Ding Shuai,Qian Bin,et al.Hyper-heuristic three dimensional estimation of distribution algorithm for solving green two-sided assembly line balancing problem[J].Journal of System Simulation,2023,35(3):454-469.)
[22]沈鹏,王艳,纪志成,等.超启发式DE算法求解零等待发酵工艺调度[J].系统仿真学报,2020,32(11):2235-2243.(Shen Peng,Wang Yan,Ji Zhicheng,et al.Hyper-heuristic DE algorithm for solving zero-wait fermentation process scheduling[J].Journal of System Simulation,2020,32(11):2235-2243.)
[23]李平,唐秋华,夏绪辉,等.基于双层遗传编码的柔性作业车间自适应重调度研究[J].中国机械工程,2013,24(16):2195-2201.(Li Ping,Tang Qiuhua,Xia Xuhui,et al.Self-adaptively rescheduling flexible job shop with double genetic coding[J].China Mechanical Engineering,2013,24(16):2195-2201.)
[24]席裕庚,柴天佑,恽为民.遗传算法综述[J].控制理论与应用,1996,13(6):697-708.(Xi Yugeng,Chai Tianyou,Yun Weimin.Survey on genetic algorithm[J].Control Theory & Applications,1996,13(6):697-708.)
[25]李铁克,栾治伟,王柏琳,等.求解板坯倒垛和落位问题的分布估计算法[J].系统工程理论与实践,2017,37(11):2955-2964.(Li Tike,Luan Zhiwei,Wang Bailin,et al.Estimation of distribution algorithm for solving the slab stack shuffling and relocation problem[J].Systems Engineering Theory & Practice,2017,37(11):2955-2964.)
[26]Wang Bailin,Huang Kai,Li Tieke.Permutation flow shop scheduling with time lag constraints and makespan criterion[J].Computers & Industrial Engineering,2018,120(6):1-14.
[27]崔建双,李铁克,张文新.混合流水车间调度模型及其遗传算法[J].北京科技大学学报,2005,27(5):623-626.(Cui Jianshuang,Li Tieke,Zhang Wenxin.Hybrid flowshop scheduling model and its genetic algorithm[J].Journal of University of Science and Technology Beijing,2005,27(5):623-626.)
收稿日期:2022-12-26;
修回日期:2023-03-20
基金项目:国家自然科学基金资助项目(71701016,71231001);教育部人文社会科学研究青年基金资助项目(17YJC630143);北京市自然科学基金资助项目(9174038);中央高校基本科研业务费资助项目(FRF-BR-20-04B)
作者简介:刘思宇(1998-),女,吉林公主嶺人,硕士研究生,主要研究方向为生产计划与调度;李铁克(1958-),男,吉林长春人,教授,博导,博士,主要研究方向为先进制造管理、生产计划与调度;王柏琳(1983-),女(通信作者),河北石家庄人,副教授,硕导,博士,主要研究方向为生产调度优化(wangbl@ustb.edu.cn);袁帅鹏(1993-),男,河南郑州人,讲师,博士,主要研究方向为先进制造管理、智能优化算法;张文新(1966-),男,河北保定人,副教授,硕士,主要研究方向为生产计划与调度、先进制造管理.
