基于变量聚类分析的烧结矿还原性能预测模型
2023-10-18廖东郑兆颖邢相栋卞卫新张宝婷
廖东,郑兆颖,邢相栋,卞卫新,张宝婷
(1.广西北港新材料有限公司,广西 北海 536000;2.西安建筑科技大学冶金工程学院,陕西 西安 710055;3.陕钢集团汉中钢铁有限责任公司,陕西 汉中 712400)
高炉炼铁作为现代炼铁的主要方法,产量占世界生铁总产量的95%以上。烧结矿是高炉炼铁主要原料之一,质量对后续的冶炼工作至关重要,其还原性能对高炉操作和消耗均有重要影响[1-2]。影响烧结矿还原性的因素包括粒度、气孔率、矿物组成及结构、脉石成分等。传统烧结矿RI的检测方法滞后,检验过程繁琐复杂,耗时较长。因此,快速预测烧结矿RI,实时提出改善RI的调控因素,对于获取高品质烧结矿具有重要的指导作用,已成为目前烧结矿生产的重点研究方向。
聚类分析用来研究影响因素之间不同程度的相似性,达到“物以类聚”的效果。变量聚类作为聚类分析中的一种方法,过程简单,耗时较短,近年来越来越多地应用于工业生产数据分析和性能指标预测等领域[3]。 陈少飞等[1]利用聚类分析处理高炉炼铁数据离群问题,将 “无效离群点”剔除的同时,最大程度保留了 “有效离群点”,保证了高炉炼铁数据的稳定性以及处理的准确性,全面筛选得到能够反映炉况波动的强相关变量,完成了对高炉炉况变化的详细划分。鲁杰等[4]关于高炉操作炉型的研究中,对冷却壁温度进行聚类分析,解决了指标重复性大的问题,准确合理地表征了高炉操作炉型的状况及变化原因,为高炉炼铁大数据分析中的聚类算法选择提供了有利参考。Johanna等[5]根据 k-means聚类分析了粉尘吸入后的数据,聚类区分了三种相似程度小的操作条件作为探索性分析,评估了工业回转窑加注粉尘前后的运行情况,为回转窑-电炉工艺注入粉尘提供了理论指导。然而,目前对铁矿粉烧结领域的有关预测中,更多是集中在燃耗、成品率、转鼓指数等技术指标方面[6-9],针对冶金还原性能的预测较少,尚未实现工业化应用。
因此,基于某钢厂400 m2烧结机产品检测数据,调研分析了60组烧结矿RI及化学成分,采用变量聚类得到影响烧结矿RI的新因子,展开最佳子集回归,得到最佳子集。基于观测值的方差膨胀因子(variance inflation factor,VIF)、Durbin-Watson统计量和Grubbs检验统计量,对回归方程进行异常值检验,建立预测回归模型,并利用测试集进行回归模型误差验证,为改善烧结矿RI提供参考。
1 烧结工艺
现代烧结主要用于生产高炉所需的具有一定转鼓强度和冶金性能的烧结矿。烧结过程示意图如图1所示。

图1 烧结过程示意图Fig.1 Sintering Process Diagram
烧结原料包括铁矿石、石灰石、白云石、生石灰、焦粉和其他少量添加物,各组分经过输送系统到混合机充分混合,以获得化学成分均匀稳定的混合料。随后进入烧结系统,包括布料器、点火器、烧结机、风箱、排气除尘设备等,进行烧结焙烧得到烧结矿。最后烧结矿经破碎、筛分、冷却得到烧结产品。
烧结生产是通过调整烧结过程中的原料参数配比、操作参数和设备参数来优化烧结矿性能。其中,混合料的化学成分很大程度地影响了烧结矿还原性。因此,建立合适的烧结矿还原性预测模型对于提高烧结矿质量具有重要意义。
2 数据处理
2.1 变量聚类
调研60组监测烧结矿RI和化学成分的训练集,选取 TFe、CaO、SiO2、Al2O3、MgO、S、TiO2、R、FeO、MgO/Al2O3、CaO/TFe和SiO2/Al2O3共12种因子作为变量,进行变量聚类分析。利用变量聚类对具有相同特征的聚类变量进行分组,通过指标降维选择有代表性的指标并生成一些新变量[2]。结合凝聚层次法,将相似的变量组合在一起,减少要分析的变量数。
2.2 最佳子集回归
最佳子集回归是根据所有预测变量集生成最高决定系数R2的子集模型,能够有效识别最优模型,估计回归系数,使预测未知响应得到的方差比所有预测变量的完整模型的方差更小[10-11]。将变量聚类的结果作为自变量,RI作为因变量,建立烧结矿RI的预测模型。
3 分析与讨论
3.1 变量聚类
为了全面反映变量对RI的影响,利用降维的思想,将 TFe、CaO、SiO2、Al2O3、MgO、S、TiO2、R、FeO、MgO/Al2O3、CaO/TFe 和 SiO2/Al2O3共 12 种因 子通过联结法定义聚类之间的距离,利用最长距离法,确保聚类中的所有因子都在最大距离范围内,并趋向于生成具有类似直径的聚类。以欧式距离作为相似性统计量,采用最长距离法进行变量聚类,共进行了10步,最终合并了2类。用两点间的距离定义相似性水平,距离水平越小,表明彼此位置越近,样本间差异越小,得到的变量聚类分析结果如表1所示,聚类分析树状图如图2所示。

表1 变量聚类分析结果Table 1 Analysis Results of Variable Clustering
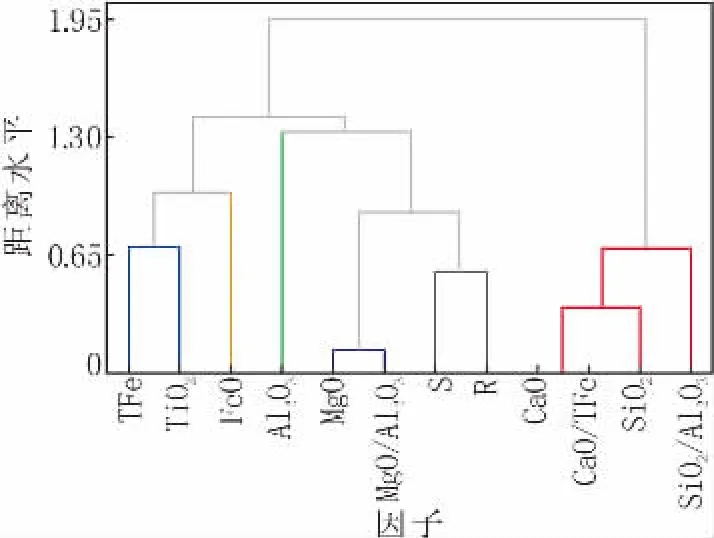
图2 聚类分析树状图Fig.2 Tree Diagram for Clustering Analysis
由表1可以看出,当点群数为2时,相似性水平最低,距离水平最高,分别为29.744 6和1.405 11,此时新聚类号中观测值的个数为8个因子。由图2可以看出, 变量聚类得到 TiO2、FeO、Al2O3、MgO、S、R、CaO/TFe和SiO2共8个因子,即烧结矿 RI的新因子。
3.2 最佳子集回归模型
为了生成最高R2值的子集模型,采用最佳子集回归,得到回归模型。根据3个标准进行模型筛选:①R2达到最大。②预测平方和PRESS达到最小。③Mallows Cp值接近且小于预测变量个数。④距离偏差S达到最小。计算模型分别如式(1)~(4)所示。
式中,SS误差为误差距离平方和;S S合计为总误差平方和;yi为第i个观测响应值;为第i个拟合响应值;为平均响应值;ei为第i个残差值;hi为 X(XTX)-1XT(X 为设计矩阵,XT为设计矩阵的转置)中第i个对角线元素;SSE为残差平方和;MSE为平均误差平方;n为观测值个数;p为模型中的项数;为指代在含K个自变量的线性回归模型中第i个y样本数据的拟合值。
以烧结矿RI为因变量,SiO2、Al2O3、MgO、S、TiO2、R、FeO和CaO/TFe为自变量,建立烧结矿RI的最佳子集回归模型,如表2所示。
由表2可以看出,七变量模型{SiO2、MgO、S、TiO2、R、FeO、CaO/TFe}方差较小,表明数据值与拟合值的距离小,模型描述响应的程度高。七变量模型{SiO2、Al2O3、MgO、S、R、FeO、CaO/TFe}Mallows Cp值为8,正好等于模型项数加预测变量个数,模型相对精确。六变量模型{SiO2、MgO、S、R、FeO、CaO/TFe}R2较高,表明模型拟合数据的优度高,预测能力出色。六变量模型{SiO2、MgO、TiO2、R、FeO、CaO/TFe}PRESS最低,为690.1,说明拟合值与观测值之间偏差的度量小,模型的预测能力强,在估计真实回归系数和预测未来响应时较为精确且无偏倚。
3.3 异常值检验
采用模型对烧结矿RI进行分析时,会遇到许多偏离大部分评价数据的异常点,异常值会使得数据分布不均匀,若把它们与正常评价数据一同进行数据分析和模型训练,将会给模型训练带来不利影响[12-13]。为了检测出这些异常点,需对模型进行VIF、Durbin-Watson 统计量和 Grubbs检验[14],计算公式分别如式(5)~(10)所示。
式中,R2(Xj)表示将 Xj的判定系数作为响应变量,将模型中的其他项作为预测变量。
式中,d为误差距离;ei-1为第i个残差;ei为上一个观测值的残差;n为观测值个数。
Grubbs检验统计量的临界值P的单侧、双侧检验公式如式(9)和(10)所示。
式中,n为样本中的观测值个数;T代表服从自由度为n-2的t分布的随机变量。
根据Grubbs检验和Grubbs检验统计量的P值等诊断统计量,结果如表3所示。

表3 异常观测值的Grubbs检验Table 3 Grubbs Testing of Abnomal Observation Values
显著性水平0.05表示在实际上不存在异常值时得出存在异常值的风险为5%。由表3可知,Grubbs检验统计量的P值为0.044,小于显著性水平0.05,说明存在异常值。
删除异常值后, 建立 SiO2、MgO、TiO2、R、FeO和CaO/TFe与烧结矿RI之间的最优预测回归模型,如式(11)所示。
由式(11)可以看出,对烧结矿RI影响权重排序为 CaO/TFe、R、TiO2、SiO2、MgO 和 FeO。
对比删除异常值前后的回归结果,分析回归方程的统计量,结果如表4所示。

表4 删除异常值前后的回归结果对比Table 4 Comparison of Regression Results before and after Removing Abnomal Values
由表4可以看出,删除异常值前,MgO的P=0.054>0.05,TiO2的 P=0.108>0.05,效应均不显著。删除异常值后,重新建立回归模型,MgO的P=0.017<0.05,TiO2的 P=0.028<0.05, 均变成显著性因子。新模型的R2为99.88%,R2(调整)提高了0.02%,R2(预测)提高了 0.03%,S 降低了 0.222 6,模型预测更为精准。
3.4 预测结果分析
使用15个测试集对烧结矿RI回归预测模型进行评价,标准有以下3种:均方根误差RMSE,平均绝对误差MAE和平均相对百分比误差MAPE,如式(12)~(14)。
式中,f(xi)为烧结矿 RDI的预测值,yi为样本的实际值,n为样本预测个数。
利用三种评价标准结合15个测试集数据对烧结矿RI预测模型进行评判,结果如表5所示。

表5 预测模型评判Table 5 Judgment on Predictive Model
由表5可以看出,聚类分析方法在烧结矿还原性能预测方面有明显的优势。模型的均方根误差的 “边界值”为0.98,模型的均方根误差仅为0.975 0,预测值与实际值之间的偏差小。模型的平均绝对误差的“边界值”为0.85,模型的平均绝对误差为0.815 2,所有单个预测值与算术平均值的偏差绝对值的平均值小。模型的平均相对百分比误差的“边界值”为0.05,模型的平均相对百分比误差是0.015 3,绝对误差和预测值之间的平均值小。模型拟合效果好。
模型的预测值与真实值对比如图3所示。由图3可以看出,烧结矿RI回归模型的预测值与实验值吻合良好,预测值与实验值数据点更贴近理想45°线,预测结果较为精准。
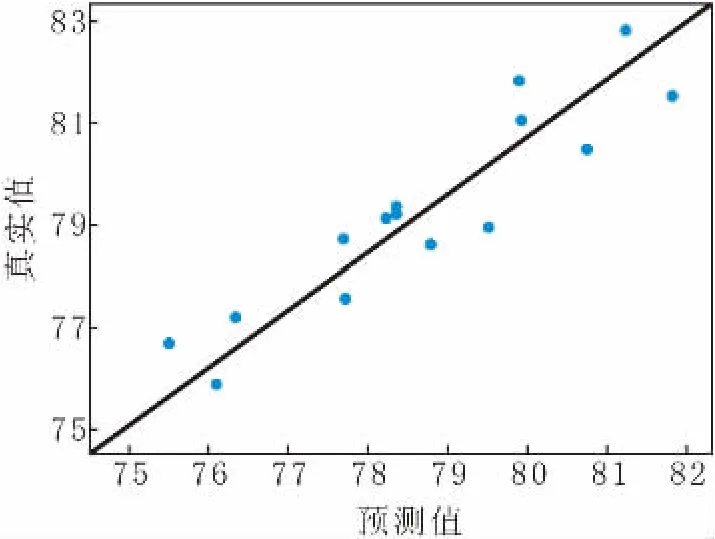
图3 模型预测值与真实值对比Fig.3 Comparison of Values by Model Prediction and True Values

图4 模型相对误差Fig.4 Relative Errors of Model
4 结论
(1)选取12个影响烧结矿RI的因子并进行变量聚类,选择相关性小且具有代表性的SiO2、Al2O3、MgO、S、TiO2、R、FeO 和 CaO/TFe 共 8 个 因子反映对烧结矿RI的影响。
(2)最佳子集回归得到影响烧结矿RI的最主要因素为 SiO2、MgO、TiO2、R、FeO 和 CaO/TFe 共6个因子,利用 VIF、Durbin-Watson统计量和Grubbs检验异常值,建立预测回归模型,即RI=13.61w(SiO2)-6.47w(MgO)-19.2w(TiO2)+37.03w(R)-2.91w(FeO)-190.9[w(CaO)/w(TFe)]。
(3)模型的R2达到99.88%,模型拟合效果好,相对误差均在3%以下。模型预测值与实验值数据点更贴近理想45°线,验证了模型的实用性,能够快速有效地预测烧结矿RI。
