大管径管道冰浆流动阻力特性实验研究*

唐道轲 付 林 杨 波 李永红 李建刚

(1.清华大学,北京;2.北京航空航天大学,北京;3.太原市热力集团有限公司,太原)

0 引言

作为冷冻法的一种,动态制冰在水处理领域已有一定的研究和应用,包括废水再生[1]和海水淡化[2]。动态制冰法通常利用过冷解除、真空闪蒸等技术,直接在流动的水中生成细小的冰晶颗粒,形成流态的冰水混合物,即冰浆。水在结冰过程中,盐分和杂质会被自动排除在冰晶之外,再经过洗涤、分离、融化等一系列过程,最后就能得到较为纯净的淡水。而在此之外,冰浆在区域供冷领域有着更广阔的应用前景[3-5]。一方面蕴含着可观的潜热,另一方面还具备流动性。冰浆是非常理想的供冷介质,尤其是制备过程中可以利用峰谷电价差[6]或跨季节废热。冰浆供冷是实现低碳、高效供冷的有效途经之一。

冰浆应用不可避免要涉及输送问题。冰浆属于固液两相流,当含冰率超过一定值时,冰浆会表现出非牛顿流体特征,即剪切应力与速度梯度不再成正比,其阻力特性相较于单相流更为复杂。目前,主要有4种流变模型用来描述冰浆的非牛顿流体特征,包括Bingham、Casson、Power Law、Herschele-Bulkley等[7]。有研究表明,Herschele-Bulkley模型与实验结果最为接近,但最大偏差也会达到30%以上[8]。

刘永红等人针对管径为8.83 mm的光滑铜管开展实验研究,发现在低流速下冰浆阻力比纯水大,而在高流速下则与含冰率密切相关,含冰率在2%～30%以下时冰浆阻力反而比纯水小,这可能与冰浆的再层流化有关,冰晶的存在会抑制层流向湍流的转化[9]。王继红等人采用Power Law流变模型来描述冰浆层流流动,即壁面剪切应力与剪切速度满足指数关系,实验发现,随着含冰率(10%～25%)和管径(DN25和DN40)增大,流变系数K增大,而流变指数n则减小且始终大于1[10]。Illan等人发现在低雷诺数下含冰率越大则阻力越大,且显著大于纯水,而在高雷诺数下冰浆的阻力系数曲线基本与单相的Blasius线重合,而与含冰率无关,实验中的管径在16.1～35.7 mm之间,含冰率在5%～26%之间[11-12]。Bordet等人利用可视化手段对冰浆流动型态进行了归类,实验工况覆盖了从纯水到18.4%含冰率,也发现了与文献[11-12]相似的阻力特性变化规律[13]。需要指出的是,以上研究中,前3个采用的都是质量含冰率,Bordet等人采用的则是体积含冰率,而本研究采用的也是体积含冰率。

从目前检索到的文献来看,现有研究或受限于实验条件,或由于面向的应用规模较小,冰浆输送管道多是在管径50 mm以下,而且更多是在10～30 mm,流动多属层流或低雷诺数湍流,对于更大管径、更高雷诺数的研究和应用则很少看到,而未来大规模的水处理和区域供冷应用必然需要更大的冰浆输送能力、更大的输送管径。已有研究指出,管径对冰浆流动特性影响显著,在小管径下,近壁面升力和湍流扩散力的影响效应能覆盖较大的管高范围,而大管径下这些动量传递机制的影响范围有限,更容易出现非均质流[14-15]。因此,有必要针对大管径输送开展冰浆流动阻力特性研究,填补现有研究的空白。

1 冰浆阻力特性实验台

本文针对DN50(内径52 mm)和DN80(内径78 mm)2种大管径的无缝钢管开展冰浆流动阻力特性实验研究。冰浆阻力实验台如图1所示,实验所用冰浆由1台吸收式真空制冰机提供,存放在1个带搅拌器的罐子中,通过调节搅拌器转速可以改变输送出去的冰浆含冰率,冰浆由浆体泵抽出送入测试段,最后回到搅拌罐。测试段包含DN50和DN80 2段并联的3 m长直管路,可通过阀门进行切换,DN50和DN80测试段末端都设置有透明有机玻璃管,用于观察冰浆流型。

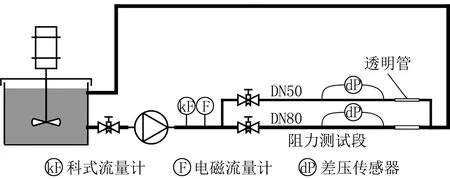
图1 冰浆阻力实验台

冰浆的质量流量由科式流量计测量,科式流量计还可以在线测量冰浆密度,由此可计算出含冰率。此外,实验台还设置了电磁流量计以测量冰浆的体积流量。实验发现,电磁流量计直接测量的体积流量与科式流量计经密度换算后得到的体积流量相差无几,这表明电磁流量计仍适用于冰浆的体积流量测量。这为实际工程应用提供了冰浆测量的廉价方案,即可以用电磁流量计搭配在线密度计来测量冰浆流量和含冰率,以替代昂贵的科式流量计。阻力测量采用差压传感器,为尽可能消除水力入口效应的影响,差压传感器的高压测点距离直管入口1.5 m,满足湍流水力入口段长径比10的要求[16]。测量段长度为1 m,小流量下阻力可能只有数百Pa,而大流量下又会达到数千Pa,为应对不同流量,实验准备了500 Pa和5 000 Pa 2种量程的差压传感器。

实验所用的仪器参数见表1。

表1 实验仪器参数

2 结果与讨论

2.1 DN50管阻力特性

DN50管的实验获得了2组稳定的含冰率,分别为8%和16%,对应冰浆密度分别为987 kg/m3和993 kg/m3。在每组含冰率下,通过浆体泵变频获得不同的流量。在8%含冰率实验组中,体积流量从9.51 m3/h逐步增大至27.17 m3/h,流速从1.24 m/s增大至3.55 m/s,雷诺数从36 111增大至103 135,相应地,比摩阻从392 Pa/m增大至2 113 Pa/m,阻力系数从0.026 6降至0.017 7。在16%含冰率实验组中,体积流量从10.3 m3/h逐步增大至27.73 m3/h,流速从1.35 m/s增大至3.63 m/s,雷诺数从39 089增大至105 246,比摩阻从425 Pa/m增大至2 211 Pa/m,阻力系数从0.024 5 降至0.017 6。

当实验进行较长时间后,搅拌罐中的冰晶已融化殆尽,最后只剩下0 ℃的水,借此条件又测试了0 ℃水的阻力特性,以与冰浆实验结果及单相流阻力关联式进行对照。实验测试中水流量从7.47 m3/h逐步增大至27.81 m3/h,比摩阻从233 Pa/m增大至2 183 Pa/m,阻力系数从0.025 4降至0.017 2。

本实验涉及的流动形式均为湍流。对于光滑管,单相湍流流动的阻力系数满足Blasius关联式:

f=0.316Re-0.25

(1)

式中f为阻力系数;Re为基于载流体(即0 ℃水)物性计算的雷诺数,有些文献将其命名为参考雷诺数(reference Reynolds number)。

对于粗糙管,适用Colebrook关联式:

(2)

式中ε为绝对粗糙度,mm,按新管取值0.01 mm;D为管径,mm。

这2个关联式都适用于Re>4 000的湍流光滑区,前者在Re<105具有较高精度,后者还可以拓展到湍流过渡区和湍流粗糙区[17]。

在工程应用中,比摩阻s(即单位流动长度的压降)能更直观地反映沿程阻力特性,它与阻力系数的关系如下:

(3)

式中ρ为流体密度,kg/m3;u为流速,m/s。

将以上0 ℃水、8%冰浆、16%冰浆的实验结果绘制在图2、3中,并与2个关联式计算结果进行对照,其中,关联式的计算是基于0 ℃水的物性。从图2来看,水及2种含冰率下冰浆的比摩阻实验结果都与Blasius曲线吻合得很好,而Colebrook曲线在高雷诺数下逐渐偏离Blasius曲线。从图2的比摩阻数据中很难看出各实验组阻力特性之间的差异,图3的阻力系数则将这种很小的差异进行了放大。由图3可以看到,在低雷诺数下,冰浆的阻力系数明显大于水,而且含冰率越高,阻力系数越大,在这一区域,水的数据点仍基本落在Blasius曲线上,而冰浆的数据点明显偏离Blasius曲线。

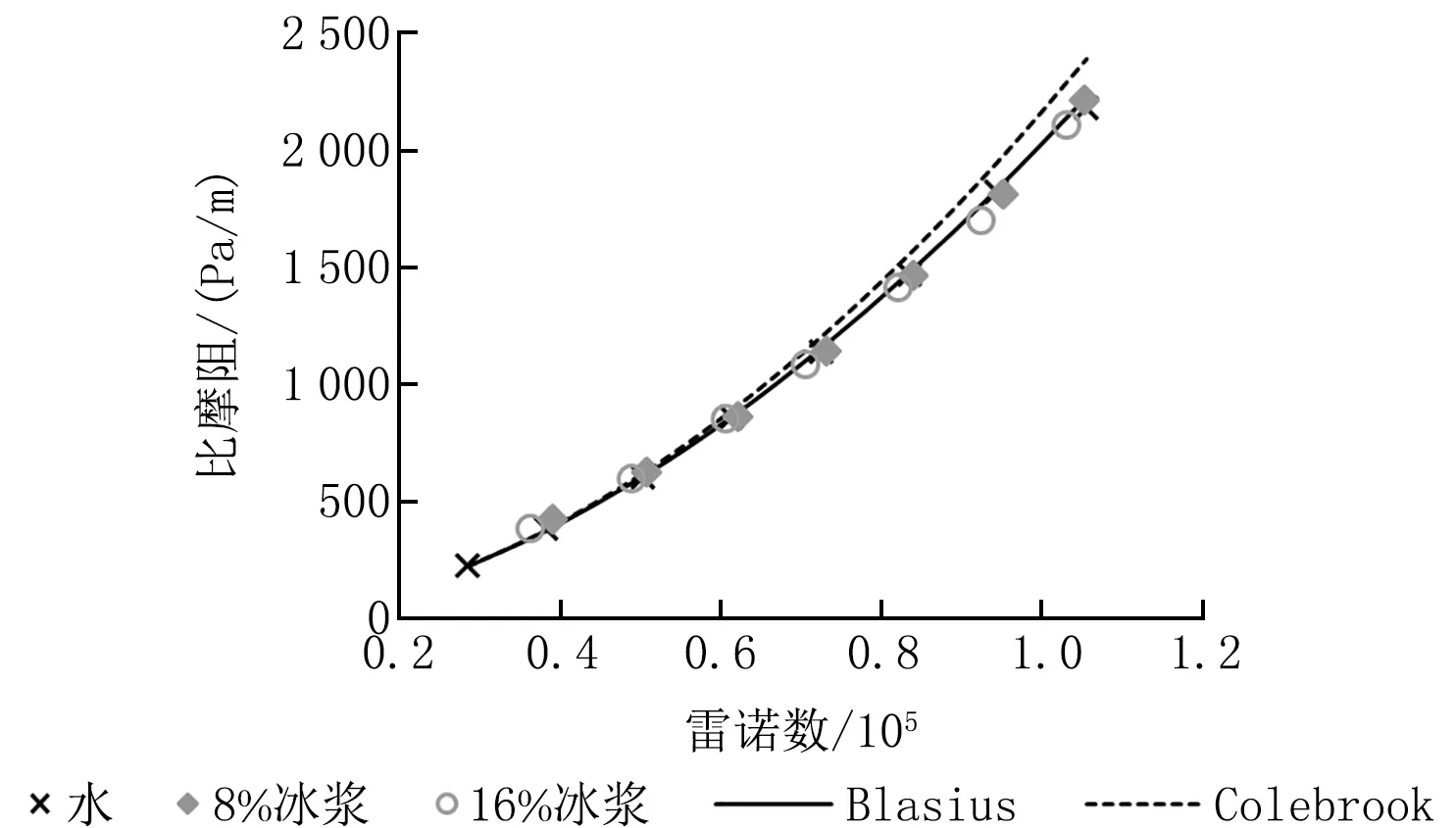
图2 DN50管比摩阻与雷诺数的关系

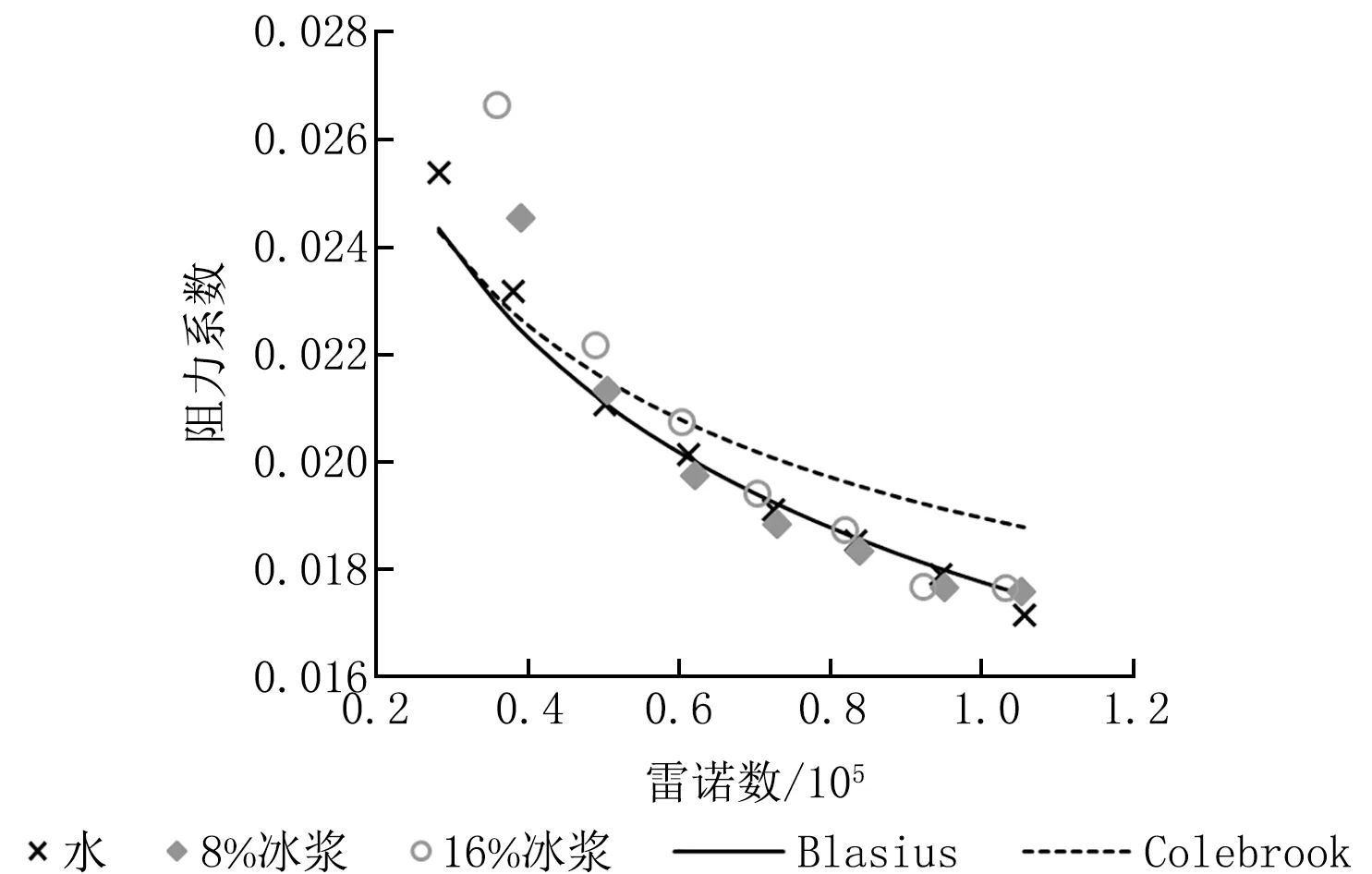
图3 DN50管阻力系数与雷诺数的关系

由于实验得到的是离散点,为了定量判断冰浆阻力系数何时进入Blasius曲线,本文对实验数据进行了拟合,获得了不同含冰率下冰浆阻力系数与雷诺数的指数关系式。

含冰率8%:

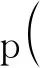
(4)

含冰率16%:

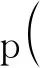
(5)

拟合相关系数分别为0.996 92和0.990 06。将以上拟合结果绘制成曲线,如图4所示。以阻力系数偏差小于5%作为判定标准,8%和16%冰浆分别在雷诺数为4.47×104和5.16×104时其阻力系数开始进入Blasius曲线。

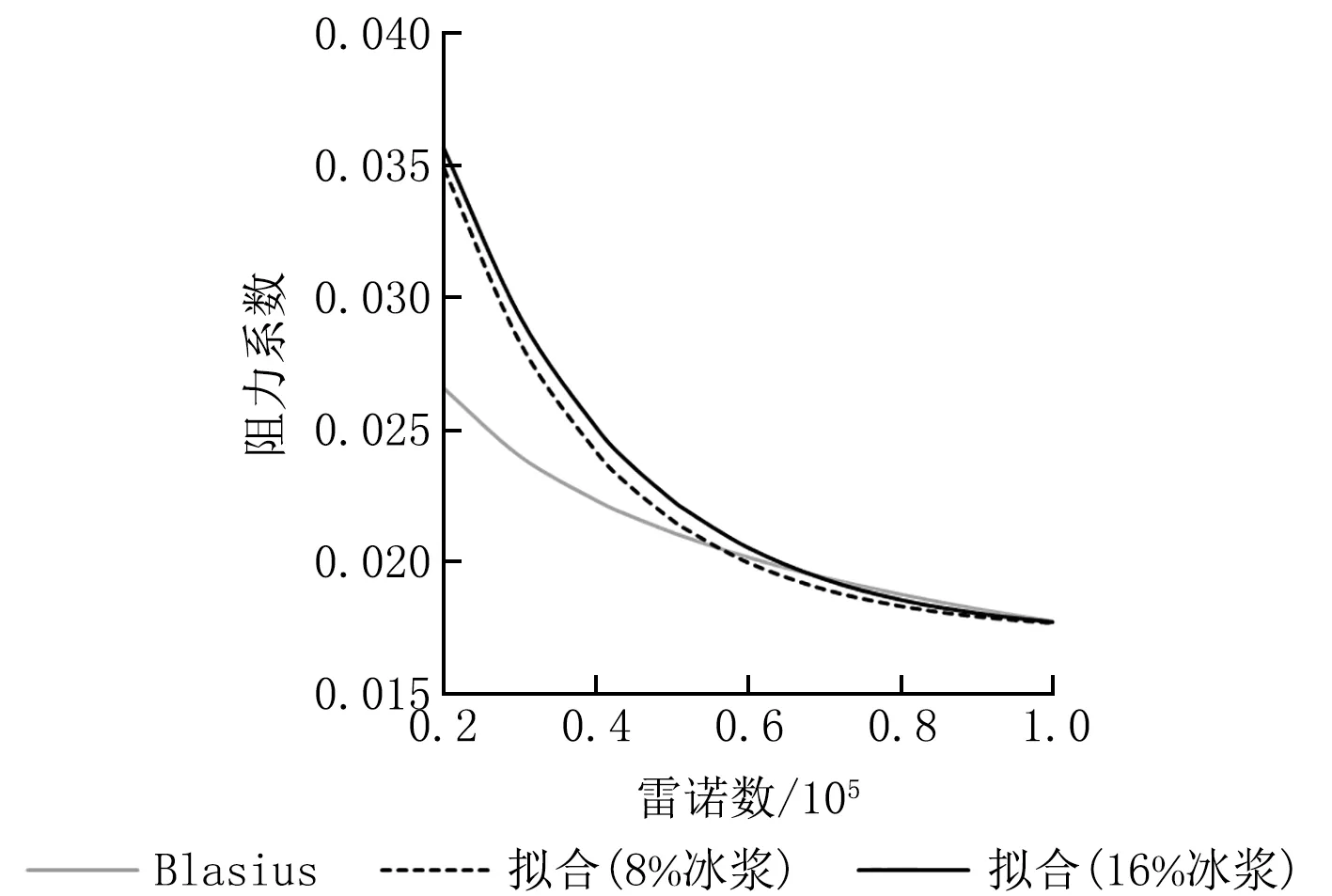
图4 DN50管的冰浆阻力系数拟合曲线

2.2 DN80管阻力特性

在DN80管的实验中,获得了2组稳定的含冰率,分别为6%和13%,对应的冰浆密度分别为995 kg/m3和989 kg/m3。实验结果见图5、6。本组实验中,雷诺数大部分都在5.00×104以上,最高达到1.32×105。从图5、6可以看到:无论是比摩阻还是阻力系数,Colebrook曲线都与实验数据点及Blasius曲线偏离显著;与DN50管一样,水的数据点仍与Blasius曲线吻合得很好;在低雷诺数(5.00×104以下)下,冰浆的阻力系数远高于Blasius曲线,而随着雷诺数增大,各组含冰率的阻力系数都逐渐落入Blasius曲线。

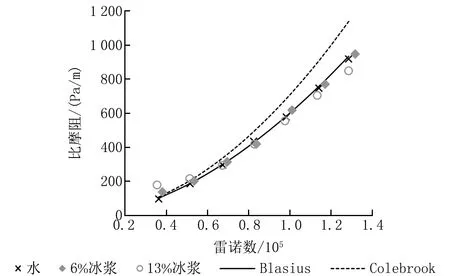
图5 DN80管比摩阻与雷诺数的关系

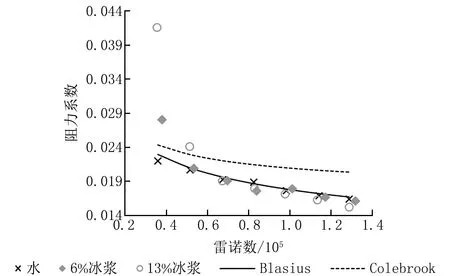
图6 DN80管阻力系数与雷诺数的关系

将DN80管的冰浆阻力系数实验数据拟合成指数关系式。

含冰率6%:

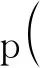
(6)

含冰率13%:

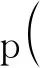
(7)

拟合相关系数分别为0.975 56和0.993 23。将以上拟合结果绘制成曲线,如图7所示。仍以阻力系数偏差小于5%作为判定标准,6%和13%冰浆分别在雷诺数为5.13×104和5.81×104时其阻力系数开始进入Blasius曲线。

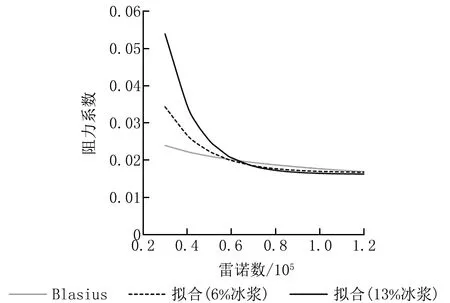
图7 DN80管的冰浆阻力系数拟合曲线

2.3 直管阻力实验结果分析

综合以上实验与关联式对照结果,可以得出结论:在低雷诺数(但仍是湍流)下,冰浆的阻力系数远大于水的阻力系数(亦即Blasius计算值);在高雷诺数下,冰浆的阻力系数基本与水一致,与Blasius曲线吻合。这可以解释为:在低雷诺数下,冰浆流动呈现出固液两相分层流的特征,浮力相较于惯性力而言占主要部分,更多的冰晶颗粒悬浮在管道上部,冰晶与上壁面碰撞频繁,故而阻力显著大于水;在高雷诺数下,冰浆表现为均质流,冰晶较为均匀地悬浮在整个截面,冰晶与壁面碰撞频率较低,此时冰浆的流动与单相流基本无异,故与单相流的Blasius曲线吻合。

关于冰浆阻力系数何时开始进入Blasius曲线,从实验结果来看,含冰率越大则进入Blasius曲线时的雷诺数越大,这与文献[11]中的实验数据是一致的,如图8a所示。至于不同管径,由于本研究中DN50管和DN80管实验的含冰率并不一致,前者是8%和16%,后者是6%和13%(含冰率均低于前者),前者进入Blasius曲线的雷诺数分别为4.47×104和5.16×104,后者则是5.13×104和5.81×104。由此可以推断,管径越大则越晚进入,这也与文献[11]中的实验数据一致,如图8b所示。文献[11]中涉及的管径最大为35.7 mm,在最高26%的含冰率下,进入Blasius曲线的雷诺数大约为3×104。

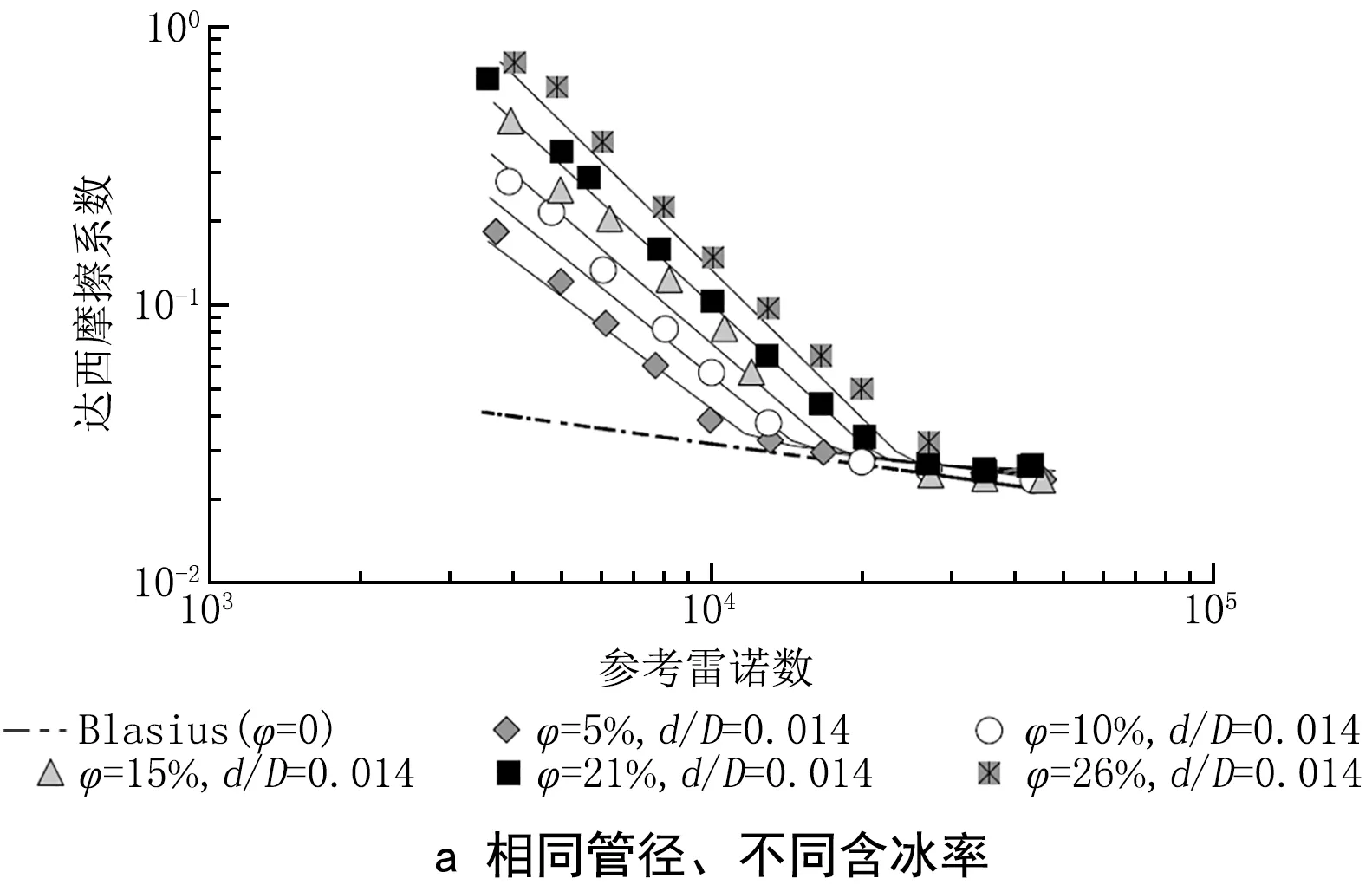
注:φ为含冰率;d为冰晶粒径(0.5 mm)。

2.4 冰浆堵塞实验结果与分析

冰浆在低流速下容易形成分层,冰晶颗粒上浮而聚集,最后形成静止床而造成管道堵塞,这是冰浆应用的最大障碍。通常,直管只要保证一定流速就能避免堵塞。在实验中,测试的直管段始终未出现堵塞的情况,这也符合Bordet等人给出的直管临界流速建议[13]。然而,对于弯头而言,由于固液离心力差异,冰浆更容易形成分层而造成堵塞。由于实验管路是一个环路,管路中正好设有90°DN80弯头,故本文借此条件对弯头的堵塞特性进行了研究。通过不断调小流量,找到从畅通到开始出现堵塞的临界流速,判断堵塞的依据则是流量出现剧烈波动。按照该方法,实验获得了弯头在不同含冰率下的临界流速,如图9所示。由图9可见,含冰率越大,则临界流速越大,临界流速与含冰率近似呈线性关系。另外,实验还发现,在弯头出现堵塞的流速下,直管仍是畅通的,验证了弯头更容易堵塞。

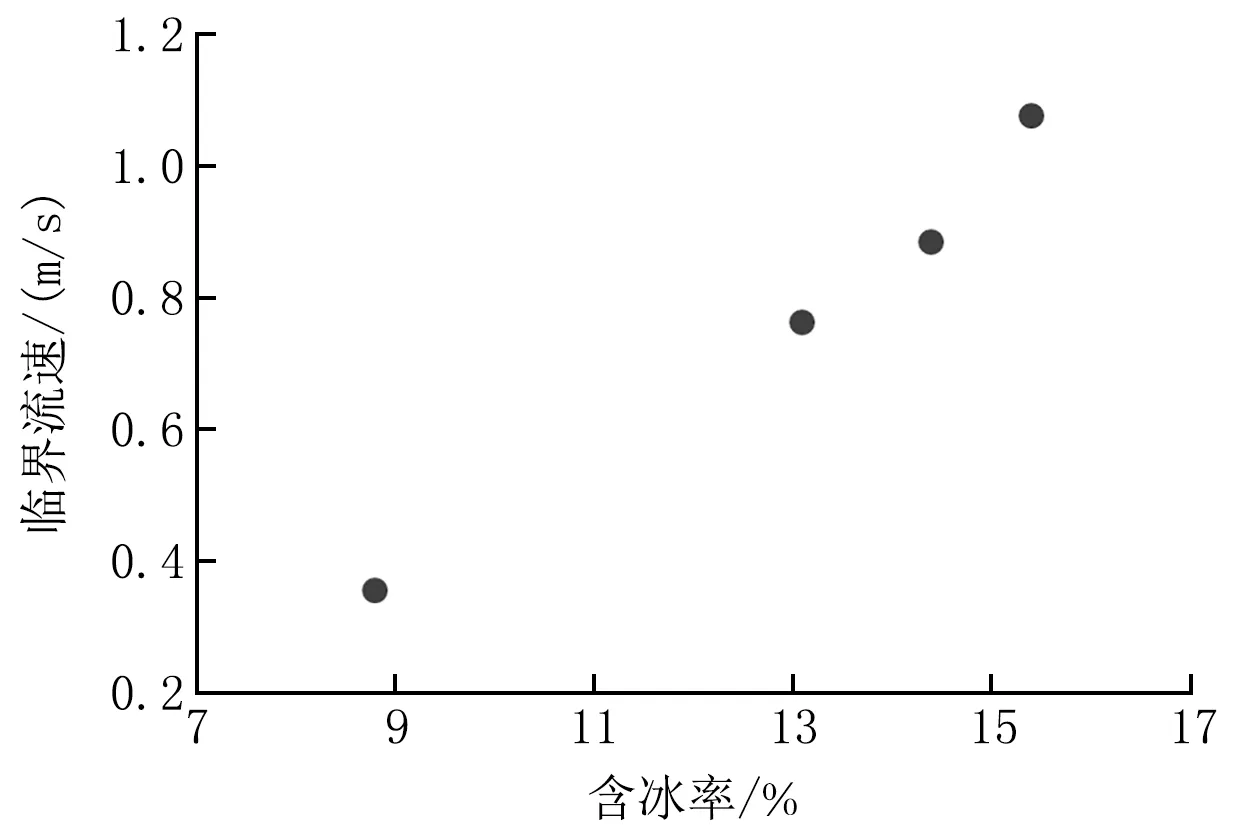
图9 弯头的临界流速与含冰率的关系

3 结论

本文针对DN50和DN80 2种大管径管道开展了冰浆流动阻力特性实验研究,实验均处于湍流。得到以下结论:

1) 在低雷诺数下,冰浆阻力系数远大于适用于纯水单相流的Blasius关联式计算值,且含冰率越大,阻力系数越大。

2) 在高雷诺数下,冰浆的阻力特性符合Blasius关联式,不同含冰率下的阻力系数都与纯水一致。

3) 含冰率和管径对冰浆阻力系数何时进入Blasius曲线有影响,含冰率越大、管径越大,则开始进入Blasius曲线的雷诺数越大。

4) 相较于直管,弯头的临界流速更高,更容易出现堵塞,且含冰率越大,则临界流速越大。

本文的研究可为DN50～DN80级别的大管径管道冰浆输送提供技术参考,从目前实验结果所反映的规律来看,本文的研究结论可拓展到更大管径,在更大的管径下,冰浆流动即使在不大的流速下也能达到很大的雷诺数,阻力特性符合Blasius关联式。考虑到搭建更大尺度的实验台具有一定难度,现计划开展CFD研究,以本文的实验结果验证或修正固液两相流模型,而后针对更大管径的冰浆流动开展CFD仿真,这将是下一步的研究工作。