基于CarSim仿真软件的匝道路面摩擦系数研究

黄晓明,刘泽宇,洪正强

(1. 东南大学 交通学院,江苏 南京 211189; 2. 国家道路与交通工程实验教育示范中心,江苏 南京 211189;3. 中国建筑工程(香港)有限公司,中国 香港 999077)

0 引 言

匝道是道路不可缺少的组成部分,承担着衔接主辅路、互通相交道路及引导行车路线等任务,一般由圆曲线和缓和曲线组成,属于小半径曲线路段。车辆驶入匝道时往往需要经历明显的减速与转向阶段,容易发生侧滑、失稳甚至侧翻[1]。导致匝道发生事故的因素主要有:①驾驶员的驾驶习惯及心理判断,此乃主观因素,暂不作研究;②道路状况不佳,包括道路设计参数不合理和路面病害,为客观因素,其中,既有匝道的平、纵、横3要素均无法改变,而坑槽、车辙等路面病害通常使司机降低车速,因此,难以被司机察觉的路面抗滑不足成为影响既有匝道上车辆行驶安全的首要客观因素[2]。车辆以较高速度驶入匝道时,若路面抗滑性能不足,将导致轮胎与路面接触减弱,轮胎产生不易察觉的滑动,这种隐患直至当车辆制动、转向失去稳定时才会被驾驶员察觉,且该隐患在雨天和小半径曲线路段尤为严重[3-5]。因此,判断抗滑性能是否满足要求是匝道车辆安全行驶的首要任务。

目前,业内主要通过直线路段制动试验的结果来评价道路抗滑性能,由此得到的摩擦系数阈值是否适用于形如匝道的小半径曲线路段尚不清楚,因此,有必要开展研究。

CarSim是一款车辆动力学软件,可根据动力学理论利用该软件对车辆进行建模,并通过外接MATLAB/Simulink端口进行仿真模拟,因此,CarSim广泛应用于车辆行驶稳定性研究。赵树恩等[6]建立了包含侧向、横摆和侧倾运动的3自由度侧翻动力学模型,基于差动制动进行数字仿真,提出融合动态载荷转移率和车辆横摆角速度的差动制动防侧翻主动控制策略;洪正强等[7]建立了车辆和路面模型,基于车辆行驶稳定性进行模拟试验,确定了不同车速、不同路段及不同干湿程度下的路面车辙阈值;石沛林等[8]结合实际交通事故的制动距离影响因素,利用CarSim仿真得到一种以最大制动加速度持续时间为自变量的制动初速度计算公式。

笔者基于CarSim仿真软件,对不同条件匝道路面摩擦系数阈值进行研究。首先,建立车-路模型并设计2种行驶工况,选取并确定车辆行驶状态评价指标;然后,进行仿真试验,得到不同工况下匝道车辆的行驶数据;最后,分析提出基于车速-坡度二元因素的匝道路面摩擦系数预测公式。

1 基于CarSim的车-路模型

1.1 车辆动力学建模

应用CarSim建立车辆模型,采用D-Class Sedan小轿车模型进行仿真模拟。小轿车模型具体物理参数见表1(采用该车型默认设置),轿车为前轮驱动,六档自动变速。

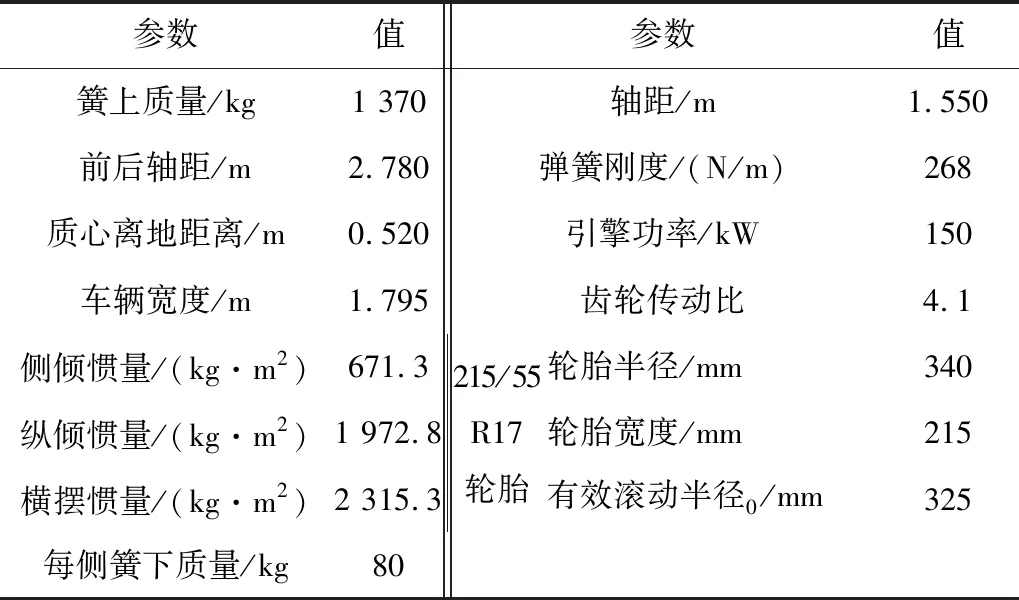
表1 小轿车模型物理参数

1.2 匝道模型建立

鉴于高速公路出口匝道最容易发生交通事故[9],因此笔者主要研究高速公路出口匝道模型。根据《中华人民共和国道路交通安全法实施条例》,不得在匝道上超车,一般也不能变道,大部分匝道要求车速低于40 km/h。因此,限速标准选取40 km/h,根据JTG D 20—2017《公路路线设计规范》建立匝道模型。

1.2.1 匝道平曲线

选取最不利工况的圆曲线半径R=50 m;匝道缓和曲线参数A=35 m,长度Ls=35 m。根据平曲线要素,参考JTG/T D 21—2014《公路立体交叉设计细则》,匝道设计为环形。

1.2.2 匝道纵坡

当匝道设计速度为40 km/h时,纵坡坡度i=5%～-4%,由此分别建立常坡度i=5%、2%、0%、-1%、-2%、-3%和-4%的竖曲线模型,重点观察下穿匝道。

1.2.3 匝道横断面

一般高速公路的路拱横坡为2%;圆曲线半径为50 m的匝道加宽值为0.5 m,在曲线内侧进行;车道宽度3.5 m;最大超高6%;超高过度旋转轴为弯道内侧,超高渐变率为1/100。经检查,合成坡度均小于10%,满足规范要求。

1.3 驾驶员模型建立

每个驾驶员都有自己的驾驶习惯,笔者所建驾驶员模型的核心参数是制动感知反应时间,即从驾驶员意识到前方道路上存在需要制动的障碍物到驾驶员实际应用制动器的时间间隔。目前,基于直线路段试验得出的制动反应时间一般是2.5 s[10],但是在匝道路段行驶时,司机会更加集中注意力,制动反应时间也会缩短,因此,笔者选择2 s作为驾驶员模型中的制动反应时间。此外,车辆全程保持匀速行驶,以道路中线为基本行驶路线,自动纠偏,因此,不对驾驶员制动模型作出修改,采用默认设置。

1.4 行驶工况设计

设计2种典型行驶工况,其滚动阻力系数均为1.5,即默认均为沥青路面。

1)工况1——不同速度下正常行驶

设定初始路面摩擦系数为 0.75(即干燥沥青路面),在40 km/h限速的基础上,分别计算超速10%、20%、30%、40%和限速70%、80%、90%等情况的车辆行驶状态。基于以上设定找出车辆能够正常行驶的情况。

2)工况2——不同速度下制动

在工况1的基础上,选取制动主缸压力P=0～10 MPa,间隔为1 MPa;制动起始位置为驶入匝道并保持稳定行驶状态时的位置;除考虑刹车制动,也将发动机气缸自身的制动性能考虑在内;所有车型均配备ABS系统。基于以上设定观察车辆制动时的情况。

2 车辆行驶状态评价指标

影响车辆行驶状态的因素有很多,但不论是什么因素,最终都会反映在某些具体指标或人体主观感受上,即车辆行驶状态包括车辆的安全性和稳定性以及乘车人的舒适性。

2.1 评价指标选取

根据GB/T 6323—2014《汽车操纵稳定性试验方法》,评价车辆稳定性的主要指标有侧向加速度ay、横摆角速度ω及制动减速度(即纵向加速度)ax,这3个指标均可被乘客直观感受,即舒适性指标,对车辆的行驶状态起着决定性作用。

此外,还有一些实际行驶时才会遇到的安全性指标,即制动距离d和侧向偏移距离l,及判断车轮是否会发生侧滑的重要指标——峰值附着系数μmax。不过,这3个指标均无法直接被乘客感受。

2.2 指标限值确定

2.2.1 侧向加速度ay

侧向加速度ay是行车舒适性评价指标。根据GB/T 6323—2014,对于总质量不超过2.5 t的轿车、客车和货车,ay≤9.8 m/s2,这个限制条件可保证行驶安全性,但不能保证驾乘人员的舒适性。

2.2.2 横摆角速度ω

横摆角速度ω是行车舒适性评价指标,一般采用侧向加速度-车速(ay-V)法计算。对于做匀速圆周运动的汽车,ω可由式(1)计算:

(1)

2.2.3 制动减速度ax

制动减速度ax是行车舒适性评价指标。若车辆在制动同时发生转向或紧急避让动作,制动减速度会影响侧向加速度,也会影响乘客乘车感受,引发驾驶员的心理变动。根据S. MOON等[11]和郑彬双[12]的研究,驾驶员的制动行为受车速的影响较大。

汉斯·洛伦茨[13]、XU Jin等[14]研究得出了ay的指标阈值,由其可计算出ω、ax的指标阈值,见表2。

表2 侧向加速度ay、横摆角速度ω、制动减速度ax的指标阈值

2.2.4 制动距离d

制动距离d是行车安全性评价指标。根据JTG D 20—2017,匝道设计速度为40 km/h时,制动距离d需满足d≤40 m。若制动距离在规定范围内,则行车安全性判定为“安全”;若制动距离超出规定范围,则行车安全性判定为“危险”。

2.2.5 侧向偏移距离l

侧向偏移距离l是行车安全性评价指标。规定行驶在车道中线的车辆侵占任意一侧相邻车道时的侧向偏移距离为“一般值”,而行驶在靠某侧边线的车辆侵占另一侧相邻车道时的侧向偏移距离为“极限值”,如图1。

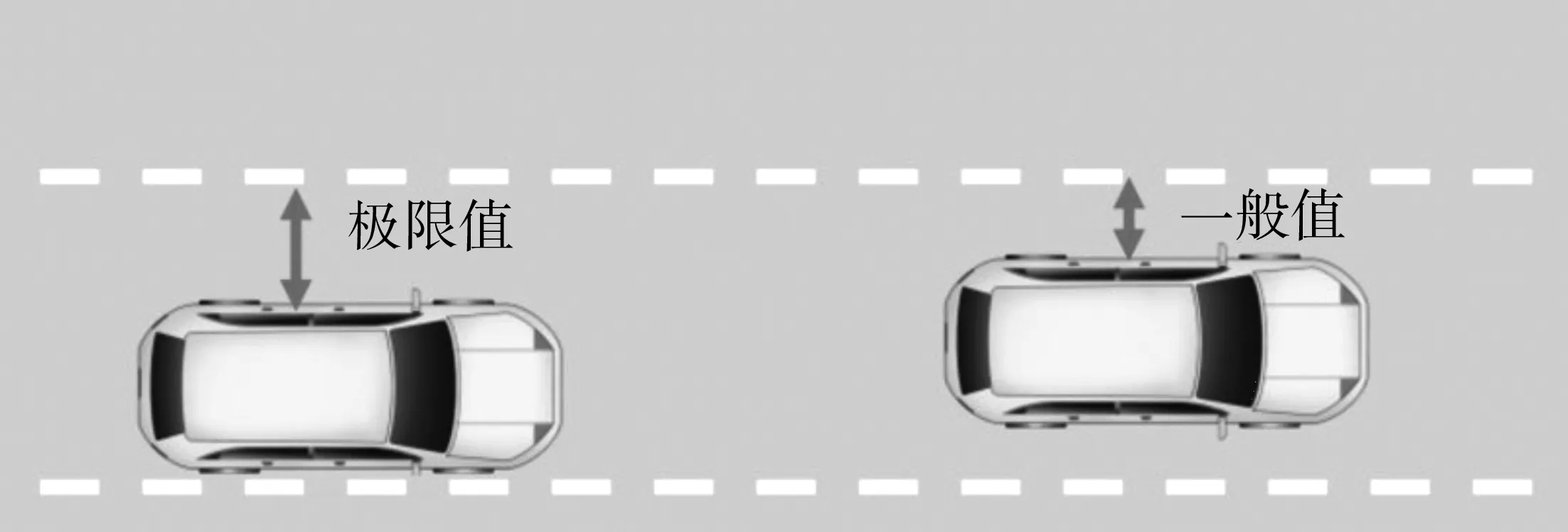
图1 侧向偏移距离一般值和极限值

根据表1,模型车辆宽度为1.795 m,保守起见,取2 m。匝道宽度为3.5 m,加宽0.5 m,因此在不侵占相邻车道的前提下,最大侧向偏移距离一般值为1 m,极限值为2 m。若侧向偏移距离在一般值范围内,则行车安全性判定为“安全”;若超出一般值,但是在极限值范围内,可以通过调整驶入位置保证安全,行车安全性判定为“存在风险”;若超出极限值,行车安全性判定为“危险”。

2.2.6 峰值附着系数μmax

峰值附着系数μmax是行车安全性评价指标。若μmax达到路面摩擦系数μ0,则车轮开始侧滑,极易发生事故。因此,峰值附着系数μmax的阈值应为路面提供的摩擦系数值。

笔者预设5种路面摩擦系数值,分别为0.75(干燥)、0.55(潮湿)、0.40(积水)、0.30(雪天)以及0.20(结冰)。通过μmax图可以得到车辆在不同行驶状态下能够适应的最恶劣路面条件(此时路面摩擦系数最小,为路面最低摩擦系数μ0,min)。

3 匝道路面摩擦系数仿真试验

基于所建的模型和设置的评价指标,在CarSim仿真软件中开展模拟试验,观察车辆的行驶状态。

3.1 工况1,i=5%

图2为车辆的行驶数据,反映了ay、ω、l和μmax随行程变化的情况。

图2 纵坡i=5%上穿匝道工况1的车辆行驶状态

由图2可见:

1)遵守限速和超速10%(即V=40、44 km/h)时,在弯道路程ay=(1.8,3.6] m/s2,属于较舒适状态;超速20%(即V=48 km/h)时,ay,max=3.7 m/s2,属于一般状态并持续56.3 m,其余弯道路程均处于较舒适状态;超速30%(即V=52 km/h)时,在弯道路程ay=(3.6,5.0] m/s2,属于一般状态;超速40%(即V=56 km/h)时,ay,max=5.1 m/s2,属于不舒适状态并持续42.1 m,其余弯道路程均处于一般状态。

2)遵守限速和超速10%(即V=40、44 km/h)时,在弯道路程ω=(372/V,744/V] (°)/s,属于较舒适状态;超速20%和超速30%(即V=48、52 km/h)时,ω=(744/V,1 032/V] (°)/s,属于一般状态;超速40%(即V=56 km/h)时,ω>1 032/V(°)/s,属于不舒适状态。

3)遵守限速至超速20%(即V=40、44、48 km/h)时,在行驶全过程侧向偏移距离l均处在安全范围内;超速30%和超速40%(即V=52、56 km/h)时,驶入匝道时l处在安全范围内,驶出匝道时l严重超出一般值,且内外偏移量绝对值之和超出极限值,无法通过调整驶入位置来保证行车安全。

4)遵守限速和超速10%(即V=40、44 km/h)时,μmax<0.30,表示车辆能够在雪天正常行驶;超速20%(即V=48 km/h)时,μmax<0.40,表示车辆能够在有一定积水的路面行驶;超速30%和超速40%(即V=52、56 km/h)时,μmax<0.55,表示车辆能够在潮湿的路面上行驶。车速V=40、44、48 km/h时,车辆正常行驶的路面最低摩擦系数μ0, min分别为0.23、0.29和0.36。

3.2 工况2,i=5%

选定不同车速进行制动试验,速度条件分别为:40 km/h(限速)、44 km/h(超10%)和48 km/h(超20%),在满足制动安全距离要求的前提下,寻找舒适性最高的制动方式。

3.2.1V=40 km/h时车辆制动情况

根据工况1的试验,设定此时路面摩擦系数μ0=0.23,图3为车辆的行驶数据,反映了ax、d、l和μmax随时间变化的情况。

图3 纵坡i=5%上穿匝道工况2V=40 km/h, μ=0.23的车辆制动情况

由图3可见:

1)主缸压力P=1 MPa时,ax≤2 m/s2,曲线随时间发生的变化比较缓和,属于舒适状态,但整体制动时间较长;P=2～10 MPa时,ax=(2,4] m/s2,属于较舒适状态。

2)P=1～10 MPa时,d> 50 m,无法达到40 m的要求,曲线随着主缸压力升高,制动距离并不会减少。

3)P=1 MPa时,l在行驶全过程均处在安全范围内;P=1～10 MPa时,随着P的升高,l越来越大,但内外偏移量绝对值之和均未超出极限值,因此,可以通过调整驶入位置来保证行车安全。

4)P=1 MPa时,μmax较为稳定;P> 1 MPa时,μmax出现了非常明显的波动,P>3 MPa时,μmax>0.23,此时路面摩擦系数无法满足轮胎的需求。

针对其他预设的路面摩擦系数μ0=0.30、0.40、0.55、0.75,分析方法相同,为节约篇幅,不赘述,仅列出研究结论:

1)P=1～2 MPa时,无论何种路面抗滑条件,均无法满足制动安全距离要求。

2)μ0=0.30时,任何制动方式都无法满足制动安全距离要求。

3)μ0=0.40、0.55时,若P=3～10 MPa,则d<40 m,ax=(4,6] m/s2,属于安全且舒适性一般制动情况。

4)μ0=0.75时,若P=3 MPa,则d<40 m,ax=(4,6] m/s2,属于安全且舒适性一般制动情况;若P=6 MPa,则d<40 m,ax=(6,8] m/s2,属于安全且不舒适制动情况;若P=10 MPa,则d< 40 m,ax> 8 m/s2,属于安全且极不舒适制动情况。

5)μ0=0.36时,若P=6 MPa,则d< 40 m,ax=(2,4] m/s2,属于安全且较舒适的制动情况,则路面最低摩擦系数U0,min=0.36。

3.2.2 不同车速下的车辆制动情况

同理,对于在纵坡i=5%上穿匝道工况2条件下行驶的车辆,笔者总结了不同车速下满足安全性条件的最佳制动情况,结果如表3。

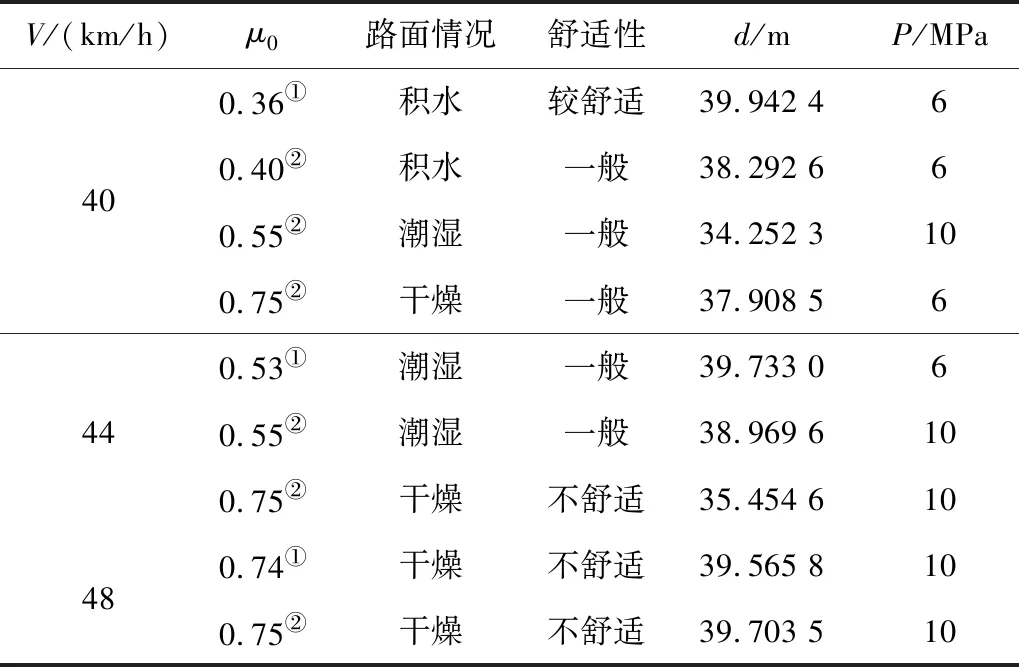
表3 纵坡i=5%上穿匝道工况2的车辆制动情况

3.3 其他坡度匝道路面摩擦系数仿真试验

按照同样的方法,分析匝道坡度i=2%(上穿)、0%(平面)、-1%(下穿)、-2%(下穿)、-3%(下穿)和-4%(下穿)各种工况下的匝道路面摩擦系数。为节约篇幅,略去了具体数据和分析过程,试验结果见表4。

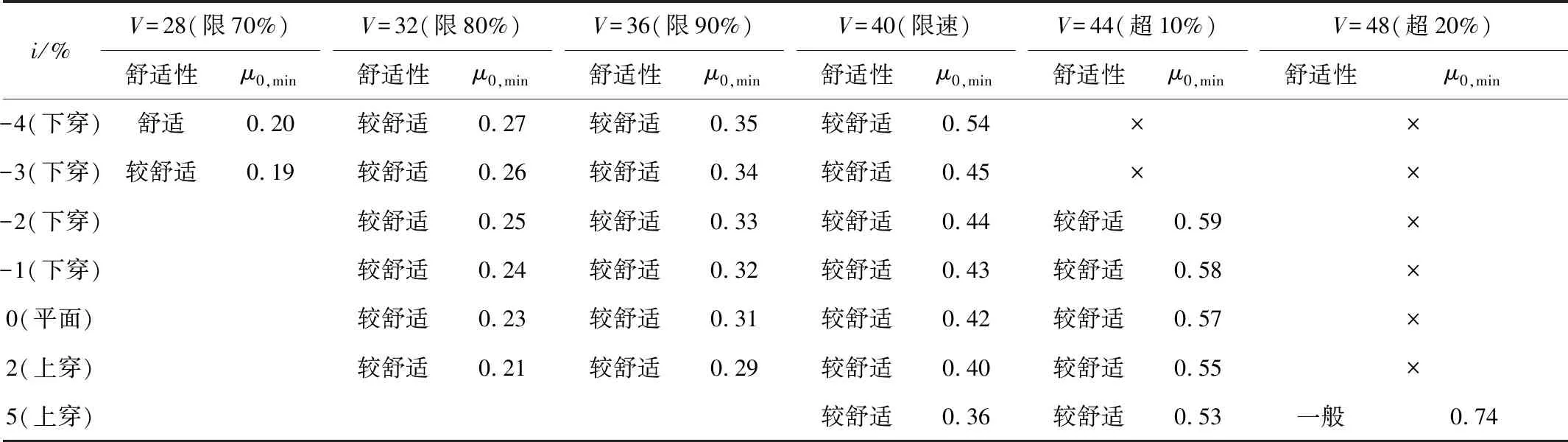
表4 匝道车辆正常行驶时的舒适性及路面最低摩擦系数

4 匝道路面摩擦系数预测公式建立

4.1 路面摩擦系数与车速的关系

不同坡度i的匝道路面摩擦系数μ0与车速V的关系如图4。

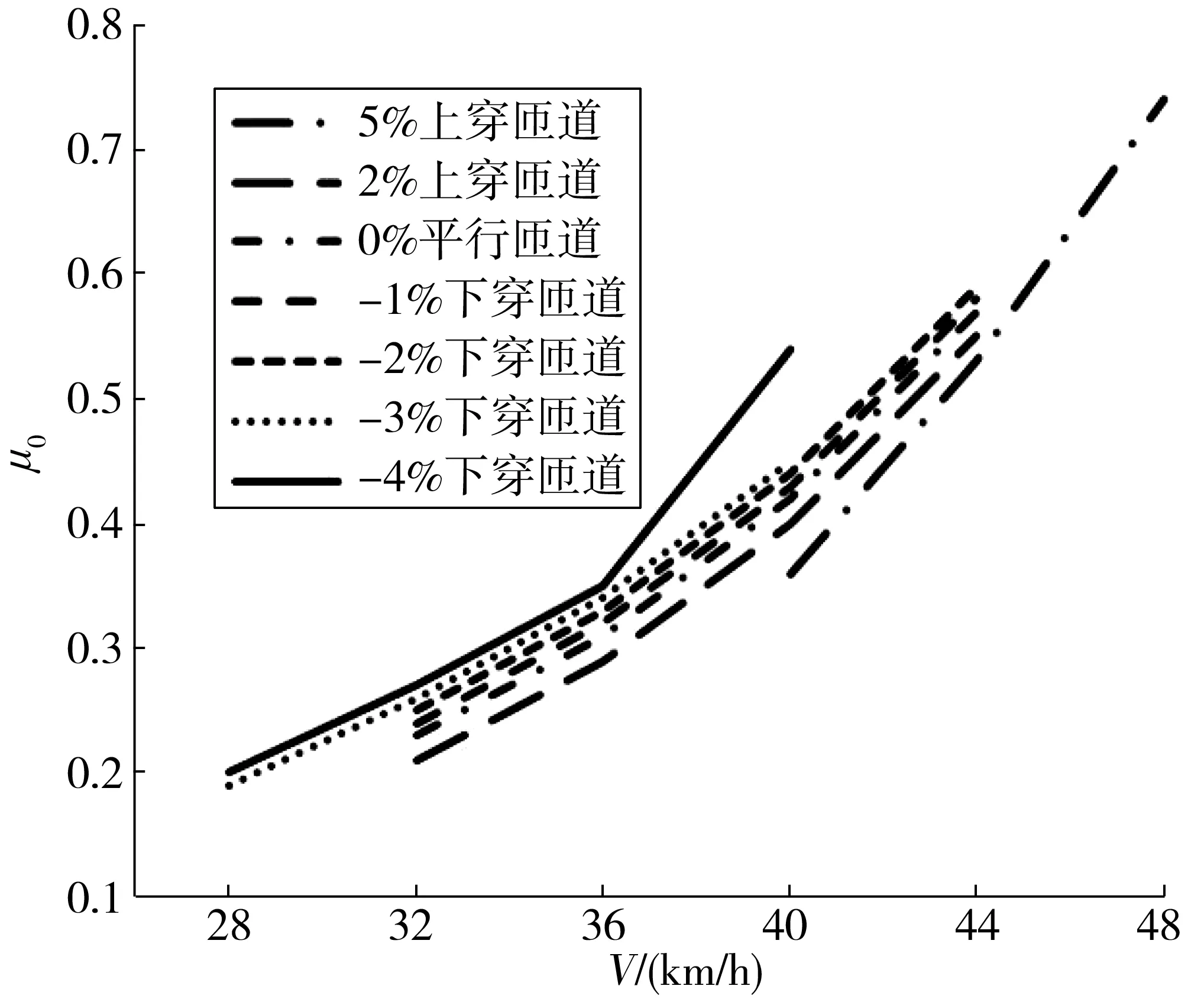
图4 匝道路面摩擦系数μ0与车速V的关系

由图4可见:

1)各种坡度的匝道路面摩擦系数μ0均随车速V的提升而增大,将V控制在44 km/h以下较为安全。

2)当匝道坡度i=5%→-4%时,遵守限速40 km/h的车辆均能保证正常行驶。

3)随着车速的增大,路面摩擦系数呈类似凹型抛物线(斜率逐渐增大)的形式增大,表明车速越大,车辆对路面摩擦系数的要求就越严格。

4.2 匝道路面摩擦系数与匝道坡度的关系

不同车速V下的匝道路面摩擦系数μ0与匝道坡度i的关系如图5。

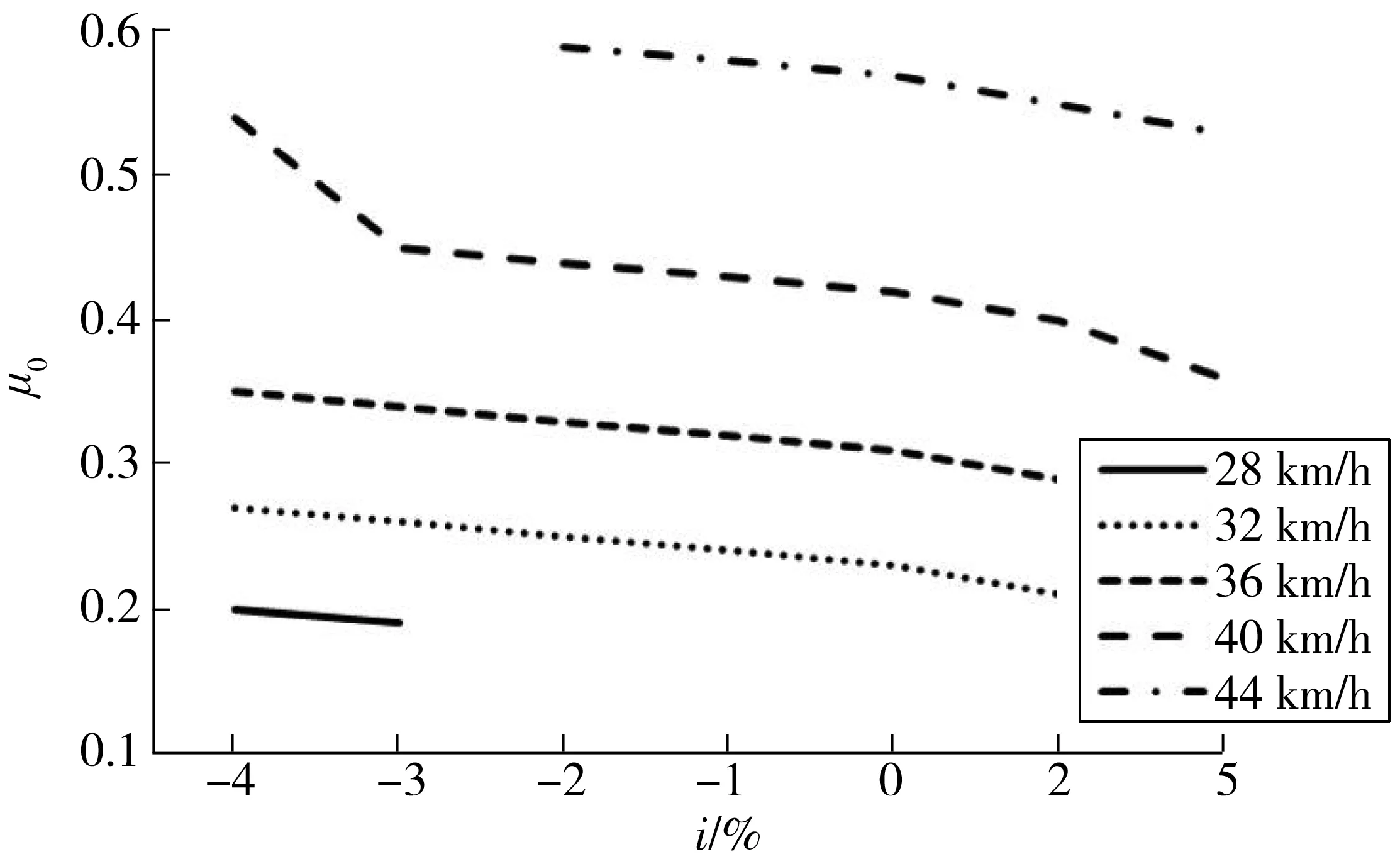
图5 匝道路面摩擦系数μ0与匝道坡度i的关系

由图5可见:

1)各种车速下,匝道路面摩擦系数μ0均随匝道坡度i的增大而减少。

2)随着匝道坡度的改变,匝道路面摩擦系数的变化较为稳定。车速V=28→32→36→40→44 km/h增大时,匝道坡度i每降低1%,匝道路面摩擦系数μ0平均提升0.011、0.011、0.013和0.011。

4.3 基于坡度i的预测公式

由匝道路面摩擦系数μ0与坡度i的关系可知,对于设计速度为40 km/h、半径极限值为50 m的匝道,路面摩擦系数与坡度呈线性关系,因此,笔者进行线性回归。为保证拟合的准确性,当一组数据点不足5个时,不进行拟合。不同车速V的拟合结果如式(2):

(2)

式中:i[-0.04, 0.05]。

4.4 车速-坡度(V-i)二元预测公式

在一元分析的基础上,笔者再进行二元线性回归分析,考虑到摩擦系数随车速的提升具有非线性增长的特点,增加了二元非线性回归分析进行对比。

4.4.1 二元线性回归

二元线性回归参数见表5,回归模型如式(3):

表5 二元线性回归参数

μ0=0.028 5V-1.250 8i-0.697 7,i[-0.04, 0.05]

(3)

由表5可见:回归模型(3)的相关系数R2较大,表示因变量可由自变量解释的程度很高;2个自变量的系数的方差膨胀值FVI均接近1,表示多重共线性较轻;2个自变量系数的显著性均为显著,表示均能够明显影响因变量;回归残差D-W值为0.565 7,显示出较强的自相关性。

此外,在车速很小的时候,由式(3)计算出来的摩擦系数可能为负数,这显然不符合客观规律。分析原因是,公式结构过于简单无法真实反映客观情况,只能计算车速V> 28 km/h的匝道路面摩擦系数。

图6为标准化残差直方图和PP图。可见:残差并未服从正态分布,表示模型预测精度不足;散点与直线有一定偏离,表明样本服从正态分布的效果不佳。

综上,二元线性回归模型(3)可以在一定程度上对匝道路面摩擦系数进行预测,当车速32 km/h≤V≤44 km/h时,准确性较高;但当V在此范围以外时,则无法准确预测。

4.4.2 二元二次非线性回归

在MATLAB中应用Regress函数编写二元二次非线性回归代码,并输出参数和图像。选用的基本二元二次非线性回归公式如式(4):

μ0=b0+b1V2+b2V+b3i2+b4i+b5Vi,

i[-0.04, 0.05]

(4)

为避免设置给定数据中的最小点为最小值时,二元二次非线性回归式出现不符合现实的情况,需要在数据中加上0点。比如在本例中,若回归时将车速28 km/h、匝道坡度-4%设定为最小点,则对于低于28 km/h车速,式(4)计算出来的摩擦系数反而会升高,这不符合现实状况。

回归结果:b0=-0.004 01、b1=0.000 50、b2=-0.009 06、b3=4.902 44、b4=-0.112 28、b5=-0.027 64。

则,式(4)可改写成为式(5):

μ0=-0.004 01 + 0.000 50V2- 0.009 06V+

4.902 44i2-0.112 28i-0.027 64Vi,i[-0.04, 0.05]

(5)

表6为二元二次非线性回归公式(5)的部分参数显著性分析结果。

表6 二元二次非线性回归部分参数显著性分析结果

对比表5及表6,发现二元二次非线性回归的R2比二元线性回归的大,说明二元二次非线性回归更加精确;均方误差EMS=1.222 0 E-4,说明用式(5)可精确描述试验数据。

但是,用二元二次非线性回归限定0点后,在V=10 km/h,i=5%的位置出现了最小值μ0, min=-0.051,不过,该值很小,且现实中匝道不会有如此缓慢的车速,因此可以忽略。总体来看,摩擦系数变化量随车速的提升而增加,而受匝道坡度降低的影响不大。

5 结 论

基于CarSim仿真软件,设计车-路模型、行驶工况和车辆行驶状态评价指标,通过模拟试验对不同车速和坡度的匝道路面抗滑性能进行研究,得到了基于车速-坡度二元因素的匝道路面摩擦系数预测公式,可以较为准确的预测匝道路面摩擦系数。主要结论如下:

1)各种坡度下,匝道路面摩擦系数均随车速的提升而增加,且增幅不断变大。

2)各种车速下,匝道路面摩擦系数均随匝道坡度的增大而减少,但变化幅度较为稳定。

研究内容填补了目前对匝道抗滑性能评价研究的空白,避免以直线路段试验计算得出的摩擦系数在匝道(或小半径弯道)上应用的不准确性,可作为匝道抗滑养护修复的依据或参考。