水平聚类分簇和垂直分组的大规模长序列多比对
2023-10-18王淋,钟诚
王 淋,钟 诚
(广西大学 计算机与电子信息学院,南宁 530004) (广西高校并行分布与智能计算重点实验室,南宁 530004)
1 引 言
序列比对在序列同源性分析、生物序列保守位点识别和系统发育分析等领域具有重要作用[1,2].多序列比对(Multiple Sequence Alignment,MSA)问题是指把两条以上的生物序列进行比对,使相同残基尽可能排在同一列上,以找出这些序列的同源区域[3,4].
从算法设计策略角度,多序列比对方法可以分为树比对、星比对、迭代比对、基于强化学习的比对等.树比对方法先对序列进行层次聚类形成引导树,再从引导树的叶节点自底向上逐步对准序列形成最终的比对结果,代表算法有ClustalW[5]、Kalign[6]、ClustalO[7]和FAMSA[8]等.星比对方法先选取一条中心序列,然后将其他序列分别和中心序列执行对准以形成比对结果,相关算法有MASC[9]和HAlign[10]等.树比对方法和星比对方法都无法纠正序列比对前期的错误,其比对结果质量依赖于比对顺序和中心序列的选取[11].迭代式比对方法通过多次迭代纠正序列比对前期引入的错误,以提升比对的准确率,相关代表算法有MUSCLE[12]、MAFFT[13]、MO-SAStrE[14]、SAPSO[15]和Sequoya[16]等.为进一步提升比对的准确率,Jafari等人研究了将深度强化学习应用于求解多序列比对问题[17].文献[18]提出了一种基于强化学习的序列比对算法RLALIGN.迭代式比对算法运行速度较慢,基于强化学习的比对算法训练时间长且结果难收敛,两者都难以适用于大规模长序列数据集的比对.
第三代测序技术的发展产生了越来越长的序列,这给大规模多序列比对带来了挑战[19].为减少多序列比对算法的运行时间,一种方法是将多序列比对串行算法并行化.针对多序列比对算法常用的并行化技术包括多CPU并行[20,21]、CPU和GPU协同并行[22,23]等.另一种方法是基于划分的思想,将输入序列集拆分比对.算法VDGA将输入序列集中每条长序列垂直分割成多个子序列,分别比对每个子序列,再组合比对结果[24].算法FAME利用求解公共子串的方法直接确定长序列的拆分位置[25],省去了算法VDGA拆分前的比对操作.
为进一步有效比对大规模长序列,本文基于划分思想,提出一种融合水平聚类分簇和垂直分组的多序列比对算法,以在维持较高比对精度的同时,显著加快比对的完成.
2 方 法
设N条长序列的集合S={S0,S1,…,SN-1},序列Si的长度为Li,i=0,1,2,…,N-1.本文提出的融合聚类分簇和垂直分组的大规模长序列比对的思想是:第1阶段,通过融合采用mBed方法和简并字母表方法对S中每条长序列编码,将长序列集S转化为数值短向量集D,利用二分k-means算法聚类D,将S按序列相似度划分为H个水平簇C0,C1,…,CH-1.第2阶段,为每个簇Cj内的长序列集构建最长兼容链,并将簇Cj垂直分割为Vj个包含较短序列的垂直分组Cj,0,Cj,1,…,Cj,Vj-1,j=0,1,2,…,H-1.第3阶段,对簇Cj中的每个垂直分组Cj,p,若其是非最长兼容链选中的垂直分组,则使用已有的适用于规模较小的多序列比对算法对准Cj,p中的序列,以得到簇Cj的完整比对结果,j=0,1,2,…,H-1,p=0,1,2,…,Vj-1.第4阶段,构建水平簇集{C0,C1,…,CH-1}的最长兼容链,将序列集S划分为NG个簇间分组CG0,CG1,CG2,…,CGNG-1,利用本文提出的带有Gap类型推断的动态规划渐进比对方法分别对准每个非最长兼容链选中的簇间分组,以获得最终的N条长序列的比对结果.
下面详细阐述融合水平聚类分簇和垂直分组策略对N条长序列进行比对的方法.
2.1 多序列聚类分簇
聚类分簇是指对长序列集S进行聚类,按序列相似度将S划分成H个水平簇C0,C1,…,CH-1,使得簇Cj中各条序列尽可能相似,j=0,1,2,…,H-1.聚类分簇使得簇内序列拥有更多公共子片段且大部分公共子片段在垂直分组过程中直接对准,这将极大地降低第3阶段需要比对的数据规模.聚类分簇工作首先对S中每条长序列编码,将长序列集S转化为数值短向量集D,然后通过对D进行聚类,将长序列集S分簇,同时生成引导树GT用于簇合并.
为降低数值向量的维数,以加速大规模长序列的聚类,首先采用mBed方法[26]从序列集S中选取m条序列记为M0,M1,…,Mm-1;其次,采用简并字母表方法[27]分别计算序列S0,S1,…,SN-1的k-mer编码向量;然后,计算Si与Mj对应的k-mer编码向量的欧氏空间距离D(Si,Mj),j=0,1,2,…,m-1,i=0,1,2,…,N-1,m=(log2N)2.最后,将(D(Si,M0),D(Si,M1),…,D(Si,Mm-1))作为Si对应的数值向量Di,i=0,1,2,…N-1.将S中每条序列编码得到数值短向量集D.通过二分k-means算法[28]对D进行聚类,以实现序列集S的水平划分.
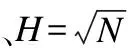
算法1.MS-kCluster
输入:长序列数据集S={S0,S1,…,SN-1}
输出:划分S后的H个水平簇C0,C1,…,CH-1的集合Clusters、引导树GT
Begin:
1.采用mBed方法从长序列集S中选取m=(log2N)2条长序列,记为M0,M1,…,Mm-1;
2.fori=0toN-1do
3. 通过简并字母表方法计算长序列Si的k-mer编码向量KV(Si);
4.endfor
5.fori=0toN-1do
6.forj=0tom-1do
7. 计算KV(Si)与KV(Mj)的欧氏空间距离D(Si,Mj);
8.endfor
9. 计算Si对应的数值向量Di=(D(Si,M0),D(Si,M1),…,D(Si,Mm-1));
10.endfor
11.node←Node(D);//Node(D)表示初始化引导树GT的新节点,并将数值向量集合D作为新节点的值
12.初始化引导树GT←node且树当前叶节点的集合CS←{node};
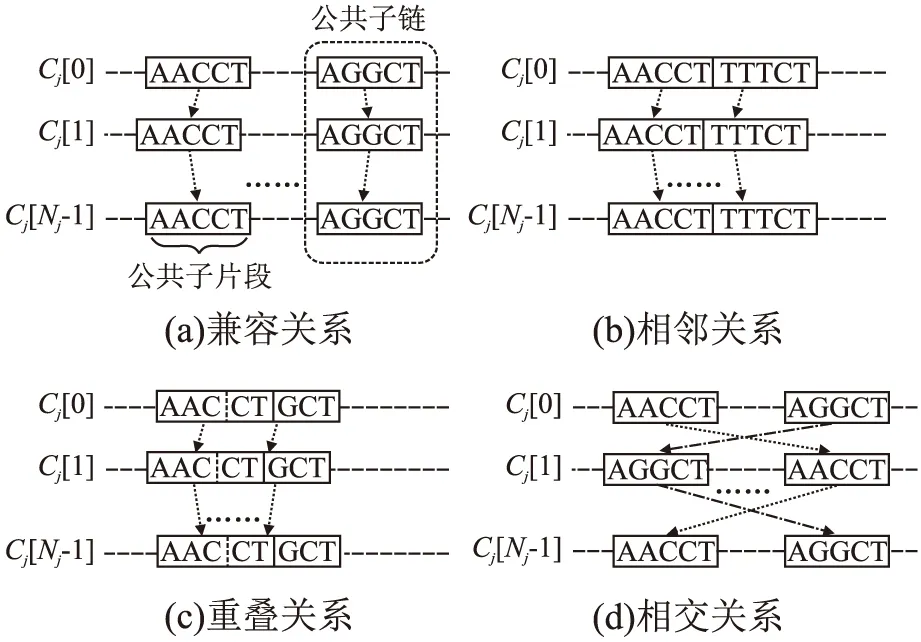
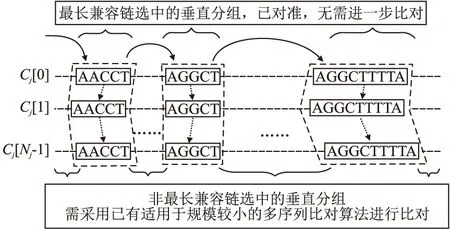
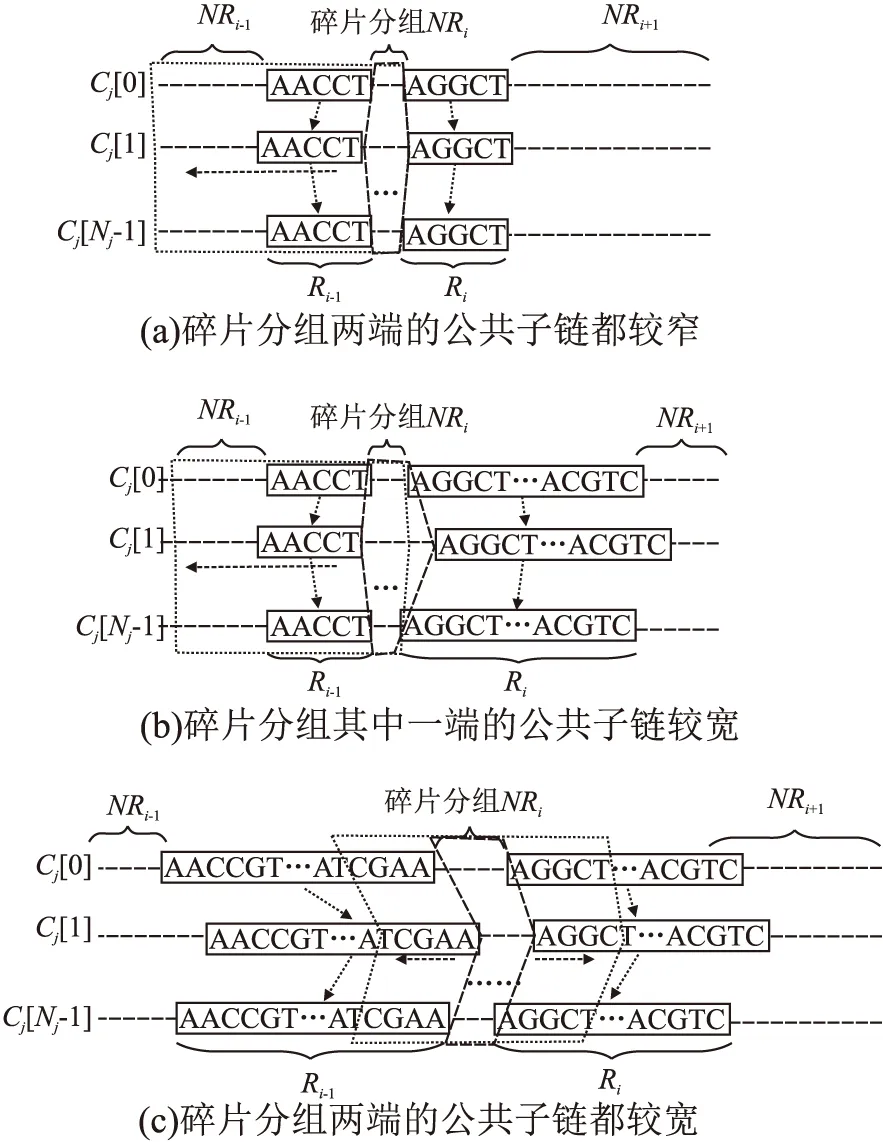
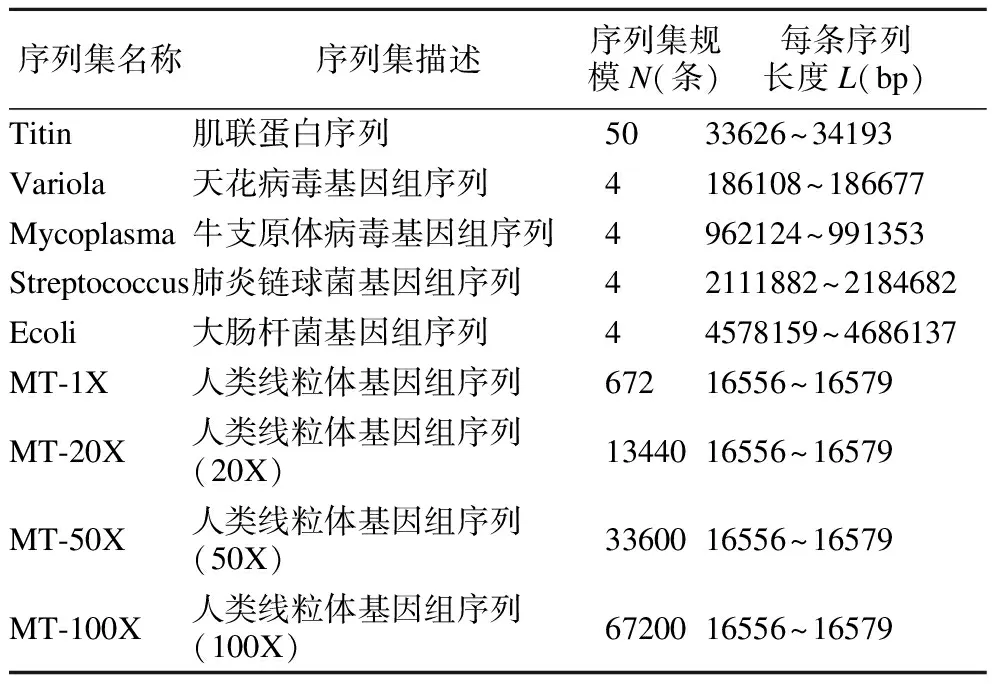
13.while(CS中节点数量 14.node←CS中具有最大SSE值的节点; 15. 使用k-means聚类算法将节点node中包含的数值向量集合分割为两个子集合Dleft、Dright; 16.node.left←Node(Dleft);//node.left表示引导树节点node的左子节点 17.node.right←Node(Dright);//node.right表示引导树节点node的右子节点 18. 删除CS集中的node节点,并将node.left和node.right加入到CS集; 19.endwhile 20.Clusters←{}; 21.fornodeinCSdo 22.Clusters←Clusters∪{节点node中数值向量集对应的序列集合}; 23.endfor End 经聚类分簇后,长序列集S被划分为H个簇C0,C1,…,CH-1.每个簇内序列数量大幅减少,但簇内序列的长度没有改变,若直接采用现有的多序列比对算法对簇内的长序列进行比对,算法仍需要较高的计算开销.为降低大规模长序列比对的时间,需在序列长度维度上对簇内序列进一步进行垂直划分.为提高垂直划分的准确性,以提升后续比对精度的同时降低后续比对的时间,本文在FAME算法[25]的基础上,改进了最长兼容链构建算法以选择具有最大加权长度和的公共子链集合,并在簇内序列垂直分割时引入碎片分组扩展,进而设计簇内序列垂直分组方法分别对每个簇Cj进行划分,j=0,1,2,…,H-1.本文给出的簇内序列垂直分组方法包括寻找公共子片段、生成公共子链、构建最长兼容链和簇内序列垂直分割4个步骤. 2.2.1 寻找公共子片段 寻找公共子片段的目的是找到簇内序列的潜在切割点.设簇Cj中包含的长序列数量为Nj,Cj[u]表示簇Cj中的第u条序列,u=0,1,2,…,Nj-1,j=0,1,2,…,H-1.若有v个k-mer在簇Cj的每条序列中均出现,则这些k-mer被称为公共k-mer,记为km0,km1,…,kmv-1,公共k-mer的长度k=「log2L⎤,L为簇中序列的平均长度[25].令Npos(Cj[u],kmi)表示kmi在序列Cj[u]中出现的次数,本文采用kmi在簇Cj中的冗余度Redundancy(Cj,kmi)[25]和冗余度阈值Threshold(Cj,kmi)[25]来确定簇Cj中长序列的公共子片段.冗余度Redundancy(Cj,kmi)和冗余度阈值Threshold的计算分别如式(1)和式(2)所示[25]: (1) (2) 簇Cj中序列公共子片段为冗余度小于阈值Thresholdj的公共k-mer.公共k-mer确定了簇内序列垂直分割的潜在切割点,但冗余度过大的公共k-mer在簇内各序列中频繁出现,会导致垂直分割精度下降的同时也加大了计算开销.为此,通过冗余度阈值过滤掉冗余度较大的那些公共k-mer.本文寻找簇Cj的公共子片段的过程如下: 第1步.寻找簇Cj中最短序列的下标idxmin. 第2步.采用滑动窗口策略提取序列Cj[idxmin]中的k-mer,将k-mer及其在序列Cj[idxmin]中出现的次数作为键值对,存入Hash表Hres. 第3步.u←0. 第4步.若u=idxmin,则转至第6步;否则通过滑动窗口提取序列Cj[u]中的k-mer,若Hres[k-mer]存在,则将此k-mer及其在序列Cj[u]中出现的次数存入Hash表Hu,并标记Hres[k-mer]. 第5步.遍历Hash表Hres,对于Hres中的每个k-mer,若其已被标记,则执行Hres[k-mer]←Hres[k-mer] *Hu[k-mer];否则从Hres中删除此k-mer. 第6步.u←u+1,重复第4~第6步,直至u=Nj为止. 第7步.遍历Hres,对于Hres中每个k-mer,若Hres[k-mer] >Thresholdj,则从Hres中删除此k-mer. 第8步.提取Hres中的k-mer作为簇Cj的公共子片段. 2.2.2 生成公共子链 确定公共子片段之后,通过将簇中不同序列的相同公共子片段进行组合,以生成公共子链.簇Cj的公共子链的数目等于簇中各公共子片段的冗余度Thresholdj之和,j=0,1,2,…,H-1. 根据公共子链的位置关系,本文将公共子链分为兼容关系、相邻关系、重叠关系和交叉关系.图1给出了序列公共子链位置关系的示例. 图1 序列公共子链位置关系示例Fig.1 Example for positional relationship of common subchains in sequences 从图1可知,相邻关系(b)和重叠关系(c)的公共子链之间无间隙Gap且合并时无冲突,可将其合并以降低最长兼容链构建的时间开销.合并具有相邻关系和重叠关系的公共子链后,剩余的公共子链还可能存在兼容关系(a)和相交关系(d).若公共子链之间存在相交关系,则无法根据公共子链对簇内序列进行垂直分割.为此,本文通过构建最长兼容链,选择公共子链集合的一个兼容子集,以去除具有相交关系的公共子链. 2.2.3 构建最长兼容链 兼容链是公共子链按照位置排序串成的一条链,在这条链中,任意两个公共子链均满足兼容关系[25].最长兼容链是具有最多公共子链的兼容链[25].这个最长兼容链的定义将所有公共子链平等看待,忽视了公共子链宽度对后续分割精度的影响. 为提高垂直分割的精度,以提升后续比对的精度和降低比对的时间,本文根据公共子链宽度对公共子链进行加权,设计一个新的算法以选择具有最大公共子链加权长度和的兼容链作为最长兼容链.令K表示公共子链的数量,LST表示长度为K的列表,LST中每个元素都保存如下信息:公共子链subchain,subchain所在兼容链的权值weight,subchain所在兼容链的前驱节点在LST中的下标previous.算法2描述本文提出的构建最长兼容链的算法Build-LCC. 算法2.Build-LCC 输入:含有兼容关系和相交关系的公共子链列表subchains 输出:最长兼容链LCC Begin: 1.按前后位置关系对列表subchains中的公共子链进行排序; 2.LST←φ; 3.forchaininsubchainsdo 4.weight←公共子链chain的宽度; 5. 倒序遍历LST,找到第i个位置,使得LST[i].chain与chain是兼容关系;若没有找到,则i←-1; 6.previous←i; 7.if(i≠-1)then 8.weight←weight+LST[i].weight; 9.endif 10. 从第i个位置开始正向遍历LST,找到第j个位置,使得LST[j].weight>weight;若没有找到,则j←Length(LST);//Length(LST)为LST的长度; 11. 将{chain,weight,previous}插入到列表LST的第j个位置; 12.endfor 13.初始化链表LCC节点存储公共子链chain; 14.pos←Length(LST)- 1; 15.while(pos≠-1)do 16. 将LST[pos].chain插入到链表LCC的头部; 17.pos←LST[pos].previous; 18.endwhile End 算法Build-LCC步骤1需时间O(K×log2K),步骤2~步骤12最坏情形下需时间O(K2),步骤13~步骤18最坏情形下需时间O(K).因此,算法Build-LCC的时间复杂度为O(K2).LST列表所需空间开销为O(K),链表LCC所需空间开销为O(K).因此,算法Build-LCC的空间复杂度为O(K). 2.2.4 簇内序列垂直分割 最长兼容链构建后,其公共子链间仅存在兼容关系,可根据链中的公共子链对簇Cj中的序列进行垂直分割,将簇Cj划分为多个垂直分组.图2给出垂直分割簇Cj的示例. 图2 垂直分割簇Cj示例Fig.2 Example of splitting cluster Cj vertically 图2中,簇Cj划分后的垂直分组分为最长兼容链选中的垂直分组和非最长兼容链选中的垂直分组.最长兼容链选中的垂直分组即公共子链,其内的各序列片段已对准,无需进一步比对.对于非最长兼容链选中的垂直分组,需使用已有的适用于规模较小的多序列比对算法进行多序列比对. 对于非最长兼容链选中的垂直分组,若分组内的序列片段太短,则无法为后续使用的多序列比对算法提供足够的残基信息,这可能导致比对精度下降.本文将此类含有较短序列的非最长兼容链选中的垂直分组称为碎片分组.本文通过对碎片分组进行扩展,以提升后续比对的精度. 设最长兼容链中包含的公共子链数量为Length(LCC),Ri表示第i个最长兼容链选中的垂直分组,NRj表示第j个非最长兼容链选中的垂直分组,Length(Ri)表示Ri中的序列长度,Length(NRi)表示NRi中序列的平均长度,0≤i≤Length(LCC)-1,0≤j≤Length(LCC).设NRi是碎片分组,图3给出扩展碎片分组NRi的示例. 图3 对碎片分组NRi扩展的示例Fig.3 Example of extending fragmented partition NRi 对于碎片分组NRi两端的公共子链都较窄(图3(a))的情形,若Length(NRi-1) 经簇内序列垂直分割和碎片分组扩展后,簇Cj被划分为Vj个垂直分组Cj,0,Cj,1,…,Cj,Vj-1,j=0,1,2,…,H-1,兼容链选中的垂直分组内的序列已对准,无需后续比对,但非最长兼容链选中的垂直分组内的序列仍未对准,需进一步使用已有的适用于规模较小的多序列比对算法将其对准. 若簇Cj中的垂直分组Cj,p为非最长兼容链选中的垂直分组,则使用已有的适用于规模较小的多序列比对算法对此垂直分组内的序列进行对准,并将比对结果中的Gap写入簇Cj内序列的相应位置.将簇Cj划分得到的每个非最长兼容链选中的垂直分组均对准后,得到簇Cj内多条长序列的完整比对结果,p=0,1,2,…,Vj-1,j=0,1,2,…,H-1. 簇Cj经过簇内序列垂直分组与簇内分组对准后,簇Cj内的那些序列已对准,j=0,1,2,…,H-1,但簇与簇之间的序列尚未对准.为得到序列集S的完整比对结果,还需进行簇间序列水平合并,即以簇为单位将簇C0,C1,…,CH-1进行对准. 2.4.1 簇间序列垂直分组 由于对准过程中添加的间隙Gap的影响,簇Cj的长度LCj大于等于簇Cj中原始序列的最大长度,j=0,1,2,…,H-1.对于大规模长序列集S,若直接通过比对算法比对各簇,则计算开销仍然相当大.为此,设计簇间序列垂直分组方法,通过寻找簇间公共子片段构成的最长兼容链,将簇Cj垂直划分为NG组,得到{Gj,0,Gj,1,…,Gj,NG-1},j=0,1,2,…,H-1,记各簇中的第k组序列组成的集合为簇间分组CGk={G0,k,G1,k,…,GH-1,k},k=0,1,2,…,NG-1,对划分得到的各个簇间分组分别进行对准,以减少簇合并的时间开销. 为进行簇间序列垂直分组,首先将簇Cj映射表示为相同长度LCj的序列Sj,j=0,1,2,…,H-1.对于簇Cj中的每一列,都用序列Sj中的一个字符表示,Sj中第i个字符表示簇Cj中的第i列,若簇Cj第i列中的每个字符都相同,则用簇Cj第i列的字符代替序列Sj中第i个字符,否则用符号‘?’代替序列Sj中的第i个字符,i=0,1,2,…,LCj-1. 获得簇C0,C1,…,CH-1的代表序列S0,S1,…,SH-1之后,对序列S0,S1,…,SH-1依次进行寻找公共子片段、生成公共子链、构建最长兼容链和序列垂直分割.与簇内序列垂直分组不同的是,在寻找公共子片段中提取每条序列的k-mer时,需剔除含有符号‘?’的k-mer;在簇间序列垂直切割中划分Sj时,需在簇Cj的相同列上也进行划分,j=0,1,2,…,H-1. 经过簇间序列垂直分组,簇Cj被垂直划分为NG组Gj,0,Gj,1,…,Gj,NG-1,j=0,1,2,…,H-1,将各簇中第k组进行组合得到簇间分组CGk={G0,k,,G1,k,…,GH-1,k},k=0,1,2,…,NG-1. 划分后的簇间分组包括最长兼容链选中的簇间分组和非最长兼容链选中的簇间分组两类,对于最长兼容链选中的簇间分组,其内的序列已对准,无需进一步比对;对于非最长兼容链选中的簇间分组,需做进一步对准. 2.4.2 簇间分组对准 簇间垂直分组之后,得到簇间分组CG0,CG1,…,CGNG-1,需依次对准每个非最长兼容链选中的簇间分组以获得序列集S的完整比对结果. 为提升簇间分组CGk={G0,k,,G1,k,…,GH-1,k}比对结果的准确度,k=0,1,2,…,NG-1,本文设计一种新的带有间隙Gap类型推断的动态规划渐进比对方法. 本文使用基于仿射变换罚分的动态规划渐进比对方法对准分组Gi,k和Gj,k,0 ≤i,j 计算比对路径的得分即对准结果SGi,j的比对得分AlignScore(i,j)[11],如式(3)所示: AlignScore(i,j)= (3) 式(3)中,LSG为对准结果SGi,j的列数,NGi、NGj分别表示分组Gi,k和Gj,k中包含的序列数量,β(Gi,k,b,a)表示对准后组Gi,k中第b条序列的第a个字符(包括Gap),s(c1,c2)表示字符c1与字符c2的替换分数,s(c1,c2)由间隙Gap罚分方法及DNA/RNA或蛋白质替换计分矩阵共同确定. 仿射变换罚分方法将间隙Gap分为4类:开放Gap、扩展Gap、终端开放Gap和终端扩展Gap,不同Gap类型具有不同的罚分,即不同的s(c1,c2)值[29].现有的多序列比对算法在利用动态规划方法计算AlignScore(i,j)时,大多不考虑序列分组中已有的Gap与新插入Gap之间类型的相互影响,这导致计算的比对得分有所偏差. 本文在仿射变换罚分的动态规划渐进比对方法基础上,通过在比对过程中引入Gap类型推断计算出准确的比对得分,以提高分组Gi,k和Gj,k对准的精度.为进行Gap类型推断,需在比对时获取各Gap在分组内序列中的位置信息、上一比对状态信息、当前比对状态信息和下一比对状态信息. 为在比对时快速获得Gap的位置信息,首先根据Gap在组内序列中的位置,将Gap细分为8类.图4给出根据Gap在组内序列中的位置对Gap进行分类的示例. 图4 在组内序列中的位置对Gap进行分类的示例Fig.4 Example of classifying Gap based on its position in the sequence in group 接着将分组Gi,k转换为采用规模为(ξalpha+ξgap)×LGi的二维矩阵Pi表示,其中ξalpha表示生物序列字符表的大小(对于DNA或RNA序列ξalpha=4,对于蛋白质序列ξalpha=20),ξgap=8表示Gap种类数为8,矩阵Pi的第m列中,前ξalpha行元素表示组Gi,k第m列中不同字符出现的频数,后ξgap行元素表示不同Gap类型在组Gi,k第m列中出现的次数.然后,按相同方法将组Gj,k转换为采用规模为(ξalpha+ξgap)×LGj的二维矩阵Pj表示.以Pi、Pj分别替代分组Gi,k和Gj,k作为动态规划比对方法的输入. 根据动态规划矩阵Pi及其当前比对列编号a、Pj及其当前比对列编号b、上一比对状态信息、当前比对状态信息和下一比对状态信息,即可推断出当前比对状态对应列的Gap的详细信息.图5给出进行Gap类型推断的示例. 在图5中,若上一比对状态为X,当前比对状态为M,下一比对状态为Y,则仅根据矩阵Pi第a列可得矩阵Pi第a列Gap类型推断的结果,仅根据矩阵Pj第b列可得矩阵Pj第b列Gap类型推断的结果.图5中箭头表示推断后各类Gap的数量与原始Gap数量之间的关系. 图5 比对过程中进行Gap类型推断的示例Fig.5 Example of Gap inference during alignment 由Gap类型推断的结果,根据相应的罚分参数和替换计分矩阵可得当前比对状态的得分,将比对路径中各状态节点的得分相加即为比对路径的得分.通过带有间隙Gap类型推断的动态规划渐进比对方法寻找得分最高的比对路径,并执行路径上各状态节点对应的操作即得分组Gi,k和Gj,k的对准结果SGi,j. 沿水平聚类分簇得到的引导树GT,自底向上利用带有间隙Gap类型推断的动态规划渐进比对方法对准CGk内的两两分组后,即得到CGk的比对结果,k=0,1,2,…,NG-1. 对每个簇间分组CG0,CG1,CG2,…,CGNG-1依次进行簇间分组对准后,即可得到序列集S的完整比对结果. 为方便理解,图6给出了本文提出的面向大规模长序列的多比对算法的处理流程. 图6 大规模长序列多比对流程Fig.6 Procedure of multiple alignment for large-scale long reads 算法3描述了本文提出的融合聚类分簇和垂直分组的大规模长序列多比对算法(简称GridMSA算法). 算法3.GridMSA 输入:长序列集S={S0,S1,…,SN-1} 输出:带有Gap的多序列比对结果S Begin: 1.fori=0toN-1do 2. 运用mBed方法及简并字母表方法将长序列Si编码为长度为(log2N)2的数值向量Di; 3.endfor 4.通过二分k-means算法聚类数值向量D0,D1,…,DN-1,获得引导树GT及序列集S的聚类结果,将S按序列相似度划分为H簇C0,C1,…CH-1; 5.forj=0toH-1do 6. 通过簇内垂直分组算法寻找簇Cj中以序列公共子片段构成的最长兼容链,将簇Cj垂直分割为Vj组Cj,0,Cj,1,…,Cj,vj-1; 7.fork=0toVj-1do 8. 若Cj,k为非最长兼容链选中的垂直分组,则执行现有的适用于规模较小的多序列比对算法对准Cj,k内序列,并将比对结果中的Gap添加到S中原序列的对应位置,以获得簇Cj内各序列的比对结果; 9.endfor 10.endfor 11.通过簇间序列垂直分组算法寻找簇C0,C1,…CH-1之间公共子片段构成的最长兼容链,将序列集S划分为NG个簇间分组CG0,CG1,…,CGNG-1; 12.fork=0toNG-1do 13. 若CGk为非最长兼容链选中的簇间分组,则执行动态规划渐进比对方法对准簇间分组CGk内的各组G0,k,G1,k,…GH-1,k,并将比对结果中的Gap添加到S中原序列的对应位置; 14.endfor End 1http://github.com/naznoosh/msa 实验在广西大学Sugon 7000A超级并行计算机系统进行.使用节点的处理器为Intel Xeon Gold 6230,CPU主频2.1GHz,动态加速频率3.9GHz,节点的DDR4内存频率为2933MHz,内存容量512GB,硬盘容量8×900GB.运行64位CentOS 7.4操作系统.采用C语言编程实现算法. 表1 实验使用的长序列数据集信息Table 1 Information of experimental long-read datasets used 本文同样采用文献[25]使用的数据集进行实验,该数据集可从Github网站1免费获得.数据集中包含9个不同的长序列集,各序列集的信息如表1所示.注:Github网站上未提供文献[25]提到的超长序列集Sorangium cellulosum,因此表1中没有包含此数据集. 实验测试了本文算法GridMSA和同类算法MAFFT[13]、ClustalO[7]、ClustalW[5]、FAMSA[8]、FAME[25]在不同序列集上运行的比对结果质量(SPavg)[25]和时间(Time). 设序列集S对准后每条序列的长度为L,Si,j表示比对完成后S中第i条序列的第j个字符,0≤i (4) 本文算法GridMSA在水平聚类分簇时通过k-mer编码将字符序列转换为数值向量,以计算序列间的距离,参照文献[28]选取k1=5对DNA序列和RNA序列进行编码、选取k1=2对蛋白质序列进行编码.算法GridMSA在垂直分组时需依据k-mer寻找长序列的公共子片段,为此参照文献[25]设置k2=「log2Lavg⎤,Lavg为S中序列的平均长度.本文使用与文献[28]相同的替换计分矩阵.为设置空隙Gap罚分参数,将本文8种不同Gap类型映射到文献[28]中4种不同Gap类型,对应关系如表2所示. 表2 Gap类型映射及罚分取值Table 2 Gap type mapping and penalty setting 本文将实现多序列比对算法FAME时分别执行适用于规模较小的多序列比对算法MAFFT、ClustalO、ClustalW、FAMSA完成对垂直分组得到各分组中的序列进行比对的版本分别记为FAME1、FAME2、FAME3和FAME4.同时,将实现多序列比对算法GridMSA时分别执行适用于规模较小的多序列比对算法MAFFT、ClustalO、ClustalW、FAMSA完成对垂直分组得到各分组中的序列进行比对的版本分别记为GridMSA1、GridMSA2、GridMSA3和GridMSA4. 实验首先测试了算法在大规模长序列数据集Titin、Variola、Mycoplasma、Streptococcus和Ecoli上的运行时间(Time)和比对结果质量(SPavg),结果如表3所示. 根据表3的实验结果,在长序列数据集Titin、Variola、Mycoplasma、Streptococcus和Ecoli上,本文算法实验结果得到的SPavg值大部分比其他同类算法实验得到的SPavg值更接近0,这表明本文算法GridMSA实现的4个版本GridMSA1、GridMSA2、GridMSA3和GridMSA4在进行比对时均具有整体上较好的比对结果质量和较低的运行时间开销,其中在超长序列集Streptococcus和Ecoli上运行的效果优势更为明显.这主要是因为算法GridMSA在垂直分组时选择具有最大公共子链长度和的兼容链作为最长兼容链,一方面使得划分后的待比对区域长度减小,从而降低了比对时间,另一方面最长兼容链选择区域更加合理,从而提升了比对精度;此外算法GridMSA将垂直分割后的碎片分组扩展,为后续多序列比对提供了足够的残基信息,这进一步提升了比对精度. 为评估算法在不同规模的同一个数据集上运行的比对效果,实验进一步测试了算法在数据集MT-1X、MT-20X、MT-50X、MT-100X上的运行时间(Time)和比对结果质量(SPavg),结果如表4所示. 从表4的实验结果可以看到:在大规模长序列数据集MT-1X~MT-100X上,与其他算法相比,本文算法GridMSA实现的4个版本GridMSA1、GridMSA2、GridMSA3和GridMSA4进行多序列比对在整体上保持比对精度的同时,所需的时间开销更少.当序列集数据规模越大时,与其他算法相比,本文算法GridMSA进行多序列比对获得的加速效果越为明显.这主要是因为算法GridMSA通过融合水平聚类分簇和垂直分组,将原始大规模长序列比对问题分解为若干比对子问题进行求解,从而降低了比对时间;同时算法GridMSA在簇间分组对准时考虑到簇中已有Gap与新插入Gap之间类型的相互影响,在动态规划渐进比对过程中引入Gap类型推断计算出了准确的比对得分,从而确保了比对的精度.虽然算法FAME在大规模序列数据集上运行也具有较好的比对结果质量和较低的时间开销,但由于算法FAME仅对序列集进行垂直分割,划分后各子序列集的序列数量并没有减少,它对垂直分割得到的各子序列集中的序列进行多比对较为耗时,所以其所需的比对时间高于本文算法GridMSA. 表3 算法在5种长序列集上运行的时间和比对结果质量Table 3 Required time and values of SPavg of running the algorithms on five long-read sets 综合表3和表4的实验结果可知:采用本文算法GridMSA对大规模长序列数据集进行多比对,整体上可以大大降低比对时间且获得较好的比对结果质量.序列集规模越大、序列长度越长,算法GridMSA加速效果优势越为明显.算法GridMSA在垂直分组时选择具有最大公共子链长度和的兼容链作为最长兼容链并对垂直分割后的碎片分组进行扩展,同时在簇间序列水平合并过程中引入间隙Gap类型推断计算出准确的对准得分,因此算法GridMSA对大规模的长序列集进行多比对,仍可以获得较高的比对结果质量得分.另一方面,在9组数据集上的实验结果表明,当长序列集数据规模相对较小时,算法GridMSA执行适用于规模较小的多比对算法MAFFT对垂直分组得到各分组中的序列进行比对时,获得整体上较好的多序列比对结果;当长序列集数据规模较大时,算法GridMSA执行适用于规模较小的多比对算法FAMSA对垂直分组得到各分组中的序列进行比对时,获得整体上较好的多序列比对结果. 本文的研究特色和新颖点是:基于划分思想,通过融合水平聚类分簇和垂直分组将大规模长序列集划分成多个规模相对较小、长度较短的子序列集;通过在构建最长兼容链时对公共子链按其宽度加权、在簇内序列垂直分割时进行碎片分组扩展,进而设计了簇内序列垂直分组方法,利用此方法垂直分割水平簇以提升后续比对的质量和速度;提出针对水平簇集的簇间序列分组算法,在簇间序列水平合并时利用簇间序列分组算法将大规模长序列数据集垂直划分为多个簇间分组分别进行比对,以加快比对速度;利用水平簇内序列多比对结果中包含的Gap信息,设计了一种新的带有Gap类型推断的动态规划渐进比对方法,利用此方法对划分得到的各簇间分组分别进行多比对,可以确保大规模长序列比对结果保持较高的精度.在大规模长序列数据集上的实验结果表明,本文算法GridMSA在整体上维持较高的多比对结果质量的同时,大大地减少了大规模长序列多比对的计算时间;当数据规模越大、序列长度越长的时候,本文算法加速效果越明显.本文算法GridMSA的运行时间和待比对的序列长度以及数据规模成正相关,当数据集规模更大、序列更长的时候,算法GridMSA仍需要较长的时间开销.如何通过CPU+GPU协同并行计算加速算法GridMSA以适应更长序列更大规模的多序列比对问题将是下一步研究方向.2.2 簇内序列垂直分组
2.3 对准簇内分组
2.4 簇间序列水平合并


2.5 比对算法

3 实 验
3.1 实验环境与数据
3.2 结果实验
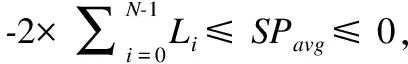


4 总 结
