具有双参数发展系统的随机脉冲随机集值微分系统的可控性
2023-10-17李文胜
李文胜
(西安航空学院 理学院,西安 710077)
0 引言
微分包含作为微分方程和不等式的一种推广,具有非常重要的意义。近几十年来,微分包含有关理论得到了广泛关注。Li等[1]探讨了一类时滞依赖于状态的脉冲中立型发展微分包含解的存在性
式中,A(t)是在Banach空间上定义的线性闭算子族,其产生双参数发展系统U(t,s)。假设U(t,s)是紧且有界的,g是连续的,F是可测的,Li等[1]先将所给模型转化成对应的积分方程,然后应用微分包含理论、双参数发展系统结合凝聚映射不动点定理,在公理化的抽象的象空间B上证明了此类方程温和解的存在性。
Malinowski和Michta[2]研究了随机微分包含和集值微分方程之间的关系


F1和G1是非激励集值随机过程,作者利用微分包含结合随机过程有关理论,在给定条件的基础上,证明了所给方程解的存在性。文中集值微分方程的解是定义在由L×L随机向量空间的非空、有界、闭凸子集构成的超空间。在此基础上,证明了随机微分包含对应的集值随机微分方程的解,该结果能够推断出随机微分包含问题的可解集,同时考虑随机微分包含问题解的存在性。
Debbouche和Antonov[3]引入了脉冲控制包含条件的概念,即首次将脉冲条件作为多值映射和控制的包含条件。建立了巴拿赫空间中一类半线性Hilfer分数阶微分控制包含的近似可控性概念。对于主要结果,Debbouche和Antonov[3]使用了不动点定理、集值映射结合算子半群理论,研究了对应的一类半线性Hilfer分数阶微分包含的近似可控性。
Ahmad和Luca[4]讨论了一类非局部边界条件下序列分数阶积分-微分方程及包含解的存在性。作者考虑了涉及黎曼-刘维尔积分和黎曼-斯蒂尔杰斯积分的Caputo型序列分数阶积分微分方程和包含在非局部边界条件下解的存在性。利用收缩映射原理和Krasnoselskii不动点定理来证明分数阶方程中的两个算子之和,以及非线性替代的Leray-Schauder类型来证明Kakutani映射,以及Covitz-Nadler不动点定理来证明分数阶包含。最后,给出了一些例子来说明主要结果。
Ravichandran等[5]利用Krasnoselskii不动点定理和Leray-Schauder定理结合预解析算子和一些解析方法研究了一类巴纳赫空间中时滞依赖状态的分数阶中立型积分微分系统精确能控性的新结果,并提供了一个应用程序来举例说明这个概念。
Dineshkumar等[6]主要研究了Sobolev型分数阶随机积分-微分时滞包含的近似能控性。利用分数阶微积分、多值映射、Bohnenblast和Karlin不动点定理的结果证明论文主要结果。首先,作者研究了模型的近似能控性,然后进一步讨论了非局部条件的对应模型。最后,给出了一个应用实例来说明所得到的理论结果。文献[7-12]从不同的角度对微分包含进行了研究。
本文在上述工作基础上,研究了一类双参数发展系统下具有时滞依赖状态的随机脉冲随机集值微分方程
(1)
x0=φ
(2)
x(ξk)=bk(τk)x(ξk),i=1,2,…,n
(3)
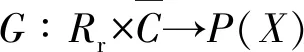
1 预备知识

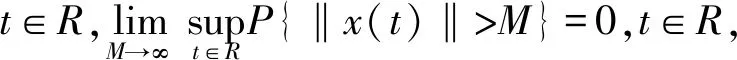
引理1.1[14]若为Caratheodory集值映射,且对任意给定的ψ∈B,SF,ψ={f∈L2(Rτ,H)∶f(t)∈F(t,ψ),t∈Rτ}是非空的,如果Γ∶L1(Rτ,X)→C(Rτ,X)为连续线性映射,则Γ∘SG∶C(Rτ,X)→Pcp,cv(C(Rτ,X)),x→(Γ∘SF)(x)=Γ(SG,x)是C(Rτ,X)×C(Rτ,X)上的闭图算子。
引理1.2[15]Γ∶B→P(B)是上半连续的凝聚多值映射,其中B是Hilbert空间H中的有界凸子集,若对任给的x∈B,Γ(x)是B中的凸闭子集,则Γ在B中有一个不动点。
2 主要结果
定义2.1.Θt适应随机过程{x(t)∶t0-r≤t≤T}称为问题(1)~(3)的温和解,当且仅当
讨论具有双参数发展系统的随机脉冲随机微分包含(1)~(3)解的可控性, 假定以下条件成立:
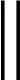
H4~H5类似于文献[16]。
定理2.1.假设条件H1~H5成立。如果
(4)
则系统(1)~(3)是可控的。
证明:定义如下控制:
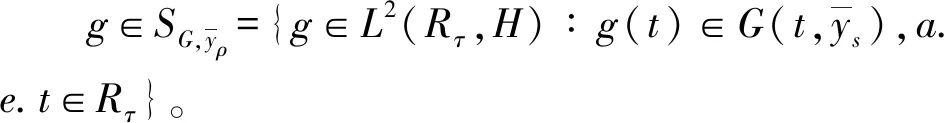
在赋予一致收敛范数的空间Y={u∈C(J,X)∶u(0)}=φ(0)上定义算子Γ∶Y→P(Y), 定义如下
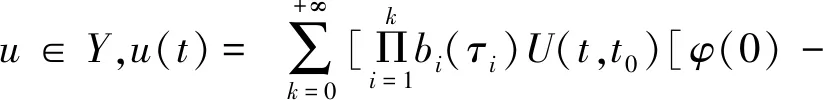
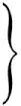
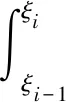
第一步,Γ将B中的有界集映射成有界集。
首先证明Γ1将B中的有界集映射成有界集。
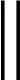
由此可得


同理可证明Γ2将B中的有界集映射成有界集,所以Γ将B中的有界集映射成有界集。
第二步,Γ2是全连续多值映射。
(ii) (Γ2B2)(t)={x(t)∶x∈Γ2(B2),t∈[t0,T]}是相对紧的。
t=t0时,Γ2(Br)(t)是相对紧的。当t0 令 因为U(t,s),(t>s)是紧的,Uε(t)={xε(t)∶u∈Γ2(Br),0<ε 当ε→0时,上式一致收敛于零。由此可知,存在相对紧集序列无限逼近于集合{u(t)∶u∈Γ2(Br)},所以,{x(t)∶x∈Γ2(Br)}是Y中的相对紧集。根据Arzela-Ascoli引理知Γ2是全连续集值映射。 第三步,Γ2有闭图。 证明u*∈Γ2(y*),其中yn→y*,yn∈Br,un∈Γ2(yn),un→u*,如果un∈Γ2(yn),则存在fn∈SF,yn,使得对任给的t∈[t0,T],有 接下来证明存g*∈Sf,y*在, 使得 利用时滞依赖状态及随机微分方程有关理论结合适当的多值映射不动点定理,在满足已知条件的基础上,先将随机脉冲随机微分包含转化成积分系统,然后按照所给不动点定理证明了具有一类双参数发展系统的随机脉冲随机集值微分方程解的可控性,此可控性的分析方法对同类集值微分系统解的可控性的研究具有一定的促进意义。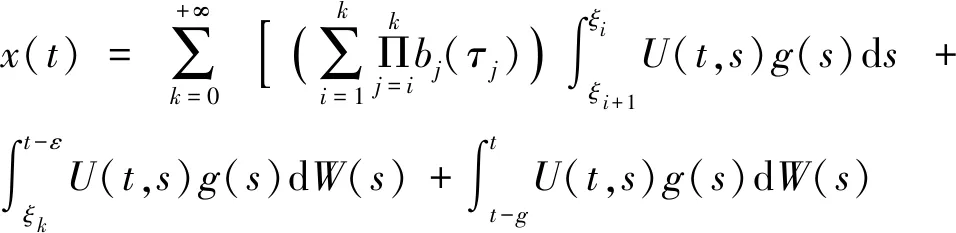
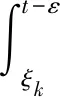
3 结语
