基于高速视觉的振动频率测量方法研究

丁美玲,陈慧蓉,方忠

(芜湖职业技术学院电气与自动化学院,安徽芜湖,241006)

振动在力学领域是一个十分重要的课题,它作为一种常见的自然现象存在于日常生活以及工业生产中[1]。在各种各样的工程以及生活中,振动是在所难免的,并可能因此产生许多危害。对于如何能更准确地测量振动,国内外已有很多学者进行了研究,并在各种工程实践中得到了非常广泛的应用[2]。

目前主流的振动测量算法主要有接触式测量和非接触式测量2 种方式。在接触式振动测量算法中,接触式传感器是必不可少的。由于接触式振动测量会直接改变接触物的结构特性,造成附加质量效应,因此,当待测物体的质量较轻时,测量误差会比较明显。此外,在对结构较大的物体进行振动数据的测量时,往往需要将大量的传感器安装在其结构表面,这样既耗时又费力[3]。除了上面所提到问题外,接触式的测量算法往往对测量环境等因素有比较严苛的要求。相比之下,非接触式测量算法拥有较好的包容性。

非接触式测量算法主要是基于视觉[4–6]和基于多普勒效应[7–10]等算法。近年来,视觉测量技术所应用的领域愈发广泛,并取得了良好的实验效果,尤其是在大型结构的振动检测方面[11]。Wahbeh 等[12]利用高精度摄像机对美国的Vincent Thomas 大桥桥墩进行竖向位移测量时,通过分析位移信号的频谱,得到了大桥振动的前两阶模态频率,此案例也表明在对大型结构进行振动测量时,基于视觉测量的算法是行之有效的方式。

一般情况下,普通相机(帧率一般为30 帧/s)在测量大型工程的振动频率时,其帧率即可满足基本的测量需要。当所要测量对象的振动频率较高时,普通相机则无法满足信息采集需求,从而导致振动信号失真。随着高速相机的应用逐渐普及,完整测量出拥有更高振动频率物体的振动信号将成为现实。

为了摆脱这种限制,国内外学者开发了许多可以拍摄1 000 fps 甚至更高帧率视频的高速相机。You等[13]将高速摄像技术与紫外带通滤光片相结合,得到了不同焊接条件下的高对比度紫外图像,并对焊接过程中飞溅物和火焰的特征和焊接质量之间的关系进行了研究,以此来监控金属焊接工作过程的稳定性。Rao 等[14]将高速视觉技术拓展到水下环境的振动位移测量。在地震激励下,通过高速视频来提取水下结构的振幅信息,并分析结构振动受到水下环境的影响程度,最后通过计算得到结构的自然频率和阻尼。雷秀军[15]对如何提取高速视觉测量系统信息的相关算法做了更加深入的研究,并成功地将其应用于叉车方向盘系统振动分析、恢复及螺栓损伤检测以及声音信号测量。

相较于传统视觉测量技术,应用高速相机的视觉测量技术所测量的范围更广,获取的信息量更大。因此,选取一种能够对高速振动特征进行提取的算法显得尤为重要。为了能够准确提取核心震动频率,本文设计一种新颖的分段定向寻优特征增强算法辅助MOSSE 滤波算法提取核心振动频率。

1 特征提取算法

1.1 分段定向寻优特征增强算法

受到拍摄时间短和光照不均匀问题影响,在高速视觉振动频率测量时往往会出现光影较暗处特征点弱化的情况(如图1(a)红色矩形框标记),导致二值化阈值设置过大时特征点丢失(图1(b)),阈值设置过小时出现大量噪声(图1(c)),不利于特征点振动位移提取及分析。为了解决这个问题,受到熵阈值法[16]解决自适应选择阈值的启发,设计了一种新颖的分段定向寻优特征增强算法。

图1 二值化效果图

首先,设置灰度图像为I,其中每个像素的值表示其亮度,将图像分成n个水平段,每个段的宽度为w,然后对每个段进行阈值化处理。

具体来说,对于第i个段,将其左边界设为xi,右边界设为yi,g(I)表示取图像I的总宽度,则有:

然后,计算每段像素值的最大值Mi和平均值ui:

其中,I(xi,yi)表示第i段图像,Si表示第i段图像的面积(宽×高)。

接下来,为每个段计算一个阈值Ti,这个阈值取决于该段的最大值和平均值,计算方式如下:

最后,将每段的像素值与对应的阈值比较,并将高于阈值的像素设为白色(255),低于阈值的像素保持原值,即当I(xi,yi)＞Ti时,点(xi,yi)的像素值为255。

总的来说,分段定向寻优特征增强算法能够有效增强特征点区域的像素,降低高斯降噪以及二值化后特征点丢失的概率,有效性实验见本文3.1 小节。

1.2 MOSSE 算法

由于MOSSE 滤波算法拥有极快的追踪能力,David S.Bolme 于2010 年首次提出来将MOSSE 滤波算法[17]应用在追踪领域,MOSSE 滤波原理如下。

假定fi、gi分别为训练目标样本和各样本所对应的期望输出。这些目标图像和期望输出的FFT 分别以Fi和Gi表示。MOSSE 滤波算法是为了在公式(6)中找到一个最优滤波器Hopt:

以文献[17]所描述的方法为例,通过等式(6)可以推导出Hopt的解析解其表达式如下:

因此,使用公式(7)可基于少量训练样本对滤波器做初始化处理,然后采用公式(8)～(10)在跟踪时对模板更新:

式(9)、(10)中μ表示学习率。这样就可以保存当前的Ai和Bi,对其进行更新时使用新的样本即可。

2 实验对象理论分析

本文以一根普通的钢锯条为实验对象,来验证基于高速视觉的振动频率测量方法是否具有一定的可行性。表1 为钢锯条的基础属性。将钢锯条的一端固定,另一端伸出桌面使之悬空。敲击钢锯条深处的一端,钢锯条受力持续振动。

表1 钢锯条材料与形状参数

悬臂梁的边界条件为Y(0)=Y′(0)=0,Y(L)=Y(L)=0。在此边界条件的基础上,悬臂梁弯曲振动时的特征方程为1 +cosβLchβL=0[1]。

因此,利用下式可算得该钢锯条悬臂梁模型的固有频率:

其中:ωi表示第i阶固有频率,E表示弹性模量,I表示截面惯量矩,ρ表示梁的密度,A表示截面积。获取实际钢锯条的基础属性值后,通过公式(11)计算得到本悬臂梁模型的前3 节固有频率分别为8.27 Hz、51.86 Hz。

3 高速视觉振动频率测量

为了方便在图像处理时捕获特征点,从钢锯条伸出端开始每隔5 mm 就涂上白色记号。图2 是由高速相机拍摄得到的部分帧的灰度图像,图像以大片灰色为背景,钢锯条用黑色线条状表示,白色点状为所作的标记。将钢锯条右端固定,左端受激励作用出现快速小幅振荡。由图1 可以明显看出,钢锯条的多阶振动被激出,振动比较复杂。

图2 高速相机拍摄的钢锯条振动情况的部分帧

3.1 图像预处理

首先,使用分段定向寻优特征增强算法处理高速相机拍摄的图像,处理结果如图3 所示,从图3 中可以看出,几乎所有的显著特征点都被强化,且没有出现明显的噪声干扰,证明了分段定向寻优特征增强算法的有效性和鲁棒性。

图3 分段定向寻优特征增强算法处理后的图像

然后,为了更有效地提取特征,将图像二值化处理。自适应阈值二值化方法是通过图像的局部特征自适应地设定阈值。但实验关注的是钢锯条振动的每一个特征点,所以本次实验采用全局固定阈值二值化方法,设定阈值为255。实验结果如图4 所示。

图4 分段定向寻优特征增强算法处理后再二值化的图像

3.2 特征点振动位移提取

为了方便提取钢锯条的振动位移并对其进行频谱分析,本文在第10 个点的周围绘制一个约为50×50 px 的感兴趣区域,由此便可绘制出该点附近的位移曲线。图5 为振动部分帧的灰度图像。

图5 MOSSE 算法振动位移提取部分帧

3.3 频谱分析

由于钢锯条横向振动信号太弱,本文仅对钢锯条的纵向位移做了频谱分析,并使用快速傅里叶变换将位移轨迹从时域转换到频域,其中第10 个特征点的位移曲线及频谱图如图6 所示。分析图6 可得特征点的振动频率,表2 为分析结果。结果显示,基于高速视觉的算法所得到的结果远比传统视觉算法所得到的结果更加接近理论分析结果,其最大误差仅为1.18%,证明该方法具有很强的可行性。

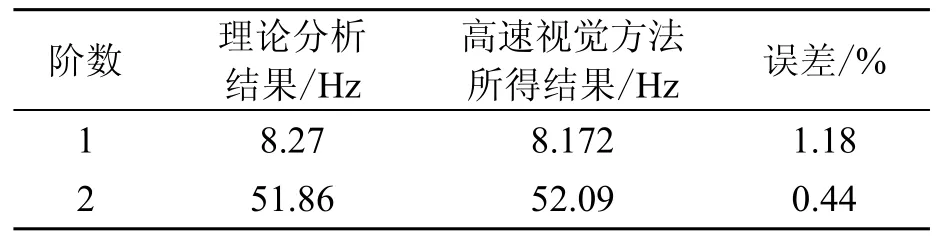
表2 基于高速视觉算法得到的结果与理论分析结果对比

图6 第10 个特征点的位移及频谱

4 结论

使用高速相机可以采集到更多有关振动对象的信息,但是传统的图像处理算法不能保证基于高速视觉的振动频率测量方法的实时性。因此本文设计了一种新颖的定向寻优特征增强算法辅助MOSSE 滤波算法提取悬臂梁的振动特征。通过与最先进方法的比较,定向寻优特征增强算法辅助MOSSE 滤波算法在高速视觉的振动频率测量方面取得了最佳结果,证明该方法具有很强的可行性和较好的鲁棒性。通过分析实验结果与理论计算结果,发现该方法具有更高的准确度,其最大误差仅为1.18%,优于传统视觉算法。