间歇性降雨作用下含碎石夹层堆积体水气运移规律
2023-10-17罗崎峰涂国祥
张 鑫,罗崎峰,涂国祥,唐 豪
(成都理工大学 地质灾害防治与地质环境保护国家重点实验室,成都 610059)
0 引 言
降雨入渗是水、气两种流体在土体或岩体孔隙中相互驱替的动态非饱和渗流过程。现有土体降雨入渗规律的研究大多都假设气压为恒定常数,忽略孔隙气对渗流的影响[1-3]。随着研究不断深入,不少学者发现降雨过程中孔隙气的存在会对土体渗透性以及入渗机理产生较大影响。Wu等[4]、郝霜等[5]、杨天娇等[6]考虑了气相对降雨入渗的影响作用,通过数值模拟进行了多相渗流耦合,总结出孔隙气压力随着降雨过程的变化规律,认为孔隙气的存在会影响雨水的入渗和迁移过程,对湿润锋的推进起到阻滞作用,并量化了边界透气性,发现稳定入渗强度与边界透气性呈对数关系。丁辉等[7]通过土柱水-气两相流试验,证明了孔隙气压力较小的情况更有利于土柱中水分入渗。
堆积体边坡由于其非均匀沉积特性,局部粗颗粒富集以及各类高渗透性夹层屡见不鲜,力学性质及渗透性往往与周围土体差异较大,因此降雨入渗过程更加复杂。物理模型试验是研究堆积体降雨入渗的常用手段,通过一维渗透仪与二维边坡降雨入渗试验,董辉等[8]提出了堆积碎石土湿润锋深度随时间的变化规律。Tu等[9]通过局部碎石富集堆积体的降雨入渗试验,发现富集的碎石土能为雨水渗入堆积体深部提供优势通道。针对含碎石夹层边坡,肖景红等[10]进行了降雨入渗数值模拟研究,认为碎石夹层为优势渗流层,雨水沿该层渗入坡体内部的深度显著高于沿坡面渗入的深度。
尽管目前对于堆积体降雨入渗已开展相当多的研究,但大多基于单相降雨渗流,较少涉及气液两相共同作用下的降雨入渗过程。天然情况下降雨过程会随时间不断变化,间歇性降雨时常发生,关于含碎石夹层堆积体在间歇性降雨条件下的水气两相运移规律的研究,目前还较为缺乏。为此,本文在降雨物理模型试验的基础上,考虑气相影响,并基于气液两相流基本理论,通过有限元数值模拟计算进行验证,对含碎石夹层堆积体在间歇性降雨条件下的渗流特性进行了深入探究。
1 研究区堆积体概况
研究区位于四川省甘孜藏族自治州泸定县,大渡河中游流域,地理坐标约为29°43′11.9″N、102°12′36″E。地处青藏高原东南缘的横断山脉,属于典型高山峡谷区,山体呈南北走向,第四纪堆积体在该地区有着广泛分布。经过调查,该区域堆积体内部普遍发育有不同物质组成的夹层,且具有明显的成层性。在磨西镇、东乐村、长沙坝村以及乌支索村等地堆积体中均发现有碎石夹层,这些夹层与上下土体在物质组成上差异明显,如图1。结合不同地点的调查资料发现,堆积体物质主要由角砾土以及碎石土组成。角砾土岩性以辉长岩和闪长岩为主,粒径范围200 mm≥φ>60 mm约占4%~10%,60 mm≥φ>20 mm约占10%~23%,20 mm≥φ>2 mm约占41%~50%,颗粒磨圆度差,多为棱角、次棱角状,角砾土具钙、泥质胶结,呈中密-密实状态;碎石土岩性以辉长岩、花岗岩为主,粒径范围200 mm≥φ>60 mm约占32%~41%,60 mm≥φ>20 mm约占25%~35%,20 mm≥φ>2 mm约占12%~24%,颗粒磨圆度较差,多为棱角、次棱角状,碎石土具钙、泥质中等胶结,呈稍密-中密状态,分选性和韵律性较差,局部有架空。碎石土大多以水平透镜状分布于堆积体内,层间粒径差异明显,出露的夹层厚度为0.2~1.8 m,发育位置为堆积体的中上部,最浅处距坡表约2~4 m。
研究区气候为典型的亚热带季风气候,全年四季分明,雨季集中在7—9月份,年平均降雨量538.7~672 mm,最大日降雨量63.2 mm,最大连续降雨天数为7 d,最大1 h降雨量25.8 mm。由于该地区堆积体碎石夹层发育,这类碎石夹层可能会对降雨期间堆积体内部水分、气体运移构成重要影响。
现场对长沙坝村堆积体采样进行颗分试验,取得颗粒粒径级配曲线,如图2所示。采用单环法原位试验测试了角砾土以及碎石土的饱和渗透率,并在实验室对试样的体积含水率和基质吸力进行测试,使用Van Genuchten[11]模型(简称VG模型)拟合得到水土特征曲线,如图3所示,VG模型拟合参数α、n、m取值见表1。根据Fredlund和Rahardjo[12]描述的方法计算得到非饱和渗透系数,从而得到非饱和渗透系数和基质吸力的关系曲线,如图4所示。
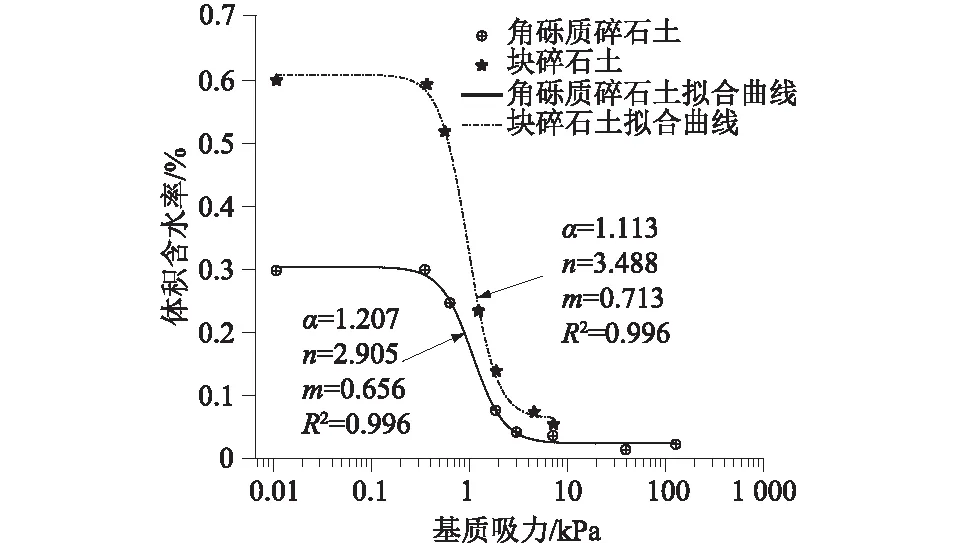
图3 水土特征曲线Fig.3 Soil-water characteristic curves
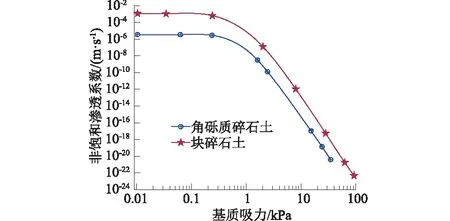
图4 非饱和渗透系数-基质吸力关系曲线Fig.4 Unsaturated permeability coefficient as a function of matric suction
2 含碎石夹层堆积体降雨试验设计
2.1 降雨试验装置
试验装置由模型箱、降雨系统及测量系统组成。模型箱尺寸为1.5 m×0.9 m×1.2 m(长×宽×高),边坡模型长1.5 m,宽0.9 m,坡顶高0.75 m,坡度35°,四壁连接处用玻璃胶进行密封处理,以隔水隔气;降雨系统由钢制支架、降雨喷头、增压供水箱、流量及水压表组成,通过改变水压和流量能够实现对降雨强度的控制;试验测量仪器有体积含水率、孔隙水压力以及基质吸力传感器各6套,埋设位置见图5。通过正面一台高清摄像机记录试验过程中堆积体变化情况。
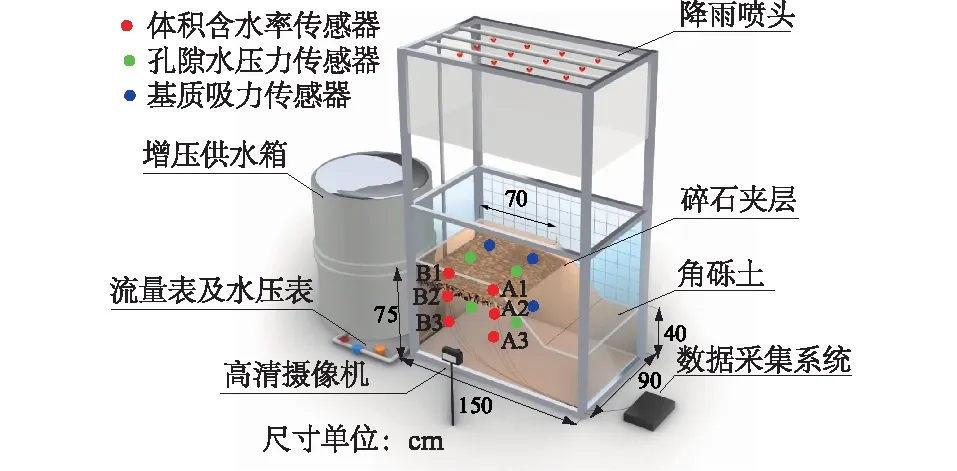
图5 试验设备布置Fig.5 Layout of test equipment
2.2 试验材料
根据堆积体现场调查情况,并考虑模型箱尺寸大小,将几何相似比Cl定为1∶10,重力加速度相似比Cg和密度相似比Cρ均为1∶1,按照量纲分析原理,确定重度相似比Cγ为1∶1、渗透系数相似比Ck为1∶3.16、黏聚力相似比Cc为1∶10、内摩擦角相似比Cφ为1∶1。
试验所用土体材料为原样土,为保证基质土与碎石夹层粒径差异,以及防止细颗粒粒径范围过小,采用等量替代法对碎石土粒径>3 cm、角砾土粒径>1 cm的土粒重塑,重塑后的试验土颗粒级配曲线如图2所示,原样土与模型土基本参数指标见表2。试验开始前按实测体积含水率3.0%和6.0%配置角砾土及碎石土。
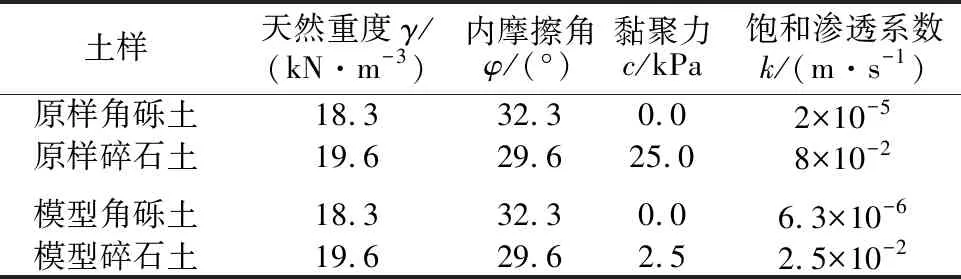
表2 土体基本参数指标Table 2 Basic parameters of soil
2.3 试验方案
根据泸定县实测降雨数据和《四川省中小流域暴雨洪水计算手册》设计了具代表性的间歇性降雨方案,采用人工模拟降雨的方式进行3次降雨,每次2 h,每场降雨间隔时间固定为1 d,即0、24、48 h为降雨开始时刻,总历时72 h。为保持在降雨时每场总降雨量相同,降雨强度均稳定在20 mm/h。由于每场降雨强度及降雨量较小、土体入渗速度较快,因此不考虑坡面积水或径流。
夹层展布形态保持与野外调查情况一致,即以水平层状分布碎石夹层为主,夹层位置靠近坡顶,距坡顶深度为15 cm,厚度为8 cm。堆积体分层堆填完成后,在夹层上下部埋入传感器,静置1 d待传感器数据稳定后开始试验。
3 试验结果与分析
3.1 降雨入渗过程
试验过程中相机记录到湿润锋变化过程,取每场降雨开始前后作对比,如图6所示。首场降雨开始后,雨水进入土体迅速扩散,逐渐形成连续的下渗锋面。湿润锋垂直向下推移,不同位置垂直下渗深度不均,经过2 h降雨后坡顶处下渗约14 cm,接近碎石夹层位置,坡脚处下渗约5 cm,如图6(a)。第一场降雨结束后湿润锋仍持续向下推移,此阶段由于缺少雨水补给,下渗速度逐渐衰减,但当雨水流经碎石夹层时,下渗速度陡然增加。第二场降雨开始前,坡顶以下湿润锋已基本经过碎石夹层,如图6(b),在降雨开始1 h内,坡顶湿润锋下移缓慢。原因在于前一次降雨停止后雨水仍向下迁移,因此上部湿润土体饱和度逐渐减小,再次降雨后雨水以稳定入渗率下渗,补充上部土体空间后才能达到先前湿润锋深度。在降雨持续1 h后,湿润锋推进速度加快,降雨结束后湿润锋在坡顶处下渗约10 cm,坡脚处下渗约7 cm,如图6(c),此时湿润锋形态呈“左陡右缓”的凸起状。第二场降雨结束后经过22 h,湿润锋整体向下推移约10 cm,如图6(d)。第三场降雨开始后湿润锋下移速度愈加缓慢,约1 h后坡脚湿润锋触底,并产生侧向入渗,降雨结束后坡顶以下湿润锋最大下渗约8 cm,最小约5 cm,如图6(e)。在72 h时试验结束,此时湿润锋右侧也已触底,中部凸起距底面约20 cm,如图6(f)。

图6 堆积体湿润锋变化过程Fig.6 Variation process of wetting front of deposit
3.2 传感器结果分析
降雨过程中各测点传感器读数变化趋势如图7,第一场降雨开始24 min后,坡顶以下10 cm深度处的A1、B1测点相继响应,两测点的体积含水率与孔隙水压力变化趋势基本相同,均在降雨开始后迅速增长,随降雨结束而逐渐回减。在经过2 h降雨后,A1、B1测点最大体积含水率分别为18.2%和17.1%,最大孔隙水压力分别为2.15 kPa和2.08 kPa。两测点基质吸力在降雨后不断波动并缓慢增长,在遇水后急剧下降,分别降至17 kPa与19 kPa后趋于稳定。第二场降雨开始后,A1、B1测点先后响应,体积含水率及孔隙水压力增长趋势与首场降雨后增长趋势相同,但第二场降雨后体积含水率峰值要大于首场降雨下的峰值,分别达到20.3%和18.9%。B2、A2测点分别在24 h 19 min和25 h 39 min响应,B2测点体积含水率同样为陡增后迅速回减的变化趋势,A2测点体积含水率缓慢增长,在36 h后达到8.7%。B2测点基质吸力随降雨开始首先响应,30 min后A2测点响应并骤降至13.3 kPa。第三场降雨开始前,A1、B1测点体积含水率稳定在10.9%,孔隙水压力稳定在1.84 kPa左右,A2、B2测点体积含水率分别稳定在9%和7.8%左右。第三场降雨开始后,以上4个位置测点在1 h后响应,响应时间略有滞后,随后在51 h 5 min时B3测点响应,体积含水率陡然增大至13.2%后骤降,孔隙水压力经过12 h后由0.54 kPa增长至1.1 kPa。53 h 20 min时A3测点响应,直到试验结束,体积含水率增长至6.8%。

图7 体积含水率、基质吸力和孔隙水压力的变化过程Fig.7 Variation processes of volumetric water content,matric suction and pore water pressure
可以发现,各测点传感器响应顺序与模型箱侧面观察到的湿润锋运移过程基本一致。传感器数据变化趋势表明,首场降雨时,雨水受重力、毛细管力以及分子力的共同促进作用,下渗速度最快。降雨结束后,土中水继续向下迁移,湿润土体由暂态饱和状态逐渐变为非饱和状态,堆积体内部经历饱和区向非饱和区渗流补给的饱和度再分布过程。由于上部浸润土体饱和度逐渐降低,含水量梯度减小,使得土壤水分作用力减小,因此下渗减缓。后两场降雨边坡土体含水量重新分布,雨水入渗在已浸润土体的基础上进行,由于基质吸力的减小,雨水在浸润土体中入渗主要由重力驱动,入渗速率均低于首场降雨,因此饱和度再分布过程中湿润锋推进存在滞后性。
4 含碎石夹层堆积体水气运移规律数值模拟
4.1 模型建立与计算参数选取
基于水气二相流渗流理论[13],通过有限元软件对含碎石夹层堆积体的降雨入渗进行数值模拟计算,并设置均质堆积体作为对照组。为了有效建立非饱和土水气二相流渗流模型,作出如下基本假设:土体孔隙中液体及气体的流动是由各自的压力梯度引起的,并均遵从达西定律[14];忽略水土特征曲线的滞后性质;气液两种流体占据了土体孔隙,且孔隙间相互连通。
图8为二维有限元计算网格模型,分别在模型中设置6个监测点,监测点位置对应物理模型试验传感器埋设位置。模型边界条件设定为:底面Pw=-ρgy,两侧边为无流通边界,上部为降雨边界qw=q,模型内初始孔隙气压力为标准大气压Pa=Patm,坡表边界为气体流通边界(以上各式中,Pw为底部边界压力;qw为上部边界流量;q为降雨强度;Pa为初始孔隙气压力;Patm为标准大气压)。数值计算中使用的模型土体基本物理参数由前述试验取得,除此之外,气相和液相的基本参数如表3所示。

表3 数值计算气相和液相的参数Table 3 Numerical calculation parameters of water-airtwo-phase
4.2 数值模拟结果与分析
通过追踪土体饱和度变化情况,得到有无碎石夹层2种堆积体内部湿润锋迁移过程如图9所示,并与物理模型试验结果对比。在考虑孔隙气压力影响下,均质堆积体在首场降雨开始2 h后湿润锋均匀向下推进12 cm,在第二次降雨24~26 h湿润锋下移5 cm,第三次降雨48~50 h湿润锋下移约4 cm,入渗速度随着降雨场次增加呈逐渐递减趋势。

图9 湿润锋迁移过程Fig.9 Migration of wetting front
数值模拟结果显示,含碎石夹层堆积体湿润锋在首场降雨结束后下移约12 cm,24~26 h湿润锋下移约8 cm,48~50 h湿润锋向下推进5 cm,经过72 h后坡顶处湿润锋下移56.8 cm。物理试验中首场降雨结束后坡脚处湿润锋向下移动4 cm左右,坡顶处下移约15 cm,24~26 h坡脚处湿润锋下移7 cm左右,坡顶处下移约15 cm,48~50 h坡脚处湿润锋向下移动约5 cm,坡顶处下移10 cm左右,经过72 h后坡顶湿润锋下移62 cm。含碎石夹层堆积体边坡数值模拟结果与物理试验中湿润锋变化曲线虽有区别,但整体趋势及最终下渗深度基本相同。
取3条研究截面L1、L2、L3(如图9),对各截面数据汇总得到不同时间降雨入渗深度、入渗速率与时间的关系,如图10所示。
对于含碎石夹层堆积体,L3截面处入渗速率在2 h左右达到最大值,随后经历陡降。在雨水到达碎石夹层位置后,雨水入渗速率瞬时增大,于13 h左右增长至峰值4.7 cm/h,在经过夹层后入渗速率陡然降至最低。第二场降雨后,两模型入渗速率的增长均存在一定滞后性,在26 h左右含碎石夹层堆积体入渗速率再次增长,最大至1.9 cm/h左右,在此时刻均质堆积体内入渗速率却未有相同涨幅。在第三场降雨后,两模型入渗速率均无太大涨幅,均质和含夹层堆积体入渗速率均值分别保持在0.39、0.44 cm/h左右,但含碎石夹层堆积体在降雨结束后总入渗深度大于均质堆积体。间歇性降雨条件下,首场降雨过程中土体入渗速率最高,后两场降雨入渗速率明显降低。表现为初期入渗深度陡增而后逐渐衰减,越往深处雨水下渗越困难,且随着总入渗深度的增加,再次降雨对入渗速率的增长作用不明显。
图11给出了两组模型中6个监测点记录的孔隙气压力变化与时间的关系曲线。由图11可知,每场降雨各监测点孔隙气压力增长趋势基本相同,表现为随降雨过程不断增大,在降雨结束后逐渐减小并接近标准大气压,且表层消散速度较快。每场降雨后,两模型表层的A1、B1监测点孔隙气压力峰值到来时间最早,但数值稍有减小。每场降雨后位于夹层以下的传感器孔隙气压力峰值则呈阶梯式提升,入渗越往深部孔隙气压力峰值越大。值得注意的是,后两场降雨后均质堆积体孔隙气压力增长速率明显大于含碎石夹层堆积体,孔隙气压力峰值也更大。在后两场降雨后的孔隙气压力消散阶段,含夹层堆积体内A2、B2监测点孔隙气压力减小速度快于均质堆积体。

图11 孔隙气压力与时间关系曲线Fig.11 Time-history of pore air pressure
2组试验孔隙气压力均在3、30、54 h附近时增长至极大值,表明降雨结束后孔隙气压力并不会及时消散,孔隙气压力到达峰值存在一定滞后性。2组模型孔隙气压力增长至峰值时的气压分布如图12所示。首场降雨后,湿润锋的推进向下挤压空气,2组模型中坡脚处的孔隙气压力最大,如图12(a)、图12(b)。在第二次峰值到来时,均质堆积体中的孔隙气压力重新分布,此时坡脚处的气体逐渐右移,沿坡表向内均匀分布,如图12(c),而含夹层堆积体孔隙气压力则集中在坡脚及坡中位置,且数值上小于均质堆积体,如图12(d)。孔隙气压力到达第三次峰值时,均质堆积体孔隙气压力集中在坡顶靠右位置,最大孔隙气压力可以达到104.6 kPa,如图12(e),此时的含夹层堆积体内孔隙气压力集中在坡顶靠左侧,并与夹层左侧有一定连接,孔隙气压力最大处仅104.2 kPa,如图12(f)。从空气运动矢量箭头可以看出,均质堆积体内各时刻空气沿坡表分散逸出,而含夹层堆积体内部空气先向碎石夹层集中,再沿着该夹层向坡表薄弱处逸出,气体迁移存在一定集中性,坡表其他位置空气流通量相应减小。
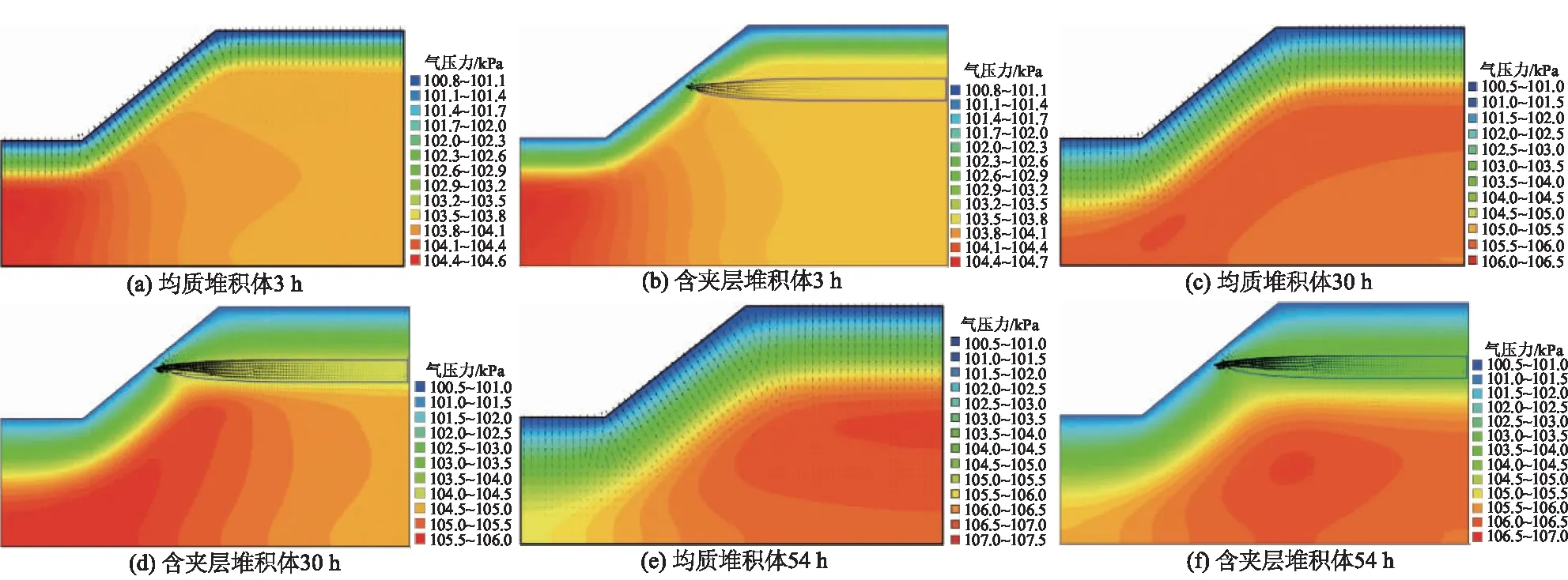
图12 孔隙气压力分布云图Fig.12 Contours of pore air pressure
4.3 水-气传导过程及机制分析
降雨在边坡中的传导过程是雨水渗入土体孔隙,从而驱逐气体排出的运动过程,在降雨充足的情况下,坡表土体液相饱和度迅速增大,逐渐形成连续的暂态饱和区。暂态饱和区不断向下扩展,气体无法及时排出,由于气体的可压缩性大于液体,因此下移的水分会迫使气体不断压缩,而不断累积的气压会形成反方向的顶托力从而阻缓雨水下渗。对土体水分剖面取一土柱作受力分析,假设土体表面无积水,雨水入渗后土体完全饱和,水分垂直向下传导,则土体表面作用有大气压力Patm;饱和区内水的重力方向向下,由于水重与暂态饱和区深度有关,因此用暂态饱和区深度h表示其大小;饱和区与非饱和区交界处存在方向向下的毛细管力,以毛细管上升高度hc表示;非饱和区受下渗水的挤压后的孔隙气压力Pa,其与大气压的差值也可用相当的水柱高度表示。因此作用在土柱上的合力H为
H=h+hc-(Pa-Patm) 。
(1)
在降雨过程中碎石夹层对土体内部气体排出起促进作用,由于孔隙率较大,在非饱和状态下为气体逸出提供了天然优势通道。间歇性降雨过程中,土中气体经历压缩—释放的循环过程,此过程中含碎石夹层堆积体与均质堆积体相比孔隙气逸出速度更快,而孔隙气压力消散速度差异的影响直接体现在降雨入渗速率和入渗深度上,且越往深处湿润锋推进受到孔隙气压力阻缓影响越明显(图13)。
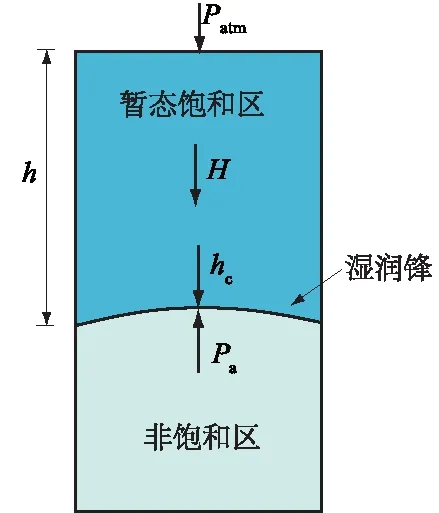
图13 水-气传导机制Fig.13 Water-airconduction mechanism
5 结 论
本文通过对含碎石夹层堆积体的现场调查,建立了降雨入渗物理模型试验,并结合有限元仿真软件进行数值计算验证,结果表明:
(1)间歇性降雨条件下,每场降雨结束后堆积体内部经历暂态饱和区向非饱和区补给的土体饱和度再分布过程,后续降雨在前一场基础上进行,因此湿润锋的推进具有一定滞后性。
(2)每场降雨过程中土中气体经历压缩-释放的循环过程,降雨结束后孔隙气压力并不会及时消散,堆积体中孔隙气压力到达峰值存在一定滞后性,含碎石夹层堆积体总体孔隙气压力较低且在降雨停止后孔隙气压力消散较快,孔隙气压力消散速度差异的影响,直接体现在垂向入渗速率上。
(3)湿润锋的推进在土体浅表层受孔隙气压力影响不大,而越往深部,湿润锋推进速度受孔隙气压力影响越明显。相较于均质堆积体,含碎石夹层堆积体入渗深度增加的重要原因在于碎石夹层为气体逸出提供的优势通道,孔隙气体向该层聚集并沿坡表薄弱处排出。在此作用下,堆积体内部孔隙气压力总体较小,有利于雨水下渗。
本研究分析了含碎石夹层堆积体降雨入渗的水气运移特征,结果可为进一步探讨该类型边坡在降雨条件下的失稳破坏提供参考。
