基于Kriging法的造斜率预测精度提升研究*

2023-10-17潘勇博

石油机械 2023年10期

潘勇博张红冯定冯云

(长江大学机械工程学院；湖北省油气钻完井工具工程技术研究中心)

0 引言

石油钻探行业中，随着技术的不断进步，旋转导向钻具已成为相关工作者的最佳选择之一[1-2]。造斜率作为导向钻具的一个重要参数，常被用于衡量导向钻具的造斜能力。实际钻探过程中，造斜率影响因素众多，如地层硬度、钻头、导向工具结构[3]、温度及压力等。迄今为止，在无数学者的不懈努力下，已经涌现出许多造斜率预测法。比较有代表性的有H.KARLSSON等[4-5]于1985年提出的三点定圆法、M.BIRADES等[6-7]于1989年提出的平衡曲率法、苏义脑[8]于1992年提出的极限曲率法。此外，还有修正的三点定圆法[9-10]、钻头与地层相互作用理论[11]和回归分析法[12]等也能较好地预测造斜率。几何预测法虽然计算简单，但是仅考虑了钻具组合的几何结构，忽略了地层因素和工具材料的影响，预测精度已远远不能满足当今的生产需求。与几何预测法相比，力学预测法的预测精度有了大幅度提升，但计算复杂度要远远高于其他预测法。而回归分析法中的Kriging代理模型预测法能够通过已有的钻井数据构建一个响应面模型，用该模型对目标点进行插值计算[13-14]，获取目标点处的预测造斜率，以此来指导钻井作业。前期研究发现[15-16]，Kriging代理模型能够高效地处理“多变量单响应”问题，且预测精度要优于一阶多项式模型、二阶多项式模型以及RBF模型，对于钻探行业中多因素影响下的造斜率预测具有较好的预测结果。

本文在前期对于Kriging代理模型研究的基础上，将统计学中相关性这一概念加以运用，以便提高Kriging代理模型的预测精度。基于四川省某井段钻井参数，计算造斜率与各个影响因素之间的相关系数，剔除相关系数处于(-0.2，0.2)区间内的“无关因素”后，用剩余的影响因素(敏感因子)再次进行数据拟合并进行造斜率预测，并与未经数据处理的Kriging代理模型预测结果对比，结果显示：剔除“无关因素”后的预测模型不仅能够大幅度降低计算量，更能够在原有预测模型的基础上提高预测精度，在一定程度上降低钻探过程中钻头偏离目标地层的风险。

1 Kriging代理模型构建

Kriging代理模型又被称为Kriging响应面模型，它的产生依赖于Kriging插值法。Kriging插值法是基于地理学第一定律所衍生出来的插值方法，核心思想是空间内任何一点处的响应值与其附近若干个已知点的响应值有关，并且该点与已知点的相关程度与距离有关[17-18]。此插值法可表示为：

(1)

式中：y(xi)表示第i个已知位置处每100 m的实际造斜率，(°)；λi表示第i个已知位置的造斜率对待估位置造斜率的影响程度，通常为距离的某种函数；y(x0)表示待估位置处每100 m造斜率的预测值，(°)。

为了得到待估点的预测造斜率y(x0)，必须求出系数λ。为此，引入统计学中“将未知函数看作是高斯静态随机过程的一个具体实现”的假设，此假设可表示为：

Y(x0)=m+p(x0)

(2)

式中：m为一个常数，它表示空间某个区域内造斜率的数学期望，反映了待估造斜率的整体趋势；p(x0)可以理解为待估位置处造斜率偏离其数学期望的程度，反映了待估造斜率的局部波动。实际问题中，p(x0)的数学期望为0，方差为σ2；Y(x0)表示目标位置每100 m造斜率预测值，(°)。

由地理学第一定律可知，一定范围内，空间内不同位置处的响应值(本文释义为造斜率影响因素的不同取值组合所对应的造斜率)具有一定的相关性，根据统计学中协方差相关理论不难得出：

(3)

即

Cov[p(x0)，p(x1)]=σ2R(x0，x1)

(4)

式(4)中，变量R表示影响因素的不同取值组合所对应的造斜率的相关程度，常用高斯指数模型来拟合。

为使造斜率预测模型具有更高的预测精度，Kriging插值法要求预测结果的均方误差SMSE最小，即求出合适的权重系数，使得下式取到最小值：

SMSE[y(x0)]=E{[y(x0)-Y(x0)]2}

(5)

(6)

经过运算，最优权重系数λi可由矩阵形式的线性方程组求出：

(7)

为方便表述，将式中：

记为矩阵R，R为对称矩阵。

将(1 1 … 1)T记为矩阵M；将(R(x1，x0)，R(x2，x0) …R(xn，x0))T记为矩阵r；将(λ1λ2…λn)T记为矩阵λ；于是上式变为：

(8)

即有：

(9)

将式(9)代入Kriging插值法的定义式，即可得到：

(10)

式中：y=(y1，y2，…，yn)T。

进一步简化后可写为：

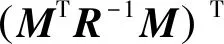
rTR-1{y-[(MTR-1M)TMTR-1y]M}

(11)

在最终表达式中，除了矩阵r以外的所有参数仅与训练样本有关，在实际使用过程中可在首次计算完成之后将训练好的造斜率预测模型存储下来。预测不同待估点造斜率时仅需计算并代入矩阵r即可得到造斜率预测值。

2 造斜率预测模型优化

前期研究的Kriging代理模型在预测造斜率前仅对获取到的造斜率影响因素与实际造斜率进行拟合，并未对数据进行任何处理。在前期研究中虽已验证Kriging代理模型的预测精度要优于一阶多项式模型、二阶多项式模型以及RBF模型，但在钻探行业不断发展的今天，井眼轨迹的控制面临着更大的挑战，基于Kriging代理模型的造斜率预测精度仍有待提高。

在实际问题中，多因素问题比比皆是，如农作物产量、电子产品使用寿命、钻井时实际造斜率等。而各个因素对于响应值的影响效果各不相同，甚至有些因素对于响应值几乎没有影响。在信号处理中由于噪声信号的存在使得人们很难获取期望的输出，在造斜率预测方面也存在相似问题，即钻井作业时，影响实际造斜率的因素众多，如钻头侧向力、钻头偏转角以及邻井造斜率等。在获取的初始数据中，有些影响因素对造斜率的影响效果较为显著；而有些因素对于造斜率的影响甚微，倘若将这些“噪声因素”也作为回归拟合的自变量之一进行数值计算，不仅不能得到精准的拟合方程，甚至会使样本点变得更加离散。因此，考虑剔除相关系数过低的因素，用剩下的敏感因子进行数据拟合并进行插值计算，以获取精度更高的造斜率预测模型。

2.1 现场数据预处理

构建造斜率预测模型时，有些因素的取值普遍较小，而有些因素的取值普遍较大。输入的各个影响因素的数量级可能会影响造斜率预测精度，为了降低由各因素的数量级带来的误差，本文采用MinMaxScaler法对造斜率影响因素的实钻数据进行归一化处理，使所有数据均分布于区间[0，1]。MinMaxScaler归一化的计算式为：

(12)

式中：x′为经过归一化处理后的变量；x为变量初始值；xmax、xmin分别为初始变量中的最大值和最小值。

2.2 现场数据相关性分析及数据加权变换

造斜率影响因素众多，通过已知钻井数据求出各个因素与实际造斜率间的相关系数，分析实际造斜率对各个影响因素的敏感程度。变量间的相关系数有多种定义方式，如Pearson相关系数、Spearman相关系数等。本文采用Pearson相关系数，其计算式为：

(13)

式中：rX，Y为某个影响因素X与造斜率Y之间的相关系数，取值范围为[-1，1]，其绝对值越接近1，表示2个变量X、Y之间的线性相关程度越高；Cov(X，Y)为变量X、Y间的协方差；E(X)、E(Y)、D(X)、D(Y)分别为变量X、变量Y的均值和方差。

利用Pearson相关系数评估各个影响因素与造斜率之间的相关性，依据相关程度表[19]剔除相关系数处于(-0.2，0.2)间的无关变量，将其余的变量作为敏感因子，分别按下式进行加权处理。

(14)

式中：r(x，i)y为第i个影响因素与实际造斜率之间的相关系数；n为参与构建预测模型的敏感因子个数；xi0为第i个未经加权处理的敏感因子；xi为第i个加权处理后的敏感因子。

不同相关系数对应的相关程度如表1所示。

表1 不同相关系数对应的相关程度Table 1 Correlativity corresponded by different correlation coefficients

2.3 造斜率预测精度评估标准

一个预测精度不足的模型对于实际生产需求毫无意义，因此，如何选取一个合适的标准来评判预测精度显得尤为重要。本文由于样本点较少，使用单个指标来评判Kriging模型的预测精度时，会因为个别特殊样本点的存在使得预测结果缺少可信度。为了克服这个缺点，本文继续采用文献[16]中的3个预测指标(均方根误差(ERMS)、最大绝对误差(EMA)和平均绝对误差(EAA))综合评判预测模型的精度，计算式为：

(15)

用这3个误差的均值作为最终衡量依据，误差越小则预测模型的精度越高。

3 案例分析

为了验证相关性分析后的Kriging代理模型能否提高造斜率预测精度，采用文献[20]中四川省某井段钻井参数进行预测模型构建。钻井参数如表2所示。

表2 四川省某井段钻井参数Table 2 Drilling parameters of a hole interval in the Sichuan Basin

部分钻井参数示意图如图1所示。

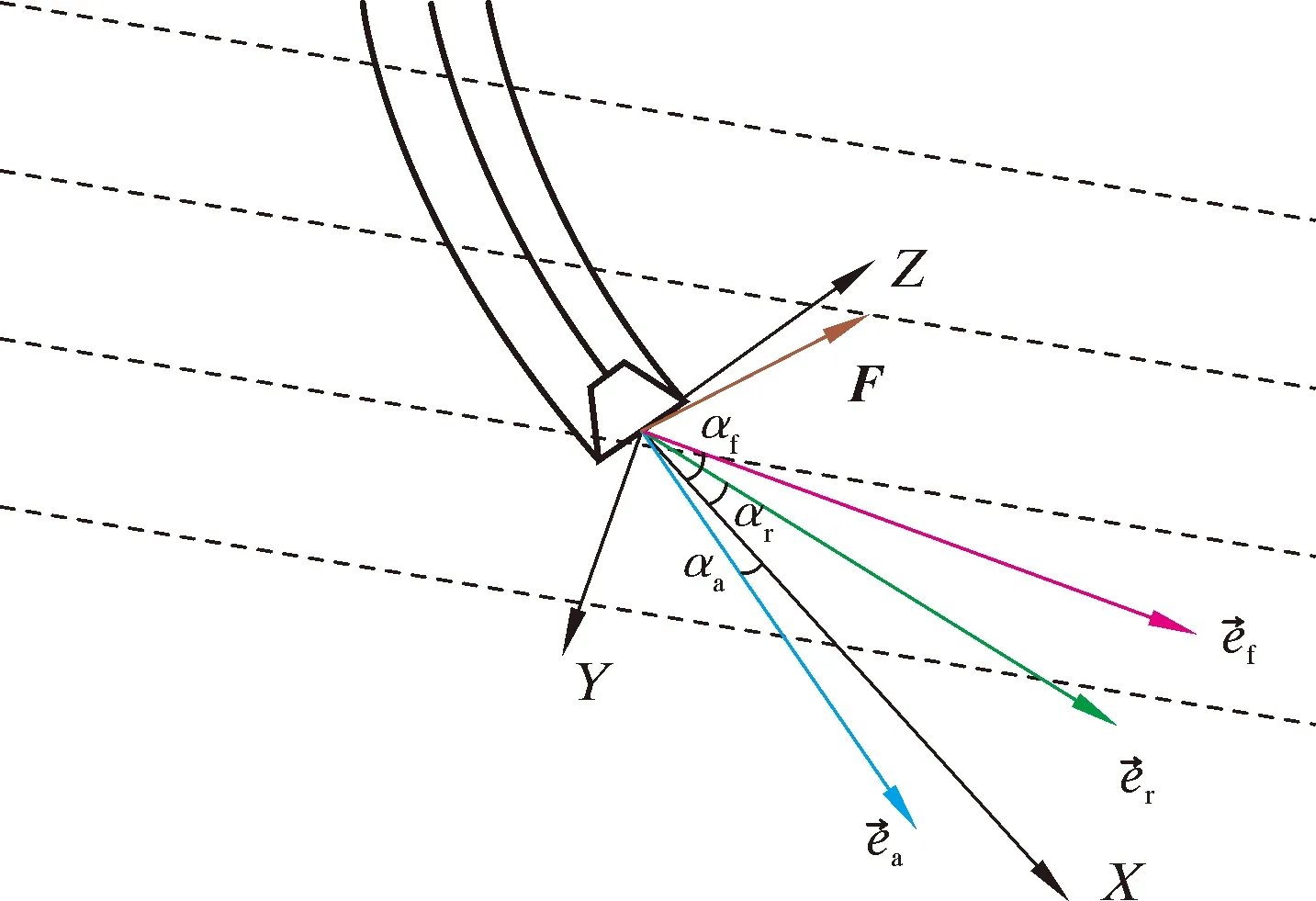
图1 部分钻井参数示意图Fig.1 Schematic diagram of some drilling parameters

图1中，X、Z分别指向井眼轴线的切线方向和井眼高边方向；X、Y、Z共同构成笛卡尔坐标系，以此确定Y的指向；向量ef、er和ea分别指向钻头合力方向、实际钻进方向和钻具轴线方向；F为钻头侧向力；αa为钻头偏转角、αf为钻头合力角、αr为钻进趋势角。

3.1 钻井参数预处理

为了降低由样本数据分布区间差异造成的造斜率预测精度不足，采用MinMaxScaler法对样本数据进行归一化处理。由于对初始参数中钻头侧向力、钻头偏转角、钻头合力角、邻井造斜率以及初始井斜进行了归一化变换，其物理意义已不再是对应的钻井参数，但在某种意义上能够反映对应的钻头侧向力等钻井参数。故将变换后的钻头侧向力、钻头偏转角、钻头合力角、邻井造斜率以及初始井斜分别记为X1、X2、X3、X4、X5。归一化后的钻井数据如表3所示。

3.2 钻井数据相关性分析及加权变换

该数据集仅有26个样本，为了同时实现模型构建及造斜率预测，由程序随机抽取其中22组数据构建造斜率预测模型，用剩余的4个样本检验模型的精度。由于不同的训练样本得到的预测模型精度不同，重复试验300次，选取预测精度最高的预测模型作为最终输出结果。下文涉及到的计算数据为最优预测模型对应的计算结果。

首先运用统计学相关理论分析该数据中各个影响因素与造斜率之间的相关性，得出对应的相关系数，相关性分析结果如表4所示。

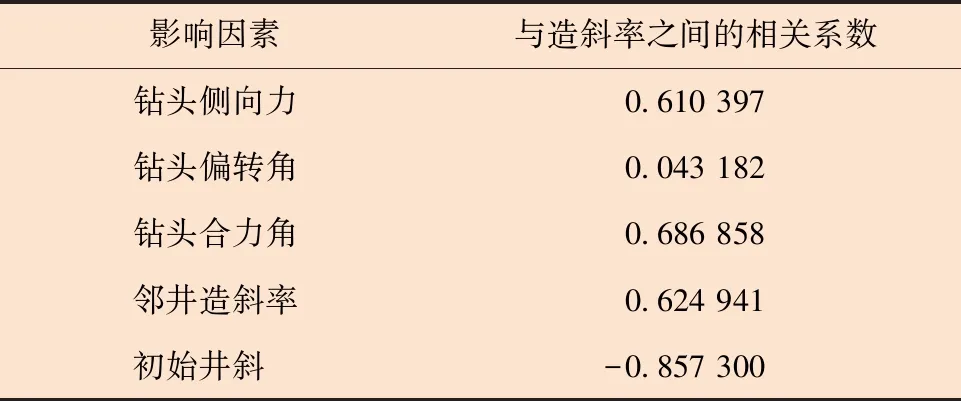
表4 各影响因素与造斜率之间的相关性分析结果Table 4 Correlation analysis results between influential factors and build-up rate

表4中，相关系数表示各个影响因素与造斜率之间的相关性大小，其绝对值越接近1，表示相关程度越高[21-22]。

为了直观地比较相关性分析结果，将表4中各个数据转化为柱状图，如图2所示。从图2可以直观地看出，钻头偏转角与造斜率之间的相关程度最低且相关系数仅为0.04，故可以将其看作“无关变量”处理。将该因素剔除后用剩余的4个敏感因子再进行模型构建。此处结论与文献[19]中基于神经网络预测法的分析结果一致。

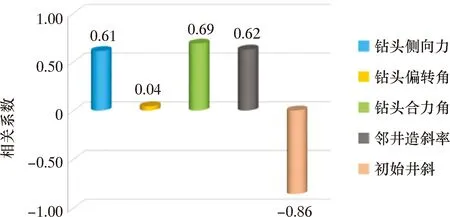
图2 各影响因素与造斜率之间的相关系数柱状图Fig.2 Correlation coefficients between influential factors and build-up rate

剔除了无关变量之后，将剩余的4个敏感因子X1、X3、X4及X5根据下式进行加权变换：

(16)

式中：X1、X3、X4及X5分别表示经过加权变换后的4个敏感因子；X10、X30、X40及X50分别为对应于X1、X3、X4及X5加权变换前的敏感因子。

对数据进行加权变换后即可代入数学软件构建预测模型。用于构建预测模型的最终数据见表5。

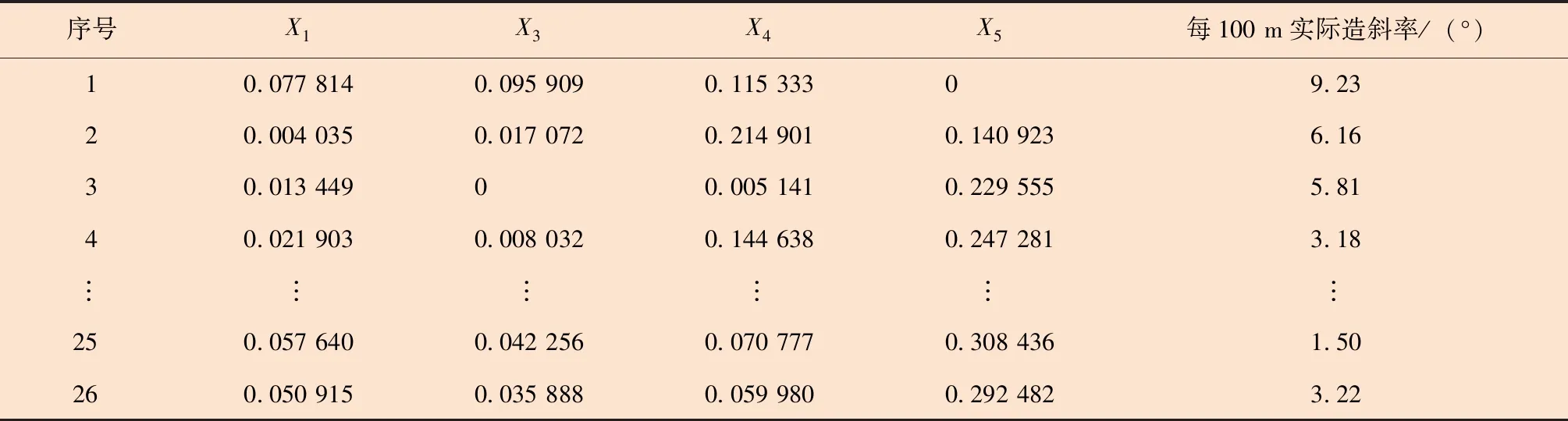
表5 用于构建预测模型的最终数据Table 5 Final data for building prediction model

3.3 造斜率预测及精度分析

为了做对照，本文先采用初始数据(5个影响因素)中22个样本构建Kriging代理模型，并将剩余4个样本代入预测模型进行造斜率预测；随后，用表5中经过多种处理后的数据(剔除无关因素

并进行数据处理后的数据集)重复上述操作，并与未经数据处理的预测模型进行预测值对比。由于撰写需要，下文中的所有计算结果仅保留两位小数。造斜率预测结果如图3所示。

图3 优化前、后的Kriging法造斜率预测值Fig.3 Predicted values of build-up rate using Kriging method before and after optimization

从图3可以看出，在4个用以测试的样本点处，相较于使用初始数据进行模型构建，经过相关性分析后的Kriging代理模型能使造斜率预测值更接近实际值。其中，在各个用于测试的“待估点”处，造斜率预测偏差(预测值与真实值之差的绝对值)如图4所示。

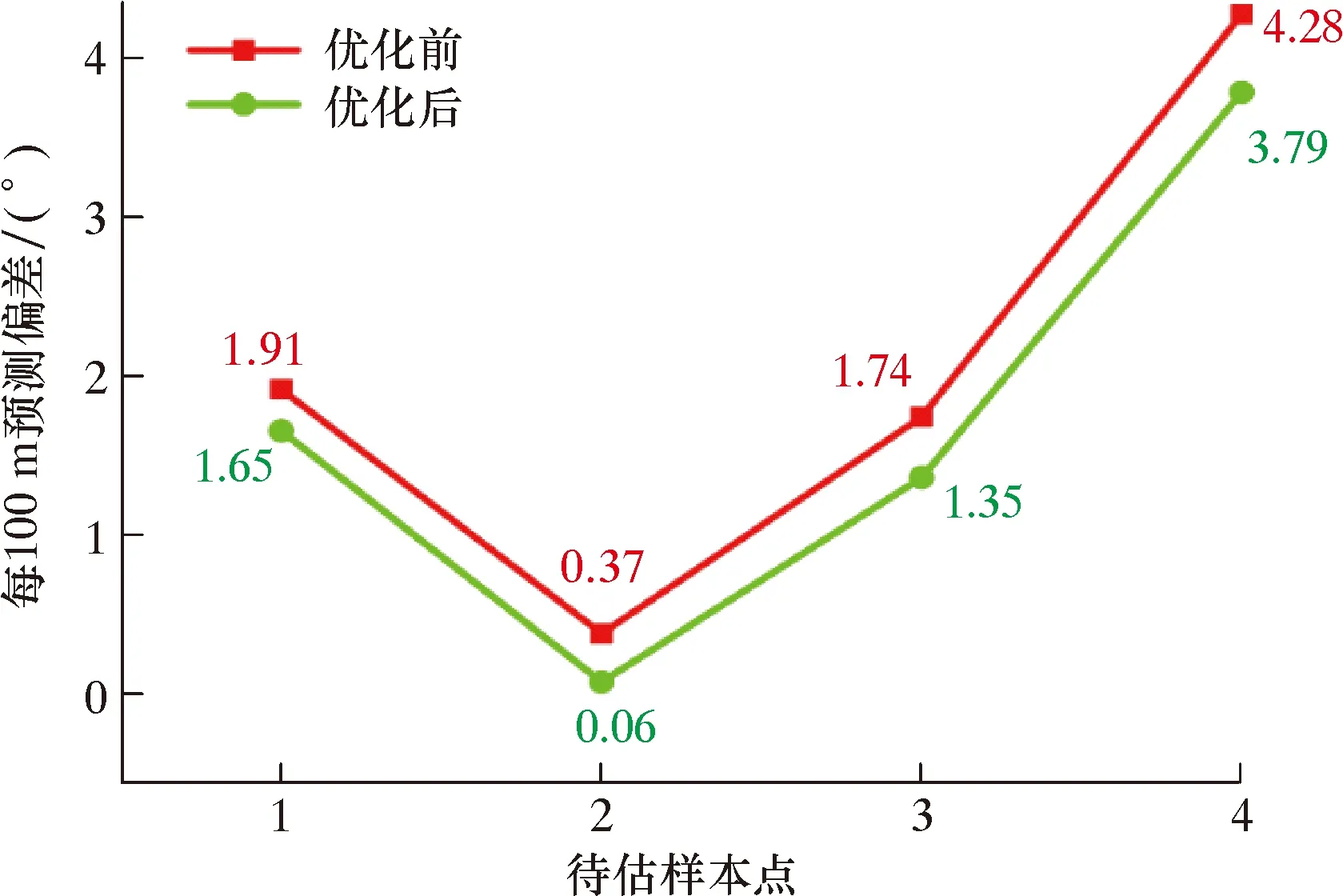
图4 优化前、后的Kriging法造斜率预测偏差Fig.4 Prediction deviations of build-up rate using Kriging method before and after optimization

从图4可以看出，剔除“无关因素”之后构建的Kriging代理模型的预测误差要低于用原始数据构建的Kriging代理模型。但实际造斜率越趋近于造斜极限，造斜率预测值偏离实际值的程度越大。究其原因，主要是训练样本点过少，随着越来越多高影响因素的加入，该模型的预测精度将会进一步提升。

由于待估点过少，仅采用待估点的预测偏差判断模型优劣可能会使试验不具备说服性。考虑到文献[16]中使用了ERMS、EMA和EAA等3个指标来判断模型的预测精度，本文继续采用这3个指标，以此来增加试验结果的可信度。试验结果如图5所示。

降低误差等效于提升精度。为了更加直观地看出此方法对预测模型预测精度的提升效果，将预测精度提升率(误差的降低值与改进前的误差值的比值)以百分比的形式表示，结果如图6所示。

由图5和图6可以看出：剔除“无关因素”前均方根误差、最大绝对误差、平均绝对误差及3种误差平均值分别为2.51、4.28、2.07及2.95；剔除“无关因素”后均方根误差、最大绝对误差、平均绝对误差及3种误差平均值分别为2.17、3.79、1.71和2.56；相较于用初始数据构建的Kriging代理模型，改进后模型的3种误差RMSE、MAE及AAE分别降低了13.26%、11.53%和17.37%，3种误差的平均值降低了13.39%。由此可知，剔除“无关”因素之后再构建Kriging代理模型，预测误差能降低13.39%，即预测精度能得到有效提升。

4 高精度Kriging预测模型应用流程

任何工程研究起源于工程问题也要应用于工程问题。实际钻探过程中可以通过检测钻头所在位置，从而得知井眼轨迹是否偏离了目标地层，然而这样做的弊端也不容忽视，即当检测到井眼轨迹偏离目标地层后，此时已酿成工程事故，工作人员能做的也仅仅是补救。

本文所探讨的造斜率预测方法能够在钻井作业时实时预测下一时刻的造斜率，通过提前设置目标地层所在位置和传感器返回的钻具当前位姿，综合计算钻具钻入目标地层所需的造斜率。在钻头侧向力、钻头偏转角、钻头合力角、邻井造斜率以及初始井斜5个因素中，根据本文相关性分析结果，钻头偏转角对实际造斜率影响相对较小，可不予考虑；对于一口确定的井来说，邻井造斜率及初始井斜皆为常量，可根据现场数据给出；钻头侧向力和钻头合力角可根据底部钻具组合的力学特性[23-25]求出。本文主要研究造斜率预测模型精度的提升，对于力学参数的计算不展开讨论。

高精度Kriging代理模型实际使用流程如图7所示。钻井作业时，在造斜率预测系统中可提前输入邻井造斜率及初始井斜，并实时计算钻头侧向力、钻头合力角以及目标地层所需的造斜率(命名为计算造斜率)。用本文造斜率预测模型实时预测下一时刻的造斜率(命名为预测造斜率)，并与计算造斜率比较。以指向式导向工具为例，若预测造斜率小于计算造斜率，则需调节偏心环使其能够提供更大的偏置力以增加工具的实际造斜率；若预测造斜率大于工具计算造斜率，则反之。预测模型的精度越高，工具准确钻入目标地层的概率也就越大，在一定程度上能够降低井眼轨迹偏离目标地层的风险。