旋转对称二次曲面平凸透镜牛顿环研究
2023-10-17徐海斌穆成富
徐海斌,穆成富
(湖州师范学院 理学院,浙江 湖州 313000)
0 引 言
牛顿环实验是大学物理实验中的一个重要内容,也是教学研究人员的重要研究对象,因此在实验测量及数据处理[1-2]、干涉仿真模拟[3]、教学[4-5]、测量[6-8]、广义牛顿环结构[9]等领域,都被进行了广泛而深入的研究.
在理论教学和实验研究过程中,通常认为形成牛顿环的平凸透镜是由一个平面和一个球面组成的,因此已有研究通常仅考虑凸面为球面的情况.近年来,随着成像光学、照明光学及光束整形等领域的发展,光学非球面被深入研究并广泛应用于光学系统[10-13].球面是旋转对称二次曲面的一种特殊情况,因此讨论具有旋转对称二次曲面的非球面结构具有更加普遍的意义,是对现有球面结构牛顿环的有益拓展.本研究旨在对一般情况下的旋转对称二次曲面平凸透镜牛顿环进行理论分析和仿真研究,给出描述其牛顿环的数学表达式和光强分布曲线.
1 旋转对称二次曲面平凸透镜
1.1 旋转对称二次曲面
旋转对称二次曲面包括最常见的球面、抛物面、椭球面和双曲面,其标准面面形公式为[14]:
(1)

对旋转对称二次曲面,可通过其对称轴的截面进行描述.本文所采用的旋转对称二次曲面均以z轴为旋转对称轴,取xoz平面作为观察面.对于椭圆,a、b分别为长、短轴;对于双曲线,a、b分别为实、虚轴;对于抛物线,公式(1)可简化为y2=2Rz.因此,旋转对称二次曲面的结构参数可用顶点曲率半径R和conic系数k来表示,且在某种意义上,k反映曲面的平坦度.
1.2 旋转对称二次曲面平凸透镜的牛顿环
旋转对称二次曲面在xoz平面内可表示为:
(2)
旋转对称二次曲面平凸透镜关于z轴旋转对称,因此在分析xoy平面光强分布时,只需考虑其在xoz平面的截面图(图1)即可.

图1 旋转对称二次曲面平凸透镜在xoz平面的截面图
考虑入射光在基底上的半波损失,光程差为:
(3)
经过曲面和基底反射光的相干强度可表述为:
(4)
第N级暗纹满足条件:
2nzN=Nλ.
(5)
第N级亮纹满足条件:
(6)

(7)

(8)
曲面以z轴旋转对称,可取第N级暗纹或亮纹的直径DN=2|xN|,则第N级暗纹直径的平方可写成:
(9)
第N级亮纹直径的平方可写成:
(10)
式(9)和式(10)描述了一般旋转对称二次曲面产生的N级暗纹和亮纹直径.
1.3 牛顿环位置与conic系数的关系
式(7)给出了N级暗环所在位置与二次曲面顶点曲率半径、波长、间隙折射率和conic系数k之间的关系.对式(7)进行分析可知,当满足关系式(11)时,式(7)和式(9)即简化为大学物理实验中的第N级平凸透镜牛顿环暗环所在位置及其直径,即表达式(12)和(13):
(11)
(12)
(13)
化简式(11),得:
(14)
为研究各种二次旋转对称曲面平凸透镜的牛顿环位置与conic系数k之间的关系,本文取曲面顶点曲率半径R为1 m,波长λ为589.3 nm,空气间隙折射率n为1,以暗环位置为例,对各种k值下牛顿环的特征进行研究.
取牛顿环级数N为10,通过上述参数对式(14)进行分析可知,当k106时,所有的二次旋转对称曲面平凸透镜基本都能满足大学光学实验中的牛顿环公式;当k接近或大于106时,牛顿环位置和直径将会发生明显变化.
2 各种conic系数旋转对称二次曲面平凸透镜的牛顿环光强曲线
2.1 旋转对称二次曲面与conic系数的关系
根据以上参数对式(14)进行分析可知,只有当|k|接近或大于106时,近中心区域各级牛顿环的位置才会发生明显的变化.因此,首先要了解二次旋转对称曲面与系数k之间的关系.图2给出了当顶点曲率半径为1 m时,各种k值下曲面在xoz平面的曲线图形.为比较具有相同顶点曲率半径二次旋转对称曲面平坦度随k系数的变化关系,取不同的k值,并以不同的x轴和z轴为坐标轴,分别用图2的(a)(b)(c)进行描述.由图2可知,k反映了曲面的平坦程度,当k值减小时,曲面变得越来越平坦;当k值增大时,曲面变得越来越陡峭.从图2(c)可以看出,当k值为106时,曲线在x轴上的取值范围也变得很小.


图2 不同k值下旋转二次曲面在xoz平面的截面图
2.2 旋转对称二次曲面平凸透镜牛顿环强度分布与conic系数的关系
为便于对各种旋转对称二次曲面平凸透镜的牛顿环进行比较分析,取波长为589.3 nm的钠黄光作为光源,光强I0=1,二次旋转曲面的顶点曲率半径为1 m,k值的取值范围为[-106,106],利用Matlab对光强分布进行数值模拟,得到x轴方向光强分布曲线图,见图3的(a)(b)(c).
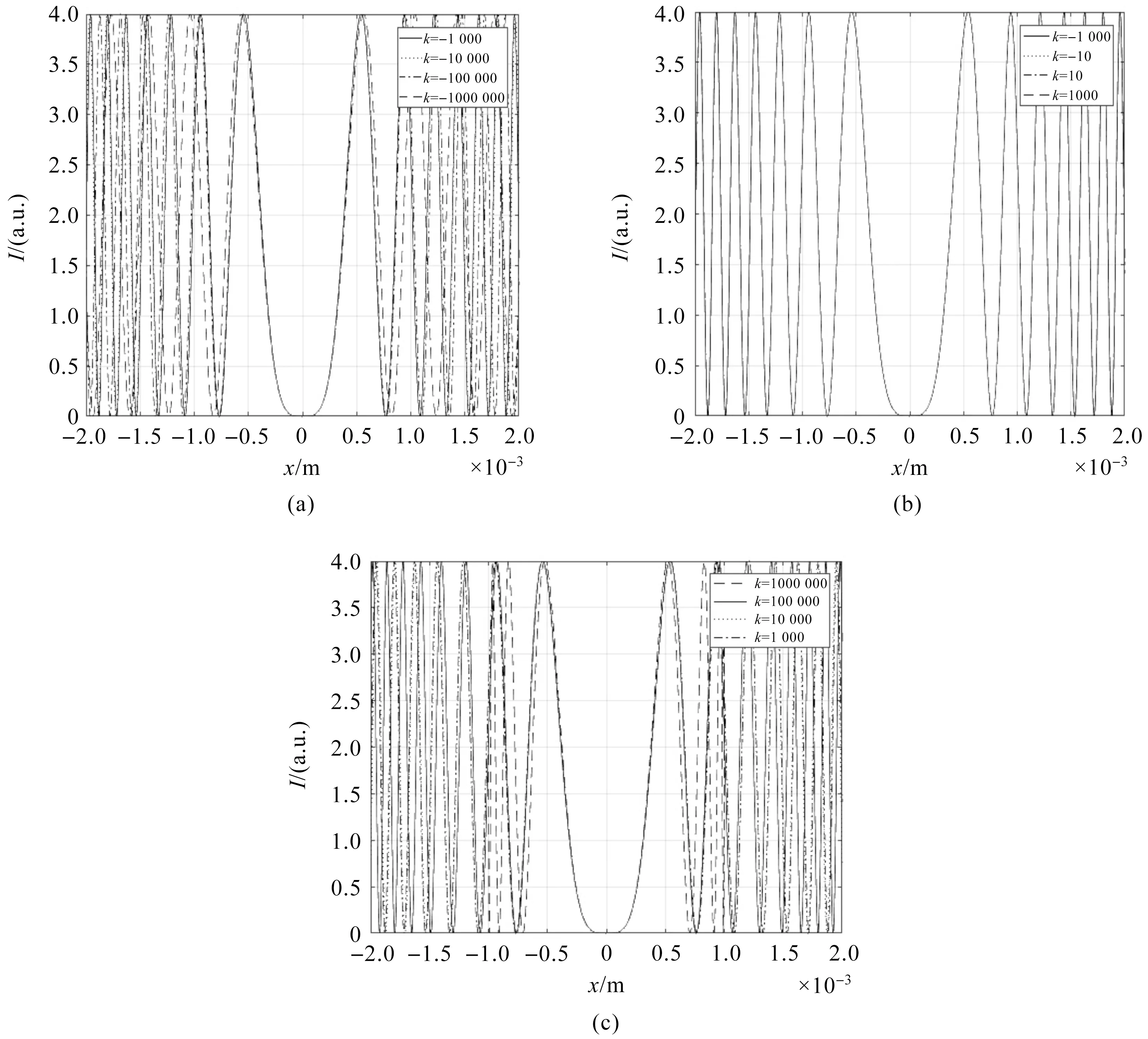
图3 不同k值下牛顿环光强随x轴的变化曲线
图3(a)给出了k值为-103、-104、-105、-106时中心区域沿x轴的光强分布曲线.从图3(a)可以看出,在中心区域,当k值为-106时,光强分布曲线明显偏离其他k值的光强分布曲线.而事实上,图3(a)只给出了中心区域的曲线变化,当x更大时,k值为-105的光强分布曲线也会明显偏离-103的光强分布曲线.
图3(b)给出了k值为-103、-10、10、103时中心区域沿x轴的光强分布曲线.从图3(b)可以看出,当k值范围为[-103,103]时,光强分布曲线基本不发生明显变化,甚至在x轴稍大的区域,光强分布曲线也不发生明显变化.由于当显示较大区域时,光线会更加紧密,因此x轴稍大的区域不在此显示.
图3(c)给出了k值为103、104、105、106时中心区域沿x轴的光强分布曲线.从图3(c)可以看出,在中心区域,当k值为106时,光强分布曲线明显偏离其他k值的光强分布曲线.研究显示,当x轴区域取更大时,k值为105的光强分布曲线相对k值为103的光强分布曲线也会发生较明显的偏移.
对图3中各种k值下的光强分布曲线进行比较分析可知,在x轴中心区域(xoy的原点附近),当k值大约在[-104,104]范围内时,光强分布曲线不发生明显变化;当k值明显小于-104或大于104时,光强分布曲线将会发生明显变化.该仿真结果与理论研究结果一致.
3 结 论
本文采用旋转对称二次曲面的标准面面形公式,对旋转对称二次曲面平凸透镜产生的牛顿环进行了理论分析和数值仿真研究,并给出了牛顿环光强分布的一般数学表达式和光强分布曲线.给定曲面顶点曲率半径为1 m,光波长为589.3 nm,当曲面的conic系数k大约在[-104,104]范围内时,完全可以像光学教材中所述,将曲面看成是球面,利用已有牛顿环的近似表达式对曲面顶点曲率半径进行研究;当k明显小于-104或大于104时,则光学教材中关于平凸透镜的牛顿环近似表达式将不再适用.该研究拓展了大学物理牛顿环实验的研究内容,能够加深学生对牛顿环实验的理解,也能为旋转对称二次非球面结构的设计、测量和调整等提供有益的参考.
