多重调和级数模的同余式
2023-10-17杨以宁杨鹏
高师理科学刊 2023年9期
杨以宁,杨鹏
杨以宁,杨鹏
(辽宁科技大学 理学院,辽宁 鞍山 114051)
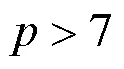
多重调和级数;伯努利数;同余式
1 引言及预备知识

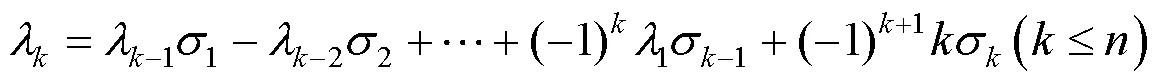
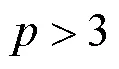
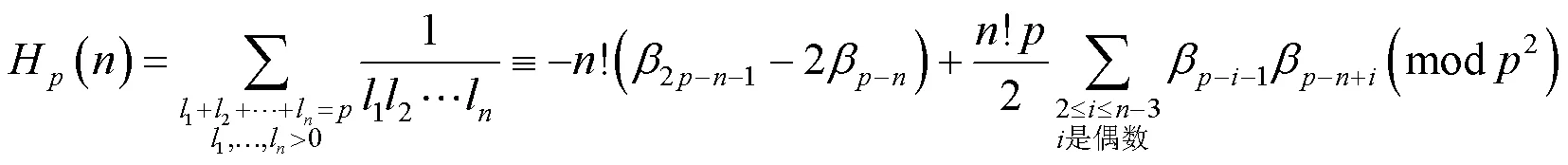
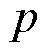
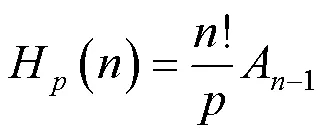
由引理2~3容易得到引理4.
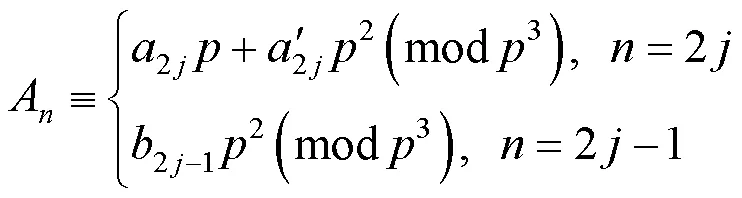
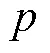
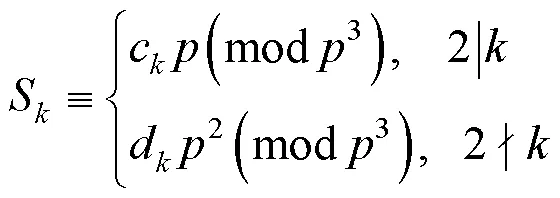

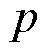

2 主要结果及证明
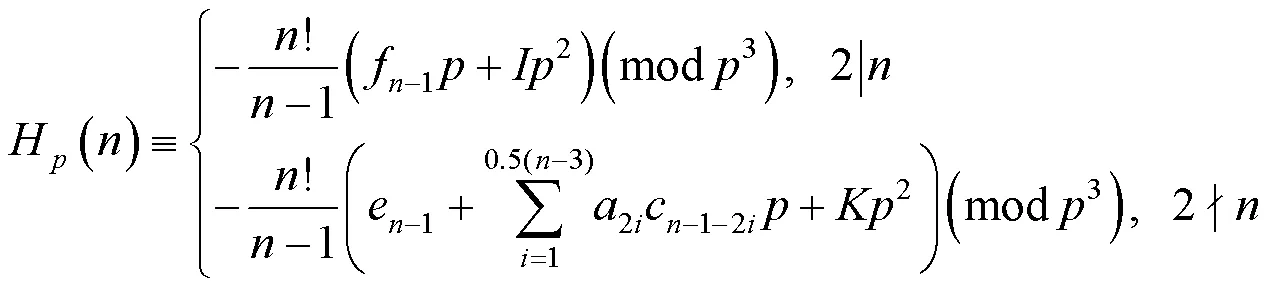
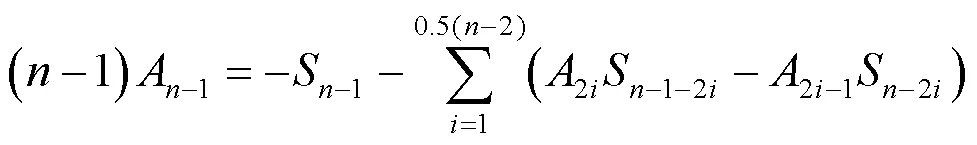
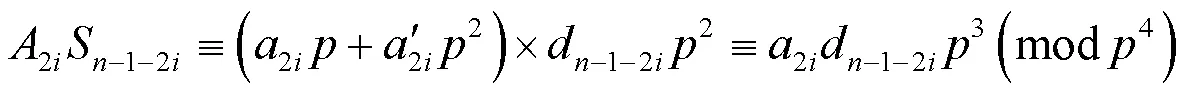

由引理5可知
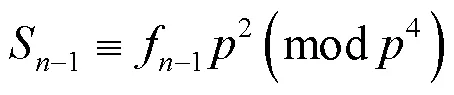
将式(10)~(12)代入式(9)中,可得.故由引理3及引理6可知
2023-10-17杨以宁杨鹏
杨以宁,杨鹏
杨以宁,杨鹏
(辽宁科技大学 理学院,辽宁 鞍山 114051)
多重调和级数;伯努利数;同余式

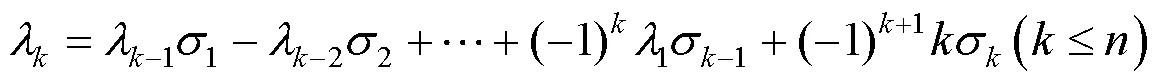
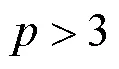
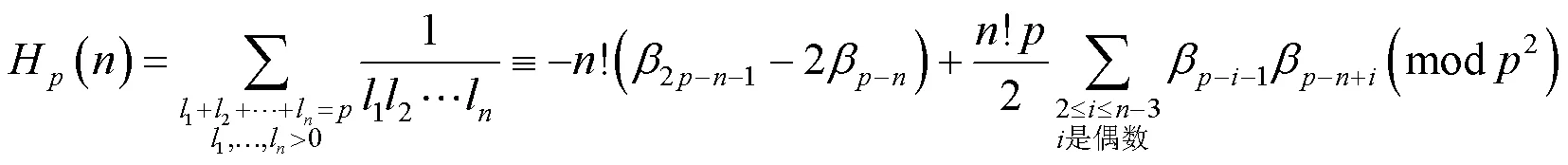
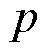
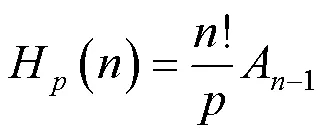
由引理2~3容易得到引理4.
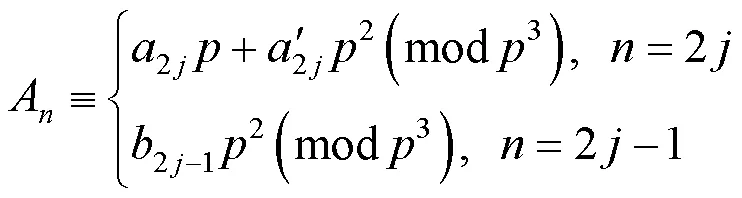
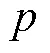
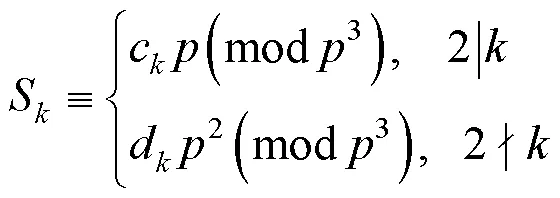

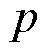

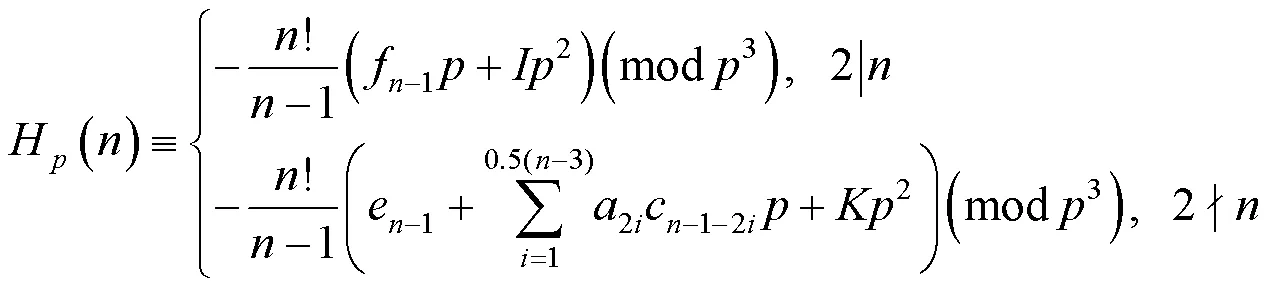
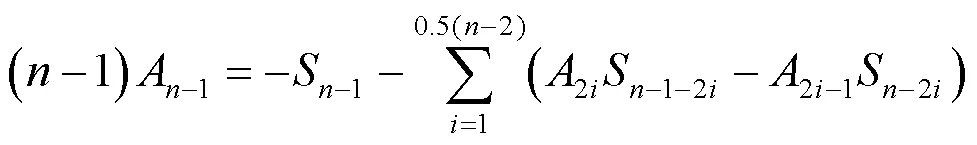
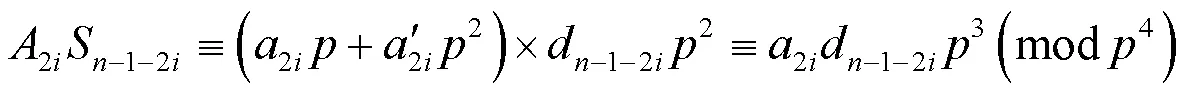

由引理5可知
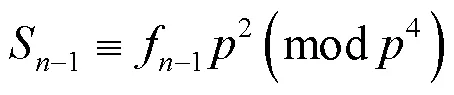
将式(10)~(12)代入式(9)中,可得.故由引理3及引理6可知