信道缩短和基于编码信道缩短
2023-10-16彭鼎祥
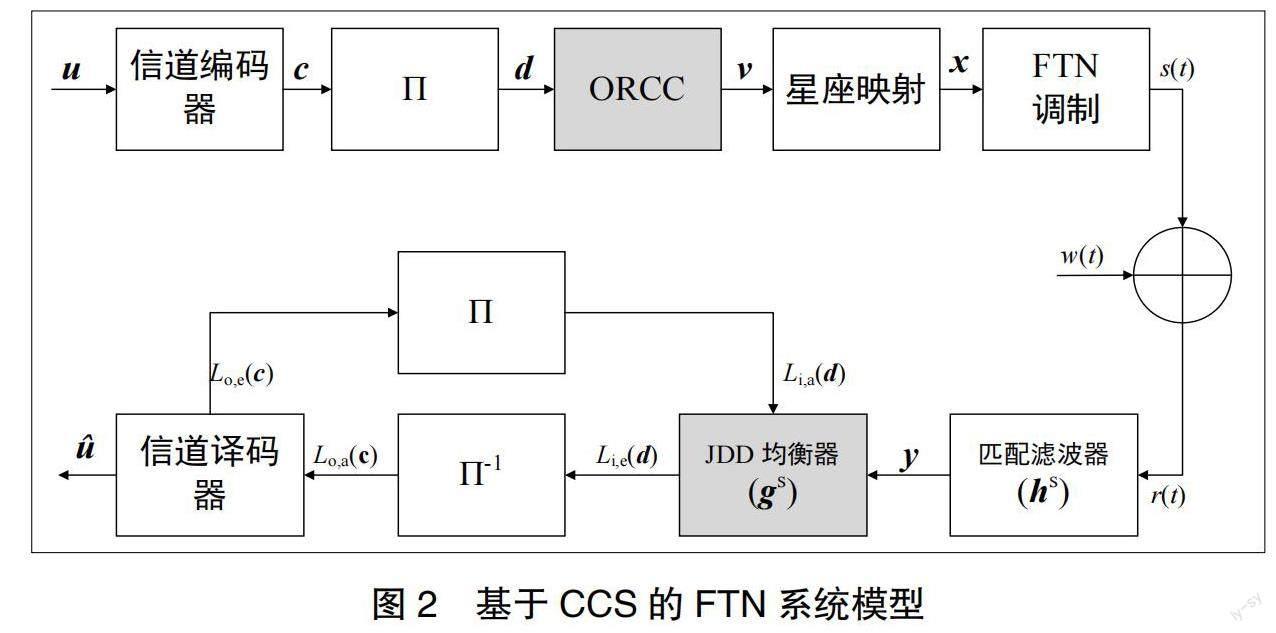
摘要:本文对比研究了信道缩短(Channel Shortening, CS)和基于编码信道缩短(Code based Channel Shortening, CCS)两种方法,发现它们在转移概率函数上具有不同的特点。通过比较符号间干扰信道的最小欧式距离(Minimum Euclidean Distance , MED)和可达信息速率(Achievable Information Rate, AIR),,找到了超奈奎斯特(Faster-Than-Nyquist, FTN)系统的可靠性能指标。在优化步骤方面,FTN-CCS先优化外码再优化内码,而FTN-CS先优化内码再优化外码。在保持相同频谱效率(Spectrum Efficiency, SE)的条件下,比较了基于CS和CCS的FTN的AIR和BER性能。研究发现,在均衡复杂度相同或更低的情况下,FTN-CS比FTN-CCS具有更好的性能。
关键词:信道缩短;编码信道缩短;超奈奎斯特;欧式距离;可达信息速率
到2025年,全球将有三分之一的人口使用5G网络。然而,随着虚拟/增强现实、自动驾驶、物联网和无线回传等新应用的兴起,人们需要比5G网络更高的数据速率[1]。为了提高频谱效率(Spectrum Efficiency,SE),超奈奎斯特(Faster-Than-Nyquist,FTN)将压缩相邻成型脉冲的传输间隔。然而,FTN传输违背了奈奎斯特定理,会造成符号间干扰(Inter-Symbol Interference,ISI)。由于严重的ISI会导致高复杂性传输,所以传统的FTN传输方法没有被广泛使用。
对于FTN传输,基于最大后验概率(Maximum Posterior Probability,MAP)准则的时域均衡复杂度为O(ψL),其中ψ表示星座图的星座点数,L表示ISI长度。当FTN的ISI长度很大时,传统BCJR均衡算法将由于高复杂度失去实用性。为了降低均衡复杂度,线性预均衡(Linear Pre-Equalization,LPE)[2]方法将FTN传输等效为Nyquist正交传输。但是当压缩因子τ<1/(1+β)时,其中β表示根升余弦(Root Raised-Cosine,RRC)的滚降因子,LPE方法将失效。为了降低复杂度[3],提出了基于最小均方误差(Minimum Mean Square Error,MMSE)准则的频域均衡(Frequency-Domain Equalization,FDE)方法。尽管MMSE是次优准则[4],但FDE无法可靠检测到高速FTN,而时域均衡在这方面则表现良好[5]。
信道缩短(Channel Shortening,CS)方法通过减小时域均衡的ISI长度L降低MAP均衡的复杂度。Falconer和Magee在文献[6]中提出了CS方法,文献[7]则对一般线性信道进行了改进。为了进一步降低均衡复杂度,文献[8]提出了基于编码的信道缩短(Code based Channel Shortening,CCS)方法。然而,缩短CS或CCS的ISI长度可能会带来性能损失,因此需要在复杂度和性能之间进行权衡。为了优化CS方法的ISI长度,可采用可达信息速率(Achievable Information Rate,AIR)接近真实信息速率的下限准则,以在不损失性能的情况下最小化ISI长度[9]。而[8]中CCS的ISI长度是基于最小欧式距离(Minimum Euclidean Distance,MED)度量进行优化的。本文旨在比较相同频谱效率(Spectrum Efficiency,SE)条件下,基于CS和CCS的FTN系统的性能和复杂度。
一、系统模型
如图1所示,基于CS的FTN发射机(FTN-CS)[7]可看作两级的串行级联码(Serially Concatenated Code,SCC)。如图2所示,基于CCS的FTN发射机(FTN-CCS)[8]可看作为三级级联的SCC。图中的灰色部分显示FTN-CS和FTN-CCS的差异。FTN发射信号可表示为:
其中Ts=τT,τ为压缩因子,是信号星座映射后的输出序列,h(t)是T正交RRC成型脉冲。 星座映射使用与文献[8]相同的BPSK调制。成型脉冲h(t)进行±ζT的截断,ζ=15[8]。
接收信号为r(t)=s(t)+w(t),其中w(t)是单边功率谱密度为N0的高斯白噪声。在FTN均衡器之前,CS方法改造了整体信道响应g={gl},其中,而CCS方法不改变整体信道响应g。
对于FTN-CS,前端滤波器hr取代了传统 FTN系统的匹配滤波器。在时域,hr将ISI能量集中以减少ISI长度。FTN均衡器將目标响应 (gr)作为ISI信道并使用BCJR算法来处理ISI。gr为辅助通道,即均衡器实际使用的信道。hr的频率响应文献[10]。
其中是gr的频率响应,Γk=|Hk|2+N0,[H0,...,HNF-1]= FFT(h),h={hk},hk=h(kTs),表示匹配滤波器的频率响应。
对于FTN-CCS,CCS均衡器使用联合检测与译码(Joint Detection and Decoding,JDD)来处理ISI。 截断响应(gs)则是FTN-CCS的辅助通道。输出保留了卷积码(Output-Retainable Convolutional Code,ORCC),它具有M个序列输入和N个序列输出。ORCC通过提供编码增益来降低均衡复杂度而不是补偿截断损失。FTN-CCS的三级SCC编码结构需要两级Turbo迭代,即FTN均衡器和ORCC译码器之间的Turbo迭代(TI1),以及ORCC译码器和信道解码器之间的Turbo迭代(TI2)。通常使用TI1代替最佳JDD,并结合由FTN和ORCC构建的超级网格来降低复杂性。TI1和TI2联合可以达到最优JDD的性能。ORCC当前输出是ORCC的网格状态的一部分和FTN均衡器下一次的网格状态的一部分。因此,超级网格可折叠为ORCC的编码网格。基于折叠网格的JDD复杂度较低,可取代了文献[8]中的TI1。ORCC有两种类型,完全可保留卷积码(FRCC)和部分可保留卷积码(Partially-Retainable Convolutional Codes,PRCC)。FTN-CCS使用PRCC代替FRCC来降低复杂性[8]。超级网格不等同于PRCC的编码网格,因为PRCC的每个编码网格状态只能提供一些在当前时间对ISI有贡献的先前符号。
二、方法比较
(一)CS和CCS的分支度量
FTN-CS的分支度量为
其中yk是hr的输出,目标响应 有Lr+1个抽头,Lr为ISI长度。hr和gr有给定ISI长度的解析解[7]。只要信噪比(Signal-to-Noise-Ratio,SNR)不是很高或很低 [10],无需调整CS参数。 FTN-CS的检测复杂度为,合理选择Lr可降低复杂性而不显著降低性能。
为了便于说明,假设N=1,FTN-CCS[8] 的分支度量为
其中,yk是匹配滤波器的输出,是ORCC保留传输符号,LI是FTN-CCS的ISI长度,。具有超级网格的最优JDD算法具有最高复杂度(个状态,其中m是ORCC的内存长度)。最优JDD算法可用复杂度较低的FTN均衡器(个状态)和ORCC解码器(2m个状态)之间的TI1代替。超级网格折叠为ORCC的编码网格(2m个状态)。如果>2m,基于PRCC的FTN-CCS以性能下降为代价降低了复杂性。
CCS虽然也进行了信道截断,但它不同于CS。CCS的辅助通道是截断响应,而CS的辅助通道是目标响应gr。CCS截断不可避免地会引入信息丢失(由m决定的)。通过合理选择Lr可以降低CS截断的影响。
(二)CS和CCS的优化指标
两个指标,MED和AIR[11],可用于评估信号通过ISI信道的性能。FTN-CS可采用AIR准则来优化ISI长度即。FTN-CCS[8]使用 MED 准则优化其对应的ORCC。
首先比较较短ISI长度信道上的MED和AIR可靠性,以找到可靠的性能指标,并以此作为优化指标避免截断或辅助通道引入的损失。本文给出一个很好的例子,短长度ISI信道C1和C2如表1所示。计算原始信道MED、AIR和BER,从而找到与BER更匹配的性能度量。表1列出了基于BPSK调制的ISI信道C1和C2的MED()和对应的错误符号图样。图3显示了基于BPSK的C1和C2的AIR。图4显示了基于BPSK的C1和C2信道对应的BER(基于相同的5G-LDPC)。对于5G-LDPC,信息长度K=8000,码率r=0.5;K=8001,r=0.75;对于r=0.89,K=8099。表2列出了C1与C2相比的AIR和BER增益。
通过上面的对比可以发现,更好的AIR性能揭示了更好的BER性能。然而,较大的不一定会带来更好的BER性能。其实,AIR计算考虑了包括MED在内的欧式距离集合。AIR是渐近度量,因为其假设具有无限码长的理想FEC。
可以看出,MED不是可靠的性能指标,而AIR是可靠的性能指标。
(三)基于CS和CCS的编码调制FTN优化
编码调制(Coded Modulation,CM)FTN-CS的优化步骤如下:①根据文献[9][12]优化FTN-CS的ISI长度;②优化外码,优化后的外码与内码对应的EXIT特性[13]能更好匹配。
CM-FTN-CCS [8]的优化步骤如下:①考虑SCC的权重分布性质确定外码;②优化ORCC,使CCS均衡对应的EXIT特性与给定的外码更好匹配。尽管文献[8]基于MED优化了ORCC,但它没有将这种优化的ORCC用于CM-FTN-CCS。
可以看出,CM-FTN-CS首先優化内码(IS长度Lr)最后优化外码。但是,CM-FTN-CCS则相反。 在EXIT特性曲线相切处,迭代译码的动态特性在确定SCC的性能方面比SCC的权重谱更重要。
三、性能评估
三级结构的FTN-CCS可等效为两级结构:一方面ORCC(码率Lorcc)可看作内码的一部分,记为FTN-CS-I,等效压缩因子τe=τ/rorcc;另一方面,ORCC也可看作外码一部分,记为FTN-CS-II,等效码率,re=r×rorcc其中r是FTN-CCS的信道编码的码率。
(一)两级FTN-CCS vs. 两级FTN-CS
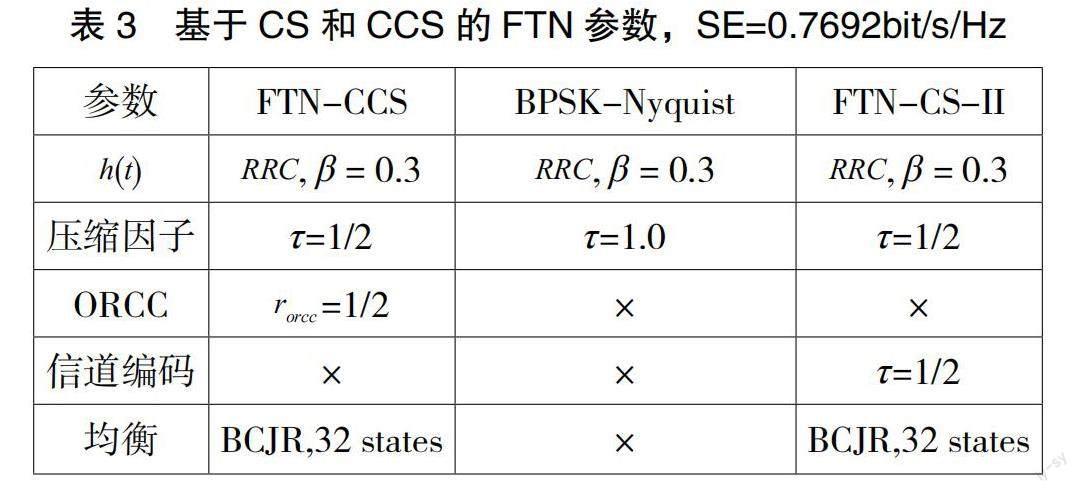
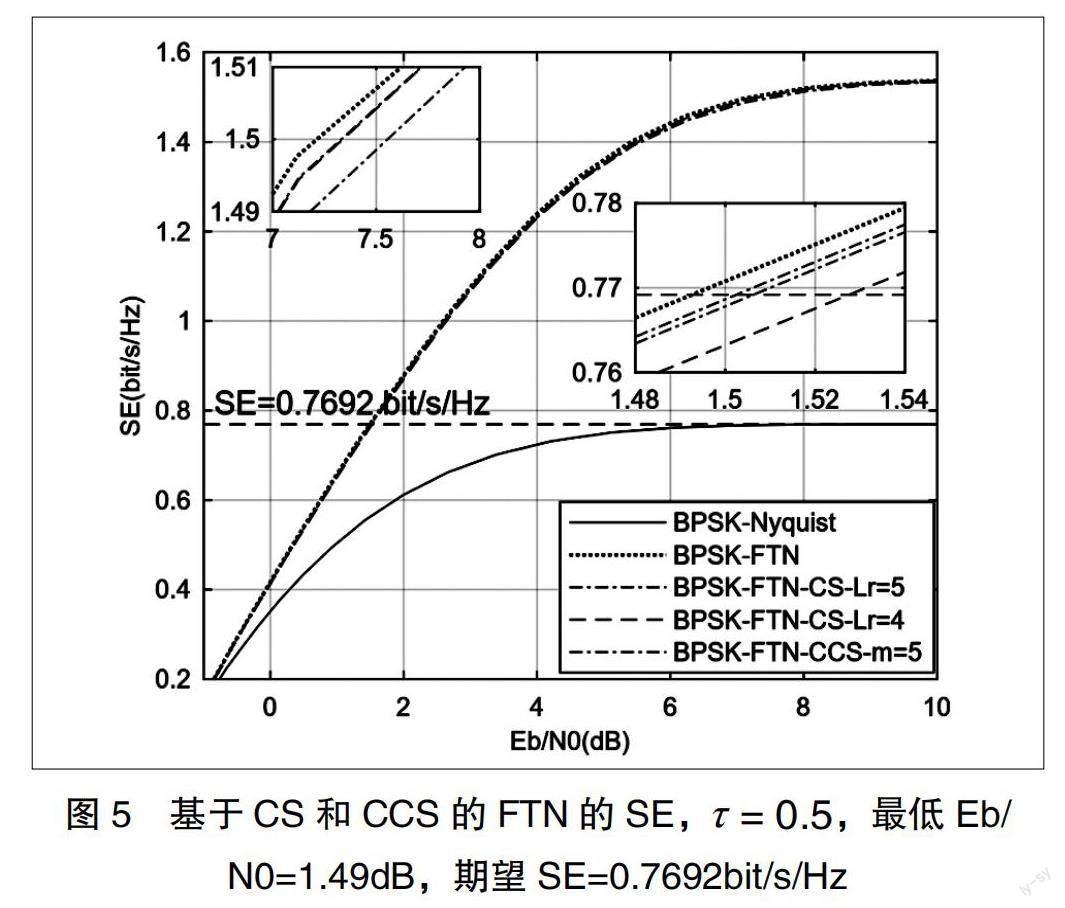
表3列出了FTN-CS-I、FTN-CS-II和FTN-CCS的参数。FTN-CCS的参数来自文献[8]中的图5。三者具有相同的SE(0.7692 bit/s/Hz)。由于τe=1.0,FTN CS-I转化为BPSK-Nyquist。图5显示了基于CS和CCS的FTN的SE。可以看出,在ISI长度相同的情况下,FTN-CS的SE性能优于FTN-CCS。对于CS,优化后的Lr=LoCpSt =4;对于CCS[8],优化后的m=5。大致相同的SE,CS的复杂度低于CCS。当SE=1.5bit/s/Hz和0.7692bit/s/Hz时,FTN-CCS和FTN-CS-I(BPSK-FTN)之间的差距分别为0.34dB和0.01dB。可以看出,对于相同的ISI长度,rorcc<1.0(M/N<1)可以减小CCS和最优SE之间的差距。
当SE=0.7692 bit/s/Hz时,图6展示了基于CS和CCS的FTN的BER性能,图中ID1代表Turbo迭代次数为1,ID5代表Turbo迭代次数为5。
FTN-CS-II采用递归卷积码(Recursive Convolutional Code,RCC)或LDPC码作为外码,FTN-CS-II-CCA采用RCC(13,15)8,FTN-CS-II-CCB采用RCC(67,117)8;FTN-CS-II-LDPC采用LDPC,最优度分布(λ2, λ3)=(0.6866,0.3134),Lr=4,m=5。当BER=10-4时,与FTN-CCS、FTN-CS-I(BPSK-Nyquist)、FTN-CS-II-CCA、FTN CS-II-CCB相比,FTN-CS-II-LDPC分别有0.9、4.7(或0.7,ID1)、5.8(或1.6,ID1)、6.1dB的增益。综上,FTN-CS比FTN-CCS具有更好的BER性能和更低的均衡复杂度。
(二)三級FTN-CCS与两级FTN-CS
表4列出了FTN-CS-I,FTN-CS-II和FTN-CCS的参数。FTN-CCS的参数来自文献[8]中的图7。三者具有相同的SE(0.5128bit/s/Hz)。图7显示了基于CS和CCS的FTN的SE,当τ=0.75时,BPSK-FTN(τ=0.75)是FTN的最优SE,当τ=0.75时,FTN的最低Eb=N0=0.51dB。对于FTN-CS-I(SE=0.5128bit/s/Hz),优化后的Lr=LoCpSt =2。当SE=0.5128bit/s/Hz时,具有相同ISI长度的FTN-CS(I或II)具有比FTN-CCS更好的SE性能(约0.1dB增益)。
当SE=0.5128bit/s/Hz时,图8显示了基于CS和CCS的FTN的BER性能。CM-FTN-CCS采用rate-1/2RCC(57)8作为外码[8],CM-FTN-CS采用LDPC作为外码。
FTN-CS-I采用LDPC码其最优度分布为(λ2,λ3,λ10) =(0.3871,0.2903,0.3226),FTN-CS-II采用LDPC码其最优度分布为(λ2, λ3)=(0.4,0.6),Lr=2,m=2。与FTN-CCS相比,FTN-CS-I和FTN-CS-II在BER=10-5时分别具有1.4和0.5dB的增益。在均衡复杂度相同的情况下,FTN-CS的BER性能优于FTN-CCS。
四、结束语
本文通过对FTN-CS和FTN-CCS包括系统模型、分支度量、优化度量、优化步骤、SE和BER性能的对比研究发现:CS可以改变整体信道响应(从g到gr),而CCS不会;FTN-CCS为降低复杂度需要以性能下降为代价,而FTN-CS则可以在不显著降低性能的情况下降低复杂度;MED不是可靠的性能指标,而AIR(SE)是可靠的性能指标。 综合对比分析可得,在均衡复杂度相同或更低的情况下,FTN-CS比FTN CCS具有更好的性能。
作者单位:彭鼎祥 锐捷网络股份有限公司
参 考 文 献
[1] T. S. Rappaport, Y. Xing, O. Kanhere, S. Ju, A. Madanayake, S. Mandal, A. Alkhateeb, and G. C. Trichopoulos, “Wireless communications and applications above 100 GHz: Opportunities and challenges for 6G and beyond,” IEEE Access, vol. 7, pp. 78 729–78 757, 2019.
[2] M. Jana, A. Medra, L. Lampe, and J. Mitra, “Pre-equalized faster-than-Nyquist transmission,” IEEE Transactions on Communications, vol. 65, no. 10, pp. 4406–4418, Oct 2017.
[3] S. Sugiura and L. Hanzo, “Frequency-domain-equalization-aided iterative detection of faster-than-Nyquist signaling,” IEEE Transactions on Vehicular Technology, vol. 64, no. 5, pp. 2122–2128, May 2015.
[4] H. Che, Z. Wu, and W. Kang, “Inner code optimization for high rate faster-than-Nyquist,” in 2019 IEEE Wireless Communications and Networking Conference (WCNC), April 2019, pp. 1–6.
[5] S. Li, W. Yuan, J. Yuan, B. Bai, D. Wing Kwan Ng, and L. Hanzo, “Time-domain vs. frequency-domain equalization for FTN signaling,” IEEE Transactions on Vehicular Technology, vol. 69, no. 8, pp. 9174– 9179, Aug 2020.
[6] D. D. Falconer and F. R. Magee, “Adaptive channel memory truncation for maximum likelihood sequence estimation,” The Bell System Technical Journal, vol. 52, no. 9, pp. 1541–1562, Nov 1973.
[7] F. Rusek and A. Prlja, “Optimal channel shortening for MIMO and ISI channels,” IEEE Transactions on Wireless Communications, vol. 11, no. 2, pp. 810–818, 2012.
[8] S. Li, J. Yuan, B. Bai, and N. Benvenuto, “Code-based channel shortening for faster-than-Nyquist signaling: Reduced-complexity detection and code design,” IEEE Transactions on Communications, vol. 68, no. 7, pp. 3996–4011, July 2020.
[9] H. Che and Y. Bai, “Coded modulation faster-than-Nyquist transmission with precoder and channel shortening optimization,” China Communications, vol. 18, no. 2, pp. 49–64, Feb 2021.
[10] A. Modenini, F. Rusek, and G. Colavolpe, “Optimal transmit filters for ISI channels under channel shortening detection,” IEEE Transactions on Communications, vol. 61, no. 12, pp. 4997–5005, December 2013.
[11] A. Alvarado, T. Fehenberger, B. Chen, and F. M. J. Willems, “Achievable information rates for fiber optics: Applications and computations,” Journal of Lightwave Technology, vol. 36, no. 2, pp. 424–439, Jan 2018.
[12] W. Kang, H. Che, and K. Zhu, “Precoding optimization for faster-than-Nyquist signaling with probabilistic shaping,” IEEE Transactions on Vehicular Technology, vol. 69, no. 10, pp. 11 470–11 478, Oct 2020.
[13] M. El-Hajjar and L. Hanzo, “EXIT charts for system design and analysis,” IEEE Communications Surveys Tutorials, vol. 16, no. 1, pp. 127–153, Jan 2014. [14] S. Lin and D. J. Costello, Error Control Coding, Second Edition. Prentice-Hall, Inc., 2004.
