轴向运动分数阶粘弹性梁的动力学模型及振动问题研究

殷凯琳,欧志英

(兰州理工大学理学院,兰州 730050)

0 引言

粘弹性梁理论对土木工程及阻尼技术具有重要的指导意义。粘弹性材料是在外力作用下,弹性与黏性两种变形机制同时存在的材料。材料的粘弹性性质依赖于时间、温度、负荷、加载速率及应变幅值等条件。许多固态新物质、新材料的力学特性超出了弹性范畴,使得粘弹性理论的出现与发展成为必然。粘弹性材料凭借弹性、黏性及减震等特性已逐渐应用于工程及航空航天领域。在载荷及环境影响下,其表现出随时间变化的粘弹性响应。常保平[1]在线性粘弹性范围内研究了粘弹性梁的动力特性。张建文等[2]考虑了具有介质阻尼及非线性粘弹性本构关系的梁方程,由此得到在一定的条件下所给偏微分方程等价于—常微分方程组的初值问题。Chen等[3]研究了以轴向脉冲速度运动的粘弹性光束横向振动的主要参数共振及粘弹性轴向运动梁的非线性动力学行为。艾智勇等[4]采用分数阶Merchant模型研究饱和地基的流变固结,并在此基础上探讨分数阶次与地基成层性对梁与粘弹性饱和地基共同作用的影响。

本研究着重将粘性系数引入分数阶微分方程的阶数,基于Euler-Bernoulli梁理论建立了粘弹性梁在位移应变条件下的分数阶动力学模型。相比整数阶模型,分数阶动力学方程的运用范围更广。采用同伦摄动法求解分数阶微分方程,通过数值结果分析了材料粘性系数、阻尼比及固有频率对梁模型振动的影响。

1 基础知识

近年来,分数阶微分方程(FDE)已被广泛研究并应用于诸多学科(如物理、化学、数学、工程等),其中最常见的是以下两种形式:Riemann-Liouville型定义采用微分-积分形式避免了极限求解。在粘弹性材料研究中引入Caputo型微分,现实实际问题建模过程中广泛应用Caputo型定义。

定义1:Riemann-Liouville型[5]

(1)

性质1:线性性质

(2)

此性质可通过简单的代数运算证明,并对所有其他类型的定义也成立。

性质2:由定义

(3)

交换积分次序得

(4)

定义2:Caputo型

(5)

其性质类似Riemann-Liouville型。

2 问题模型

梁理论是一个简化线性弹性理论,用于计算梁受力与变形特征,是梁得以运用于工程力学、经典梁力学的基石。梁理论基本建立了有关经典梁模型的全套理论体系,是后续一切梁分析的核心。结合梁理论考虑如图1所示的粘弹性梁模型,具有均匀轴向运动、密度ρ、截面积A、惯性矩I及初始张力P0的粘弹性梁在外部激励F(x,t)的作用下沿棱以轴向传输速度v(t)移动,棱的两端相隔距离L。仅考虑横向位移u(x,t)描述的弯曲振动,其中t是时间坐标,x是轴向坐标。

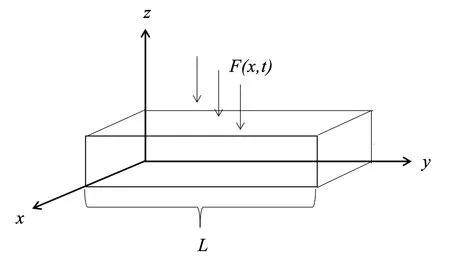
图1 轴向运动的粘弹性梁模型Fig.1 Viscoelastic beam model with axial motion

Euler-Bernoulli梁方程是一个关于工程力学、经典梁力学的重要方程,其内容描述了梁的位移与载荷的关系:

(6)

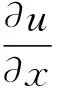
通过分析梁的动力学方程、牛顿第二定律及欧拉-伯努利假设,忽略惯性矩与剪切变形,可以得到梁的动力学控制方程。结合本构方程、动力学方程及边界条件的无量纲变换,对非线性动力学模型进行简化。假设粘弹性材料服从分数开尔文-沃特模型,故材料的本构方程[6]可以写成:

(7)

其中,φ(x,z,t)是法向应力,ω(x,z,t)是轴向应变,E0(x)是梁材料的杨氏模量,E1(x)是剪切模量,α是黏度系数。

在固体力学中,弯曲力矩是指当外力或力矩施加到结构元件上时,在结构元件中引起的反作用力导致元件弯曲。为了平衡,外力或外力产生的力矩必须由内部荷载引起耦合平衡,其中产生的内部耦合称为弯矩,因此弯矩是当外力或力矩施加到元件上时在结构元件中引起的反应,也是对应施加外力合成的内力偶分量。任何截面上的弯矩-应力关系由以下公式确定:

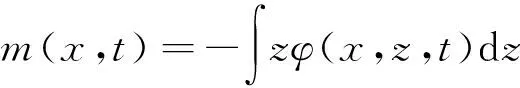
(8)

根据牛顿第二定律和欧拉-伯努利假设,忽略惯性矩与剪切变形,得到梁的动力学控制方程:

(9)

3 定解问题的求解

对于无限制的小变形效应,可以将位移关系表示为:

(10)

梁的弯矩:

(11)

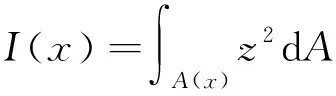
(12)

这里参数ρ、A、v、E0、I、E1、P0、φ是常量。

近年来,同伦摄动法(HPM)被广泛应用于求解分数阶微分振动、异常扩散、非线性波动、阻尼控制等问题,其主要思想是根据已知方程构造同伦函数。以下面的方程式为例:

L(u)+N(u)=f(r),r∈Ω

(13)

其中,L是线性算子,N是非线性算子,f是已知的解析函数,Ω为r所符范围。建立以下同伦格式:

H(v,p)=(1-p)[L(v)-L(u0)]+p[L(v)+N(v)-f(r)]=0

(14)

或简化为:

H(v,p)=L(v)-L(u0)+pL(u0)+p[N(v)-f(r)]=0

(15)

其中,p∈[0,1]中的是一个隐含参数。假设上述方程的解具有以下形式:

v=v0+pv1+p2v2+…

(16)

当p接近1时,可获得以下结果:

(17)

这是原方程的解。

将同伦摄动方法应用于非线性问题[7],可获得解析近似解。本研究使用一种新的改进同伦摄动方法[8]来解决问题。将方程式(12)改写为:

(18)

构造同伦函数:

(19)

根据该方程在相应载荷条件下的解,用数值结果说明基于USD控制方程粘弹性梁的响应。此处考虑简支梁,f(x)表示为:

(20)

可将其看作是单自由度理想梁的力分布,通过截断无限阶来进行数值计算。参考文献[9]中的模型,假定在USD控制方程中E1/m=2ηw3/2、w2=E0I/ρA。

这里ρA=1、L=π、m=1、v=0.2、P0=0.6、φA=0.8,其中η是阻尼比,w是固有频率。

设定条件中固有频率w=5 rad/s,阻尼比η=0.5与α=0.5,绘制梁的横向运动如图2所示。

图2 USD控制方程的单位阶跃响应Fig.2 Unit step response of USD control equation

结果表明,粘弹性梁在初始时刻先开始振荡,逐渐趋于静态平衡位置。为了比较不同分数阶α对梁振动的影响,分析了局部阶跃响应。

为了进一步验证分数阶α对USD模型中粘弹性梁振动的影响,取参数α=0.4、0.5、0.6、0.7,绘制u(x,t)随x与t变化的图像。

图3显示,当时间坐标固定,粘弹性梁沿轴向坐标的振动随着α的增加而减小。当轴向坐标固定,粘弹性梁沿时间坐标的振动随着时间增加慢慢趋于静态平衡状态,且α越小,其接近平衡的速度越快。在USD控制方程中固定分数阶的条件下,分析阻尼比与固有频率对轴向运动粘弹性梁振动的影响,展示当阻尼比不同时,粘弹性梁在USD模型下的振动变化。

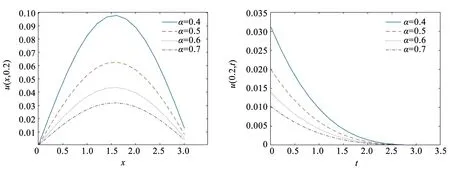
图3 USD-α对梁振动的影响Fig.3 Influence of USD-α on beam vibration

图4显示,当时间坐标固定,阻尼比越小,粘弹性梁的振动越大。当轴向坐标固定,阻尼比越小,梁的振动趋于平衡静态位置的速度越快。以下展示当固有频率w取不同值时,粘弹性梁在USD模型下的振动变化。

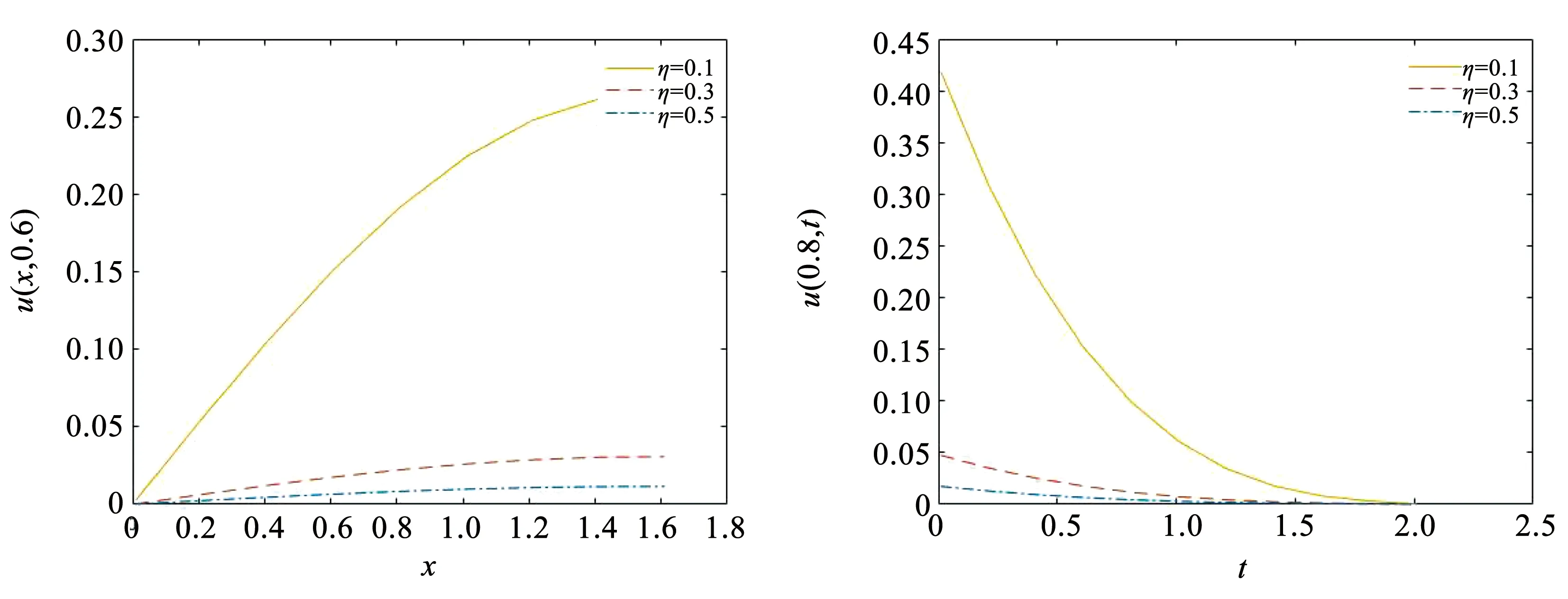
图4 USD-η对梁振动的影响Fig.4 Influence of USD-η on beam vibration

图5显示,当时间坐标固定,固有频率越大,粘弹性梁随轴向坐标变化的振动越大。当轴向坐标固定,在x=1.4前,固有频率越高,梁的振动越快趋于平衡静态位置。在x=1.4后,固有频率越低,梁的振动越快趋于平衡静态位置。根据算例分析可得到USD模型中梁振动随各参量的变化,如表1所示。

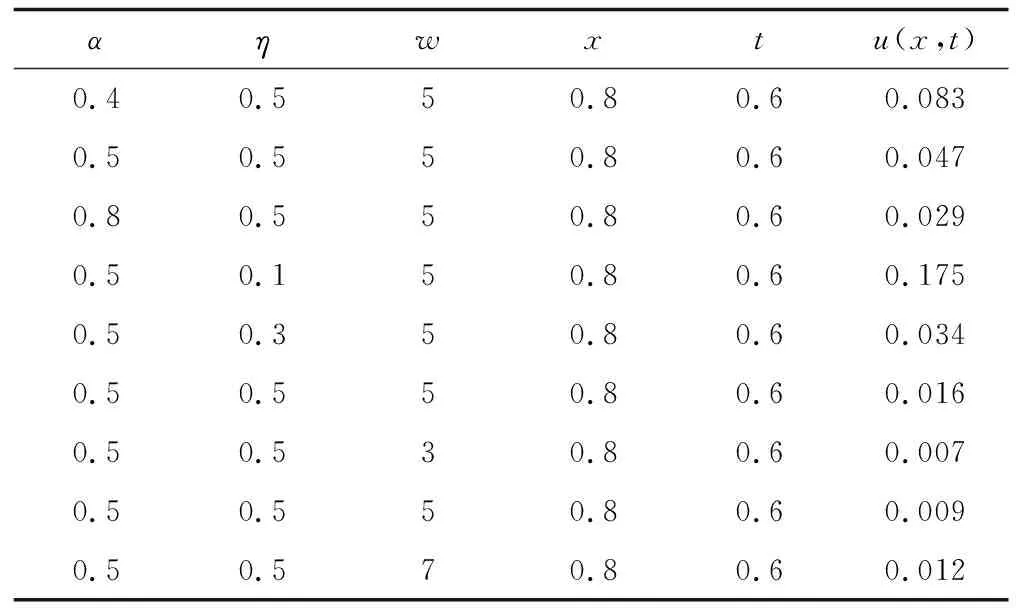
表1 各参数与USD模型的关系Tab.1 Relationship between various parameters and the USD model

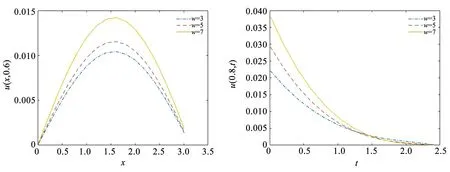
图5 USD-w对梁振动的影响Fig.5 Influence of USD-w on beam vibration

对于阶跃响应函数的作用,轴向运动的粘弹性梁经历了非常不同的过程,先在静态平衡位置附近振荡,缓慢地趋于零位移。也可以相应地对脉冲响应函数进行分析,通过改变系数值来总结结果与变量之间的关系。

4 结论

基于Euler-Bernoulli梁理论建立了分数阶型USD粘弹性梁模型,通过数值模拟对其响应进行分析。结果表明,分数阶、阻尼比及固有频率对梁的横向位移的振动有不同的影响。改进同伦摄动法可用来求解具有任意阶数的分数微分的线性微分方程,其可以描述分数阶粘弹性梁的结构,从而得到简支梁在受阶跃与脉冲两种负载情况下的无穷求和表达式的解。从数值结果比较可得出分数阶变化对USD模型影响最大,阻尼比变化及固定频率变化对模型影响较小。本研究考虑的应用模型是粘弹性梁,其方法也可参考适用于其他类型的梁模型系统。