城市道路平面几何线形优化设计研究

林庚钗

（泉州市路桥发展集团有限公司 ,福建 泉州 362000）

0 引言

日益增加的城市公路交通和安全问题往往证明，建设新的城市公路和绕行路线，或重新调整和扩建现有城市公路是合理的，因此，公路机构面临着寻找和设计最佳替代方案的挑战[1]。用现有的方法寻找优选的公路替代方案需要大量的资源，此外，各机构在调整道路和估算其成本时经常面临复杂的决策，因为该项目应基于对许多相关因素的综合分析[2-3]。采用工程判断和人工成本效益分析的结合是有效的分析方法，通过加权标准分析对备选方案进行排名，手动识别其中一组可行的备选方案，并根据总分进行排名[4]。该分数由为各种标准分配的权重组成，然后利用历史单位成本数据、工程判断和试错，对规划、设计、通行权获取、环境影响缓解和施工的总成本进行初步估算[5]。

该文采取一个简单而通用的优化问题的公式，以进行水平道路设计，通过确定问题的决策变量，将水平对齐设计框架化为约束优化问题，寻找连接两个终端的最优路径，并通过实例验证公式的有效性。

1 平面线形的数学模型

1.1 设计变量

实现给定两点a和b之间的道路设计，水平道路线形应由直线段、圆曲线和缓和曲线以适当组合形成，在给出的模型当中，这些曲线是回旋线。如果路径由N+1条切线组成，则它明确地由顶点（vi=(xi,yi),i=1,…,N）这些切线相交的位置，以及半径（Ri≥0,i=1,…,N）和角度（ωi≥0,i=1,…,N）的圆形曲线形成，如图1所示。因此，对于每一个N∈Ψ，定义XN=(x1,y1,R1,ω1,…,xN,yN,RN,ωN)∈R4N,为路线优化问题中决策变量的向量。此外，用表示由XN确定的曲线（道路路径）。

图1 连接两个终点站a和b的水平道路路线

1.2 弧长参数化法

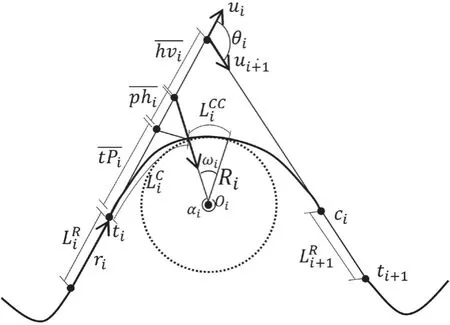
图2 水平道路线形中涉及的变量的命名约定

单位向量给出切线j的方向和意义：

切线j的方位角：

切线之间的方位差i和i+1：

圆曲线长度：

每个回旋线的长度依次如下：

在直线段i和转弯i的起点之间的交界处：

（1）圆曲线的半径和角度必须是非负的，即对于i=1,…,N，要求Ri≥0；ωi≥0。

（2）圆曲线的角度必须小于或等于每一圈相应切线之间的方位差。

（3）第i+1转弯必须在第i转弯结束后开始。

2 平面线形优化设计的一般公式

集合Cad依赖于正在处理的特定问题，并且根据它，模型定义了函数允许集。

另一方面，追求的目标是设计一条在某些技术方面最终被证明是最佳的道路路线（最大限度地减少长度、土方、征用成本、环境影响，...）,目标函数的定义和计算在任何实际应用中都是至关重要的。为了寻求对问题简单而一般的表述，引入一个函数F：Cad→R给出每条路径的成本。因此，将JN：R4N→R定义为JN(XN)=F，设计连接a和b的最佳水平道路线形的问题包括解决以下问题：

对于每个N=1,2,...，并选择与最低值对应的

数学函数F是每个特定问题的特征，在许多实际应用中，获得F（综合所有现有成本）的良好表达式可能是一项困难的任务。为了定义函数F，模型提出域Ω上的每个点都有一个价格(成本)，因此，在某种程度上，存在一个函数p(x,y)，它给出了经过的路径（x,y）∈Ω的价格。加上道路所经过的所有位置的价格，模型得到了布局的总成本，在这种情况下，考虑到函数是关于弧长参数的的参数化，目标函数JN由下式给出：

它可以通过使用合适的数值积分公式来计算。

由函数p给出的价格概念应理解为模拟各种可能性的一般函数：它可以是经济的(征用价格、沥青成本、土方工程等)，也可以是环境、生态的。这一价格也可以被视为通过某些点的惩罚，这允许通过包括布局不能与目标函数交叉的点来简化Cad。最后，p(x,y)也可以是不同类型价格的组合（加权和）。如果想要考虑所有现有的成本，获得函数p，就像函数F一样，可能是一项困难的任务。但是，在一些简单的应用中，函数p可以很容易地定义。

3 新的道路布局设计

当准备设计一条连接两个终点a,b∈R新道路的水平线形，需要满足以下限制：所有圆曲线的半径至少为50 m，直线段必须超过100 m，每个回旋线的长度至少为95 m。

关于目标函数J，模型研究以下两种不同的情况。

3.1 尽量减少长度并避开障碍物

该不连续函数p可以通过平滑近似来逼近，以保证公式（8）的平滑性，并使用可微优化算法来解决问题（7）。以下示例说明了这种方法（及其良好的性能），

寻求从点a=(0,1)开始，到达点b=(5.2,2.1)的最短路径，满足定义可接受集合的限制，并避免穿过以C1=(1,1)、C2=(2.3,2.4)、C3=(4.2,1.3)为圆心的三个圆且半径分别为R1=0.6、R2=0.9、R3=1，如图3所示。正如预期的那样，最佳解决方案是达到N=3，重点结果如表1所示。该方法的良好表现如图3所示，其中模型绘制了要绕过的障碍物，以及通过一转、两转和三转计算出的最佳道路线形（N=1；N=2且N=3）。

表1 路径规划参数计算结果

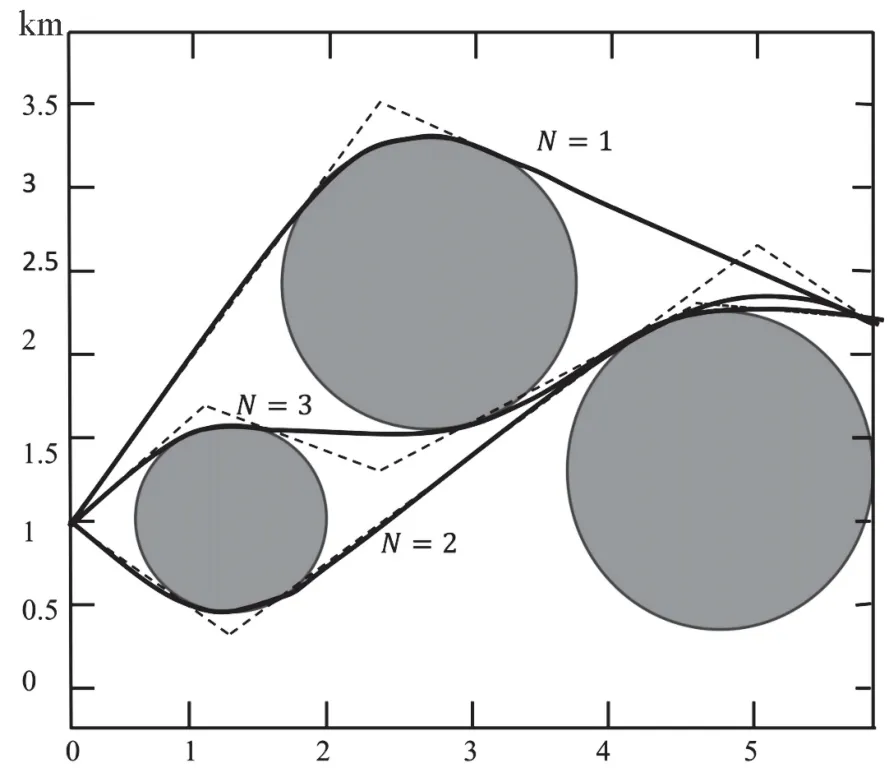
图3 路径切线和限制区域规划

3.2 最小化斜率和长度

在以上实例中，通过模型寻求使坡度最小的最短水平路线。模型设定有一个函数H(x,y)，它给出了Ω的每个点的海拔。

对于平滑的参数化曲线C={α(t)}=(α1(t),α2(t)),，每个点的斜率由下式给出：

该公式能很好地计算道路设计的最佳坡度和长度，通过实例计算得到N=3的参数效果最佳解，数值结果如表2所示。

表2 最佳坡度和长度路径规划参数计算结果

如果只允许转弯（N=1），则最佳解决方案是绕山绕行，调整路线以大致在相同的高度上行驶。这会导致巨大的圆形曲线，从“道路设计”的角度来看，这是不可取的。如果允许多转弯，最佳解决方案就是穿越山脉的布局，从而大大减少路径的长度。还可以看出，在两种情况下（N=2和N=3），布局都试图避免陡峭的斜坡，正如预期的那样，3圈对齐（N=3）是最好的解决方案。

4 案例分析

该文以一段3.5 km的道路为研究对象，该段道路在2013年经批准进行道路重建。在进行优化设计的时，由于新布局必须验证的约束，假设所有圆曲线的半径必须至少为30 m，圆曲线的长度必须在80~450 m之间，每个回旋曲线的长度必须在85~1 300 m之间，直线段必须为100~2 500 m之间。根据旧布局的一些合适点的坐标，使用三次样条插值构造目标函数，得到JN的计算结果如表3所示。

表3 案例路径规划计算结果

如表3所示，道路改进的最佳选择是三转弯（N=3），结果表明，随着转数的增加，可以获得对旧布局的更好调整。对于N=1，由于只允许一个转弯，最优解在于与旧路径中最长的直线段相交，但整体最优解还是N=3时的改进方案。

5 结论

由一系列切线、圆曲线和回旋曲线组成的水平道路线形设计是通过切线（顶点）以及圆曲线的半径和角度的交点独特地建立的。在该文中，所使用的模型能够从这些值中根据弧长参数获得布局的完整参数化。对价格的广泛解释能够解决现实中的各种问题，这种方法可以成为改善道路重建项目中路线规划的好方法，根据实例所获得的结果认可所采用的模型和计算方法是寻求新道路初始路线很好的工具。