饱和度方程一般形式的理论内涵及应用实践

2023-10-13王克文武宏亮

中国石油大学学报（自然科学版） 2023年5期

李宁, 王克文, 武宏亮, 冯周, 田瀚

(中国石油勘探开发研究院,北京 100083)

含油(气)饱和度是储集层测井定量评价的关键参数。由于油气与地层水在电性上的差异显著,故基于电性的饱和度评价一直是测井饱和度定量评价的主要方法,该方法的核心是确定电阻增大率与含水饱和度之间的关系式。除1941年Archie公式[1-2]外,国内外学者提出了一系列针对不同类型储层的饱和度模型,如层状泥质砂岩导电模型、W-S模型、D-W模型和三孔隙度模型等[3-9]。1989年李宁从非均匀各向异性地层及其等效导电模型出发,通过完整的数学推导,给出了电阻率与含水饱和度之间的一般关系式[10-11]并对其截短方式进行了论述。近年来,有研究者采用数字岩心技术开展复杂储层电性模拟研究,亦提出针对不同类型储层的饱和度计算公式[12-13];也有一些研究者分析或综述了不同类型储层饱和度模型、岩电参数的研究现状及进展[14-17]。这些研究与综述为认识复杂储层电性规律、分析确定测井饱和度评价模型发挥了重要作用。然而深入分析发现,不同学者关于测井饱和度评价模型的研究多针对某些特定储层类型进行,而很少涉及对储层饱和度模型普遍规律的探讨。笔者首次将电阻增大率-含油(气)饱和度方程一般形式的不同截短方式形成的矩阵视为一种“周期表”,研究其变化规律及理论内涵,并通过实例展示在复杂储层饱和度模型确定中的实际应用。

1 饱和度方程一般形式及其截短方式的周期变化规律

李宁[10]从非均匀各向异性地层及等效导电模型(图1)出发,通过完整的数学推导,给出了电阻增大率与含水饱和度之间的一般关系式,并证明常用的Archie方程、W-S方程和D-W方程等均为该一般形式的特例[10-11]。

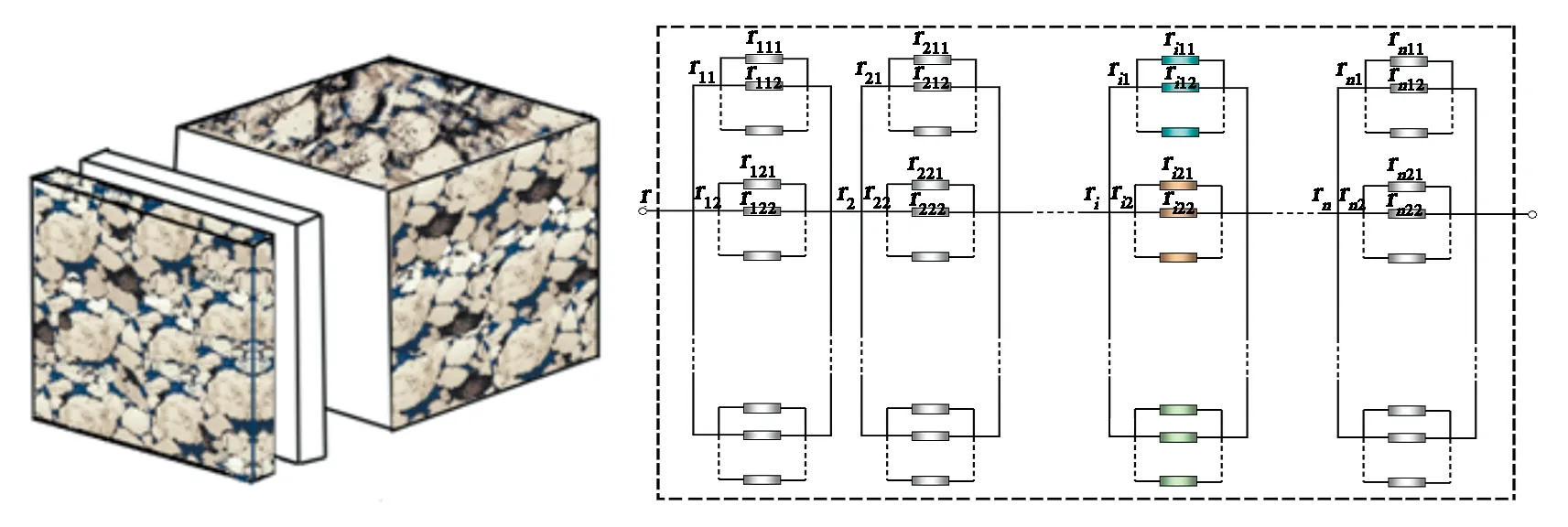
图1 非均匀各向异性地层及其等效导电模型

李宁导出的电阻增大率与含水饱和度的一般形式为

(1)

式中,I为电阻增大率;Sw为含水饱和度;pi、hik和θik为待定参数。

式(1)给出了非均质复杂储层电阻率与含水饱和度关系的一般表达式,由于含油(气)饱和度等于1减含水饱和度,所以上式也即电阻率与含油(气)饱和度的一般形式。在实际应用中需针对具体情况本着适度、够用的原则截取一般形式满足精度要求的最短形式,也称为最佳形式。这一过程类似泰勒级数逼近,根据不同精度要求依次保留泰勒级数中的一次、二次或多次项。

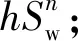
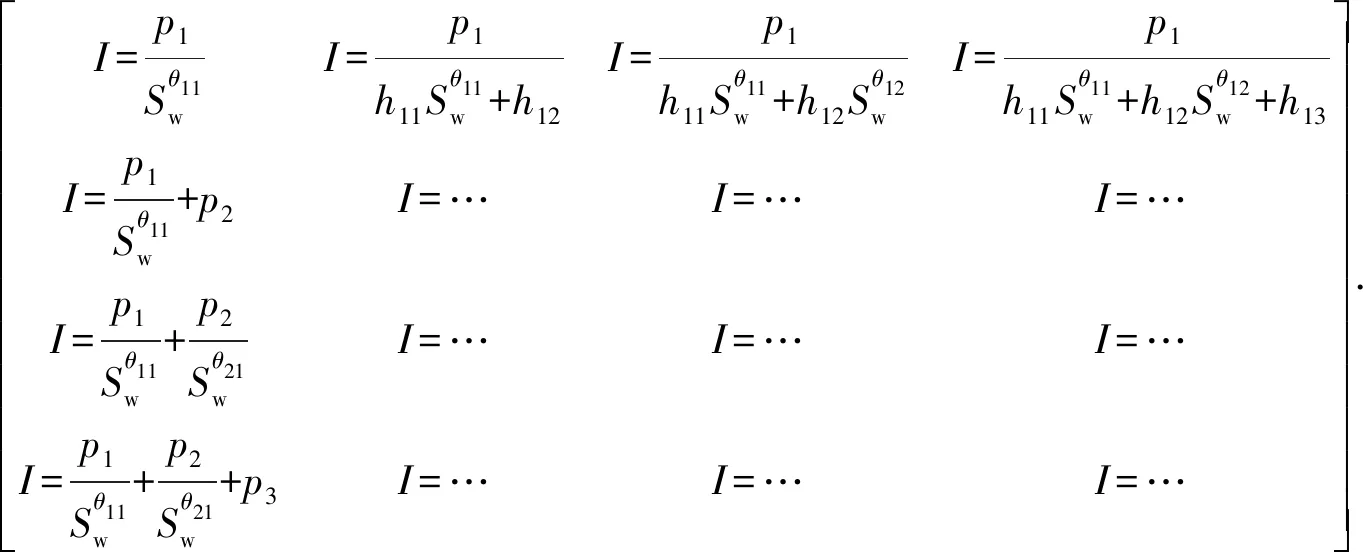
(2)

2 常见饱和度模型在周期表中的位置

饱和度模型周期表给出了影响因素从单一到复杂不同情况下饱和度模型的结构特征,常见饱和度计算模型均与周期表特定位置的截短形式对应。

2.1 纯砂岩储层

1941年Archie通过对实验室条件下各种砂岩饱含盐水电阻率测量结果分析,提出了电阻率增大率与含水饱和度之间的关系,即Archie公式:

(3)

式中,n为饱和度指数。式(3)适用于均匀各向同性纯地层饱和度计算。当周期表式(2)左上角公式中参数p1取值为1时即为Archie公式(式(3))。

2.2 泥质砂岩储层

Poupon等[3]提出层状泥质砂岩导电模型,该模型认为泥岩和砂岩薄层的电导率是严格相加的,而且泥质的附加导电性与含水饱和度无关。根据电阻增大率的定义及Poupon等的假设,其饱和度模型的形式为

(4)

式中,分母中第1项代表传统Archie公式;常数h2体现了泥质的附加导电性,且与含水饱和度无关。式(4)与周期表中第1行第2列的截短形式对应。

Waxman和Smits[7]在Hill和Winsauer的研究基础之上提出考虑黏土阳离子交换能力的W-S模型。根据电阻增大率的定义,基于泥质阳离子交换导电的W-S,泥质砂岩饱和度计算模型可以化为

(5)

式中,分母中第1项代表传统Archie公式,而第2项代表泥质对电性的影响。式(5)与式(4)的差异在于泥质对电性的影响是否与含水饱和度有关,该差异同时也体现了泥质砂岩体积模型与阳离子交换模型在刻画泥质导电性上的不同。式(5)与周期表中第1行第3列的截短形式对应。

2.3 孔洞型火山岩、碳酸盐岩储层

溶蚀孔洞是火山岩、碳酸盐岩储层常见的孔隙类型,孔洞对电性的影响与孔洞的连通特性有关。当孔洞未被裂缝连通呈孤立状存在时,其对电性的影响表现为串联特性。李宁等[18]通过试验研究了大庆深层火山岩储层的电阻率特征,测量样品来自5口深层气井的9块全直径岩样。对岩心电阻率试验数据定量分析表明,I-Sw关系存在以下2种形式:

(6)

(7)

式(6)、(7)不仅对火山岩储层适用,也适用于孔洞型碳酸盐岩储层。式(6)、(7)分别与周期表中第1列第2行、第1列第3行所在位置的饱和度截短形式具有相同的结构,其差异与孔洞在储层中分布及其连通特性有关。

3 饱和度模型截短形式周期变化的理论内涵

研究表明,对于同一组岩电试验数据,有可能存在不同的饱和度截短形式同时达到理想的拟合精度,这说明考虑模型的物理意义比单纯考虑拟合精度更为重要。因此有必要开展饱和度模型截短方式矩阵周期变化理论内涵的探讨。

储层岩石是一种典型的多孔介质,所有影响骨架或孔隙流体导电性的因素均对储层岩石宏观电性具有影响,如导电矿物、泥质类型与含量、润湿性、矿化度、孔隙类型与结构特征等均对岩石电性具有影响。尽管不同因素对储层岩石电性影响的微观机制存在差异,但某因素对宏观电性的影响总可以抽象为并联、串联或者串并联结合。

关于岩石电性的影响因素及规律,目前的研究普遍认为:水湿储层电阻率指数低的原因在于水湿储层岩石表面存在润湿水膜,该水膜为电流提供了与孔隙流体并联的电流通道,因此润湿水膜对储层岩石电性的影响表现为并联特性[19];无论是等效体积模型还是阳离子交换模型,泥质对岩石电性的影响表现为“附加导电”,即呈现并联导电特性[3-6];当岩石骨架中含有磁铁矿、黄铁矿等导电矿物时,除孔隙水导电外,还存在骨架附加导电[20]。

孔隙结构对储层岩石电性的影响规律比较复杂,因此孔隙结构定量描述及对岩石电阻率的影响规律一直是国内外研究的重点。根据形成地质背景的不同,孔隙可以分为基质、次生孔洞和裂缝等不同孔隙类型。不同类型孔隙的尺寸、形状及空间连通性不同,对岩石电性的影响存在很大差异。理论及试验研究表明,孤立孔洞对电性的影响呈现串联特性,而裂缝对电性的影响呈现并联特性[15,21]。

假设储层中存在2种不同的孔隙系统,其孔隙度分别为φ1和φ2,且每个孔隙系统均满足Archie公式,则饱含水时2个孔隙系统的电阻率分别为

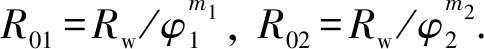
(8)

式中,Rw为地层水电阻率,Ω·m;R01和R02分别为2个孔隙系统饱含水时的电阻率,Ω·m;m1和m2分别为2个孔隙系统的胶结指数。

含油(气)时2个孔隙系统的电阻率为

(9)

式中,Rt1和Rt2分别为2个孔隙系统含油(气)时的电阻率,Ω·m;n1和n2分别为对应的饱和度指数。

若2个孔隙系统的导电特性呈现并联特性,由式(8)、(9)可以得到储层岩石电阻增大率I的表达式为

(10)

式中,p1和p2为待定常数,且满足p1+p2= 1。

同理,若2个孔隙系统的导电特性呈现串联特性,则由式(8)、(9)可以得到储层岩石电阻增大率I的表达式为

(11)

式中,p1和p2为待定常数,同样满足p1+p2=1。

仔细分析式(10)、(11),并结合前面对常见饱和度模型在周期表中的分布规律分析,可以得到以下3点认识:

(1)当某影响因素对电性影响呈现并联特性时,饱和度模型的形式为在原模型分母上增加一项;当某影响因素对电性影响呈现串联特性时,饱和度模型的形式为在原模型右端增加一项。

(2)增加项的具体形式与影响因素本身特性有关。若某因素对电性的影响是恒定的则为常数,否则为非常数项。

采用溶剂挥发法制备Lut-SD。取圆底烧瓶，称取一定量的Lut和载体材料，加入无水乙醇。于45 ℃水浴条件下持续搅拌至溶液体系变澄清。减压旋蒸除去无水乙醇有机溶剂，固体物于45 ℃真空干燥箱中过夜干燥，即得Lut-SD，并于干燥器中敞口保存。

(3)若某一影响因素对储层岩石电性的影响呈现并联特性,其饱和度模型最优截短形式沿周期表的横向作规律性变化,如泥质砂岩、含裂缝储层饱和度计算模型等;若对储层岩石电性的影响呈现串联导电特性,其饱和度模型最优截短形式沿周期表的纵向作规律性变化,如孔洞型碳酸盐岩、火山岩储层饱和度计算模型等。

4 周期表应用实例

饱和度方程在矩阵中分布的周期变化规律:当储层导电呈并联模式时其饱和度模型最优截短形式沿周期表的横向作规律性变化;当储层导电呈串联模式时其饱和度模型最优截短形式沿周期表的纵向作规律性变化;当储层导电呈串并联混合模式时其饱和度模型最优截短形式沿周期表的对角线方向作规律性变化。下面以电性受多种因素影响的缝洞型碳酸盐岩和天然气水合物2类储层的饱和度模型确定为例展示周期表的实际应用。

4.1 缝洞型碳酸盐岩储层

碳酸盐岩储层除孔洞外,往往裂缝发育,缝洞储层即指储层中孔洞、裂缝均比较发育,且对岩石电性具有显著影响的储层。为便于分析,在电性规律研究时可将缝洞储层分解为孔洞储层加裂缝进行等价处理。对于孔洞型储层,其饱和度模型的形式如式(6)或式(7),上述2式中等号右边第2项体现了孤立孔洞对电性的“串联”影响。由于含裂缝岩心驱替困难,难以进行岩电测量,而数值模拟可以克服岩心试验的不足,通过对含裂缝岩心进行数值模拟可以研究裂缝对岩石电性的影响[22]。图2为裂缝对电阻增大率影响的数值模拟结果,其中基质代表不含裂缝的全直径岩电试验结果。

图2 缝洞型储层电性特征

岩电试验数据分析表明,不含裂缝基质电阻增大率与含水饱和度之间的关系式为

(12)

当存在裂缝时,岩心电阻增大率与含水饱和度之间的关系式为

(13)

对塔里木盆地某区块缝洞型碳酸盐岩储层全直径岩心电阻率试验数据分析表明,式(12)中参数h1=7.30,θ1=3.70,p1=0.98。当裂缝孔隙度为0.000 6时,式(13)中h2=0.27,其他参数与式(12)完全相同。试验、模拟结果及数据拟合分析如图2所示。

从饱和度模型周期表的结构看,式(13)在周期表的第2行第2列。对比式(13)与式(12)可以发现,式(13)中等式右端第一项中的分母中多了一项0.27Sw,该项正是裂缝对电性影响的反映。式(13)在周期表中的位置为第2行第2列,这与根据前述串并联模式下饱和度模型周期变化规律确定的位置完全一致。

4.2 天然气水合物储层

图3 不同饱和度情况下水合物在地层中的分布状态

通过对模拟低温高压环境下水合物电阻率试验结果[23](图4)分析表明,水合物饱和度方程为

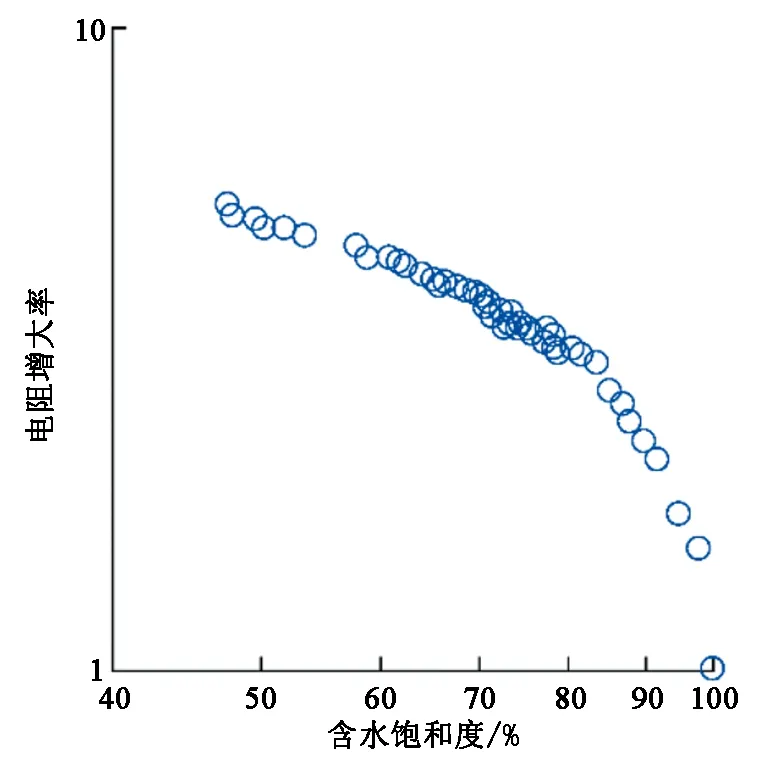
图4 水合物饱和度-电阻增大率试验关系

(14)

水合物饱和度计算方程(14)右端由3部分构成。研究表明,方程(14)中每一项都具有特定的物理意义,并与水合物的特定分布形式对应:①当水合物颗粒完全分布于地层岩石孔隙中时,类似于常规孔隙性砂岩储集层的油气饱和度计算,水合物饱和度计算方程(14)只有第1部分,即简化为Archie公式;②当水合物颗粒不仅分布于地层岩石孔隙中而且以颗粒方式支撑时,水合物饱和度计算方程具有2项,即式(14)中第1部分和第2部分;③当水合物颗粒不仅以颗粒方式支撑分布于地层岩石孔隙中,而且多到单独成层时,其饱和度计算方程同时具有式(14)中第3部分。图5给出了不同赋存状态水合物饱和度与式(14)中饱和度模型不同部分的对应关系。

图5 不同赋存状态水合物饱和度与电阻增大率关系

由于天然气水合物的电阻率很高,无论水合物是以分散颗粒、颗粒支撑还是成层状存在,水合物含量的增加都会使得储层电阻率增加,水合物本身对整体电性的影响呈现明显的“串联”特征,因此饱和度方程(14)中后2项均以直接相加的形式呈现。因此从形式上而言,饱和度方程(14)位于饱和度模型“周期表”中第4行第1列。对于饱和度模型的选择,不能仅仅停留在试验或模拟数据的拟合精度上,而是需要结合电性影响内在机制分析,选择既具有物理意义又具有理想精度的最优截短形式。饱和度模型周期表揭示了饱和度方程最优截短的一般规律,可以预测不同类型储层饱和度方程最优截短形式,对复杂储层饱和度模型的准确确定具有重要意义。