分数阶扩展卡尔曼滤波算法的锂电池SOC估算

安治国,周志鸿,伍柏霖

(重庆交通大学 机电与车辆工程学院, 重庆 400074)

0 引言

随着环境污染和石油资源的枯竭,新能源的开发引起了世界各国的重视,电动汽车发展迅速,动力电池储能技术成为研究热点[1-2]。锂离子电池由于其零排放、能量密度高、安全性能好且循环寿命长成为电动汽车的首选能源[3]。电池管理系统可以对电池能量进行有效管理并防止电池过充过放,同时可以防止电池温度异常产生安全性问题。电池电荷状态(SOC)是表征剩余电池容量的一个重要指标,是电池管理系统对电池进行有效监控和管理的重要参数之一,因此,对电池SOC的精确估算有着重要的意义[4-5]。

目前,许多学者对锂离子电池SOC估算做了大量的研究,提出了许多可行的方法。安时积分法计算简单,但对初值要求较高,容易产生误差累计[6-7]。开路电压法需要长时间的电池静置,不适用于实际中的电池SOC在线估计[8]。卡尔曼滤波算法是一种最小方差下对数据处理的算法,其基本思想是采用线性均方最小值准则,结合测量数据,通过递归方程更新各个参数,从而得到线性系统状态变量的最优估计值。扩展卡尔曼滤波算法在工程上应用较为广泛,但其线性化过程导致大量精度缺失,需要较高的模型精度,才能达到很好的滤波作用[9]。

卡尔曼滤波算法的准确性依赖于电池模型的精确性。常用的电池模型有电化学模型和经验模型[10],电化学模型精度高,但由于模型复杂,辨识参数多且难以得到,在汽车电池管理系统中应用较少;经验模型,用简单的电阻和电容元器件来描述电池内部特性,参数较少且容易获得,被广泛应用于车用锂电池SOC估算领域。Macdonald[11]、Westerlund[12]及Tian[13]等发现电容及电池均具有分数阶性质。传统的等效电路模型为整数阶模型,不能准确地反应电池内部复杂的非线性特性。Monje等[14]发现非线性系统具有分数特性,采用分数阶表达的系统更为精确。结合分数阶理论与扩展卡尔曼滤波在一定程度上弥补了系统的缺陷,可以有效提高电池SOC估计精度。

本文针对锂离子电池内部复杂的非线性情况,采用二阶分数阶电池等效电路模型,并应用遗传算法对模型参数进行辨识,基于分数阶微积分理论建立分数阶扩展卡尔曼滤波算法(FEKF)模型,并验证该SOC估算模型的有效性。

1 电池模型

1.1 电池等效电路模型

电池电化学阻抗谱(electrochemical impedance spectroscopy,EIS)测试通常是对电化学系统添加一个频率不同的小振幅交流正弦电势波,测量交流电势与电流信号的比值(系统的阻抗)随正弦波频率ω的变化,或者是阻抗的相位角f随ω的变化。采用EIS测试绘制出的Nyquist图描绘电池电化学阻抗谱,如图1所示。图1中阻抗的实部为横轴,虚部为纵轴。高频部分是由于尾部集流体引起的,阻抗谱曲线和轴线交点即表示为电池欧姆内阻;中频部分的弧线是由于电荷转移现象和双电层效应引起的,通常用RC并联电路来表示。但在传统的等效电路模型中,理想电容的阻抗特性只有虚部而没有实部,不能准确地描述电池内部固液交界处的双电层效应,因此,用恒相位元件(CPE)代替传统的理想电容可以提高模型的精度[15-16]。低频部分曲线表现了锂离子在固相中的扩散现象,也可以用CPE元件表示。二阶RC电路精度更优,适用于电池单体的估算[17-18]。

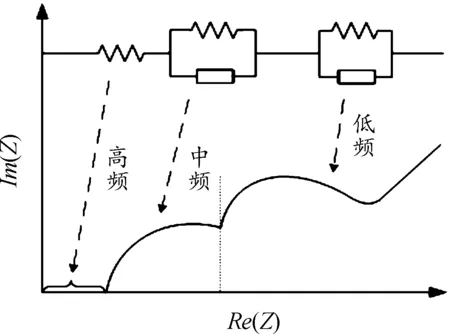
图1 电池电化学阻抗谱Nyquist

图2为电池分数阶等效电路模型,R1代表电荷转移电阻,R2代表电化学极化电阻,CPE1与R1并联代表电池双电层效应,CPE2与R2并联代表电池的扩散效应,R0代表欧姆内阻,UOCV代表开路电压,Ut代表端电压。

图2 电池分数阶等效电路模型

恒相位元件(CPE)是一种常见的电路元件,它在频域内的传递函数式定义如下：

(1)

式中：S=jω=j(2πf),f为工作频率;α为弥散系数(0<α<1),它反映了电极双电层偏离理想电容的性质;Y为导纳常数。当α=1时,CPE元件表示一个理想电容;当α=0时,CPE元件表示一个电阻。

1.2 分数阶电池SOC估计模型

电池SOC计算公式为剩余电荷量与实际电荷量百分比[19-20],其定义式如下：

(2)

式中：ηc为电池充放电库伦效率;CN为电池实际满电时的容量;i(t)为电流时间函数。

分数阶微积分定义有多种形式,其中3种重要的定义形式分别为Grünwald-Letnikov(G-L)定义、Riemann-Liouville(R-L)定义和Caputo定义。此处选取(G-L)定义式[21-22]：

(3)

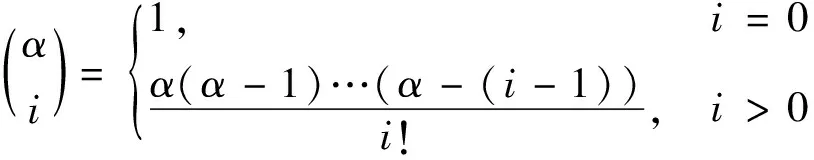
(4)

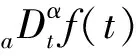
根据分数阶电池模型和基尔霍夫电流电压定律可以列出式(5)及式(6)：

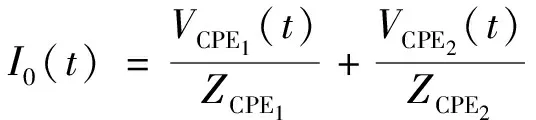
(5)

VOCV(t)=VT(t)+IT(t)R0+

VCPE1(t)+VCPE2(t)

(6)

并联RC电路的微分表达式为

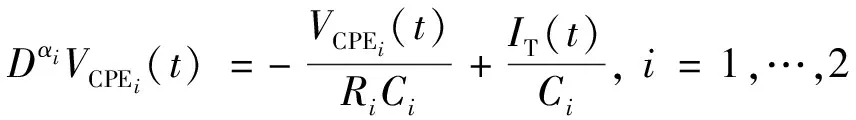
(7)

SOC的微分表达式为：

(8)

由式(5)到式(8)可得电池模型的数学表达式

(9)

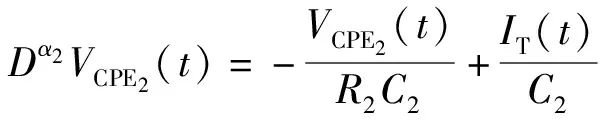
(10)

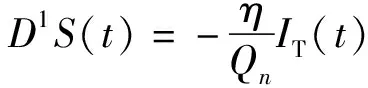
(11)

VT(t)=VOCV(S(t))-IT(t)R0-

VCPE1(t)-VCPE2(t)

(12)

根据式(9)到式(12)写出分数阶等效电路模型的矩阵形式。

状态方程为

(13)

输出方程为

VT=VOCV(S)-ITR0-VCPE1-VCPE2

(14)

令τ1=R1C1,τ2=R2C2,根据式(3)及式(13),k+1时刻状态方程可写成式(15)。

(15)

式(15)进一步简化,η取1[23],可得式(16)：

(16)

状态方程最终写为

(17)

yk+1=Cxk+1-R0uk+1+VOCV

(18)

1.3 FEKF估算流程

根据式(17)和式(18)可得：

(19)

式中：wk和vk+1分别表示k时刻和k+1时刻的过程噪声和测量噪声,两者均为不相关的零均值高斯白噪声。

对g(·)进行线性化：

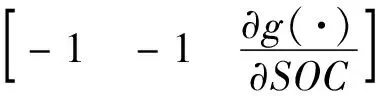
(20)

式(20)可以简写为

(21)

分数阶扩展卡尔曼滤波算法步骤如表1所示。

表1 分数阶扩展卡尔曼滤波算法步骤

式中：Qk、Rk分别是系统的过程噪声协方差和测量噪声协方差,I是单位矩阵。

2 电池模型参数辨识

2.1 R0识别

准确识别对于模型的估算精度至关重要,采用锂电池内阻测试仪对电池内阻进行测量。内阻试验所用仪器为安柏AT521电池内阻测试仪,如图3所示,其电阻测试范围为10～32 Ω,精确度为0.5%。分别测试了3种SOC(100%、50%和0%)状态下的R0值,分别为1.94、2.02、2.05 mΩ,并求得其平均值,为2.00 mΩ。

图3 试验设备

2.2 [R1、R2、CCPE1、CCPE2、m、n]参数辨识

遗传算法(Genetic Algorithm)鲁棒性和全局寻优能力强,适合多参数识别,流程如图4所示。采用遗传算法对电池的R1、R2、CCPE1、CCPE2、m和n进行识别。

图4 遗传算法流程

优化目标函数定义如式(22),使端电压估计值和测量端电压的残差平方和最小[24]。

(22)

适应度函数定义如下：

(23)

当目标函数越小时,估计值和测量值越接近,则寻优结果越好,适应度函数值越大。设置适应度函数达到0.95时,参数识别结束,输出识别参数结果。

遗传算法中所需的电压数据可以根据混合脉冲功率性能测试(HPPC)试验进行采集,具体过程为：以1C倍率对锂电池进行放电34 s,并静置电池3 min;随后,以0.75C倍率放电34 s,并静置电池3 min;最后,再以1C倍率放电5 min,并静置 3 min,重复执行上述步骤9次,每个循环周期内使电池放电10%SOC获得其电压及电流数据。对试验获得数据进行参数辨识,结果如表2。

表2 各参数辨识结果

3 电池充放电试验与仿真分析

3.1 电池恒流放电试验

选用的电池为山东威能方形磷酸铁锂电池,电压范围2.5～3.65 V,容量40 Ah,截止电流2.6 A。电池充放电试验的环境温度为25 ℃,充电设备为贝奇CH9800可编程智能充电器,负载精度为±(0.05%+0.03%FS),电压分辨率为0.1 mV,电流的分辨率为0.1 mA。

电池放电试验步骤为：先将该电池充电至100%SOC后,静置1 h;随后,以1C电流放电至95%SOC,再将电池静置1 h,记录此时电池端电压。重复上述过程20次,每个周期放电5%SOC,直至电池放电至截止放电电压2.5 V。

通过以上实验所得数据可以拟合出SOC-OCV关系图,再由估算电压插值得出电池SOC值,公式拟合的阶数和精度会直接影响电池SOC估算结果的准确性。再次将试验所得数据,采用9阶多项式拟合,得式(24)。多项式系数如表3所示,曲线如图5所示。

表3 多项式系数

图5 电池SOC和OCV的关系

Uoc(SOC)=P1SOC9+P2SOC8+P3SOC7+

P4SOC6+P5SOC5+P6SOC4+

P7SOC3+P8SOC2+P9SOC1+P10

(24)

3.2 DST试验

对选取的电池进行充放电测试,基于恒惠HSP-6015型直流充电设备、贝奇CH9812型放电设备在恒温箱进行试验,如图3所示。

参照手册[25]设计DST试验,具体试验步骤如表4所示。

表4 DST试验步骤

重复DST试验步骤6次,当电压放至截止电压,试验结束。在试验设备输入以上的试验步骤,并对其电流电压数据进行采集。所得的电压及电流随时间变化的曲线如图6。

图6 DST试验电流、电压与时间的关系

3.3 结果及讨论

从图7、图8及表5中可以看出,与整数阶等效电路模型相比,分数阶电池模型估算的电压对真值具有更好的跟随性。从图8可以看出,其稳定性更优,且误差均值、最大值和均方根值都小于传统模型误差,证明分数阶模型较整数阶等效电路模型能更好地表达电池内部非线性特性。

表5 电压误差均值和最大值

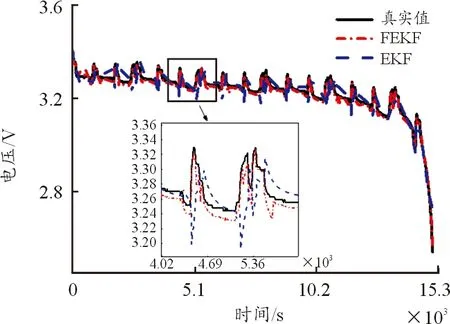
图7 端电压与电压估计值对比

图8 端电压估计值误差对比

从图9、图10及表6中可以看出,分数阶扩展卡尔曼滤波和扩展卡尔曼滤波在DST工况下,分数阶扩展卡尔曼滤波对SOC的估计更为精确。从图10中可以看出,分数阶扩展卡尔曼滤波的波动更小,误差均值、最大值和均方根值都小于扩展卡尔曼滤波。证明,将分数阶理论结合到扩展卡尔曼滤波算法中,能有效地提升算法对SOC的估算精度。

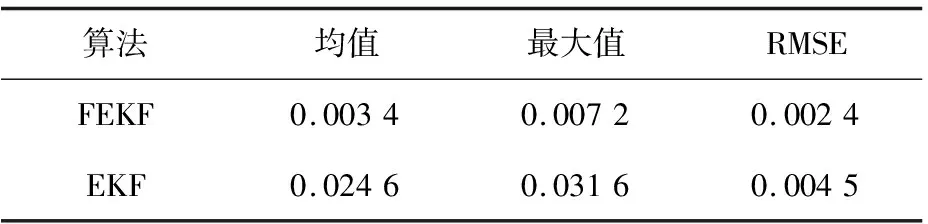
表6 SOC值误差均值和最大值

图9 SOC真实值与估计值对比

图10中,在仿真开始,2种算法都出现尖峰,这是由电池放电时产生的极化现象导致,分数阶算法误差峰值更低,且在零值附近小幅波动。整数阶算法的误差在放电的周期明显高于分数阶误差,仅在临近放电结束时,误差接近于零。在电池放电临近结束时,由于内阻发生明显变化,分数阶算法产生较大的误差,这就表明分数阶算法对参数准确度的依赖性高于整数阶算法。

4 结论

通过对汽车动力电池的非线性特性进行研究,从电池电化学阻抗谱图中表现的性质对电池等效电路模型进行改进,提出了二阶分数阶等效电路模型。采用遗传算法对电池的参数进行识别,并将试验与仿真相结合,对提出的分数阶电池模型和分数阶扩展卡尔曼滤波算法进行验证对比,得到以下结论：

1) 用恒相位代替传统理想电容建立的二阶分数阶等效电路模型能有效提高模型精确度,从而明显提高SOC估算精度。

2) 与EKF相比,FEKF算法的SOC估算结果更接近真实值,波动性更小、更稳定,均方根误差(RMSE)仅为0.24%。

3) 相对于整数阶算法,分数阶算法误差峰值更低,波动幅度更小,在放电临近结束时,由于电池内阻的变化,分数阶算法误差增大。