基于多源数据和广义回归神经网络的ZWD预报模型

黎峻宇,姚宜斌,刘立龙,张 豹,黄良珂,曹利颖

1. 桂林理工大学测绘地理信息学院,广西 桂林 541006; 2. 广西空间信息与测绘重点实验室,广西 桂林 541006; 3. 武汉大学测绘学院,湖北 武汉 430079

GNSS信号穿过对流层时,产生的延迟(对流层延迟)是GNSS导航定位的主要误差源之一。由于难以准确测量信号传播路径上的对流层延迟,因此需要对其进行模型化。常用的方式是确定天顶方向的对流层延迟(ZTD),然后将其乘以投影函数,以获得斜路径的对流层延迟。可见,准确模型化ZTD是削弱对流层延迟影响的重要工作。根据影响因素的不同,ZTD可分为天顶对流层静力学延迟(ZHD)和天顶对流层湿延迟(ZWD)。其中ZHD占到ZTD的90%左右,可通过实测气象数据和经验模型精确计算,精度达毫米级[1]。因水汽等因素引起的ZWD由于水汽剧烈的时空变化,其变化率最高可达ZHD的4倍[2-3],难以准确计算,是制约GNSS对流层改正的主要因素。此外高精度的ZWD先验值可提高GNSS精密单点定位的收敛速度、优化坐标高程分量的精度[4-5]。因此,建立高精度的ZWD预报模型具有重要的现实意义。学者们在模型化ZWD方面做了很多努力,构建的模型主要分为:基于实测气象参数的模型和经验模型。前者如Hopfield模型[6]和Saastamoinen模型[1]依赖实测温度、相对湿度和压强等气象数据,改正精度可达厘米级。后者只需要测站坐标和时间作为基本输入信息,在实际工作中应用更广,尤其对于GNSS实时应用。文献[7—8]基于美国标准大气数据提取的气象参数年平均值和年周期振幅网格表,构建了UNB系列模型。该系列模型基于15°为一个纬度带的网格表和顾及气象参数年周期变化的三角函数计算ZWD,其中UNB3m模型的平均精度为5.5 cm[9]。文献[10—12]利用美国国家环境预报中心气象再分析资料,基于考虑气象参数或ZWD年周期变化、日周期变化的三角函数,构建了1°×1°的TropGrid系列模型。文献[13]利用欧洲中尺度天气预报中心的ERA-interim气象再分析资料,基于顾及年周期和半年周期变化的函数对5°×5°和1°×1°气象参数进行周期性拟合,建立了全球格网模型GPT2w。GPT2w是当前国际公认计算ZWD精度最高的模型[14-16]。此外,学者们基于类似的方式建立了一些相近的模型[17-19]。

由前人研究可知,当前主流的经验模型大多基于再分析资料等单源数据,且通过模型函数表征ZWD在不同尺度上的变化方式,难以反映ZWD在不同尺度的非线性复杂变化。机器学习算法是通过对数据进行自动分析并获取规律,进而利用发现的规律对未知数据进行预测的算法,其在处理当前规律尚未明确的复杂非线性问题方面优势突出[20-21]。文献[22]通过反向传播神经网络(BPNN)建立了Hopfield估算ZTD误差的抵偿模型,抵偿模型的均方根误差优化了超过90%。文献[21]基于BPNN构建了对流层参量加权平均温度模型,该模型相对两种精度较高的经验模型性能明显提升,再次证明了机器学习算法在对流层参量建模方面的优越性。广义回归神经网络(generalized regression neural network,GRNN)基于非线性回归理论进行函数估计,并根据最大概率原则计算网络输出向量。与传统神经网络相比,GRNN的训练过程更加方便,特别适合解决曲线拟合问题,已在各学科和工程领域得到广泛应用。鉴于ZWD时空变化剧烈的特点,本文基于多源数据和GRNN构建一个高精度的ZWD预报模型,并对模型精度进行检验。

1 研究区域与数据源

1.1 研究区域

本文选择了纬度15°N—55°N和经度70°E—135°E的区域开展研究。该地区覆盖中国大陆和部分周边国家与地区,地形复杂,气候模式多样,陆-海作用强烈,导致ZWD时空变化剧烈[23]。得益于此,本区域或为研究高精度ZWD预报模型的理想试验场,然而,复杂的自然条件也为高精度模型的建立带来诸多挑战。此外,该区域有庞大的北斗/GNSS实时用户,如果能为其提供高精度的ZWD预测值,对于提高中国及周边地区北斗/GNSS实时应用的精度具有积极推动作用。

1.2 数据源

本文所用数据包括中国气象局新一代中尺度版本全球/区域同化和预报系统(GRAPES_MESO)数据、ECMWF第五代再分析资料(ERA5)和全球无线电探空综合档案(IGRA)。GRAPES_MESO的水平分辨率为0.1°×0.1°,垂直分辨率为1000 hPa到100 hPa,共8层,时间分辨率为3 h。使用了研究区域内GRAPES_MESO所有格网点2016、2017年温度、水汽压和位势高垂直廓线预报数据的存档资料来计算ZWD(记为GRAPES ZWD),具体公式如下

(1)

Nw=k2×e/T+k3×e/T2

(2)

式中,Nw表示湿折射率;k2=64.79 K/hPa,k3=377 600 K2/hPa;e为水汽压,单位为hPa;T为温度,单位为K[24]。

ERA5数据的时间分辨率为1 h,空间分辨率为0.25°×0.25°。使用了从1000 hPa至1 hPa 37个气压层的数据来计算ZWD(记为ERA5 ZWD),计算方法与GRAPES ZWD相同。ERA5气压分层数据不直接提供水汽压,因此采用了文献[25]的方法基于温度、相对湿度计算水汽压。

无线电探空仪可以测量多种大气参数,是大气研究的重要手段。探空相对湿度和温度的精度分别可达3%和0.2 K[26]。由于其高精度、高可靠性,探空数据常被用于评估模型的精度[14,19]。因此,使用了IGRA提供的2016、2017年146个探空站数据计算ZWD,记为RS ZWD,并将其用于建模和检核,时间分辨率为12 h,方法同前。需要说明的是,利用RS ZWD进行检核前,需要把GRAPES/ERA5 ZWD插值到探空站的位置。首先利用当前已知ZWD高程改正精度最高的方法[14],将探空站附近4个格网点的ZWD改正到探空站高度,然后通过双线性水平插值到探空站位置。格网GRAPES/ERA5 ZWD覆盖范围和探空站点位分布见图1,其中三角形表示参与建模的探空站,圆点表示检核探空站。

图1 格网GRAPES/ERA5 ZWD覆盖范围及探空站点位分布Fig.1 The coverage area of the grided GRAPES/ERA5 ZWD and distribution of radiosonde stations

2 基于多源数据和GRNN的ZWD预报模型

已有的ZWD模型大多基于单一数据源,如再分析资料、数值天气预报数据或探空数据的一种。基于前两种数据的模型时空分辨率较高(最高可达0.1°×0.1°和1 h),然而在局部地区精度损失较大,尤其在用于同化的气象站稀疏、高程起伏大和天气变化较为剧烈的地区[27],如中国的青藏高原。基于后者的单站模型精度较高,但由于探空站的水平分辨率约为250 km,模型应用范围较小,且时间分辨率一般只有12 h。本文利用两种数据源的优点,提出基于多源数据构建ZWD预报模型的方法。GRNN属于前向传播的神经网络,不需要反向传播求模型参数,学习速度快,不需要迭代过程[28]。这些优点使得GRNN成为了处理回归、近似、拟合和预测问题的强大工具。本文正是利用GRNN的这些优点,构建了基于GRNN的ZWD预报模型。

2.1 GRNN模型

GRNN的理论基础是非线性回归分析。在GRNN中,假设有随机变量x和因变量y,其概率密度函数为f(x,y),且x的观测样本为X,则y的条件期望为

(3)

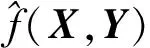
(4)

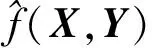
(5)

则高斯核可表示为

(6)

对式(3)进行积分可得

(7)

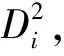
2.2 基于GRNN的ZWD预报模型

ZWD受时空影响较大[13,30],且经验值的输入可改善机器学习模型的性能[21,28]。基于此,构建了基于GRNN的ZWD预测模型(GRNN-F)训练框架,如图2所示。与预设函数的模型固定ZWD的时变特征不同,GRNN网络是数据自适应的。

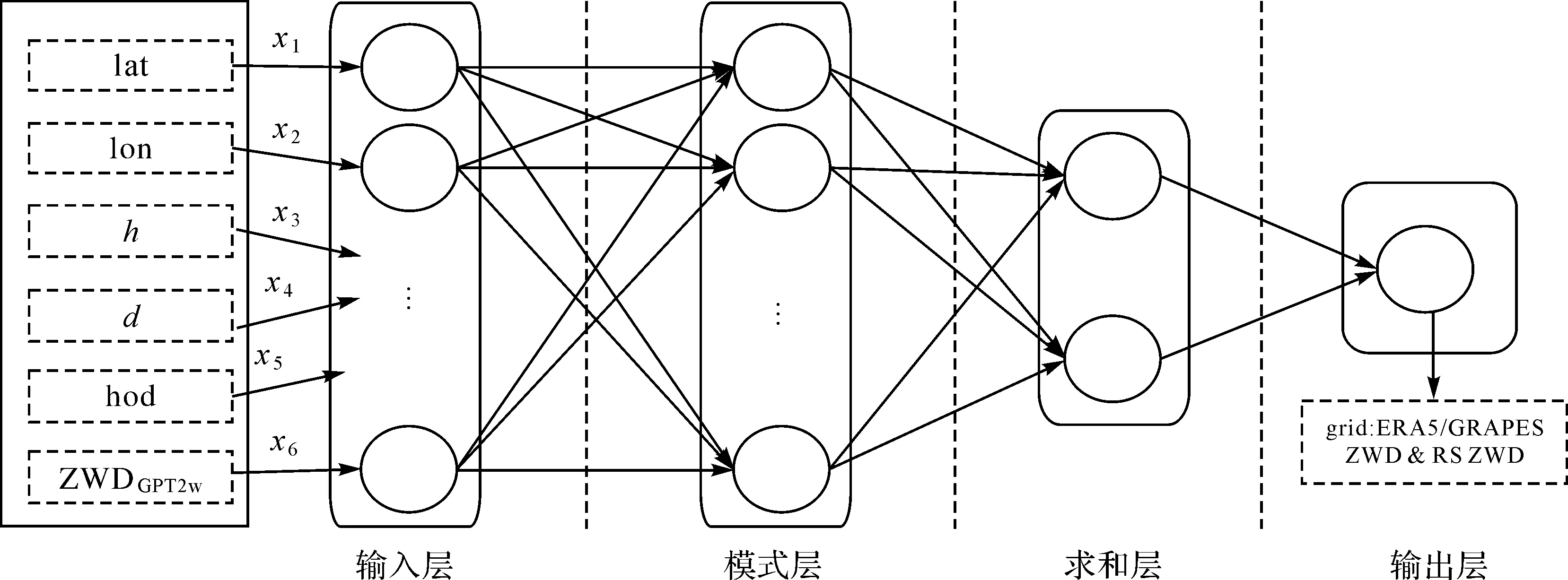
图2 GRNN-F的训练框架Fig.2 The training framework of GRNN-F

图2输入层中lat、lon和h分别为测站纬度、经度和高程;d和hod为年积日和UTC时;ZWDGPT2w为GPT2w估算的经验ZWD(GPT2w-ZWD)。输出层为优化、降采样后的格网ERA5/GRAPES ZWD(见2.2.1节)与RS ZWD的合并数据集。基于图2框架训练好的模型,输入三维坐标、时间和GPT2w-ZWD即可得到ZWD的预测值,记为GRNN-F-ZWD,则有

GRNN-F-ZWD=g(lat,lon,h,d,hod,ZWDGPT2w)

(8)

式中,g表示GRNN-F模型。此外,为突出基于多源数据建模的优越性,仅利用参与了GRNN-F建模的RS ZWD作为训练时的输出,基于与GRNN-F相同的训练框架和输入变量建立了一个基于单源数据(RS ZWD)的ZWD预报模型,简称GRNN-R。将三维坐标、时间和GPT2w-ZWD输入GRNN-R即可得到ZWD预测值(记为GRNN-R-ZWD),输入和输出的关系可表示为

GRNN-R-ZWD=g(lat,lon,h,d,hod,ZWDGPT2w)

(9)

需要说明的是,GPT2w并不直接输出ZWD,用户基于GPT2w输出的气象参数计算ZWD,具体公式如下[31]

(10)

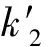
2.2.1 数据预处理

高质量的训练样本有利于构建高精度的GRNN模型,因此在建模前对格网ERA5/GRAPES ZWD进行了优化。优化的基本思路是:利用GRNN以146个探空站处高质量的RS ZWD为输出,插值到探空站处的ERA5/GRPES ZWD、测站三维坐标、时间为输入的网络结构来拟合它们之间的关系,进而建立以测站三维坐标、时间和ERA5/GRAPES ZWD为输入,优化后的ERA5/GRAPES ZWD为输出的优化模型,具体的方法和步骤见文献[29]。将格网ERA5/GRAPES ZWD及对应三维坐标和时间输入优化模型,即可获得优化后的格网ERA5/GRAPES ZWD。以RSZWD为参考值,插值到探空站处的ERA5/GRAPES ZWD优化前后的精度见表1。

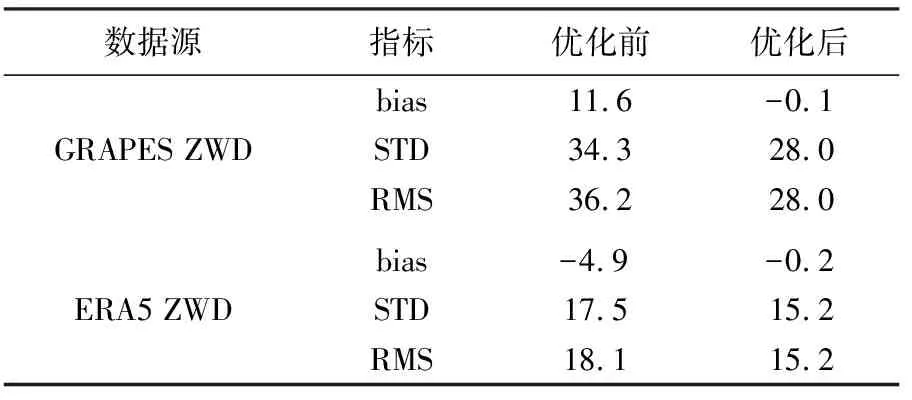
表1 优化前后插值到探空站处GRAPES/ERA5 ZWD的精度

显然,优化后GRAPES/ERA5ZWD的bias都减小到接近0 mm,RMS均小于3 cm。这对于基于实测气象数据估算也仅能达到厘米级精度的ZWD而言,优化效果是非常显著的,可认为优化后的GRAPES/ERA5 ZWD与RS ZWD是无偏的。

此外,多源数据的引入,相对单源数据建模,数据量剧增。假如仅以146个探空站数据建模,不计数据缺失两年仅有213 452个时刻文件。引入GRAPES数据(1 526 626 248个时刻的文件)和ERA5数据(737 216 424个时刻文件)后,数据量增加了约1.1万倍。如果将所有的数据均用于训练模型,会带来训练时间过长的问题。为合理选择建模数据的分辨率,分析了平均海平面处ERA5 ZWD在经纬度方向变化特征(图3)的基础上,对优化后的格网GRAPES/ERA5 ZWD进行了降采样。

图3 2016年平均海平面年均ERA5 ZWD随经纬度的变化Fig.3 The variations of the annual mean sea level ERA5 ZWD with latitude and longitude in 2016

由图3可知,ZWD整体随着纬度增加而降低,下降率为-6.36 mm/(°);ZWD随经度增大而增大的趋势明显,上升率为0.55 mm/(°),其原因可能是由于研究区域内,经度越大越靠近海洋,同时西高东低加之山脉的阻隔导致来自海洋的水汽难以进入西部地区,主要由水汽引起的ZWD整体西小东大。说明在研究区域内,ZWD在纬向和经向上分别跨越0.5°和5°产生的变化约为3 mm,与RS ZWD的平均精度[32]相当。因此,在同时顾及模型精度和训练时长的基础上,将优化后的格网GRAPES/ERA5 ZWD降采样至0.5°×5°(纬度×经度),联合120个站的RS ZWD用作建模,此外选择了26个分布相对均匀站的RS ZWD用作检核。建模站和检验站见图1的三角形和圆点。

2.2.2 模型训练

由2.1节可知,GRNN模型训练主要以σ为研究对象。选用了后验寻优的方法确定σ,即用不同的σ去训练GRNN模型,每次训练都采用十倍交叉验证[33]的精度去检验训练效果。基本思路是:对于每个σ,用90%的数据(包括输入变量和输出参考值)训练GRNN模型,10%的数据(参考值)用于检验,既可以保证验证结果具有更好的可靠性[33],还可以使更多的样本参与建模,这样交叉验证的结果更接近最终的模型;这个过程进行10次,确保所有数据都参与了训练和检验,统计检验值与模型预测值差值的RMS,并以RMS最小为准则来确定最佳σ。基于参考文献[28—29]取得良好效果的σ寻优方式,本文采用范围为0.01～1(间隔为0.01)的σ值来重复训练过程。需要说明的是,本文为了加快模型训练速度,每月建立一个模型,然后将12个月的模型代码存放到一起以供不同时刻调用,组成最终的模型。图4给出了用不同的σ训练8月GRNN模型对应的RMS。

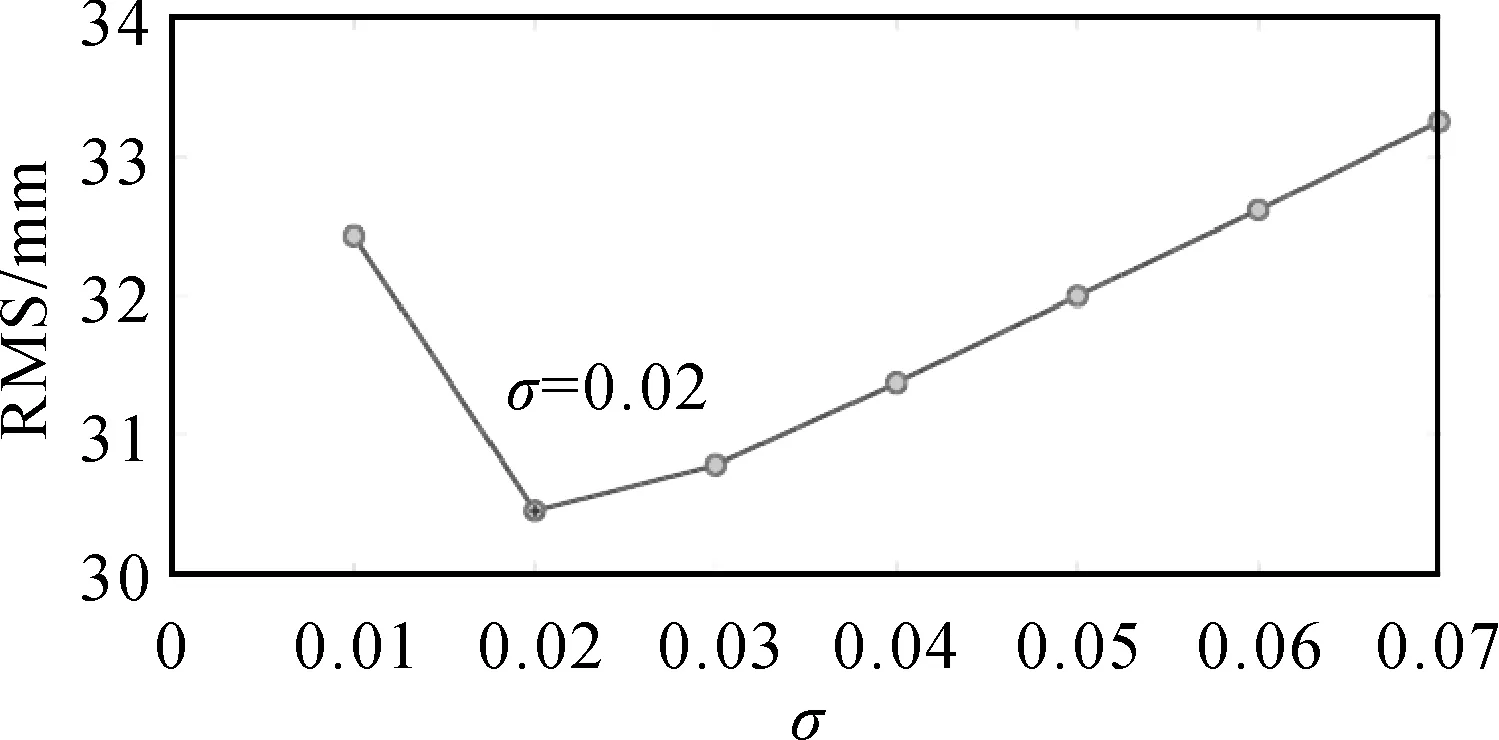
图4 不同σ训练8月GRNN模型的RMSFig.4 RMS from GRNN based on different σ in August

由图4可以看出,σ先急剧下降,然后逐渐增大,等于0.02时RMS最小。因此,选用σ=0.02来训练8月的GRNN-F模型,其他月份的σ确定方式相同。1—12月的σ分别为:0.02、0.03、0.03、0.02、0.02、0.02、0.02、0.02、0.02、0.02、0.03和0.02。

3 模型精度检验

3.1 内符合精度和优越性分析

3.1.1 内符合精度

为检验建模方法的合理性,利用参与建模的数据检验GRNN-F的内符合精度,统计了其估算ZWD的平均bias、STD和RMS。结果表明,GRNN-F-ZWD的bias为0,且STD、RMS均等于24.1 mm,内符合精度达到厘米级。这样的内符合精度与依赖实测气象数据模型估算ZWD的精度[3]相当,说明GRNN-F具有良好的拟合效果。

ZWD受纬度和高程影响较大,为反映GRNN-F内符合精度在纬度和高程上的变化,统计了GRNN-F在各纬度和高程段的内符合精度(图5)。显然,GRNN-F-ZWD的bias绝对值先随纬度增加有所增大,纬度大于35°N之后整体呈减小趋势,但最大值小于0.2 mm;在15°N～35°N之间,STD/RMS基本相等且相对较大,但最大值小于30 mm,纬度大于35°后逐渐减小。bias绝对值在约500 m以下的高程处相对较大,在其他高程段较小,且最大值小于0.5 mm;随着高程上升STD/RMS整体呈降低趋势,STD/RMS均小于30 mm。因此,在整个研究区域GRNN-F的内符合精度指标和变化幅度均在厘米级范围内,具有较高且稳定的内符合精度。

图5 GRNN-F内符合精度随纬度和高程的变化Fig.5 The variation with latitude and height of internal accuracy from the GRNN-F

由于ZWD有明显季节特性,统计了GRNN-F-ZWD 2016—2017每日的空间平均bias、STD和RMS,以检验GRNN-F内符合精度的季节变化(见图6)。显然,GRNN-F-ZWD的bias在0左右均匀分布,平均值为0(见图6(a)红色线),且无超过1倍STD(24.1 mm)的跳变;STD/RMS夏秋两季总体较大,冬季较小,但最大值仍小于48 mm。可见,GRNN-F的高内符合精度有良好的时间稳定性。

图6 GRNN-F内符合精度的时间序列Fig.6 The time series of internal accuracy from the GRNN-F

3.1.2 优越性分析

为展示本文所提建模方法的优越性和厘清基于多源数据或GRNN建模的优势,仅利用同时参与了GRNN-F和GRNN-R建模的120个站RS ZWD检验了GRNN-R和GRNN-F的精度,并与国际典范经验模型GPT2w(通过预设模型函数表征ZWD在不同尺度上的变化)直接估算ZWD的精度进行比较,结果见表2。

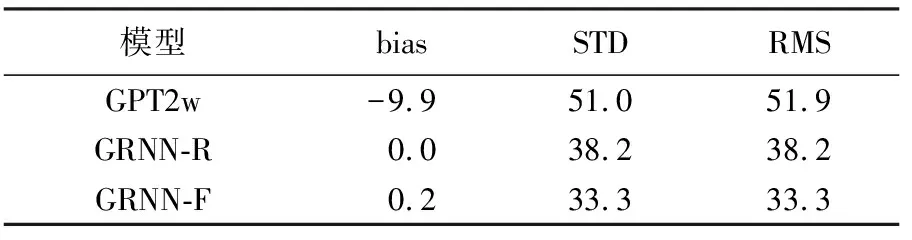
表2 不同模型估算120个参与建模站ZWD的精度

由表2可见,GRNN-R/GRNN-F-ZWD的bias绝对值、STD和RMS均明显小于GPT2w-ZWD,bias绝对值减少了近10 mm,以GPT2w-ZWD作为部分输入信息的GRNN-R和GRNN-F精度相对GPT2w有精度有明显提升。这意味着基于GRNN建模对GPT2w的经验值有精化作用,能有效提高拟合ZWD的精度。GRNN-F-ZWD的bias绝对值与GRNN-R-ZWD相当,其他各项指标均明显优于GRNN-R-ZWD,STD和RMS均减少了12.8%,可见引入更多高质量的数据(多源数据)建模同样有助于提高ZWD拟合的效果,同时再次证明2.2.1节中优化后的格网GRAPES/ERA5 ZWD与RS ZWD之间是无偏的。这些结果表明,基于多源数据和GRNN建模对于提升ZWD的拟合精度均有贡献,相对主流建模方式有一定的优势。

为了更清晰地展示本文所提建模方法的优越性,统计了3个模型在各建模站处的bias、STD和RMS(见图7)以及对应的每日空间平均值(见图8)。由图7可知,GRNN-F-ZWD和GRNN-R-ZWD在大部分地区的bias绝对值接近,约等于零,且几乎没有空间差异,相对GPT2w-ZWD有明显减少,在水汽含量大且变化较为剧烈的低纬度地区更明显,可能是由于GRNN-F/GRNN-R更好地拟合到了ZWD除GPT2w顾及的季节性变化之外的复杂变化;海陆交界处由于受海洋和陆地气候的综合影响,水汽变化频繁导致ZWD变化更为剧烈,给模型化带来了更大的难度,而GRNN-F-ZWD的bias在几个海陆交界处相对GRNN-R-ZWD仍有所减小,可见更高时空分辨率的多源数据有利于揭示ZWD更精细的变化。GRNN-F-ZWD和GRNN-R-ZWD的STD/RMS相对GPT2w-ZWD在各地区有不同程度的降低,在毗邻印度洋和太平洋的区域降低尤为明显,GRNN-F-ZWD在这些地区的STD/RMS相对GRNN-R-ZWD也有所减小,这些地区分别受东亚季风和南亚季风的影响,水汽含量高,ZWD变化剧烈,导致通过预设模型函数表征ZWD在不同尺度上变化的GPT2w精度在这些地区受到严重削弱,而基于GRNN的两个模型相对GPT2w在这些地区有更明显的精度改善,尤其是基于多源数据的GRNN-F。可见,本文的建模方式在研究区域的ZWD拟合方面具有明显优势,且在ZWD变化较极端的地区仍具有突出优势。图8表明,相对其他两个模型,GPT2w-ZWD的bias分布更加离散且波动较大;GRNN-F-ZWD和GRNN-R-ZWD的bias均匀分布在0左右,无过大跳变;两年间,GPT2w-ZWD的STD/RMS起伏最大、值也最大,GRNN-R-ZWD的值居中,GRNN-F-ZWD的值最小、离散性也最小,且出现了很多STD/RMS接近于0的时刻。总之,本文的建模方式在不同季节的ZWD拟合方面具有很好的优势。

图7 不同模型估算各建模站ZWD的bias、STD和RMSFig.7 The bias, STD and RMS of the ZWD from different models at each modeling station

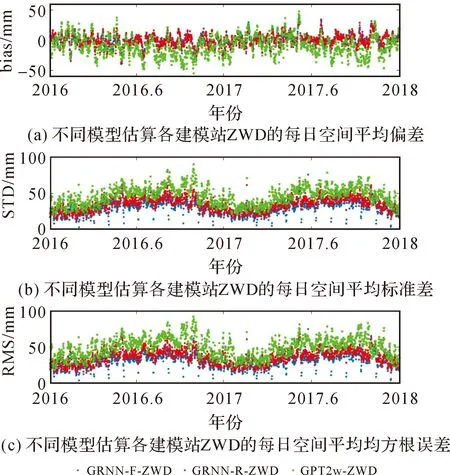
图8 不同模型估算各建模站ZWD的每日空间平均bias、STD和RMSFig.8 The spatially averaged daily bias, STD and RMS from different models' ZWD from each modeling station

3.2 外符合精度

为检验模型的适应性,使用了26个未参与建模站的RS ZWD来检验GRNN-F的外符合精度。表3为3个模型预报ZWD的总体精度。

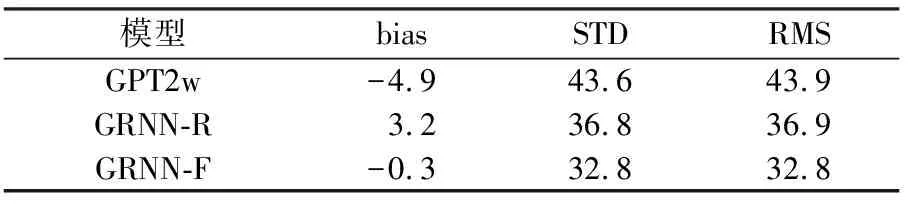
表3 不同模型预报未参与建模站ZWD的精度

显然,GRNN-F-ZWD的bias绝对值、STD和RMS均小于GPT2w-ZWD和GRNN-R-ZWD,精度有全面的提升。相对GPT2w-ZWD,GRNN-F-ZWD的bias绝对值减少近5 mm,STD和RMS分别降低了10.8 mm (24.8%)和11.1 mm(25.3%)。可见,GRNN-F不是一个简单的GPT2w精化模型,而是一个高精度的区域模型。相比GRNN-R-ZWD,GRNN-F-ZWD的bias绝对值减少了近3 mm,STD和RMS分别减少了4.0 mm (10.9%)和4.1 mm (11.1%)。说明基于多源数据的建模可以全面提升模型在整个区域预报ZWD的精度,再次证明了本文所提建模方法的优越性。此外,对比3.1.1节的结果和表3可发现,GRNN-F的内外符合精度很接近,模型并没有出现在非建模站点精度损失严重的情况,具有较强的适应能力。

为分析GRNN-F预报精度的空间稳定性,统计了3个模型预报未参与建模站ZWD的bias、STD和RMS随纬度(图9)和高程(图10)的变化。如图9,随纬度增加,3种模型的bias并无明显变化规律;GRNN-F-ZWD的bias绝对值最小,且最稳定,在0附近徘徊;3种模型的STD/RMS随着纬度的增大呈现整体减小的趋势,这是由于水汽含量更少的中高纬度地区ZWD小于低纬度地区,ZWD变化也更加稳定;GRNN-F-ZWD的STD/RMS在所有纬度节点相对其他2种模型均有所减少,在ZWD变化较剧烈的低纬度地区减少量更大,离散性最小,最大值仍小于50 mm。可见,GRNN-F-ZWD在各纬度段均具有较高的精度,且有很好的稳定性。如图10所示,3种模型的bias与高程关系并不明显;GRNN-F-ZWD的bias明显优于其他2种模型,尤其在稳定性方面,在0附近波动,最大绝对值小于20 mm;3种模型的STD/RMS整体与高程呈负相关关系,这是由于随着高程的增加水汽含量越来越低,ZWD变化更加稳定导致的;所有站点处GRNN-F-ZWD的STD/RMS均最小,振幅也最小,在ZWD变化更剧烈的低海拔地区优势更突出,峰值均小于50 mm。总体来说,GRNN-F的高预报精度在高程上有很好的稳定性。

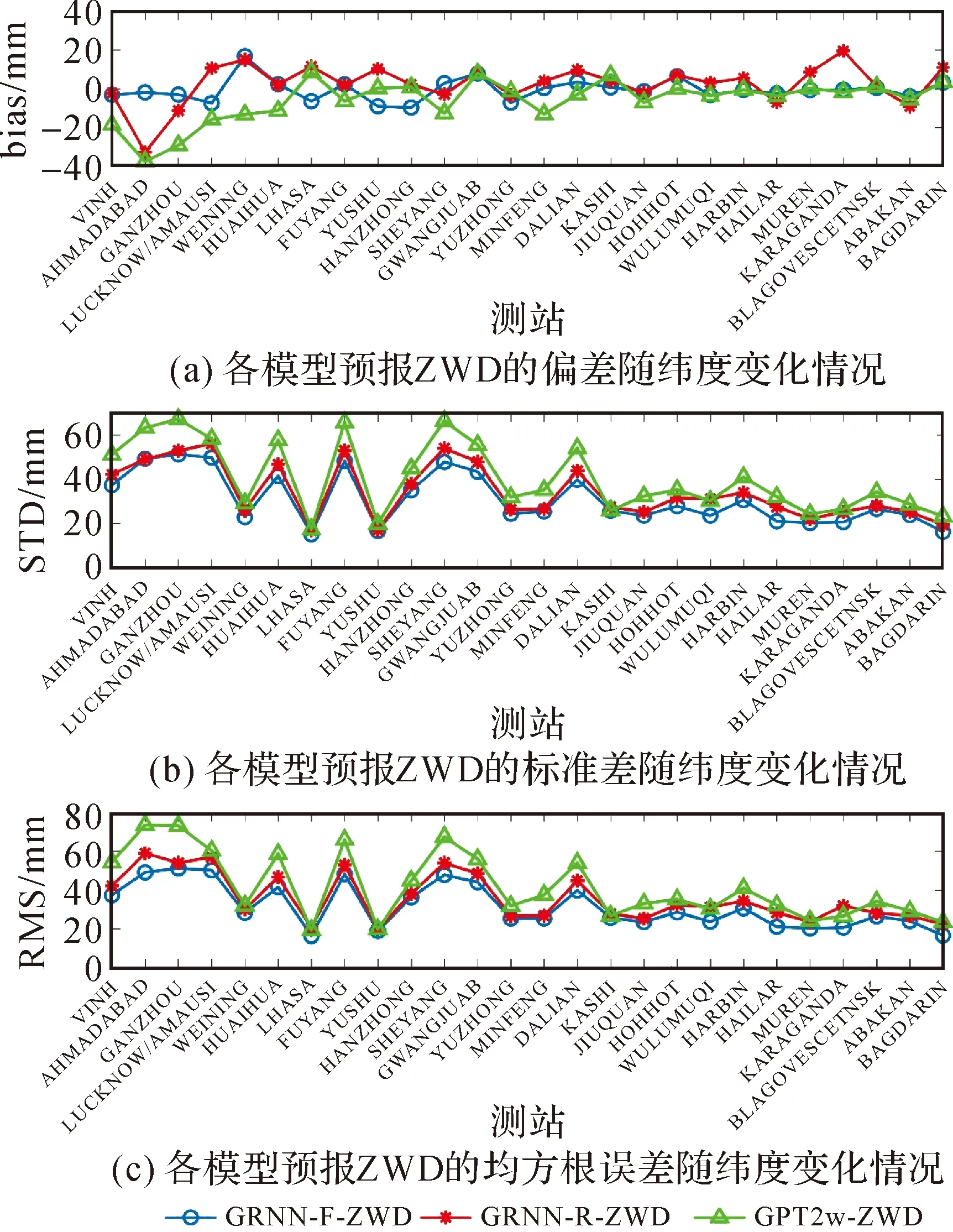
图9 各模型预报ZWD的bias、STD和RMS随纬度变化情况(站点随纬度升序排列)Fig.9 The bias, STD, and RMS of the forecasted ZWD from each model at RS stations sorted in ascending latitude

图10 各模型预报ZWD的bias、STD和RMS随高程变化情况(站点随高程升序排列)Fig.10 The bias, STD, and RMS of the forecasted ZWD from each model at RS stations sorted in ascending altitude

为检验模型精度的时间稳定性,统计了3种模型预报26个站ZWD的每日空间平均bias、STD和RMS,结果见图11。可以看到,GRNN-F-ZWD的bias绝对值在四季中大多小于GRNN-R-ZWD和GPT2w-ZWD,变化范围也明显更小,随着季节变迁没有明显的变化规律,最大绝对值小于48 mm,没有出现大的跳变,较稳定。不同季节,GRNN-F-ZWD的STD/RMS最小,振幅最小,随时间变化最平稳。所有模型的STD/RMS均在夏季出现较大值,这是因为研究区域内夏季降雨更丰富,水汽活动更活跃,ZWD变化较剧烈,因而更加难以模型化。尽管如此,基于多源数据和GRNN建模的GRNN-F模型在夏季相对其他模型仍然具有相对较高的精度,相比GPT2w,STD/RMS减小量的均值、最小值、最大值和中位数分别为12.4/14.2 mm、-6.4/-11.5 mm、44.2/43.9 mm和12.4/14.0 mm。由此说明,GRNN-F-ZWD在不同季节表现出更高的符合度。

图11 不同模型预报ZWD的每日空间平均bias、STD和RMSFig.11 The spatially averaged daily bias, STD, and RMS of the forecasted ZWD from each model at RS stations

3.3 GRNN-F计算ZWD的效率及其在PPP中的应用效果

相比如何构建模型,用户可能更关心计算ZWD的效率,因此统计了GRNN-F生成365 d、时间分辨率为5 min的单站ZWD总耗时。结果表明,生成105 120个ZWD总耗时为1 325.665 s,即计算ZWD的平均效率为0.012 6 s/个。且GRNN-F只需输入时间、坐标和GPT2w-ZWD经验值即可提前生成ZWD,可以满足GNSS实时应用的需求。

已有研究表明,将高精度ZWD约束到PPP中可以改善收敛速度和坐标高程分量的精度,在此分别将GPT2w-ZWD和GRNN-F-ZWD约束到PPP中,并对其收敛速度和U方向的精度进行比较,以验证GRNN-F应用于PPP的效果。约束策略为:使用GPT生成ZHD进行ZHD改正,然后将GPT2w-ZWD和GRNN-F-ZWD分别作为虚拟观测量约束进PPP中,具体的解算软件、策略、收敛条件及外部参考数据见表4。需要说明的是,使用GPT生成ZHD是为了避免GPT2w-ZHD和GPT2w-ZWD的自洽性。对流层延迟计算和估计不准确会使得定位精度降低,收敛时间延缓。尤其在极端天气情况下,如降雨,会导致水汽剧烈波动,使得ZWD变化更加复杂,难以准确估算对流层延迟,导致PPP收敛时间延缓。因此,选用了IGS测站JFNG站2017年DOY3(晴)、DOY86(晴)、DOY188(雨)、DOY224(雨)的观测数据,分别利用GPT2w-ZWD(方法1)和GRNN-F-ZWD(方法2)为虚拟观测量约束进行精密单点定位,来检验新模型相比GPT2w对PPP的改进效果。表5和图12给出了两种方法约束PPP的收敛时间和U方向的精度。显然,除了DOY86(晴)天有细微的劣势外,其他天GRNN-F-ZWD约束PPP的收敛时间均等于或小于GPT2w-ZWD,收敛速度平均提升了22.37%,尤其是雨天的优势更加明显。可能是由于晴天的对流层延迟变化相对平缓,GPT2w和GRNN-F预报ZWD的精度相差不大,但雨天ZWD在天气尺度的变化更加复杂,GRNN-F能较好地刻画这些天气尺度的变化,这是GPT2w等经验模型不具备的,再次证明了模型的优越性。对应的U方向精度均有提升,平均提升了37.10%,雨天的提升率更明显。总的来说,GRNN-F应用于PPP的改进效果优于GPT2w。

表4 PPP的解算策略及模型

表5 不同方法约束PPP的收敛时间和U方向的精度

4 结 论

本文联合探空ZWD、优化后的格网ERA5/GRAPES ZWD和GRNN,将机器学习引入到ZWD的建模领域,建立了相比国际典范经验模型精度更高、时空稳定性更强的ZWD预测模型(GRNN-F)。试验结果显示:①GRNN-F内符合精度bias等于0,STD/RMS均小于25 mm,拟合效果较为理想,且有很好的时空稳定性;②多源数据的引入和基于GRNN建模均有利于提高模型对ZWD的拟合精度,基于多源数据和GRNN的建模方式较主流建模方法有明显优势;③无预设模型函数的前提下,GRNN-F精度显著优于单源数据模型(GRNN-R)和通过预设模型函数表征ZWD在不同尺度上变化的模型(GPT2w),精度分别提升了11.1%和25.3%(以RS ZWD检验的RMS计),在不同时间和空间上表现出较好的预报效果和可靠性;④GRNN-F的计算效率可满足GNSS实时应用的需求,且应用于PPP的改进效果优于GPT2w。总体来说,基于多源数据和机器学习方法模型化ZWD具有明显的优越性,可为模型化ZWD提供一种思路。

致谢：感谢中国气象数据网提供的GRAPES_MESO预报数据,ECMWF提供的ERA5再分析资料,IGRA提供的探空数据。