基于耐震时程法的拱坝-地基系统易损性分析
2023-10-12姚文斌陈健云
徐 强 姚文斌 陈健云
(1.大连理工大学 海岸与近海工程国家重点实验室, 辽宁 大连 116024;2.大连理工大学 工程抗震研究所,辽宁 大连 116024)
我国水能资源丰富,尤其是西南地区,具有较高的开发利用前景.因此,我国在该区域修建了数座百米级高拱坝,在灌溉、防洪、供水、发电、航运及水产养殖等领域发挥着重要作用.但是,大坝作为主要的挡水建筑物,一旦发生破坏,将直接影响下游人民的生命和财产安全.近年来,我国唐山、汶川等地发生了烈度较高的强地震动,超过了部分建筑物的设计地震烈度,使当地的各类建筑物遭受了不同程度的破坏.地震动作为大型结构损伤破坏的重要因素,研究拱坝在地震动作用下的损伤破坏机理是有必要的.
对于特高拱坝这种大型混凝土结构,由于其结构复杂,探究坝体在不同地震动强度下的非线性响应时,需要反复进行加速度时程的调幅计算.然而这一过程十分耗时,而且计算结果可能无法收敛.为了解决这一问题,Estekanchi[1]提出了一种耐震时程法(endurance time analysis,ETA),详细阐述了耐震时程加速度曲线的合成方法,并验证了该方法在保证计算精度的同时,能有效减少计算量.白久林、杨乐等[2]基于我国的抗震反应谱,合成了ETA 时程曲线,并将其与增量动力分析方法(IDA)进行了对比,结果验证了ETA 方法的可行性.
地震的危险性分析、易损性分析和灾害损失评估是预测地震风险的3个主要方面[3].其中,易损性分析作为评估结构安全性的核心内容,近年来在研究大坝的抗震性能方面被广泛关注.大坝地震易损性分析是为了预测大坝受不同强度地震动作用时,能满足各级性能水准要求的可能性.地震易损性分析按数据资料的来源可分为经验法与解析法.经验法就是利用现有地震记录及震害资料分析易损性,解析法主要通过多组数值计算模拟地震中结构的反应.对高拱坝进行易损性分析可以发现结构在设计中存在的薄弱环节,为后期的除险加固提供依据[4-6].
国内学者曾对拱坝的地震易损性进行了研究.金爱云[7]分别采用了云分析、多条带分析(MSA)以及增量动力分析方法研究了高拱坝在地震动作用下的易损性曲线,结果表明多条带分析方法的可靠度最高;钟红等[8]考虑了多种参数的不确定性,定义了拱坝的5级极限状态,分别为无损伤、轻微损伤、中度损伤、严重损伤和破坏.姚霄雯和蒋建群[3]等考虑了拱坝的材料非线性和横缝接触非线性,分析了塑性损伤、横缝数量对拱坝动力响应的影响,以及15种地震强度指标与拱坝动力响应的相关性.最终,他们以坝顶位移和横缝开度为指标,提出了基于性能的高拱坝抗震安全评价方法.王进廷等[9]以大岗山拱坝为例,考虑材料不确定性,定义了几种极限状态,分别为轻微破坏、中等破坏和严重破坏,基于拱坝的损伤程度以及是否发生贯穿性损伤.章明旭[5]比较了直接拟合法和概率分布法用于拟合地震易损性曲线时的差异.范书立等[10-11]基于向量地震强度参数和多种工程需求参数,建立了以拱冠位移、横缝开度和损伤体积比为指标的地震易损性曲线和曲面,采用了基于响应面的方法进行了拱坝的地震易损性分析,研究结果表明响应面分析比传统的蒙特卡罗模拟法效率更高.这些研究成果为高拱坝抗震设计和评估提供了科学依据.
基于上述理论方法,本文根据水工结构设计规范[12]中的标准设计反应谱生成了20 组耐震时程加速度曲线;建立了白鹤滩拱坝-地基系统有限元模型,进行非线性时程分析,分析结构的损伤特点;选取相对位移、损伤体积比和最大横缝开度为指标,提取各指标时程,并分别基于MSA 法、回归曲线法、矩估计法及截断最大似然估计法对结构的易损性进行了分析,得出易损性曲线.通过对高拱坝进行抗震安全评价及失效概率分析,可为结构的抗震设计提供可靠依据.
1 耐震时程法
耐震时程法是一种动力推覆过程,其主要优点在于保证预测结构响应精度的同时,可以减少计算量[13-14].该方法的核心思想是生成ETA 加速度时程曲线,使得不同时间段对应的反应谱呈现既定的倍数拟合关系.
ETA 加速度时程的生成过程是先生成平稳加速度时程,然后通过反复迭代优化,使得加速度反应谱与目标反应谱的拟合程度更佳.在地震动持续时间内,不同时间段对应的目标反应谱与目标反应谱的倍数关系为:
式中:tTarget为目标时间;SaC(T)为标准设计反应谱;SaT(T,t)为目标反应谱;t为任意时间.
根据加速度反应谱与位移反应谱的对应关系可以推导出位移谱的公式为:
式中:SuT(T,t)为时刻t的目标位移反应谱.
但是,想让加速度时程上的任一时刻前对应的反应谱都能以目标谱完美拟合是不可能的,因此,可以采用式(3)对加速度时程进行无约束优化,使其对应的反应谱与目标谱更加吻合:
式中:ag为初始生成的加速度时程曲线;Tmax是地震动时长;α是位移谱的权重系数,本文只考虑加速度反应谱的影响,因此α值取0;Sa(T,t)和Su(T,t)分别为周期T下0~t时刻的加速度反应谱和位移反应谱.
基于上述理论,根据标准设计反应谱,共生成20组随机ETA 地震动时程,每组包含3条地震动时程,分别作为X、Y和Z向的动力输入.其中,X向和Y向的最大峰值加速度调幅为0.6g,Z向最大峰值加速度调幅为0.4g.图1展示了ETA 时程和IDA 时程的对比图.从图中可以观察到,ETA 时程主要具有峰值加速度不断增大的特点.分别对ETA 时程0~5 s、0~10 s、0~15 s和0~20 s各时段时程进行反应谱优化拟合,拟合效果如图2所示,可以看出,不同时段的反应谱与标准谱呈倍数关系.

图1 ETA 与IDA 加速度时程对比
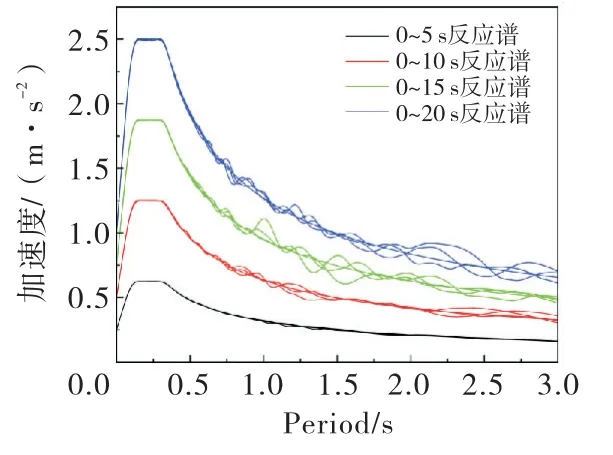
图2 ETA 时程加速度反应谱
2 结构地震易损性分析方法
结构地震易损性是指结构在某一强度地震动作用下,结构达到极限状态的概率[15],采用下式对其进行描述:
式中:F(im)为易损性概率;LS为指定的破坏指标极限状态,本文选取相对位移、最大横缝开度和损伤体积比作为破坏指标;IM为表征地震动强度的指标,本文选取峰值加速度PGA 为地震动强度指标;P[LS|IM=im]为地震动参数IM=im时,结构达到极限状态的概率.
2.1 基于回归曲线的易损性分析方法
假设地震动需求(Dd)与IM呈对数相关性,采用直线拟合lnDd与lnIM之间的关系:
式中:a、b表示回归参数;Dd表示地震动需求,也就是本文选取的损伤指标.
lnDd在每个地震动强度IM水平下,具有恒定的方差,其标准差可表示为:

2.2 基于矩估计的易损性分析方法
用含两个参数的对数正态累计分布函数来定义易损性函数,其表达式为[17]:
式中:θ为在超越概率为50%的IM水平下易损性函数的中位数;β表示lnIM的标准差.通过对任意工况下结构开始发生破坏的IM值取对数来对易损性函数的参数进行估计,其均值和标准差分别为[18]:
式中:n为工况总数量;IMi为第i个工况下结构开始发生破坏的PGA 值.
2.3 基于截断最大似然估计的易损性分析方法
最大似然估计法的原理是通过使似然函数达到最大值来对参数进行估计.通过设定所考虑的最大地震动强度IMmax,假设在进行的n次地震动分析中,有m次结构在低于IMmax的IM水平下发生破坏,通过式(12)对θ和β进行估计:
式 中:^θ和^β是 使 得 该 函 数 取 得 最 大 值 的θ和β值;IMi为第i个工况下结构开始发生破坏的PGA 值.该函数需要借助MATLAB 中的fmincon函数进行求解.将参数估计值代入式(9)中求解易损性曲线.
2.4基于多样条分析(MSA)的易损性分析方法
MSA 分析方法通过分析每一个IM水平下,损伤指标超过设定阈值的工况所占总工况比例,基于最大似然估计对参数进行估计[19]:
式中:m表示不同地震动强度的个数;xj表示逐渐增大的第j个地震动强度;zj和nj分别表示工况总数和在地震动强度为xj条件下导致结构发生破坏的工况数.式(13)的求解过程同式(12).
3 数值模拟
3.1 有限元模型
以白鹤滩拱坝为研究对象,其坝高为289 m,坝顶宽度13 m,最大坝底宽度72 m,坝顶高程为834 m,坝顶中心线弧长为709 m.坝体-地基系统有限元模型如图3所示;坝体共设有30条横缝,横缝分布如图4所示.

图3 白鹤滩拱坝-地基系统有限元模型

图4 白鹤滩拱坝横缝分布
分析中考虑的静态荷载有坝体自重和静水压力.坝体混凝土密度为2 400 kg/m3,地基密度为2 800 kg/m3.正常蓄水情况下,坝体上游静水压力水位为825 m,下游静水压力水位为604 m.坝体动水压力按照Westergaard附加质量添加,采用附加质量的形式模拟不可压缩水体对结构的动水压力.地震动采用ETA 生成的耐震加速度时程输入.
采用接触边界模型模拟混凝土拱坝的横缝,每个横缝接触面包含主面和从面,接触关系[18]如图5所示,法向接触压力的计算为:
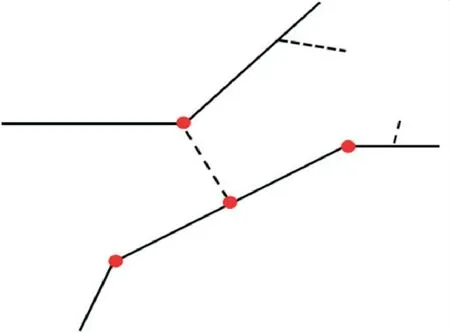
图5 主从面接触模型
式中:初始接触距离c取100 mm,初始压力p0取0.3 MPa.
为模拟地基的弹性恢复能力,采用黏弹性人工边界[20]来实现有限地基对无限地基的模拟作用,该人工边界还能吸收边界辐射能量,模拟效果良好.示意图如图6所示.人工边界上,节点上的参数由式(15)计算给出:
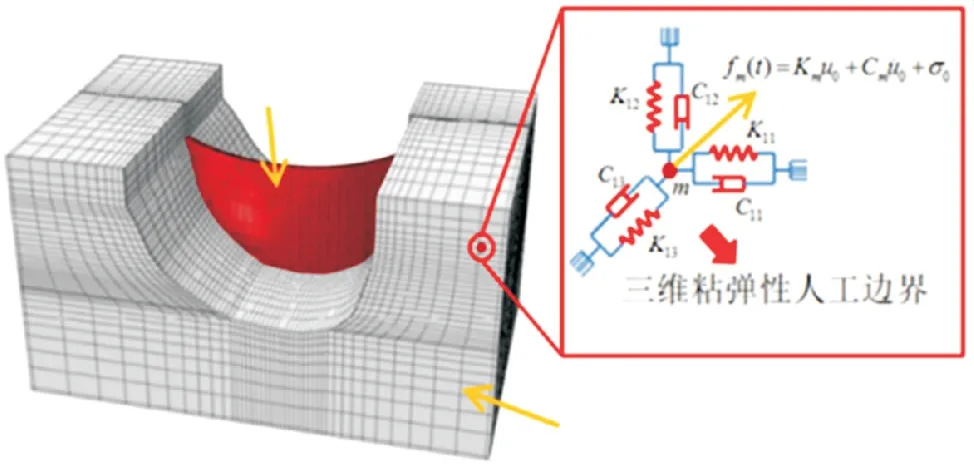
图6 黏弹性人工边界示意图
式中:Kn和Ks分别表示弹簧法向和切向的弹性刚度;Cn和Cs分别表示法向和切向的阻尼;Cp和Cs表示地震波的传播速度;ρ为地基密度;r为震源距;λ和G为拉梅常数;a和b为修正系数,a取0.8,b取1.1.
坝体混凝土材料和地基岩石的其他力学性能参数分别见表1和表2.

表1 坝体混凝土材料参数

表2 地基基本参数
3.2 动力响应分析
对白鹤滩拱坝进行动力学分析.图7展示了坝体结构在峰值加速度水平(PGA)分别为0.2g、0.4g和0.6g时,拱冠梁、下游面和上游面的拉应力损伤分布情况.从图中可以观察出,随着PGA 的增大,损伤成明显的加重趋势.在PGA 为0.2g时,只有坝踵和下游面下部存在局部轻微拉应力损伤;PGA 达到0.4g时,坝踵处损伤加重,下游面多处出现大面积损伤,但损伤值均为超过0.5,上游面损伤加重不明显;当PGA 达到0.6g时,坝踵处损伤进一步加重,下游面出现大面积严重拉应力损伤,上游面也在多处呈现不同程度损伤.拱冠梁的拉应力损伤云图也呈现明显加重的趋势.

图7 不同PGA 水平下拉应力损伤云图
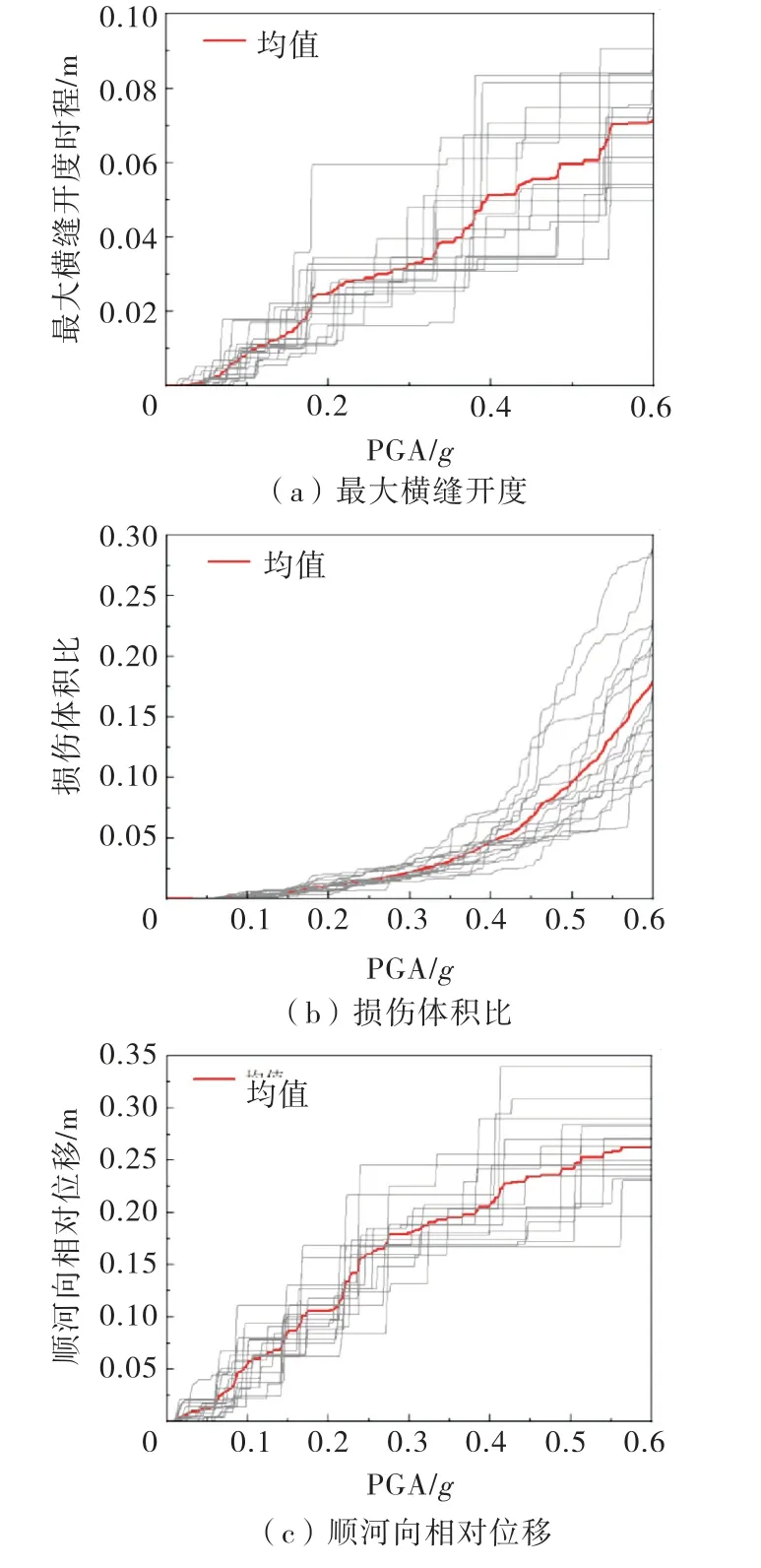
图8 各指标随PGA 的变化时程
通过对损伤云图的分析,在遭遇地震动作用时,最先被破坏的是坝踵部位,若PGA 继续增大,下游面会出现损伤,上游面需要在更大的PGA 水平地震动作用下才会出现损伤.此时,坝体在中上部出现贯穿损伤,结构存在失效风险.
3.3 损伤指标分析
采用最大横缝开度、损伤体积比和相对位移作为损伤评价指标.计算结果显示,随着PGA 值增大,各指标呈现明显的增大趋势.最大横缝开度是取各时刻30条横缝的最大开度作为该时刻的开度值.最大横缝开度随PGA 的增大平稳增长,PGA 达到0.6g时,各工况最大横缝开度最大值为9 cm,最小值约4.7 cm,平均值约为7 cm;损伤体积比[21]可以宏观地衡量损伤单元所占的比例,损伤体积在PGA 较小时增速较为平缓,但随着PGA 的增大旗增速逐渐加快,峰值加速度0.6g时,各工况损伤体积比最大值为0.28,最小值约0.09,平均值约为0.17;顺河向的相对位移是指拱冠梁底部和顶部之间的顺河向相对位移,与损伤体积比相反,在PGA 较小时增速较快,但随着PGA 的增大旗增速逐渐减缓,峰值加速度0.6g时,各工况顺河向相对位移最大值为0.34 m,最小值约0.18 m,平均值约为0.26 m.
为分析各个工况在不同PGA 水平下的离散性,分别计算了各指标在不同峰值加速度水平下的标准差,计算结果如图9所示.从图中可以观察到,标准差的整体走势是随着PGA 的增大逐渐增大.说明PGA越大,各工况离散性越高.但各指标的标准差大小和增减趋势均有所差异,PGA 在小于0.4g情况下,损伤体积比和最大横缝开度各工况的标准差较小,但在0.4g后,各工况损伤体积比标准差迅速增大.顺河向相对位移各工况标准差始终处于较高水平,说明各工况计算结果有较大差异性.
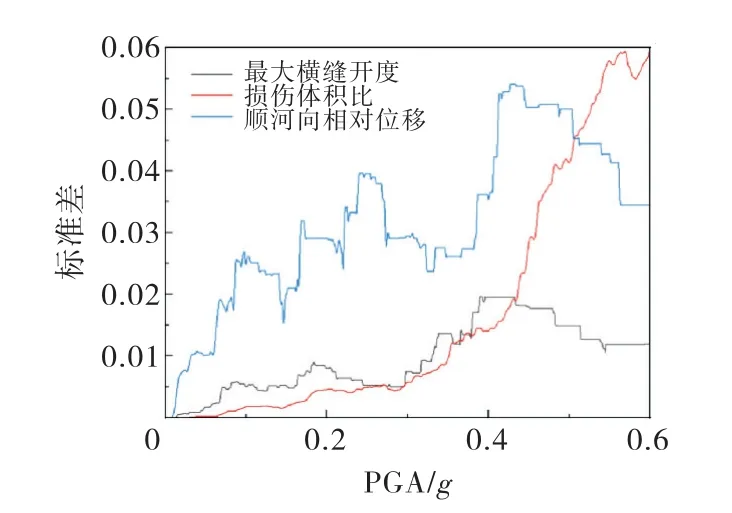
图9 各指标标准差随PGA 变化曲线
从离散性角度出发,最大横缝开度始终保持较小的标准差,更适合作为评判拱坝结构损伤破坏程度的指标.
3.4 易损性分析
本节以上文介绍的易损性分析方法,基于最大横缝开度、损伤体积比和顺河向相对位移等指标,根据以往研究成果[5,10],结合实际分析结果设定损伤阈值,对拱坝进行易损性分析,并评价了各方法与ETA方法相结合的分析效果.
3.4.1 最大横缝开度
以最大横缝开度为损伤指标,设定其损伤阈值为3 cm,分别采用截断最大似然估计法、MSA、矩估计法和回归曲线拟合法分析指标在各PGA 水平下达到该阈值的概率,计算结果如图10所示.
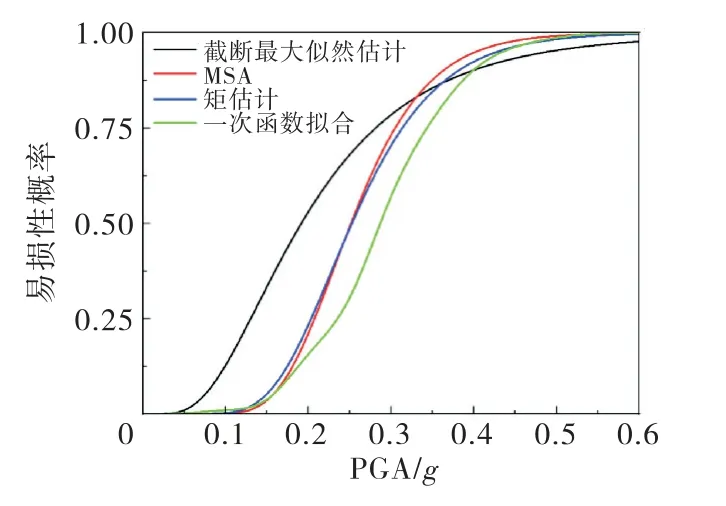
图10 以最大横缝开度为指标的易损性曲线
分析结果显示,矩估计与MSA 方法具有较高的一致性;通过截断最大似然估计计算的易损性曲线在PGA 小于0.3g时偏大,0.35g之后与其他方法计算结果较为接近;通过一次函数拟合方法计算的易损性曲线在0.2g~0.4g范围内偏小.
3.4.2 损伤体积比
以损伤体积比为损伤指标,设定其损伤阈值为0.02,通过各分析方法计算的易损性曲线如图11所示.其中,矩估计法和MSA 法依然保持了较好的一致性,一次函数拟合和截断最大似然估计法计算结果偏大.
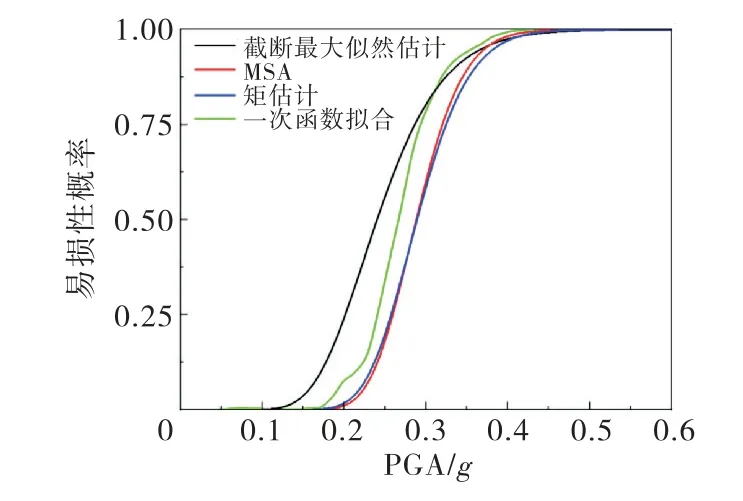
图11 以损伤体积比为指标的易损性曲线
3.4.3 顺河向相对位移
以顺河向相对位移为损伤指标,设定其损伤阈值为14 cm.易损性计算结果如图12所示.同样,矩估计和MSA 方法的计算结果高度一致,截断最大似然估计的计算结果最大,一次函数拟合方法的结果稍大,且曲线局部出现震荡现象.

图12 以顺河向相对位移为指标的易损性曲线
通过对上述3个损伤指标进行易损性分析,发现矩估计和MSA 方法可以较好地与ETA 方法相结合,对拱坝的损伤和易损性进行评估.原因是上述两种方法均依赖于给定PGA 水平下拱坝结构的响应,且给定的PGA 水平越多,曲线精度越高.本文采用的耐震时程法可以给定任意峰值加速度水平下结构的响应,因此,耐震时程法与矩估计和MSA 法相结合可以以理想的精度计算易损性曲线;虽然一次函数拟合法同样依赖于给定PGA 水平的数量,但给定更多PGA 水平下的结构响应并不能有效提高易损性曲线的精度,因此,分析结果往往有一定偏差,且曲线局部易出现震荡现象;截断最大似然估计需要预先给定地震动强度阈值,这一阈值的选取没有确定方法,且该阈值往往对易损性分析结果产生影响.
4 结 论
本文建立了白鹤滩拱坝-地基有限元模型,基于耐震时程法理论,生成了耐震时程加速度曲线,作为动力输入,作用于白鹤滩拱坝,进行动力时程分析.对多个PGA 水平下拱坝结构的拉应力损伤分布进行分析,以最大横缝开度、损伤体积比和顺河向相对位移为损伤指标,分别基于截断最大似然估计法、MSA、矩估计法和一次函数拟合法分析了拱坝的易损性,主要得出以下结论:
1)拱坝在地震动作用下的损伤破坏主要集中在坝踵和下游面中上部,随着地震动强度的不断增强,上游面出现损伤,并出现贯穿损伤.
2)标准差能反映各工况的离散性,在最大横缝开度、损伤体积比和顺河向相对位移3个损伤指标中,随着PGA 的增大,标准差均呈现增大趋势,但最大横缝开度具有相对较小的标准差,更适合作为评价指标.
3)由于计算原理不同,MSA 法和矩估计法更适合与ETA 法相结合,计算结构在不同PGA 水平下的易损性概率.
