基于递归最小二乘估算的三相逆变器无参数预测电流控制
2023-10-12严勤俞林刚汤克艰伍栋文周明
严勤, 俞林刚, 汤克艰, 伍栋文 ,周明
(1.国网江西省电力有限公司,江西 南昌 330096;2.国网江西省电力有限公司供电服务管理中心,江西 南昌 330096;3.东南大学,江苏 南京 211189)
0 引 言
有限状态集模型预测控制(finite control set model predictive control, FCS-MPC)具备快速动态响应和无调制模块等优势[1],已在高性能功率变换器广泛应用。但受模型匹配度和参数摄动等因素影响,实际应用中难以运行于最优性能[2]。围绕FCS-MPC高精度、强鲁棒预测建模问题,现有研究可分为三类:一是参数在线辨识法,文献[3]引入多模型参数辨识环节,通过在线优化移动子集实现脉冲宽度调制(pulse width modulation, PWM)整流器参数辨识,但存在搜索步长与模型参数精准辨识矛盾;二是预测误差补偿法,文献[4]提出了考虑参数不匹配和控制延时的预测误差补偿方法,有效降低预测电流误差、电流谐波,但仅可实现参数误差补偿,对未建模部分补偿能力不足;三是无模型预测控制法,文献[5]摒弃传统参数建模思路,引入无模型预测控制理念,通过在线更新各开关状态对应变化量,并用于趋势预测,但易出现“脉冲停滞”现象,造成系统性能恶化。
本文提出一种基于递归最小二乘(recursive least squares, RLS)估算的无参数预测控制方法,并基于22 kW测试系统进行验证,详细对比模型不匹配和参数摄动等条件下的运行性能。
1 传统FCS-MPC工作原理
FCS-MPC可理解为一个求解具有有限控制集的在线优化问题,预测模型作为其重要环节,准确度直接关系系统运行性能。以三相逆变器为例,简要介绍工作原理。
图1为三相逆变器电路拓扑,开关状态分别为Sa、Sb、Sc,满足
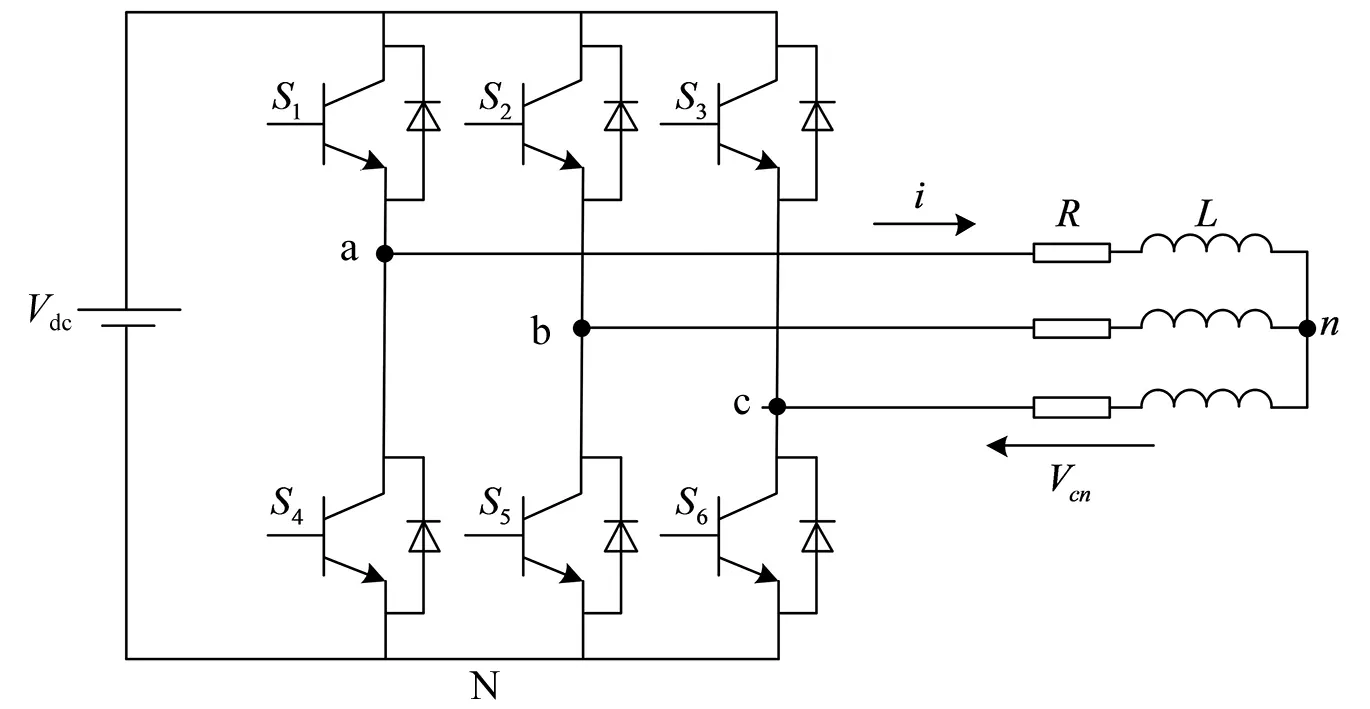
图1 三相两电平电压源型逆变器电路拓扑
(1)
式中:S为开关状态矢量;a=ejπ/3。逆变器输出电压矢量为
(2)
式中:vaN、vbN、vcN分别为逆变器a、b、c相输出电压。
逆变器电压方程为:
(3)
式中:R、L为负载电阻和电感;i为负载电流。
根据欧拉离散原理将式(3)离散化处理为:
(4)
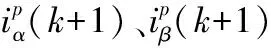
建立表征电流跟踪误差的价值函数:
(5)
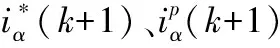
2 无参数预测电流控制方法
图2为无参数预测电流控制系统构框图,参数矩阵A、B和C为状态空间识别模块输出值,用于支撑无参数预测建模。此时,系统价值函数为:
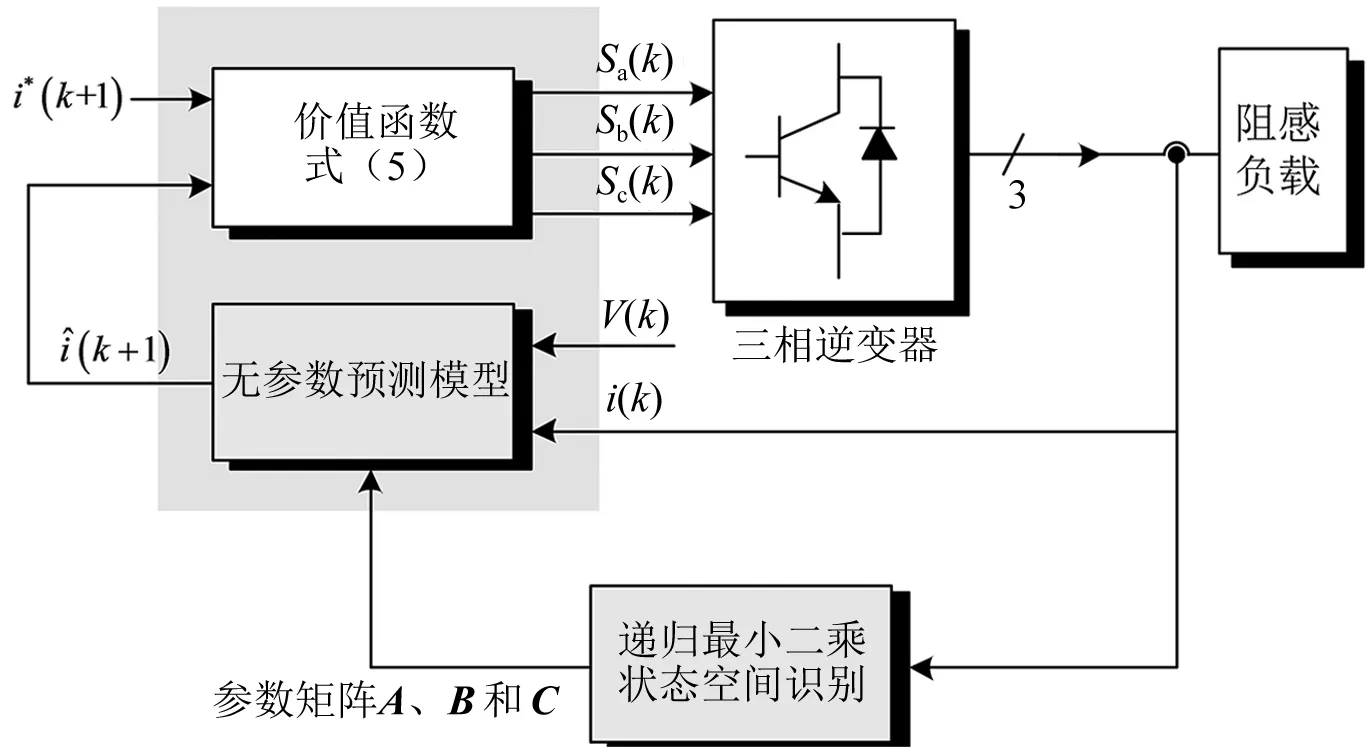
图2 无参数预测电流控制系统结构
(6)

2.1 自回归结构预测模型表征原理
将图1中滤波电感和电阻理解为先验知识未知的“黑盒系统”,控制器仅获取“黑盒系统”输入、输出变量,建立无参数预测模型。首先需确定预测模型结构和系数,本文采用ARX技术进行系统建模。
(7)
(8)
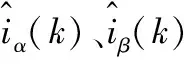
ARX模型中多项式定义为:
(9)
(10)
式中:A(z-1)的上标i为估算电流坐标系;B(z-1)的上标i、j为输入、输出坐标系;a、b为模型系数;nA、nB为模型阶数。
2.2 递归RLS估算方法
对ARX模型中需识别的未知参数采取向量表示为:
(11)
(12)
基于RLS法,利用输入、输出值进行参数估算。k时刻预测误差为
e(k)=i(k)-φT(k)θ(k-1)
(13)
式中:θ(k-1)为k-1时刻参数向量估算值;φ(k)为k时刻回归向量,满足:
φ1=[iα(k-1),…,iα(k-nA),
vα(k-1),…,vα(k-nB),
vβ(k-1),…,vβ(k-nB)]
(14)
φ2=[iβ(k-1),…,iβ(k-nA),
vα(k-1),…,vα(k-nB),
vβ(k-1),…,vβ(k-nB)]
(15)
在RLS算法中利用式(13),可将ARX模型参数更新为:
θ(k)=θ(k-1)+G(k)e(k)
(16)
(17)
(18)
式中:G(k)为增益矩阵;e(k)为估计误差;λ为遗忘因子。
图3为RLS估算算法实现流程框图。
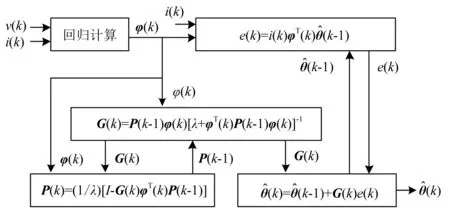
图3 RLS估算算法实现流程框图
2.3 状态空间描述和实现流程
为了便于数字处理器实现,将式(7)和式(8)中的ARX模型以观测器规范形式表示为:
(19)
(20)
至此,可将ARX系统状态空间模型整理为:
(21)
(22)
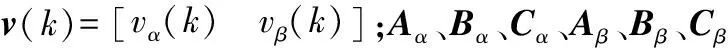
为平衡ARX模型系统描述准确度和计算复杂度,需对nA、nB系数进行必要限制,本文选择nA=3、nB=2以平衡控制性能和计算负担。至此,可确定传递函数初始形式为:
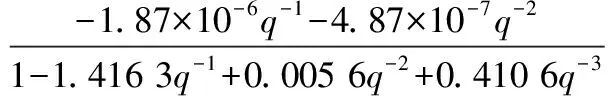
(23)
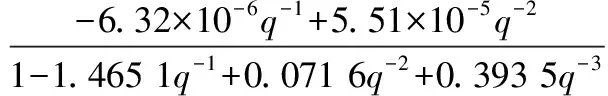
(24)
图4给出了无参数预测电流控制算法实现流程。
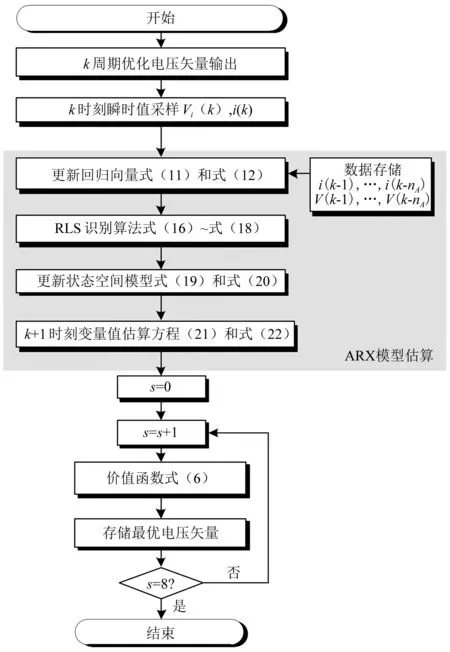
图4 无参数预测电流控制算法实现流程
3 试验验证与分析
表1为测试平台核心参数。依托该平台开展无参数模型预测控制(parameter-free model predictive control, PF-MPC)动稳态性能、参数摄动和模型失配测试,选取文献[2]所提传统FCS-MPC对比。

表1 测试平台核心参数
图5为PF-MPC动稳态性能测试结果。0.1 s电流期望值幅值|i*|由10 A阶跃至20 A,负载阻感为R=20 Ω、L=2 mH。PF-MPC无需系统模型结构和参数,可对未来状态有效预测,并在1.2 ms内快速消除跟踪误差,见图5(a)。稳态电流正弦度高,畸变率仅为4.6%,见图5(b)。综上,PF-MPC在输出电流高精度跟踪的前提下,仍具备高动态响应特征。
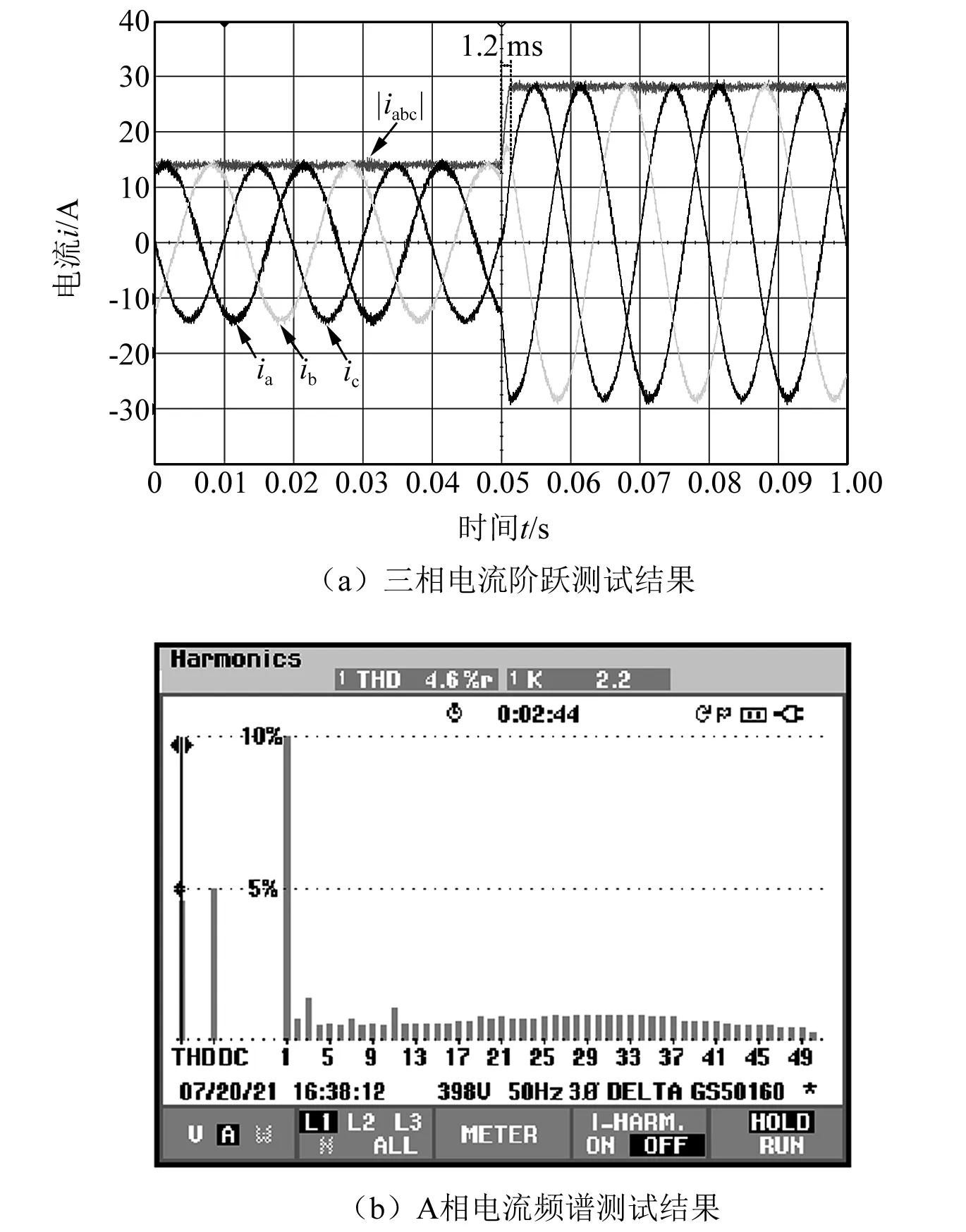
图5 动态响应性能测试结果
图6为负载参数扰动测试结果,物理系统实际负载为R=20 Ω、L=2 mH,控制系统设定参数为R=10 Ω、L=1 mH。传统FCS-MPC在参数摄动情况下性能显著下降。0.05 s后PF-MPC投入运行,可快速抑制参数扰动,在应对参数摄动问题时具备天然优势。
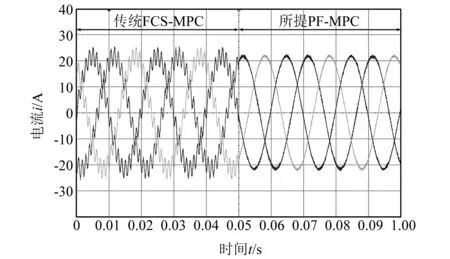
图6 参数摄动下稳态性能对比测试结果
图7为模型失配测试结果。0.05 s时刻在原电阻、电感负载上并联电容C=500 μF,传统FCS-MPC预测模型发生根本变化,系统陷入不稳定状态,见图7(a)。与之对比,PF-MPC可自适应等效模型,任保持高性能运行,见图7(b)。
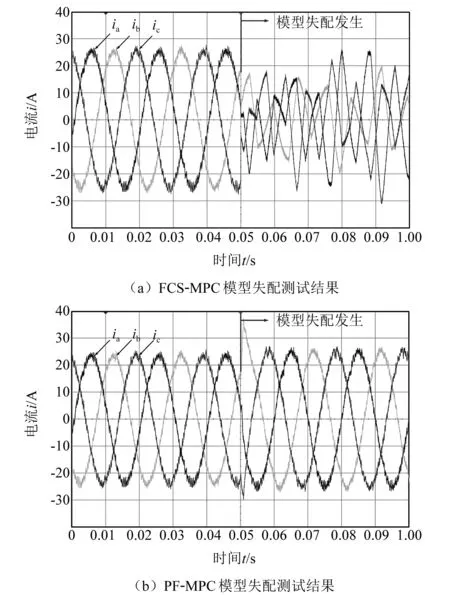
图7 模型失配下稳态性能对比测试结果
4 结束语
本文研究了一种RLS的无参数预测电流控制方法,得到以下结论。
(1) PF-MPC无需变流器物理模型和负载参数等先验知识,在应对参数摄动、模型不匹配时具备强鲁棒性。
(2) PF-MPC ARX建模仅涉及系统输入、输出数据,具备普适性,可在各类型电力电子预测控制系统推广。
