基于VMD-GRU-EC的工业用户短期负荷预测方法

蒋建香, 杨苹, 官裕达, 杨康, 刘璐瑶

(华南理工大学 广东省绿色能源技术重点实验室,广东 广州 510641)

0 引 言

在目前电力市场化改革的大背景下,大型工业用户可直接参与电力市场交易,因而对工业负荷的短期预测精度也提出了更高的要求［1］。与此同时,随着工业用户可控负荷占比增大,对工业大用户进行准确的负荷预测,可明确可控负荷的时间段和总量,进而在不影响工厂产能的基础上,暂时改变自身用电行为参与电力需求侧响应,获得电力管理平台补贴。因此,精准的用户级负荷预测能为工业用户在生产运行管理、实现需求侧响应和参与电力市场交易等各个环节提供强有力的决策支撑,使得工业用户能降低运营成本。

目前,因为用户级负荷预测的研究与系统级相比,负荷预测较少、起步较晚,常用方法有机器学习、深度学习和组合模型方法。机器学习主要通过构造出自变量和因变量的映射关系实现预测,较为常用的有支持向量机(support vector machine,SVM)［2］和随机森林(random forest,RF)［3］等方法。深度学习利用神经网络等算法挖掘数据特征,适用于非线性、容量大的数据,常用的有长短期记忆神经网络(long short term memory,LSTM)［4］和门限循环单元(gated recurrent units,GRU)［5］等。

然而,单一负荷预测模型大多存在一些不足,如鲁棒性差和适用性弱等,而组合预测模型可充分将不同算法在预测中的性能差异优势进行恰当的结合,弥补算法中存在的部分缺点。组合模型中常用的有基于数据处理和基于不同预测算法两大类。前者指的是利用算法将历史负荷数据进行处理,对处理后的数据分别搭建合适的模型进行预测;后者是基于不同预测算法的混合预测模型,即采用两种或两种以上的算法搭建模型进行负荷预测,然后通过直接叠加或增加权重分配机制将各模型的预测结果进行整合。由于组合模型的预测效果相对更好且计算机的性能足以支撑复杂模型的训练,因此逐渐成为用户级负荷预测主流方法。文献［6］借助互信息对特征变量进行排序并选取合适的输入变量集合输入基于LSTM网络搭建的预测模型,能够更好地处理波动大、随机性较强的用户负荷时间序列。文献［7］利用变分模态分解(variational mode decomposition,VMD)将负荷序列分解成不同的本征模态函数(intrinsic mode function,IMF);然后将各IMF结合气象信息构造不同的特征集输入3个模型中,将预测结果输入改进支持向量机回归(support vector regression,SVR)进行融合得到最终的预测值,对电、冷、热负荷均具有最好的预测精度。

上述预测模型在工业负荷预测中难以适应负荷的突变性,未能充分利用负荷残差序列信息进行误差修正(error correction,EC)导致负荷预测精度无法满足实际应用。因此本文提出基于VMD-GRU-EC的工业短期负荷预测方法,即将用户原始负荷数据进行清洗后,通过VMD算法将波动性、随机性较强的工业负荷分解成多个变化趋势更平稳、特征更具规律性的分量,将分量输入至GRU神经网络模型得到各分量预测值,将各分量预测值叠加重构得到初始预测值,同时采用GRU网络对残差序列进一步学习以充分利用其中的大量特征信息,得到误差预测值,将误差预测值与初始预测值相加得到最终预测值。经过实际算例仿真验证,本文所提方法能显著提高工业用户负荷预测精度,提高模型训练效率。

1 工业用户短期负荷预测模型理论基础

1.1 VMD算法

Konstantin等人在2014年提出了一个完全非递归的VMD算法,在分解过程中,VMD的目标是最小化IMF的估计带宽总［8］。因此可以用约束变分问题将其描述为:

(1)

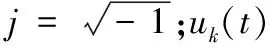
VMD求解二次优化问题的过程中选择广义Lagrange方程,在给定K值合理时,其非递归性使VMD能够有效地规避模态混叠、过分解等情况。为了便于求解式(1),需将其转化为无约束方程组。可得扩展的拉格朗日表达式如下:

(2)

式中:λ、α分别为拉格朗日乘子和二次惩罚因子。

本文选择乘法器的交替方向乘子算法(alternating direction method of multipliers,ADMM)对上式进行求解,在求解过程中不断地更新各模态分量及各自的中心频率。

1.2 GRU神经网络

GRU是对LSTM网络内部结构简化后的一种神经网络,而LSTM网络的计算原理是在继承循环神经网络(recurrent neural network,RNN)时间反馈机制的基础上,引入门控机制与记忆单元来存储和控制信息流。基于该机制建立的神经元结构具有较大的记忆容量、更强的泛化能力和自适应能力,实现信息的长时间筛选与保留,从而在一定程度上避免了RNN网络中信息丢失问题和缓解梯度的衰减速度,但LSTM神经网络内部结构更为复杂、模型训练时间较长。

GRU神经网络针对以上缺点进一步优化,在保留LSTM预测精度前提下,采用缩减门控神经网络结构参数的方式来提升模型训练效率,即GRU将LSTM三个门优化合并为更新门zt和重置门rt。GRU神经元结构如图1所示。

图1 GRU神经元结构

更新门zt用于控制结构中信息的遗忘和更新,重置门rt用于控制保留当前状态中用于计算下一状态的信息。t时刻时更新门和重置门的计算公式如下:

zt=σ(Wzxt+Uzht-1)

(3)

rt=σ(Wrxt+Urht-1)

(4)

式中:xt为记忆神经元t时刻时的输入;ht-1为记忆神经元在t-1时刻的状态;σ为sigmoid函数;Wz和Uz、Wr和Ur分别为更新门、重置门的权重系数。

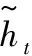
(5)

(6)

式中:Wh、Uh为隐藏单元的权重系数;tanh(·)为模拟门的功能及归一化函数。

2 基于VMD-GRU-EC的工业用户负荷预测模型

2.1 基于VMD-GRU-EC的工业用户负荷预测流程

本文的工业用户负荷预测方法包括四个阶段,依次是负荷数据分解、分量预测、预测结果叠加重构以及误差修正。图2为基于VMD-GRU-EC的工业用户负荷预测流程图。

图2 VMD-GRU-EC短期负荷预测流程图

(1) 负荷数据分解。选择VMD算法对原始负荷序列分解,得到的K个模态分量存在特征互异的特点。利用遍历法对VMD的K值从2开始分解,根据各模态的中心频率分布确定最合适的模态分量K值。

(2) 分量预测。对分解后的K个模态分量归一化处理后,根据一定比例划分训练集和测试集,对每个分量搭建基于GRU网络的预测模型,训练模型提取特征后输出各分量预测结果。

(3) 预测结构重构。将所得的模态分量的负荷预测结果均

(4) 误差修正。将残差序列归一化处理后输入至GRU神经网络中学习,得到残差序列预测值y″,最终负荷预测值y=y′+y″,并计算负荷预测评价指标。

2.2 负荷预测评价指标

(1) 效率评价指标。模型训练时间(TIME),单位为秒。

(2) 误差评价指标。为能够综合评价本文所提模型的预测效果,选取的指标有平均绝对百分误差(mean absolute percentage error,MAPE)、均方根误差(root mean square error,RMSE)和平均绝对误差(mean absolute error,MAE),三者的计算公式如下:

(7)

(8)

(9)

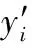
3 算例分析

3.1 数据介绍及预处理

算例中所使用的数据为某陶瓷全厂区的用电量,采集时间为2021年1月1日至2021年1月31日一年的数据,每15 min一个采样点,共2 976个数据,将前25 d的数据作为训练集,后6 d的数据作为测试集。因数据采集装置出现断电或存储故障等,会引发数据可能出现缺失、异常的状况［9］。本文选取两个临近的相似日的负荷的均值来补遗和修正数据。训练前,需对数据进行归一化处理,可以加快训练网络的收敛性。

3.2 单一预测模型对比分析

因GRU和LSTM神经网络都是常用的负荷预测算法,为验证GRU网络的预测性能,包括负荷预测的误差和模型的训练时间,设置LSTM、自回归移动平均模型(autoregressive integrated moving average,ARIMA)和SVM作为单一预测模型的对照组。LSTM和GRU的模型结构参数均采用128-64-1,即采用双隐含层结构,分别取128个和64个神经元,输出层取1个神经元。为避免偶然性,取各模型10次试验的均值作为最后的结果。负荷预测评价指标如表1所示,曲线预测结果如图3所示。

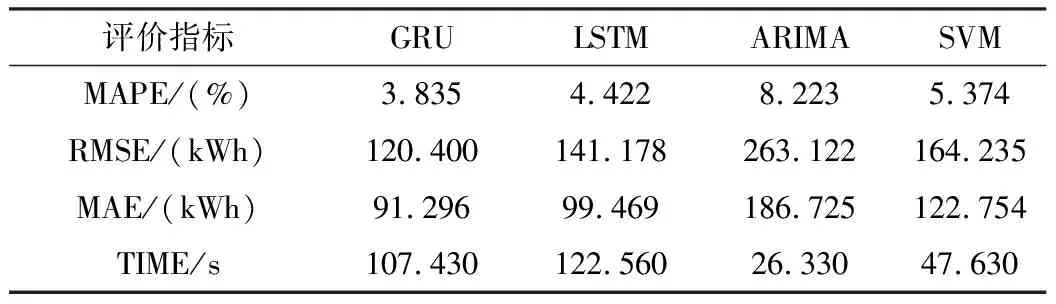
表1 各单一模型的负荷预测评价指标值

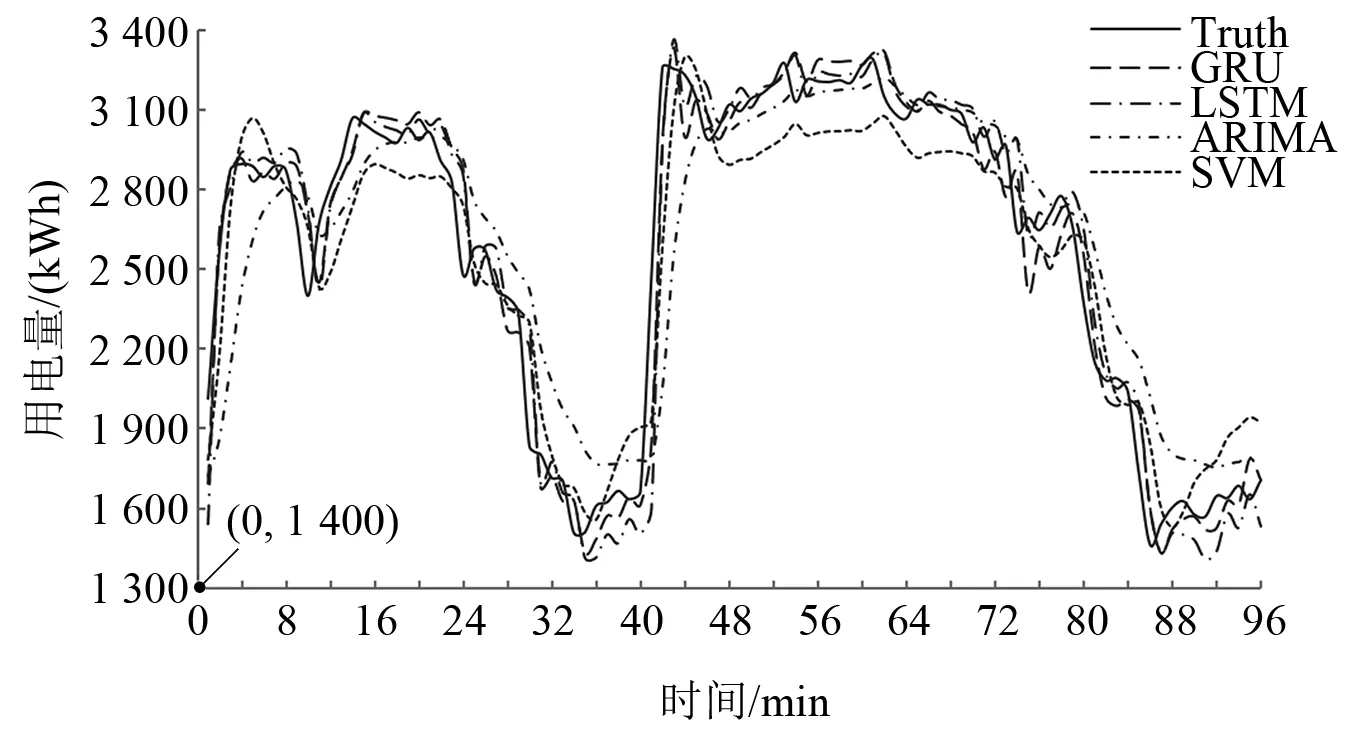
图3 不同单一模型的短期负荷曲线预测结果

从表1可知,GRU的预测误差整体略小于LSTM,但GRU的训练时间比LSTM缩短了14%,在后续组合模型中当数据被分解成多个分量需要依次预测时,可大幅降低模型的训练时间。而ARIMA和SVM两者虽然预测所需时间较短,但是预测效果较差,不适合预测负荷序列波动较大的工业用户。从图3可知,在负荷发生突变时,ARIMA和SVM的拟合程度较低,而GRU和LSTM的拟合程度更高,但是以上单一模型中负荷预测效果不佳,难以支撑工业用户在电力现货市场进行负荷曲线的准确申报。为进一步提升预测精度,本文选择基于数据分解和误差修正的组合模型完成工业用户的短期负荷预测。

3.3 组合预测模型对比分析

首先采用VMD对原始负荷数据进行分解,VMD分解的效果主要受K值的影响,不同模态的主要不同点在于中心频率的不同,因此对中心频率的分布进行观察选取合适的模态数值。表2中为不同K值下各中心频率的分布。

当新闻人的底色与这种教化碰撞，人们就可以理解“果智法师”的一些举动了。在呼吁寺庙财产公开和民主选举时，虽然充满战斗檄文的火药味，但他尽量不触及具体人名。

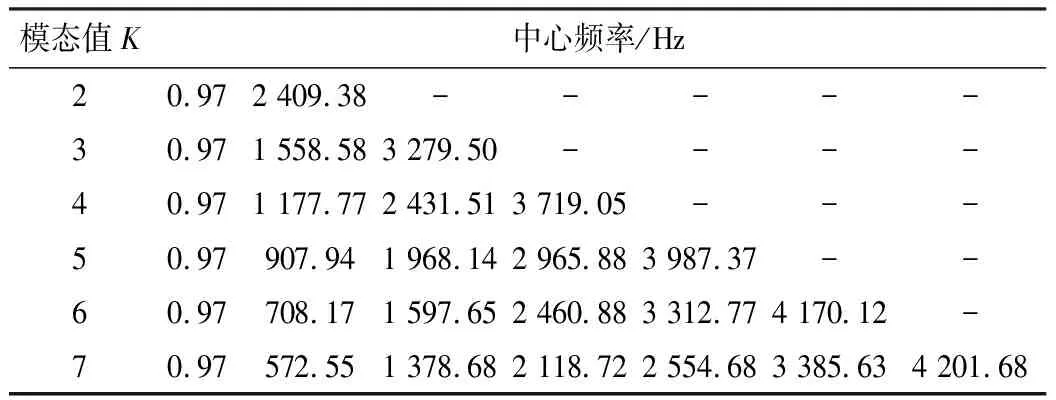
表2 不同K值对应的中心频率

K=7时分解结果中的2 118.72 Hz和2 554.68 Hz的中心频率比较接近,极有可能会发生通频带和模态混叠的情况,从而造成工业用户负荷信号的过分解,故本文的VMD算法K值取6。负荷数据通过VMD分解结果如图4所示。

从图4可以看出,VMD分解出来的高频分量幅值占比较少,有利于减少预测误差,中低频部分的分量的规律性更强,便于建模预测。负荷数据经过VMD分解后,结合LSTM和GRU神经网络来确定本文的模型以及三个对照组,即VMD-GRU-EC为本文所提模型,VMD-LSTM-EC、VMD-GRU以及VMD-LSTM三个组合预测模型为对照组。表3给出了4种组合预测模型的预测评价指标值。

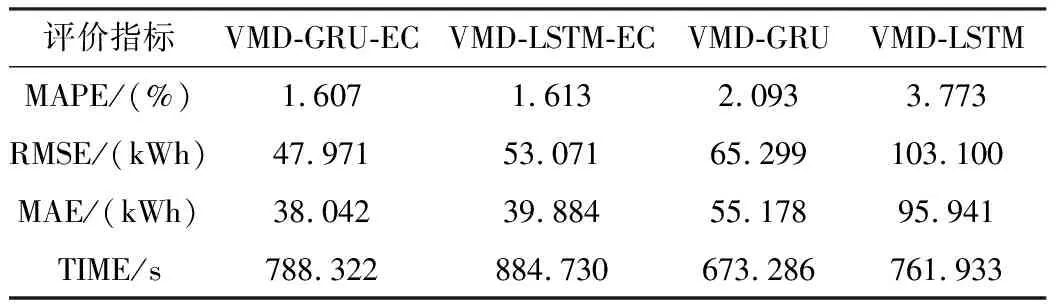
表3 各组合模型的负荷预测评价指标值

从表3可知:本文所提方法VMD-GRU-EC的误差评价指标均为最小,MAPE、RMSE和MAE比VMD-LSTM-EC分别降低了0.006%、5.1 kWh和1.842 kWh,在模型的训练时间上缩短了96.408 s,极大地提高了训练效率,特别是随着模态分量的增加,GRU的效率也会愈发明显提高。与VMD-GRU和VMD-LSTM比较可知,对初始预测值进行误差修正后,预测的精度也得到明显的提升。

从图5可知:负荷峰谷值部分VMD-GRU-EC的拟合程度最高,其次是VMD-LSTM-EC,而VMD-LSTM的拟合程度最低。故可知无论是采用LSTM还是GRU网络搭建模型,通过误差修正后,残差序列中的信息得到进一步学习,使得工业用户的负荷预测效果均得到了改善。

4 结束语

本文为解决传统负荷预测方法对负荷突变的不适性,提出了基于VMD-GRU-EC的工业用户的短期负荷预测模型。在VMD-GRU传统方法的基础上,增加基于GRU的EC部分,以弥补残差序列信息丢弃的缺点。通过算例分析的对比验证,VMD-GRU-EC相较于未进行误差修正的方法,具有对残差序列包含的信息进一步学习的优势,有效提升了负荷预测的准确率,更准确地反映工业用户的波动变化,对工业用户的生产运行、需求侧响应和电力市场的现货申报等提供一定的数据支撑。