基于VMD-BiLSTM机制的小水电日发电量预测

2023-10-12刘可真赵庆丽谭化平赵贞焰

电力科学与工程 2023年9期

刘可真，普伟，赵庆丽，谭化平，赵贞焰

（1.昆明理工大学电力工程学院，云南昆明 650500；2.中国能源建设集团云南省电力设计院，云南昆明 650051）

0 引言

受水位、流量、降雨等多种因素的影响，小水电日发电量具有较强的波动性和随机性。大量小水电接入电网增加了电力系统调度决策的复杂性，也给小水电站带来了日益突出的弃水、窝电问题[1]。对小水电日发电量进行预测可用于安排常规电源机组组合及制定日发电计划，有助于电力系统调配与运营[2]，也有助于小水电业主制定经营计划，合理地安排发电和检修时间。因此，提高小水电日发电量预测的精确度，是促进小水电开发的重要途径之一。

目前，关于小水电预测的研究主要集中在超短期的功率预测上，并取得了一定的研究成果。文献[3]提出一种结合加权马尔可夫链与灰色预测模型的两阶段预报方法。文献[4]从发电功率曲线中提取了功率变化的趋势，并提出了趋势导向的极限学习机预测模型。文献[5]提出一种基于耦合偏互信息的预测方法，实现贫资地区小水电发电能力预测。文献[6]提出一种基于改进灰狼算法优化自适应相似日选取的小水电预测方法。文献[7]提出一种基于网格化的产汇流模型和人工智能的小水电发电负荷预测方法。

针对日发电量进行预测研究已有较多成果，但主要集中在光伏和风力发电上。如文献[8]提出了一种基于粒子群算法优化Soft attention-BiLSTM机制的光伏日发电量预测方法。文献[9]提出一种基于主成分回归的光伏电站日发电量预测模型。文献[10]提出一种基于高斯混合聚类挖掘风能特征的灰狼优化算法，建立了优化长短时记忆网络参数的预测模型。文献[11]总结了目前风电中长期电量的预测技术体系和关键应用，并对未来的预测发展提出了相关建议。

光伏发电的主要影响因素包括温度、太阳辐照强度和光伏面板积尘量等[12]。这些气象因素波动性较大，导致光伏发电功率变化较大。因此，为了准确预测光伏发电量，需要以较高的采样频率（通常为15 min）进行采样，以获得更详细实时的数据来应对天气变化的影响。相比之下，小水电发电受到降雨量、水流量和季节等变化相对平稳的因素影响，发电功率较为稳定，其采集数据的频率相对较低，因此小水电预测具有更长的预测时效性。

目前，针对小水电日发电量预测的研究较为缺乏。文献[13]提出一种将非线性最小二乘算法（Levenberg marquardt，LM）和BP 神经网络（Back propagation neural network，BPNN）组合的小水电站日发电量预测方法，以预测日的前3 个连续的日发电量作为模型输入，使用LM 优化算法来优化BP 神经网络参数，最终得到当前日的日发电量预测值。文献[14]提出一种基于模糊聚类和BP 神经网络的小水电日装机利用时长预测方法，采用模糊聚类划分样本归属类别，再对每类样本采用BP 神经网络进行预测。但上述文献中，未分析小水电的日发电量特点及降雨量等相关影响因素的影响。

为此，本文提出了一种基于VMD-BiLSTM 机制的小水电日发电量预测方法。首先分析了小水电的日发电量特性和降雨量的影响；其次使用VMD 技术对日发电量数据进行分解；接着采用BiLSTM 预测工具对分解得到的各个分量单独预测，再将各分量的预测结果进行融合得到最终的预测值。最后通过算例仿真验证了本文所选模型的有效性。

1 径流式小水电日发电量特性分析

为找到适合小水电日发电量的预测方法，本文考虑先分析小水电日发电量的特性，再根据小水电日发电量的特点来选择合适的预测工具，将预测模型建立在发电规律之上，以提高预测结果的准确性。

为此，先将一段时间内的小水电日发电量数据与降雨量进行对比分析，进而得到小水电的日发电量特性。

1.1 小水电日发电量特性

图1 为某地连续3 年的小水电日发电量变化曲线。从图中可以看出，小水电日发电量整体上表现出明显的周期性，主要与季节有关：在枯水期（3—6 月），由于来水量较小，一般会安排小水电停运检修，故每年在该时段机组基本不发电；而在丰水期，来水量大，机组基本都一直处于发电状态，且日发电量较大。故小水电年运行时间一般在240 d 左右。

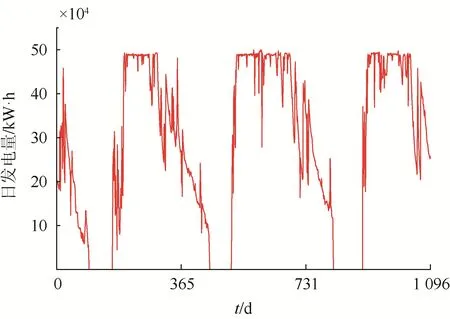
图1 某小水电连续3 年日发电量曲线Fig. 1 Daily generation curve of a small hydropower for three consecutive years

1.2 降雨量的滞后性和累积性

为了分析降雨量对小水电日发电量的影响，选取连续15 d 小水电日发电量与降雨量数据进行分析，如图2 所示。从图中可以看出，在第8 天降雨时，小水电的日发电量开始增加；在降雨量最大的第9 天，小水电的日发电量并不是最大的；在第11 天小水电的日发电量最大；在后面几日无降雨的情况下，小水电均维持在一个较大的日发电量。这表明降雨量对小水电日发电量影响存在明显的滞后性。

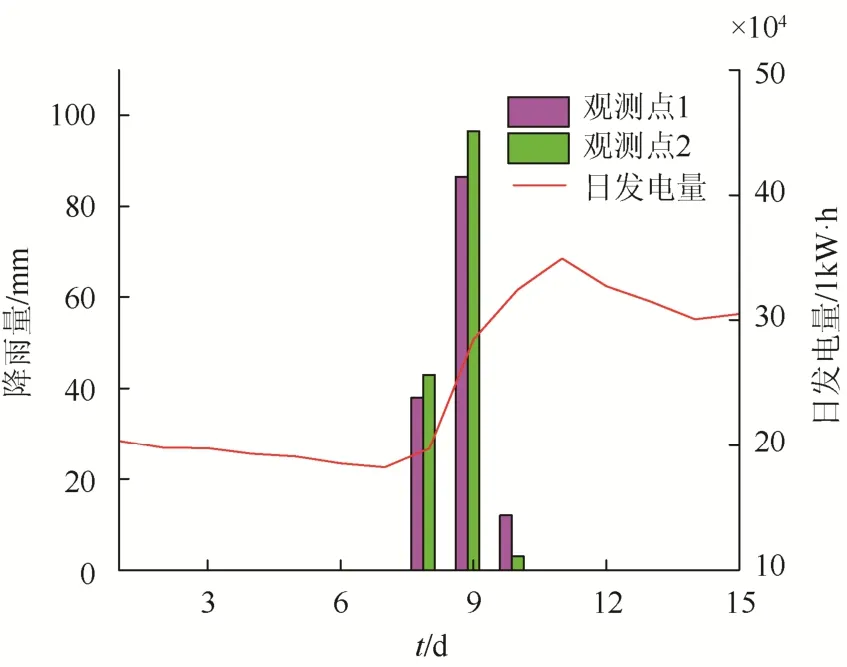
图2 连续15 d 日发电量与降雨量关系Fig. 2 Relationship between daily electricity generation and rainfall for 15 consecutive days

原因分析：小水电日发电量主要与来水量有关，而降雨量又会影响来水量。降雨后，距离河流较近的雨水会直接汇集到河流中，这部分雨水将直接导致当天小水电日发电量的直接增加；而距离河流相对较远的降雨则会先汇入地下河，再由地下河汇集到小水电上游河流，这个过程需要一定的时间，从而导致小水电日发电量存在滞后性。因此，小水电日发电量除受当天降雨量影响外，还与前几日的降雨量有关。

总之，小水电日发电量主要与所处的季节和当日及前几日的降雨量有关。

2 预测模型

2.1 数据预处理

时间序列数据收集的周期一般较长，故在收集和统计过程中难免会出现数据缺失和错误。如果在输入神经网络前不对数据进行处理，则将降低模型预测精度，或因缺失值的存在而导致训练无法进行。因此，需将输入数据进行预处理，为后续的相关性分析及模型训练奠定基础。

处理缺失值和异常值常用的方法是插补法，即根据现有的数据来推测缺失数据的值。

本文选用拉格朗日（Lagrange）插值对缺失值和异常值进行插补。假设有n+1 个互异节点x0＜x1＜···＜xn，对应函数值分别为y0,y1,···,yn，则可构造n次插值多项式Ln(x)，使得：

式中：lk(x)为 Lagrange 插值基函数；Ln(x)为Lagrange 插值多项式；j= 0,1,… ,n；k= 0, 1,… ,n。

2.2 归一化数据处理

神经网络对输入参数较为敏感。小水电日发电量数据波动幅度较大，如果直接用原数据进行训练会导致模型收敛和计算速度较慢。因此，为了提升模型训练效果和提高收敛速度，需要将输入参数归一化。本文利用min-max 归一化方法进行归一化，计算公式为：

式中：xn为归一化后的数据；xmax、xmin分别为样本数据的最大值、最小值。

2.3 VMD 分解

由于小水电的日发电量时序信号w(t)呈非线性，从整体趋势上看w(t)具有明显的周期性，而降雨量对日发电量有较大影响，因此本文考虑将日发电量时序信号w(t)进行分解，以提取信号的特征。

信号分解常被用于促进信号特征提取。用经验模态分解（Empirical mode decomposition，EMD）、集合经验模态分解（Ensemble empirical mode decomposition，EEMD）、VMD[15]等，均能将非线性、非平稳的时序信号分解为多个本征模态分量（Intrinsic mode function，IMF）[16]来提取时序信号的周期和非周期特征。相较于 EMD 和EEMD，VMD 能够有效地减少模态混叠现象，能更加有效地提取时间序列数据周期趋势特性和局部波动特征。

因此本文采用VMD 技术将小水电的日发电量时序信号w(t)分解成K个具有固定中心频率[ω1,ω2,…,ωk]的离散时间序列模态分量[u1,u2, …,uk]。

2.4 中心频率法和皮尔逊相关系数

在实现VMD 分解时需要预先确定模态数K。K值的确定对小水电日发电量的分解有较大影响。若选取K值较小，则信号将不能完全分解，信号序列中的一些重要信息会被过滤，影响分解精度；若K值较大，则信号会被过度分解，导致高频模态过多，且相邻模态分量的中心频率会过于接近，导致模态分量堆叠重复。

本文采用中心频率法和皮尔逊相关系数法来确定合适的K值。

2.4.1 中心频率法

首先设置K值（取2～6）并进行预分解。通过VMD 计算出不同K值对应的每个模态分量的中心频率分布，再对比分析，确定合适的K值。不同K值对应的中心频率如表1 所示。

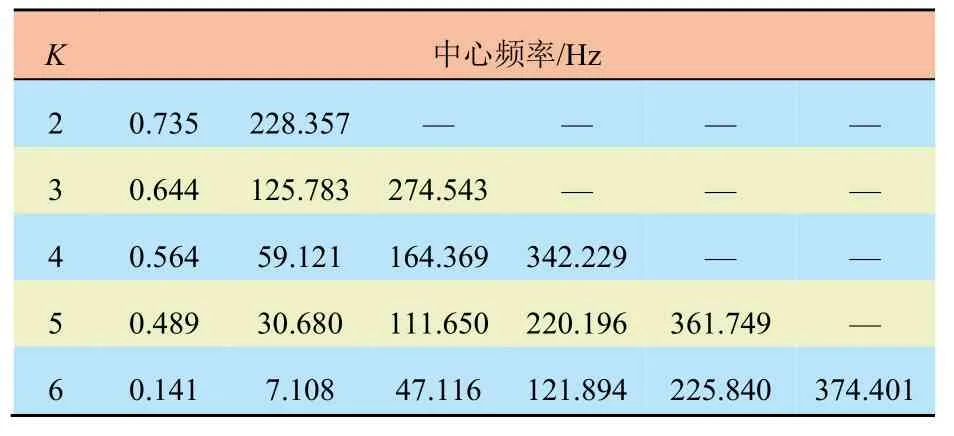
表1 不同K 值对应的中心频率Tab. 1 Centre frequencies corresponding to different values of K

由表1 可知：当K=5 时，中心频率稳定在360 Hz左右；当K=5 时，分解得到的3 个频率为111.650 Hz、220.196 Hz 和361.749 Hz 的IMF 分量之间的频率差异较小，有可能出现频带重合，进而导致分解出的模态出现混叠现象。因此本文再采用皮尔逊相关系数进一步确定最优的分解个数K。

2.4.2 皮尔逊相关系数

计算式如下：

式中：ρ(x1,x2)为x1和x2的皮尔逊相关系数；x1和2x分别为x1和x2的平均值。

设置初始分解个数K1=2。若所有相关系数均小于设定的阈值（本文设定为0.3），则取Ki+1=Ki+1进行分解，直至某次分解的Ki+1相关系数大于阈值，则确定分解个数为Ki。

ρ(x,y)取值-1～1。所得数值接近于1，表示两组变量趋于正相关的程度高；接近于-1，则表示负相关程度高；接近于0，则表示线性相关度低。

不同K值时相邻模态分量之间的皮尔逊相关系数如表2 所示。

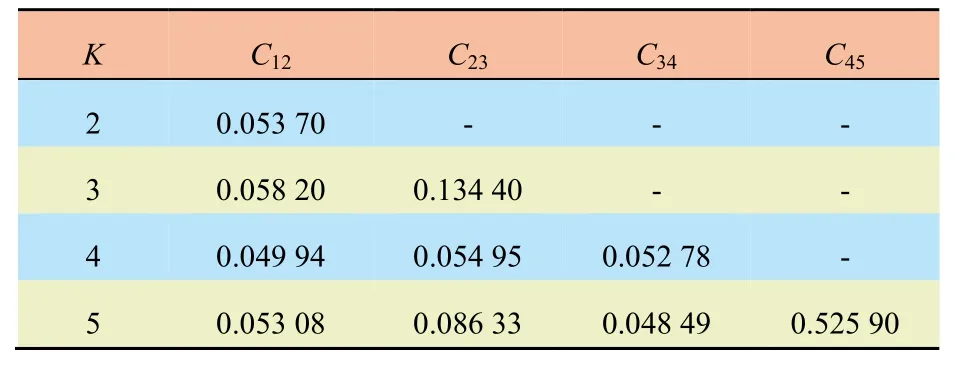
表2 不同K 值时相邻IMF 之间的皮尔逊相关系数Tab. 2 Pearson’s correlation coefficient between neighbouring IMFs at different values of K

表中Cmn表示第m个和第n个模态分量之间的相关系数。当K值小于5 时，相邻模态分量之间的相关系数均小于设定的阈值；但K值为5 时，相关系数C45为0.525 90，超过设定的阈值，表明当所选定的模态数大于等于5 时，分解成的模态分量4 和5 相关性较强，容易出现混叠现象。

结合不同K值对应的中心频率和皮尔逊相关性分析，本文选定K=4，优点是分解结果不仅能满足中心频率稳定、各模态分量之间耦合程度较低的要求，也能在保证序列分解保真度的同时避免因过度分解而造成计算效率的降低。

经VMD分解后的小水电日发电量结果如图3所示。

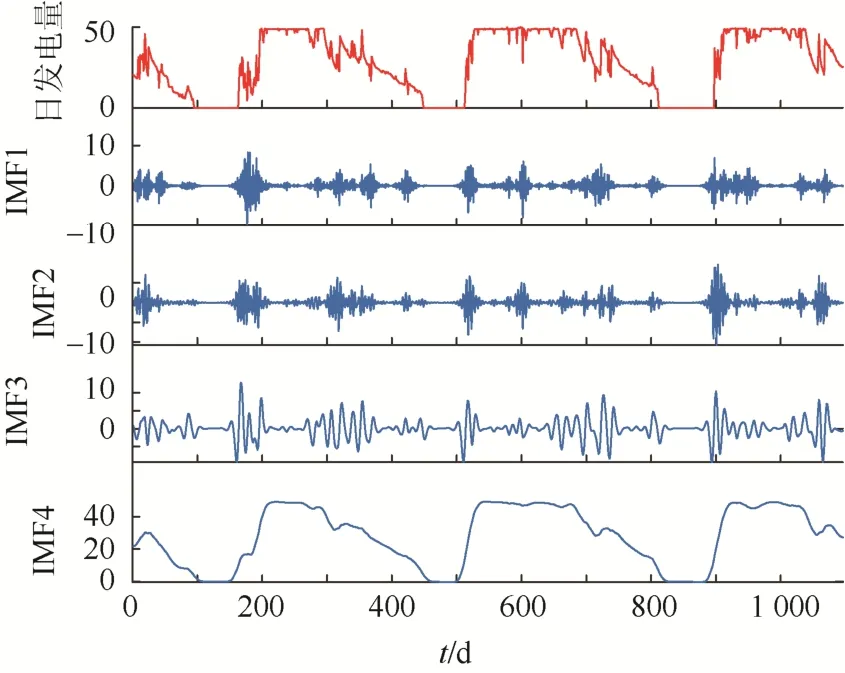
图3 VMD 分解后的小水电日发电量结果Fig. 3 Results of daily small hydropower generation after VMD decomposition

由图3 可以看到，VMD 将日发电量数据分解为不同频率下的IMF 分量。其中IMF1 和IMF2分量的频率较高，IMF3 和IMF4 频率相对较低。通过分析高频和低频成分，可以区分不同因素对发电量的影响，并更好地对日发电量进行预测。其中高频成分反映了日发电量的随机变化，而占比较高的低频成分与剩余分量则代表了具有周期性的变化和降雨量等变化相对缓慢的因素对日发电量的影响[17]，其中周期性分量可能与季节性变化或其他周期性因素有关。

2.5 双向长短期记忆网络

长短期记忆网络（Long short term memory，LSTM）是循环神经网络的一种变体，解决了常规循环神经网络因数据量过大而造成的梯度爆炸及消失的问题。相较于循环神经网络试图把所有输入信息都记住，LSTM 具备选择记忆功能，可以选择记忆重要信息，捕捉较长时间尺度的依赖关系。LSTM 的输出不仅取决于当前输入，还与之前的输入有关。

考虑到季节和降雨量对小水电日发电量带来的滞后性影响，需要捕捉小水电对降雨量及时序的依赖关系。本文采用LSTM 来预测小水电日发电量时间序列，进而提取出重要的记忆信息，以提高计算效率和计算精度。

LSTM 由遗忘门（ft）、输入门（it）、更新门（gt）、输出门（ot）组成。LSTM 结构如图4所示。

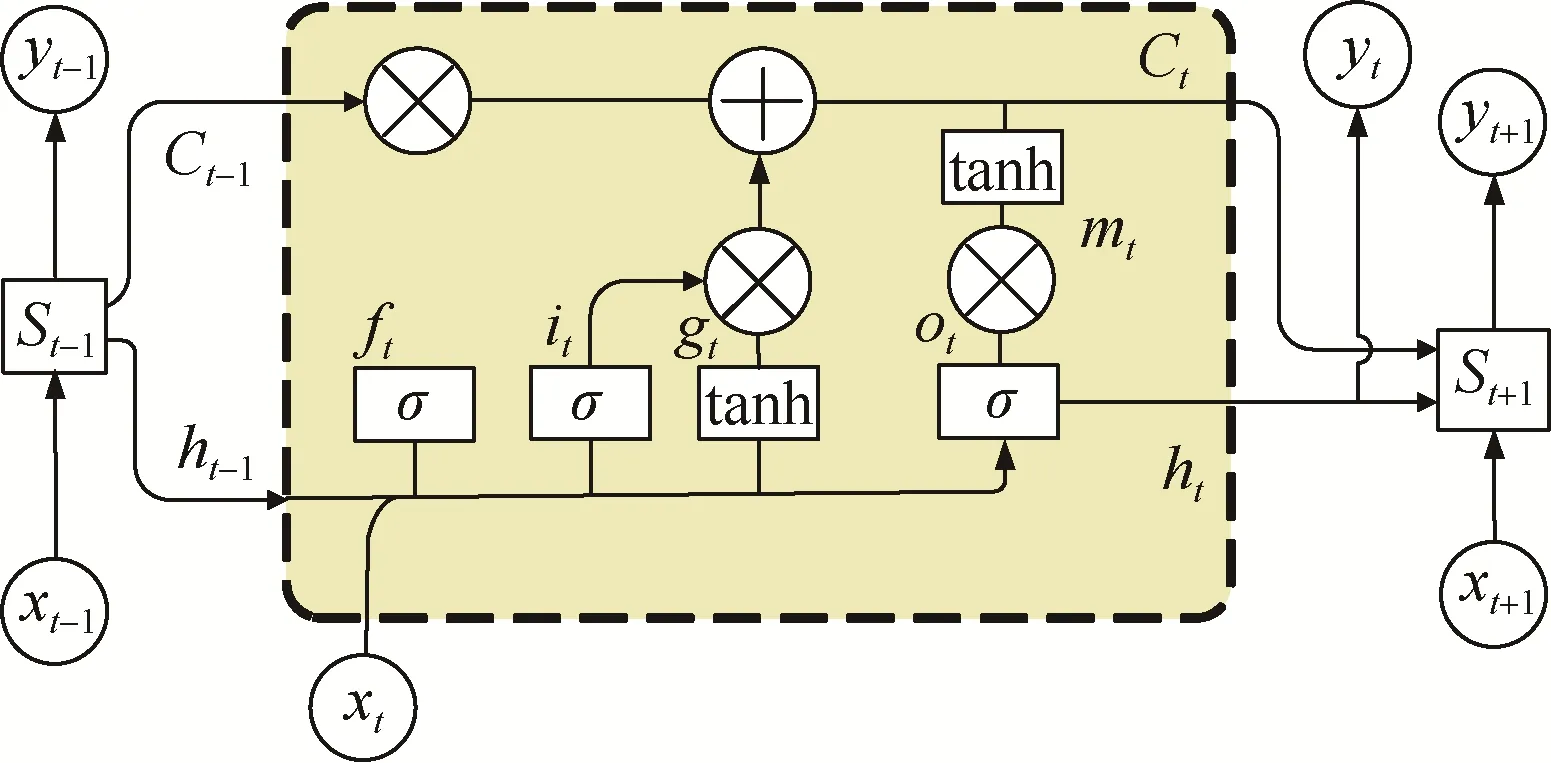
图4 LSTM 结构Fig. 4 The structure of LSTM

图4 中：ht-1和yt-1为上一时刻的输出；ht和yt为当前时刻的输出；ht+1和yt+1为下一时刻的输出；Ct-1上一时刻的细胞状态；Ct为当前时刻的细胞状态；xt为当前时刻的输入；xt-1为上一时刻的输入；xt+1为下一时刻的输入。

ft、it、gt、ot均通过权重和偏移量来控制上一时刻输出对当前输入的影响，进而控制生成的新的记忆中哪些量需要遗忘，哪些量需要保留。LSTM 计算过程包括前向传播和反向传播。

式中：σ为Sigmoid 激活函数；w和b分别为权重和偏置。

LSTM 单个神经元前向传播计算过程如图5所示。图中，ct和ht由ht-1和xt计算。

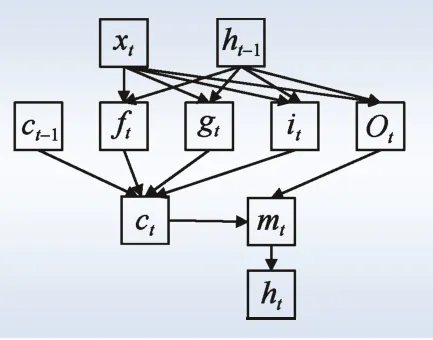
图5 LSTM 单个神经元前向传播计算过程Fig. 5 Forward propagation computational process of a single neuron of LSTM

反向传播通过梯度下降法来逐次迭代更新上述各个计算式中的w和b。

在小水电日发电量相关的历史数据中存在双向信息流[18]。LSTM 只有单向结构，只能学习到历史数据的信息，并不能考虑到未来信息的影响。BiLSTM 结合了LSTM 和双向RNN 的优点，可以同时利用过去和未来2 方向的序列信息进行模型训练，具有更强的非线性表达能力，对于同时依赖前后信息的时间序列有更好的预测效果[19]。

为此，本文选取BiLSTM 作为预测工具，以获取整个时间域内的信息，并充分学习小水电历史发电相关数据间的正反向关系。对分解出的每一个IMF 分量分别进行预测，最后再将各分量得到的预测结果进行融合进而得到最终的预测结果。

图6 示出了BiLSTM 中单个神经元的计算过程。

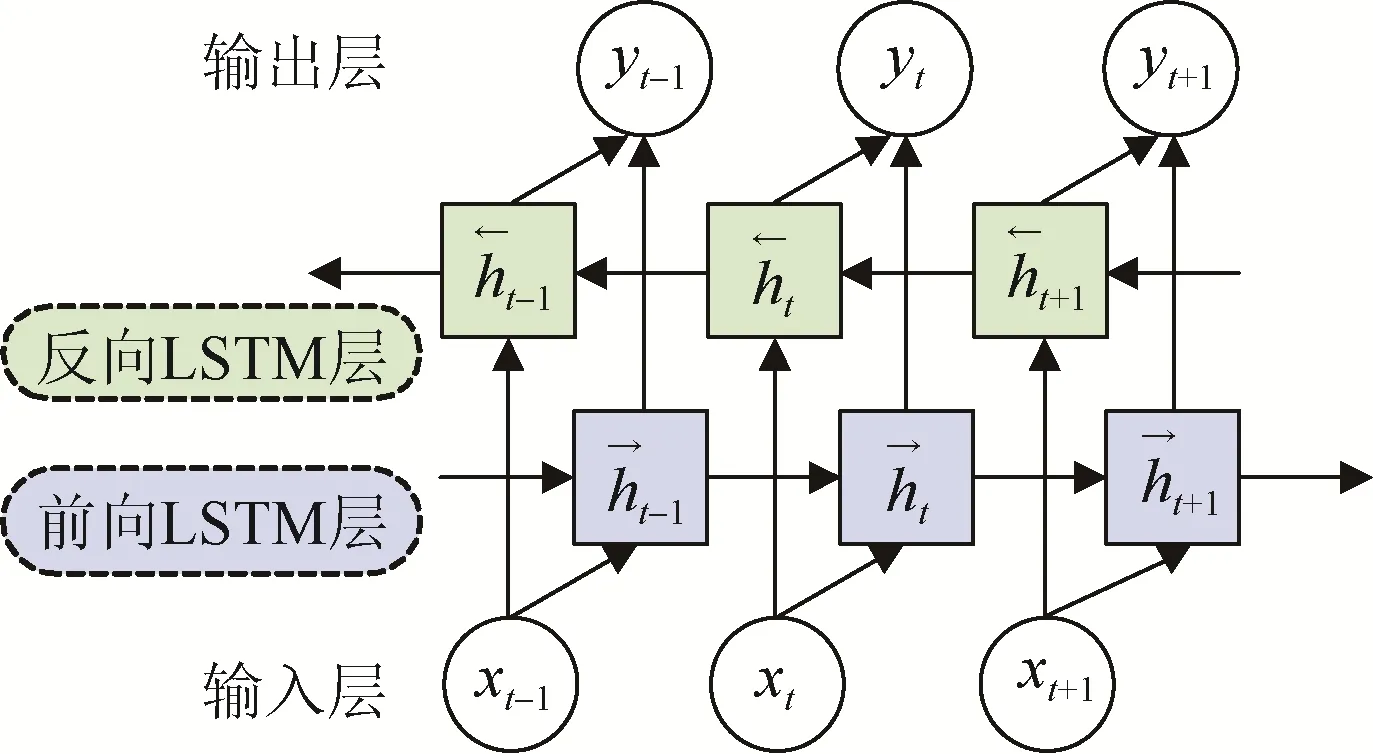
图6 BiLSTM 单个神经元的计算过程Fig. 6 The computational process of a single neuron in BiLSTM

图中，数据通过输入层进入到BiLSTM 中。前向LSTM 层将输入序列从左到右输入进行正向计算得到；反向LSTM 层将输入序列从右到左进行反向计算得到；处理完所有的时间序列后，将2个LSTM层的隐状态拼接起来，即得到BiLSTM的最终输出结果yt。计算公式如下：

2.6 反归一化数据处理

由于神经网络的输入数据是进行了归一化处理的数据，因此训练出来的数据也是归一化后的数据，故需要将预测得出的数据进行反归一化处理。反归一化处理数据实际上就是归一化数据的逆过程，只需要将归一化采用的min-max 公式进行变形即可。

3 算例仿真

3.1 数据及实验平台简介

由对小水电日发电量的特性分析可知：日发电量主要影响因素为当天和前几天的降雨量，以及所处季节。因此将小水电历史日发电量数据和周边气象站测得的降雨量数据作为预测模型的特征输入。本文采用云南某小水电站连续3 年的日发电量及周边3 个气象站监测降雨量作为实验数据。日发电量和降雨量采集时间间隔1 d，输入数据共1 096×4 个。

实验平台：11th Gen Intel(R) Core(TM) i5-11400F@ 2.60 GHz 2.59 GHz，16 GB RAM；Win11 专业版64 位，MATLAB 2020b 编程环境。

3.2 预测模型

预测流程如图7 所示。

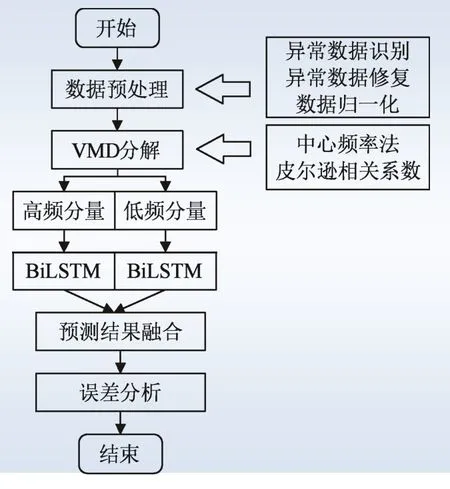
图7 预测流程Fig. 7 Forecasting process

按照8:1:1 的比例将用原始数据划分为训练集、验证集和测试集。在用BiLSTM 预测时，在可知未来气象特征的条件下，采用单步预测法计算小水电日发电量预测值，最后再根据预测值和真实值计算出模型的评价指标。

3.3 预测模型参数设置

在BiLSTM 中对各个IMF 单独预测部分。设置一层的BiLSTM，优化函数选用Adam；学习率设置为0.001；最大迭代次数为200；每次迭代使用的数据量为50，神经元个数设置为32。

为突出本文模型（VMD-BiLSTM）的预测效果，选择未考虑VMD 分解的BiLSTM 模型、LSTM模型和BP 模型进行对比。用于对比的预测模型均采用相同的输入和参数设置。

3.4 模型评价指标

为了科学地评估所选取的预测模型预测性能，需选取恰当的评估体系。在负荷预测中，短期预测评价指标主要包括：平均绝对误差（Mean absolute error，MAE）、平均绝对百分误差（Mean absolute percentage error，MAPE）、根均方误差（Root mean square error，RMSE）、拟合程度（R square，R2）等。本次预测评价指标采用MAE、RMSE、MAPE、R2，计算公式如下：

式中：n为数据量个数；yi为实际值；为预测值；为实际值对应的平均值。

评估判断标准为：MAE、MAPE、RMSE 值越小，表示误差越小，预测性能越好；R2 值越大，越接近1，模型拟合效果越好。

3.5 实验结果及分析

为减少实验的偶然性带来的影响，取10 次预测结果的平均值作为最终预测值。不同模型预测效果和相对误差分别如图8、图9 所示。

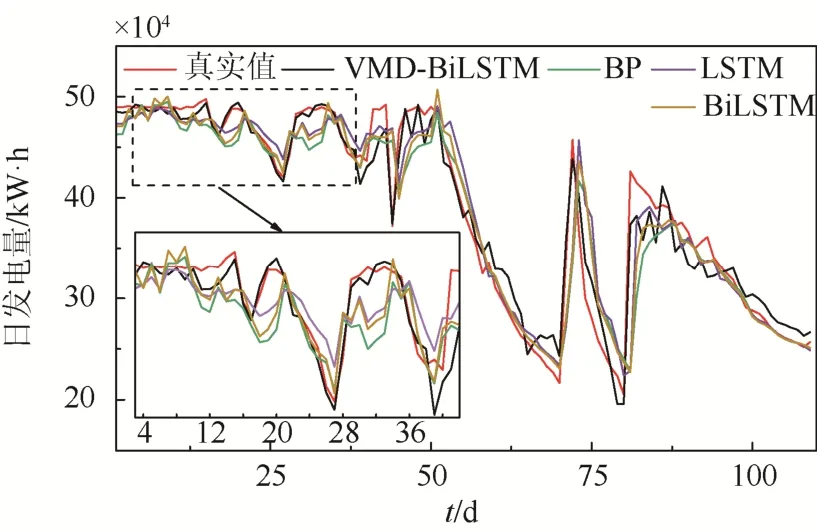
图8 不同模型预测效果对比Fig. 8 Comparison of predicted effects of different models

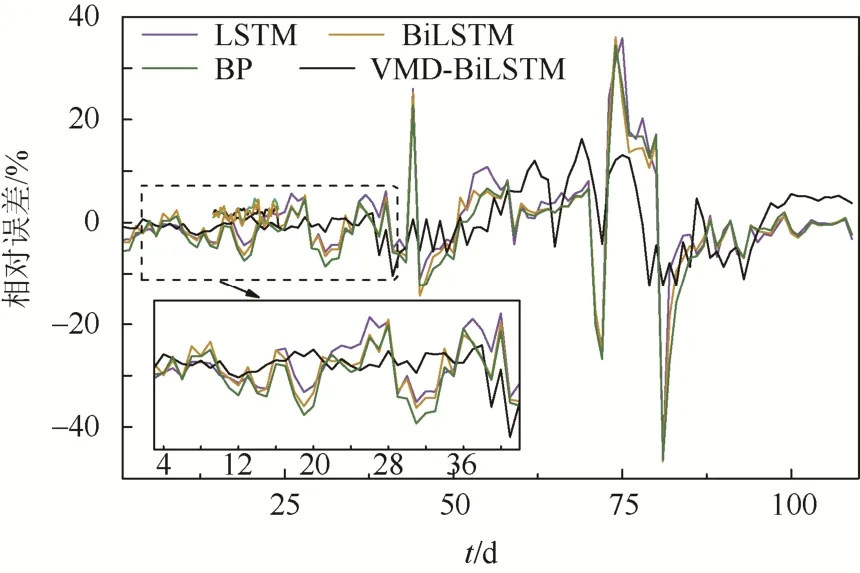
图9 不同模型预测相对误差对比Fig. 9 Comparison of relative error prediction of different models

从图8 结果中可以看到，在日发电量变化趋势相对缓慢的部分，本文所选择的VMD- BiLSTM模型预测结果基本都能够拟合小水电日的发电量变化趋势，但在日发电量变化较剧烈的部分，尤其是峰值和谷值部分，预测值与实际值偏差较大。从图9 所示相对误差对比结果来看，相较于其他模型，本文所选模型相对误差变化幅度较小，这验证了本文所选模型的有效性。

根据模型评价指标计算公式，为了观察方便，将不同模型的评价指标绘制成雷达图，最终效果如图10 所示。

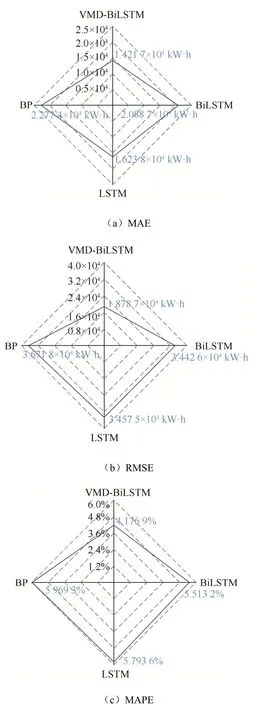
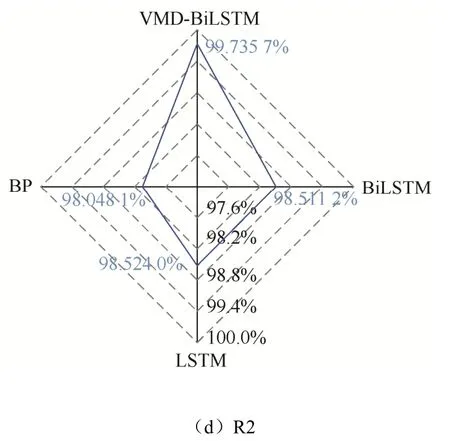
图10 不同模型评价指标雷达图Fig. 10 Radar charts of evaluation indicators for different models

从图10所示不同模型评价指标雷达图可以得出如下结论：

在算法选择方面，对比LSTM 和BP 模型，BiLSTM 模型的RMSE、MAE 和MAPE 均有所降低，但BiLSTM 模型的R2 与LSTM 相差不大。综合来看，采用BiLSTM 模型进行预测误差更低，拟合效果更佳。这也证明BiLSTM 模型能够充分学习小水电历史发电相关数据间的正反向规律，而这个特点刚好应对降雨量对小水电滞后性、累积性的影响，进而能在一定程度上提高模型预测精度。因此从预测算法选择上看，BiLSTM 更适合用于小水电日发电量的预测。

对比VMD-BiLSTM 模型和单一的BiLSTM模型，VMD-BiLSTM 模型的MAE、RMSE、MAPE均有下降，R2 有所提升。这说明在采用VMD 技术将日发电量数据分解为不同频率下的IMF 分量，对各IMF 分量分别采用BiLSTM 进行预测后，再将预测结果进行融合，这种方法能够在一定程度上提高预测精度。

此外，在训练时间方面，其余模型训练时间大约在30 s 左右，本文模型的训练时长要高于其他模型，平均在140 s 左右，属于可接受范围。由于采用VMD 分解后需将各IMF 分量分别训练K次，所以本文模型计算时长大约是单一模型的K倍。

综上所述，本文提出的VMD-BiLSTM 预测模型较BiLSTM 和LSTM 取得了更好的预测精度，能够有效提高小水电日发电量的预测性能。